Примеры решения задач
Задача 2.1.
;
;
=2/3.
Вычислить:
a)
; б)
;
в)
.
Решение. Используя свойства скалярного произведения, находим:
a)
;
б)
=
=
=
=
=3
9+4
3
4
– 4
16=
=27 –4 –64 = –61;
в)
=
=
=9+2
3
4
+16=13.
Замечание. Квадрат суммы двух векторов раскрывается по формуле, используемой в обычной алгебре.
Ответ. a) 9; б) –61; в) 13.
Задача 2.2.
;
.
Определить, при каком значении
векторы
1+
2
и
1–
2
будут
перпендикулярны.
Решение.
Из условия ортогональности двух векторов
следует, что (
1+
2)
(
1–
–
2)=0.
Таким образом,
2=
=
.
Ответ.
=
.
Задача 2.3.
Даны единичные векторы
,
и
,
удовлетворяющие условию
+
+
.
Вычислить
+
+
.
Решение.
Способ 1.
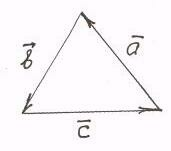
Векторы
,
,
образуют равносторонний треугольник,
у которого стороны равны 1:
;
(
^,
)=(
,^
)=(
,^
)=2
/3.
(Почему? Рис.1.16).
|
Рис. 1.16 |
Тогда
= |
+
+
=
cos(
^,
)+
cos(
,^
)+
cos(
,^
)=
.
Способ 2.
(
+
+
)2=
2+
2+
2
+2
+2
+2
=0
2+
2+
2
+2(
+
+
)=
3+2(
+
+
)=0
+
+
=
–
.
Ответ.
+
+
=
–
.
Задача 2.4. Даны
векторы
={4,–2,–4}
и
={6,–3,2}.
Вычислить:
а)
; д)
пр
;
б) (2
–3
)(
+2
);e)
пр
;
в) (
–
)2; ж)
направляющие косинусы вектора
;
г)
; з)
пр
.
Решение. Векторы и заданы координатами в ортонормированном базисе, поэтому:
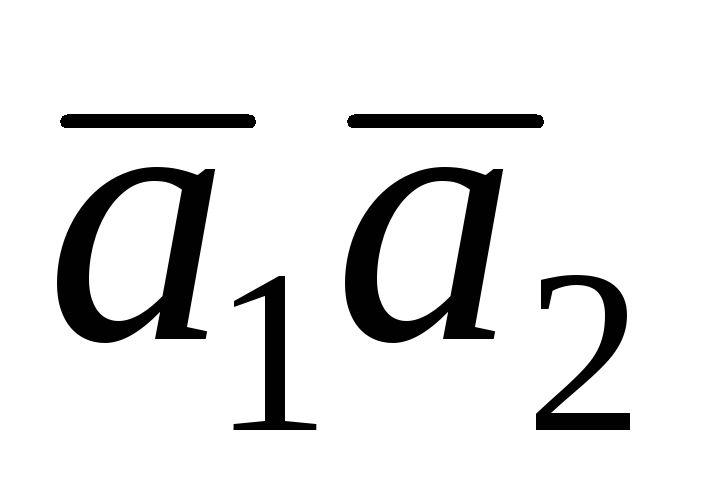= 4
6
+ (–2)
(–3)
+ (–4)
2
= 24+6 – 8 = 22.
б) Способ
1.
.
Способ 2.
2
={8,–4,–8};
3
={18,–9,–6};
={–10,5,–14}.
Аналогично
;
=–10
16+5
(–8)–14
0=
–200.
в)
=36–2
22+49=41.
г) Координаты
вектора
={2,–1,–10},
тогда
=
=
.
д) пр
=
=
=
.
е) пр
=
=
.
ж) Для решения этой
задачи вспомним формулы для направляющих
косинусов вектора
{x,y,z}:
,
,
.
Замечание.
{cos
,
cos
,
cos
}=
–
орт. вектора
.
В нашем случае
=
=6
и таким образом cos
=
=
,
cos
=
=
–
,
cos
= –
=
–
.
з) Пр
=
=
–
.
Ответ.
а) 22; в) 41; д)
; ж)
cos
=
,
cos
=
–
,
cos
=
–
;
б) – 200; г) 105; е)
;
з) –
.
Задача 2.5.
Найти единичный вектор, имеющий
противоположное вектору
направление, если
={6,–2,–3}.
Решение.
Орт вектора
,
,
,
так как
=
=7,
то
.
Полученный вектор
,
поэтому искомым вектором является
.
Ответ.
.
Задача 2.6.
Вектор
,
коллинеарный вектору
={6;–8;–7,5},
образует острый угол с осьюOz.
Зная, что
=50,
найти его координаты.
Решение.
Способ 1. Так
как вектор
коллинеарен вектору
,
то
.
Зная, что
=50,
получаем
=50,
откуда
12,5
=50
=
4.
Вектор
образует с осьюOz
острый угол, следовательно, аппликата
z
у него должна быть положительной, т.е.
=
–4. Таким образом,
={–24;32;30}.
Способ 2.
Так как вектор
коллинеарен вектору
,
то
=
,
следовательно,
.
Вектор
образует с осьюOz
тупой угол (так как его аппликата
),
следовательно,
0,
т.е.
=
–
=
–4,
={–24;32;30}.
Ответ.
={–24;32;30}.
Задача 2.7.
Найти вектор
,
зная, что он перпендикулярен векторам
={2;3;–1}
и
={1;–2;3}
и удовлетворяет условию
(2
)=
–
6.
Решение.
Пусть
={x,y,z},
тогда из условия ортогональности вектора
к
и
следует, что
,
.
Известно также, что скалярное произведение
вектора искомого вектора на данный:
.
Таким образом, получаем систему трех
линейных уравнений с тремя неизвестнымиx,
y,
z:
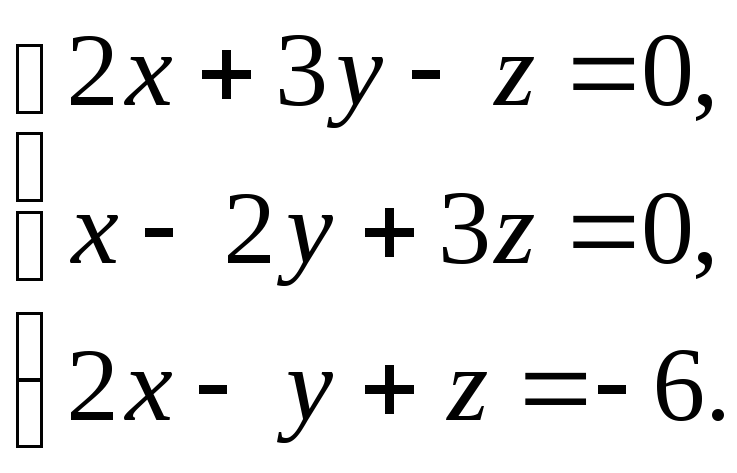
Решая систему,
получаем
,
,
,
т.е.,
={–3;3;3}.
Ответ.
={–3;3;3}.
Задача 2.8.
Вычислить работу силы
=
при перемещении материальной точки из
положения А(–1,2,0)
в положение В(2,1,3).
Решение.
Найдем координаты вектора
,
вдоль которого перемещается точка
приложения силы:
={2–(–1);1–2;3–0}={3;–1;3};
=
(
–
вектор пути). Работа силы
на пути
равна скалярному произведению векторов
и
.
Так как
={1;2;1},
то А=
=
.
Ответ. 4 ед. работы.
З
адача
2.9. Даны
вершины треугольника А(3,2,–3),
B(5,1,–1),
C(1,–2,1).
Определить его внешний угол при вершине
А.
B
Решение.
=(
^
)
(рис. 1.17).
={5–3,1–2,–1–(–3)}={2;–1;2};
={2;4;–4}.
A
C
cos
=
=
=
Рис. 1.17
=
=
;
.
Ответ.
.