Свойства определителя

Ниже перечислим свойства определителя.

1. Определитель не меняется при транспонировании

=.

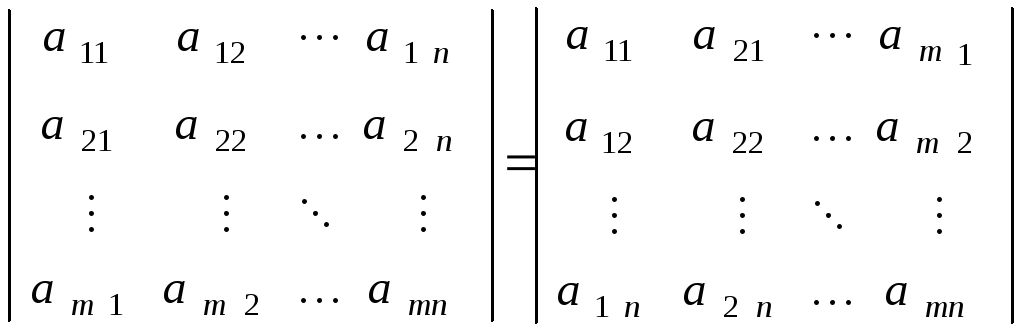Это означает, что строки и столбцы определителя равноправны.

Из этого свойства вытекает, что определитель матрицы равен определителю транспонированной матрицы .

Например,

=.

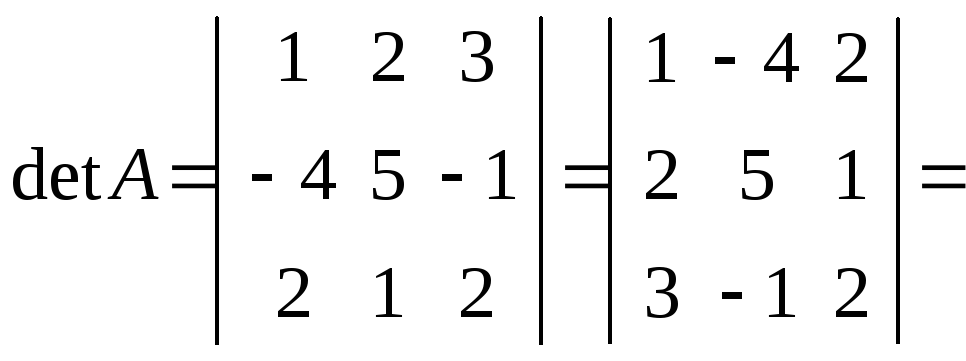
2. Если одна из строк или один из столбцов определителя состоит из нулей, то определитель равен нулю

Например,

=.

3. При перестановке двух строк или двух столбцов определитель меняет только знак.

Например,

detA=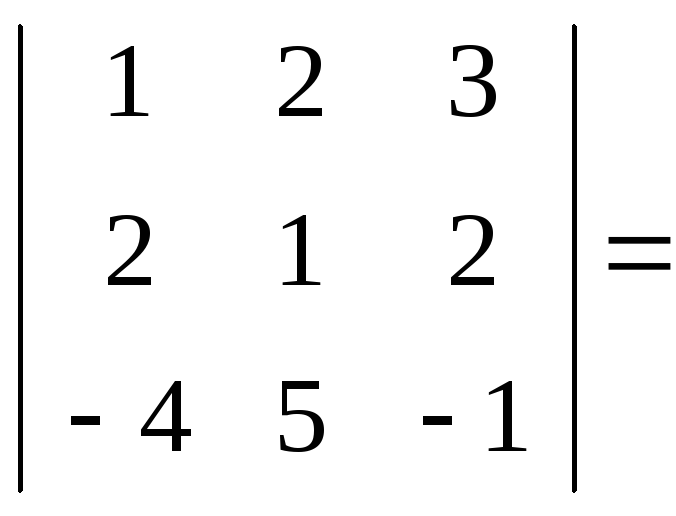

4. Определитель, содержащий две одинаковые строки или два одинаковых столбца, равен нулю.

Например,

5. Если все элементы некоторой строки или некоторого столбца определителя умножить на число k  0, то сам определитель умножится на это число.

Иначе это свойство можно сформулировать так: общий множитель всех элементов некоторой строки или некоторого столбца можно вынести за знак определителя.

Например,

detA=.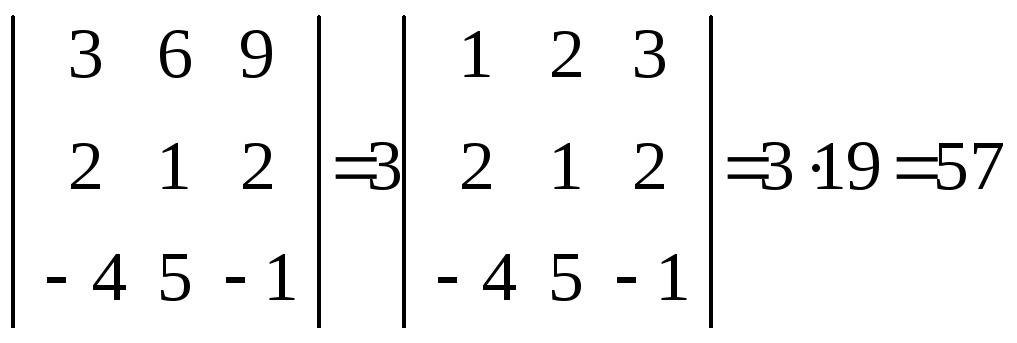

6. Определитель, содержащий две пропорциональные строки, равен нулю.

Например,

7. Если все элементы i-й строки определителя n-го порядка представлены в виде суммы двух слагаемых; то данный определитель равен сумме двух определителей, у которых все строки, кромеi-й, такие же, как и в заданном определителе, a i-я строка в одном из слагаемых состоит из элементов b_ij , а в другом - из элементов c_ij, то есть

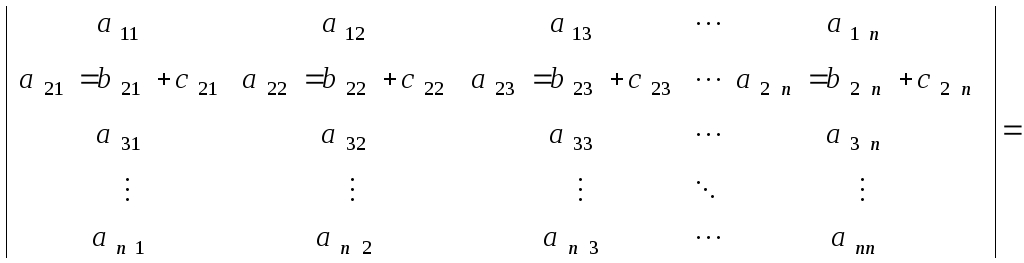
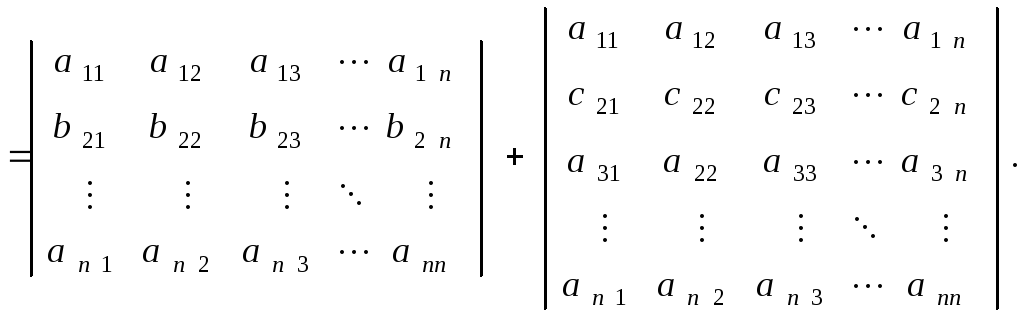
Например,

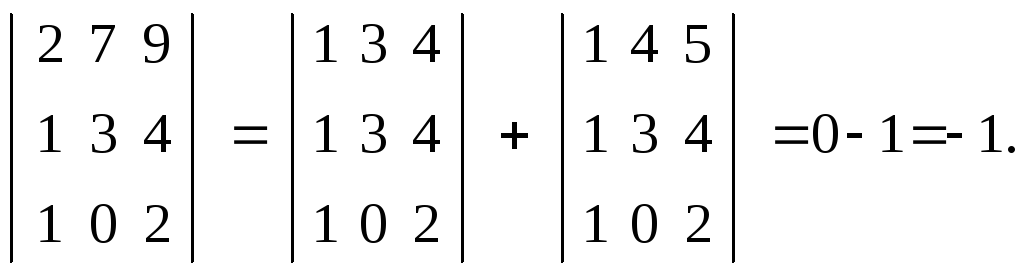
8. Если одна из строк определителя представляет сумму каких-либо других строк или сумму произведений каких-либо других строк определителя на число k, то определитель равен нулю.

Например,

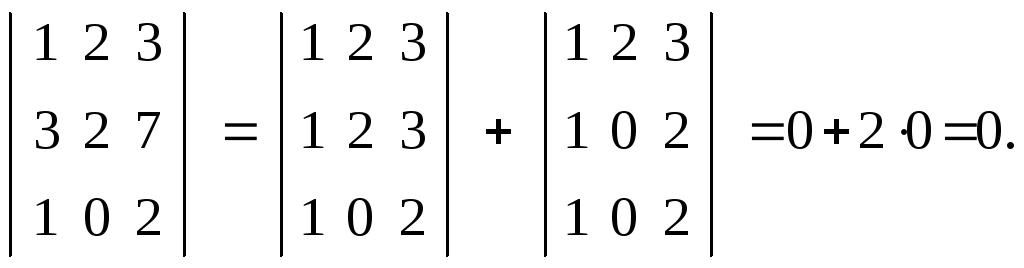
9. Определитель не изменится, если к элементам одной строки из его строк (столбцов) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Например,

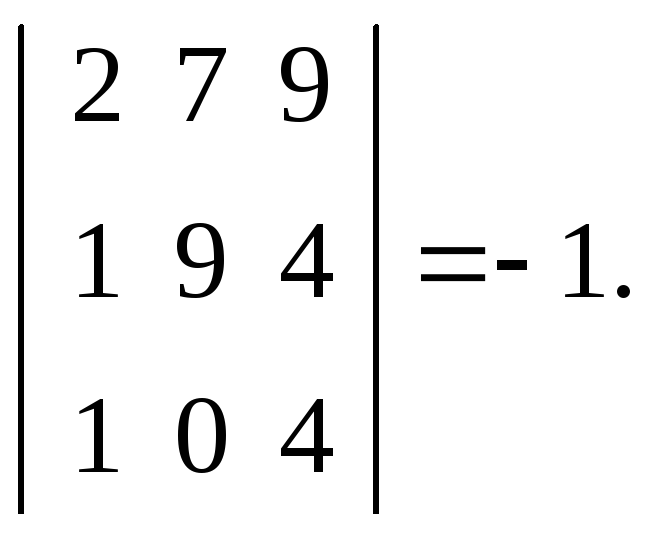
Умножим третью строку на 3 и прибавим ко второй строке, тогда:

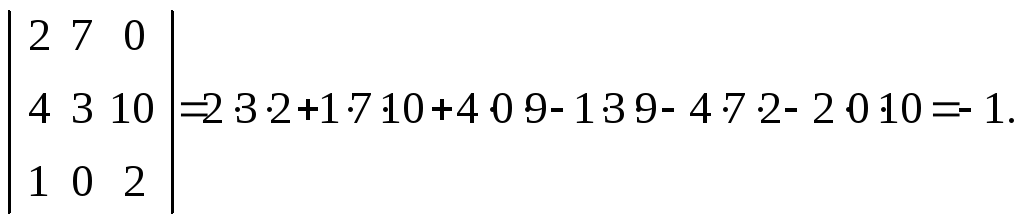
Преобразования, не изменяющие величину определителя называются элементарными.

В заключение этого раздела отметим, что для вычисления определителя п-го порядка нужно вычислить выражение, состоящее из п! членов. Так, если порядок определителя равен 10, то он равен выражению состоящему из 10! членов. Количество арифметических действий для вычисления определителя порядка n равно nn!. При n=10 необходимо выполнить арифметическое действие равное 10 10! Что является очень громоздкой и трудоемкой операцией.

§3. Обратная матрица

определение 1. Матрица А называется невырожденной (неособенной), если ее определитель не равен нулю, и вырожденной (особенной) в противном случае.

Перечислим некоторые свойства таких матриц:

а) произведение двух невырожденных матриц размерности иесть невырожденная матрица размера;

б) произведение любой невырожденной матрицы и вырожденной квадратной, той же размерности, есть вырожденная матрица.

OПРЕДЕЛЕНИЕ 2. Квадратная матрица называется обратной по отношению к данной невырожденной квадратной матрице, если ее умножение как справа, так и слева на данную матрицу дает единичную матрицу.

Для матрицы A обратная обозначается через A^–1 . По определению обратной матрицы имеем

(1)

OПРЕДЕЛЕНИЕ 3. Матрица называется союзной (присоединенной) для A, если

.

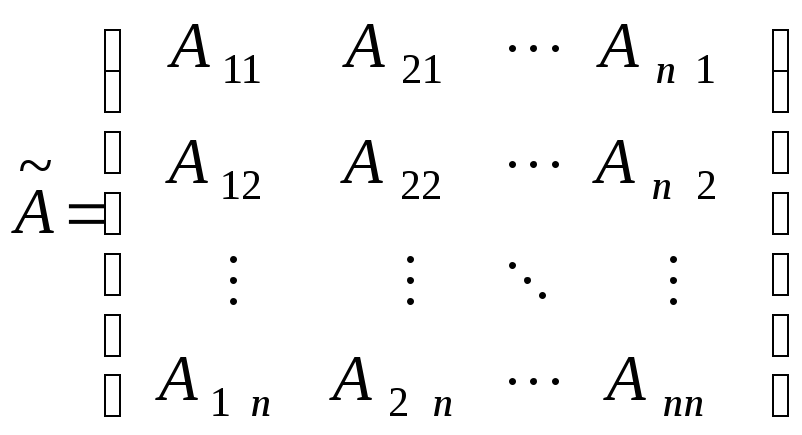где A_ij алгебраические дополнения элементов а_ij определителя A.

CВОЙСТВО ПРИСОЕДИНЕННОЙ МАТРИЦЫ .Рассмотрим произведение матрицы A на матрицу.Имеем

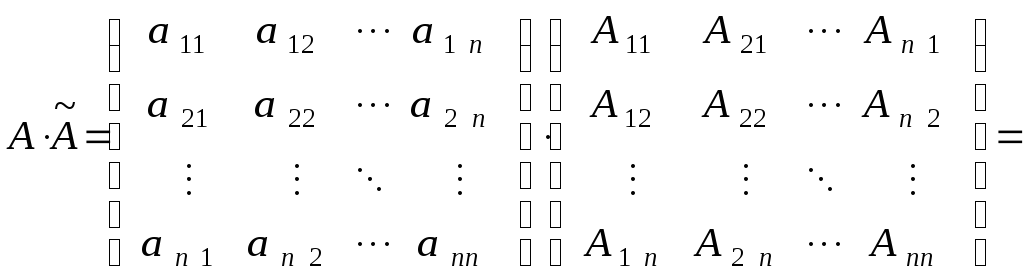
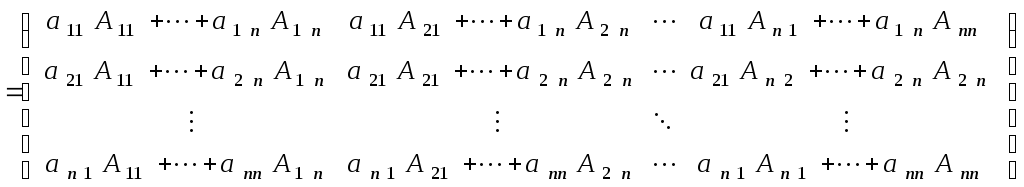
Диагональные элементы полученной матрицы есть сумма произведений элементов строки определителя на свои алгебраические дополнения . Поэтому все диагональные элементы полученной матрицы равны ,а внедиагональные элементы этой матрицы равны нулю, так как каждый внедиагональный элемент равен сумме произведений элементов строки определителя на алгебраические дополнения элементов другой строки.

Таким образом,

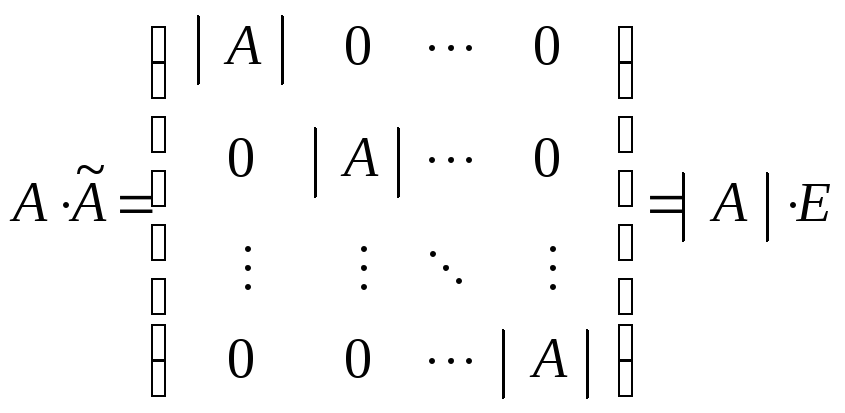(2)

оПРЕДЕЛЕНИЕ 4. Матрица A^T размером называется транспонированной по отношению к матрице A размером если для всехi и j, кроме i = j.

Итак, в соответствие с определением , если в матрице

размером заменить строки соответствующими столбцами, то получится матрица

размером , которая называется транспонированной по отношению к матрице A.

ПРИМЕР. Найти A^T для матрицы A, где

.

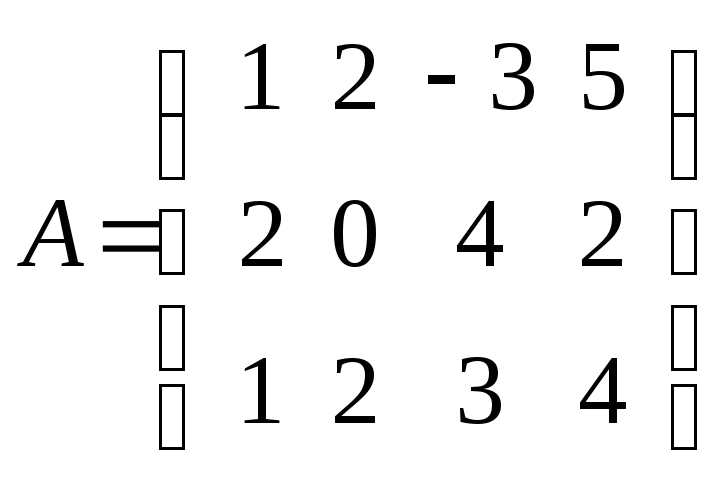Для матрицы

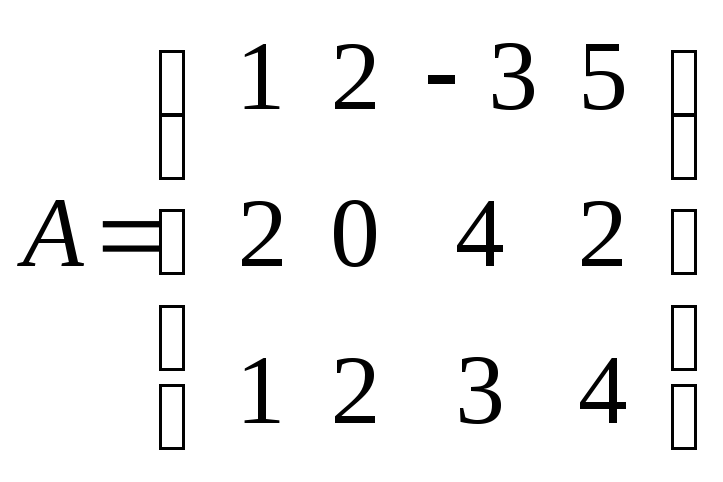
размером 34 транспонированной является матрица

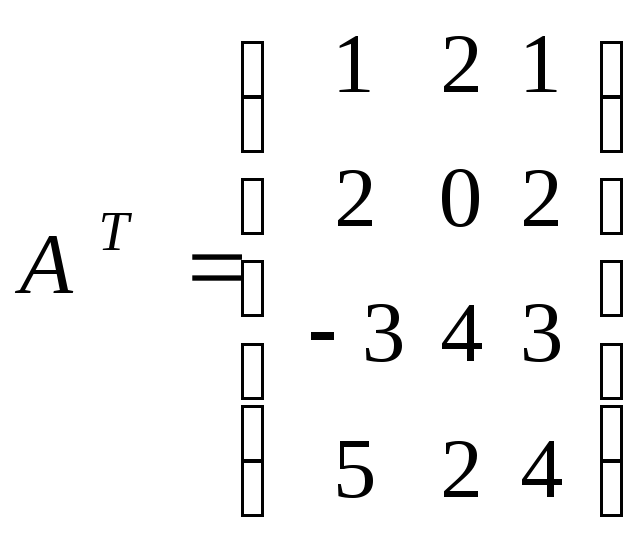
размером 43.

Имеют место соотношения:

а) , б),

в) , г)

Т е о р е м а. Для того, чтобы квадратная матрица A имела обратную A^-1 необходимо и достаточно, чтобы определитель матрицы A был отличен от нуля, то есть, чтобы матрица A была неособенной.

Необходимость.

Пусть для матрицы A существует обратная A^-1, тогда

Откуда

,

то есть матрица A невырожденная.

Достаточность. Предположим, что матрица A - невырожденная, то есть0. Построим присоединенную матрицу для матрицыA.

Тогда

(3)

то есть для матрицы A существует обратная.

Теперь рассмотрим процесс обращения неособенной квадратной матрицы

n -го порядка

A=,

то есть нахождения A^-1.

Для этого сначала находим значение . Далее составляем матрицу, элементами которой являются алгебраические дополнения элементов определителя, соответствующего данной матрице. Затем транспонируем ее и, в итоге, полученная матрица является союзной по отношению к исходной матрице.

Далее в соответствие с формулой (3) , получим

. (4)

Пример. Найти A^-1 для матрицы

.

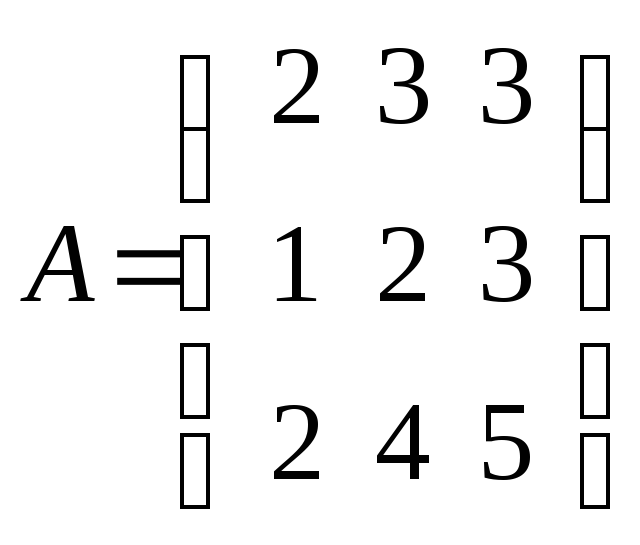Сначала вычисляем данной матрицы A. Имеем .

.

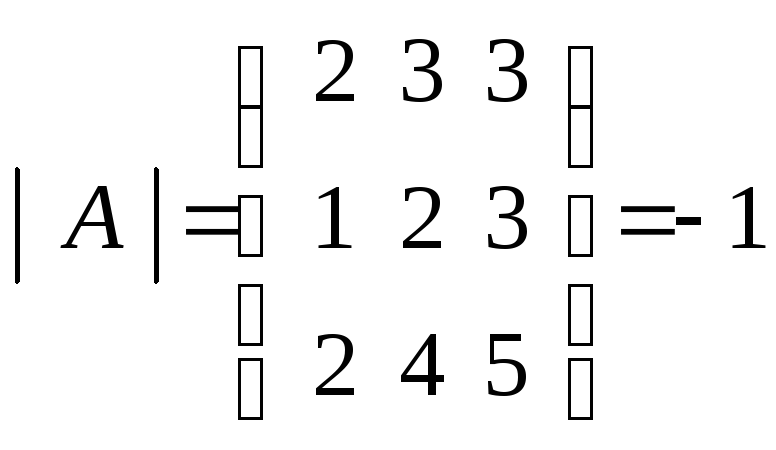Затем составляем союзную матрицу . Для этого находим алгебраические дополнения для всех элементов определителя исходной матрицыA.

Получаем:

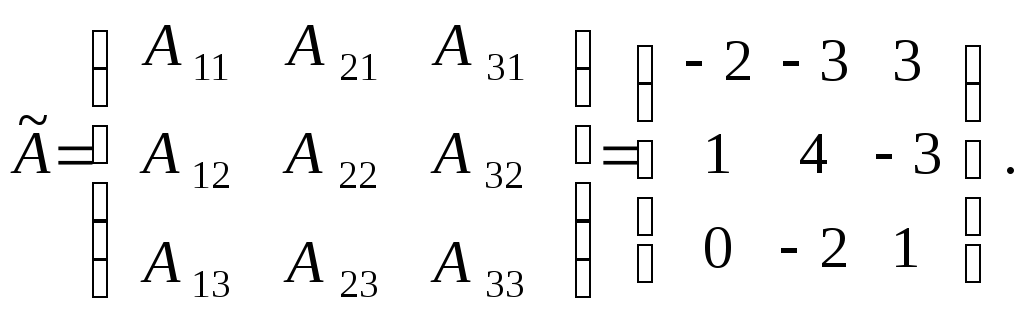
Далее вычисляем обратную матрицу

.
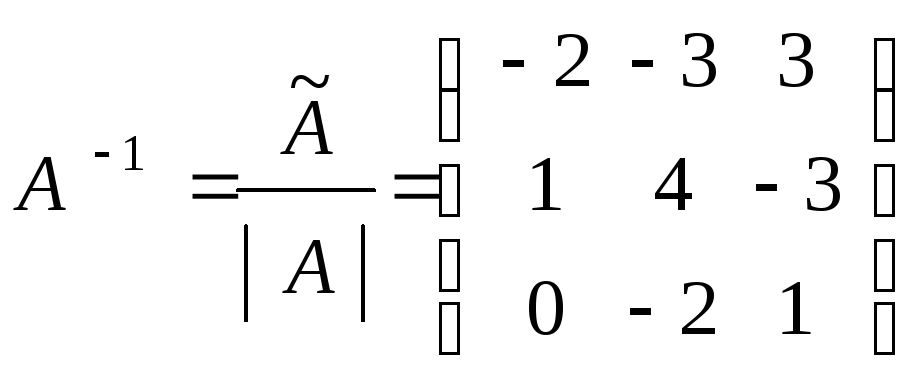