УП Основы эконометрики

∑n (yi − a −αx2i − (1 −α)x3i )2 → min .

i=1

Непосредственное дифференцирование приводит к уравнениям, из которых эти оценки могут быть найдены:

naˆ +αˆ ∑(x2i − x3i )= ∑(yi − x3i )

aˆ∑(x2i − x3i )+αˆ ∑(x2i − x3i )2 = ∑(yi − x3i )(x2i − x3i ).

Однако может быть выведена и общая формула, позволяющая учесть линейные ограничения [4].

Если в процессе подгонки модели учитываются линейные связи между параметрами, то оценки регрессии получаются более эффективными. Если до этого имела место проблема мультиколлинеарности, то она может быть смягчена. Даже если эта проблема в исходной модели отсутствовала, то выигрыш в эффективности может дать улучшение точности оценок, так как в этом случае уменьшаются значения их стандартных ошибок.

Пример 3.3. [5]. Производственная функция Кобба-Дугласа, рассчитанная для производственного сектора США за 1899-1922 гг. выглядела без учета линейного ограничения на параметры как (в скобках указаны стандартные ошибки):

Оценки параметров α и β в модели без ограничения действительно

в сумме дают примерно единицу, что может служить обоснованием для использования ограничения, учет которого повышает эффективность оценивания (сравните значения стандартных ошибок).

Вопросы для самопроверки и упражнения

4.1.Что такое полная коллинеарность и мультиколлинеарность факторов? Перечислите характерные признаки мультиколлинеарности.

4.2.Какие из перечисленных факторов учитываются в регрессии с помощью фиктивных переменных: 1) профессия, 2) курс доллара, 3) численность населения, 4) размер среднемесячных потребительских расходов, 5) местоположение пункта продажи?

4.3.С помощью фиктивных переменных напишите уравнение, соот-

ветстующее наличию двух структурных изменений в моменты времени t0

и t1 , t0 <t1 .

71

4.4.Предположим, что вы оцениваете регрессионную зависимость расходов на мороженое от располагаемого личного дохода, используя наблюдения по месяцам. Объясните, как вы введете фиктивные переменные для оценки сезонных колебаний? Какую интерпретацию дадите коэффициентам регрессии? Какие гипотезы сможете протестировать?

4.5.Рассчитайте парные и частные коэффициенты корреляции для данных примера 3.1. Сделайте вывод о наличии или отсутствии в модели мультиколлинеарности факторов.

4.6.Почему введение линейных ограничений на параметры модели приводит к увеличению точности их оценок?

72

Глава 5. Обобщенная линейная модель множественной регрессии

При моделировании многих реальных экономических или социальноэкономических процессов естественно возникают ситуации, в которых условия классической линейной модели множественной регрессии оказываются нарушенными. Так, если в качестве исходных статистических данных используются временные ряды или пространственно-временные выборки, то , как правило, условия некоррелированности и гомоскедастичности случайных ошибок (или регрессионных остатков) не выполняются, становятся нереалистичными. Использование обычного МНК в таких случаях будет давать плохие результаты, так как МНК-оценки неизвестных параметров модели не всегда будут несмещенными и эффективными. В этой главе мы обсудим некоторые обобщения многомерной регрессии и методы, при использовании которых можно получить лучшие результаты.

Классическая регрессионная схема может быть обобщена в соответствии с тем, какие из условий этой схемы могут быть нарушены. И здесь можно выделить два направления такого обобщения. Во-первых, это отказ от предположения, что независимые переменные или регрессоры являются неслучайными, т. е. детерминированными величинами. В экономической практике часто это предположение оказывается нереалистичным. Обычно обнаруживается, что объясняющие переменные модели сами были определены из других экономических зависимостей. И потому при проведении анализа их следует рассматривать как случайные величины или, как принято определять, стохастические регрессоры. Оказывается, что при выполнении некоторых естественных условий (например, некоррелированности матрицы регрессоров X и вектора ошибок ε ) МНК-оценка вектора неизвестных параметров сохраняет основные свойства МНК-оценки в стандартной модели. Другим методом оценивания, который позволяет получать оценки с более приемлемыми свойствами в случае стохастических регрессоров, является метод, основанный на инструментальных переменных [4,5,8,9]. Подробное изложение этого вопроса выходит за рамки данного пособия.

Второе направление в обобщении многомерной регрессии связано с изучением линейной модели, в которой ковариационная матрица вектора

ошибок ε , обозначим ее через Ω, не обязательно имеет вид σ 2 In , а мо-

жет быть произвольной симметричной положительно определенной матрицей (это случай, когда ошибки коррелированы и имеют различные дисперсии). С помощью линейного преобразования исходную систему можно свести к обычному регрессионному уравнению и построить для него МНКоценку вектора коэффициентов. Эта оценка зависит от матрицы ковариаций ошибки ε , а способ оценивания носит название «обобщенный метод

73

наименьших квадратов» (ОМНК). Для ОМНК-оценки устанавливается аналог теоремы Гаусса-Маркова, а именно, доказывается, что в классе всех несмещенных линейных оценок она обладает наименьшей матрицей дисперсий-ковариаций. Обобщенный метод наименьших квадратов позволяет с единых позиций изучать некоторые важные классы регрессионных моделей: так называемые модели с гетероскедастичностью, когда матрица Ω является диагональной, но имеет разные элементы на главной диагонали, и модели, в которых наблюдения имеют смысл временных рядов, а ошибки коррелированы по времени.

Следует подчеркнуть, что практическое использование обобщенного метода наименьших квадратов усложнено тем, что для построения ОМНК-оценки требуется знать матрицу Ω, которая реально почти всегда неизвестна. В связи с этим возникает проблема построения так называемого доступного обобщенного метода наименьших квадратов.

5.1. Обобщенный метод наименьших квадратов

Одно из предположений классической регрессионной модели состоит в том, что случайные ошибки некоррелированы между собой и имеют постоянную дисперсию (см. п. 3.1). В тех случаях, когда наблюдаемые объекты достаточно однородны, не сильно отличаются друг от друга, такое допущение оправдано. Однако во многих ситуациях такое предположение нереалистично. Например, если исследуется зависимость расходов на питание в семье от ее общего дохода, то естественно ожидать, что разброс в данных будет выше для семей с более высоким доходом. Это означает, что дисперсии зависимых величин (а следовательно, и случайных ошибок) не постоянны. Как мы уже указывали (см. п. 2.1), это явление в эконометрике называется гетероскедастичностью (в отличии от гомоскедастичности – равенства дисперсий). Кроме того, при анализе временных рядов, как правило, значение исследуемой величины в текущий момент времени статистически зависит от ее значений в прошлом, что означает наличие корреляции между ошибками. Поэтому естественно

изучать модели регрессии без предположения, что V (ε)=σ 2 In .

Здесь мы будем рассматривать так называемую обобщенную линейную модель множественной регрессии, которая описывается системой

k- число оцениваемых параметров модели, n - число наблюдений); 3а. M (ε)= 0;

3b. M (εεT )=V (ε)= Ω и Ω - симметричная положительно определенная матрица размера n × n ;

74

где Y - (n ×1) вектор зависимых переменных, X - (n × k ) матрица значений независимых переменных, B - (k ×1) вектор неизвестных параметров, ε - (n ×1) вектор случайных ошибок.

Формальная запись такой модели отличается от классической линейной модели множественной регрессии (см. п. 3.1) только условием 3b, т. е. отказом от требования некоррелированности и гомоскедастичности случайных ошибок.

Прежде чем перейти к задаче оценивания вектора параметров B в модели (5.1) выясним смысл гипотезы, в силу которой Ω - положительно определенная матрица.

Как известно, для такой матрицы все главные миноры положительны. Так, для матрицы Ω размера 2 × 2 мы можем записать

тельной дисперсией, а две ошибки не должны полностью коррелировать,

т. е. r122 ≠1.

Задача оценивания может быть решена несколькими эквивалентными способами, из которых мы выбрали простейший.

Известно, что положительно определенная матрица допускает пред-

ставление в виде PPT , где P - матрица невырожденная. Поэтому запишем

модель (5.3) удовлетворяет всем предположениям классической линейной модели множественной регрессии с той лишь разницей, что все

применив к (5.3) обыкновенный МНК, получим

75

подставим значения X * , Y * :

B= (P−1 X )T P−1 X −1 (P−1 X )T P−1Y =

=X T P−1T P−1 X −1 X T P−1T P−1Y =

ˆ

= (X T Ω−1 X )−1 X T Ω−1Y .

Таким образом, оценки по обобщенному методу наименьших квадратов (ОМНК-оценки) определяются соотношением

ные соотношением (5.4), являются оптимальными в смысле теоремы Га- усса-Маркова, т. е. имеют наименьшую матрицу вариаций

но распределены, то этим же свойством будет обладать и ε* , поэтому ОМНК-оценки будут совпадать с оценками, найденными по методу максимального правдоподобия (естественно, при известной матрице Ω).

Заметим, что если мы применим к модели (5.1) обыкновенный МНК,

тельно вектора наблюдений Y и несмещенной, но не будет эффективной, т. е. не будет обладать наименьшей дисперсией.

Для обобщенной регрессионной модели, в отличие от классической,

не может служить удовлетворительной мерой качества подгонки. В общем случае он даже не обязан лежать в интервале [0,1], а добавление или удаление независимой переменной не обязательно приводит к его увеличению или уменьшению.

Еще раз обратим внимание на то, что для применения ОМНК необходимо знать матрицу Ω, которая практически всегда неизвестна. Поэтому вполне естественным кажется такой способ: попытаться оценить матрицу Ω, а затем использовать эту оценку в формуле (5.4) вместо Ω. Этот под-

76

ход составляет суть так называемого доступного обобщенного метода наименьших квадратов. Следует, однако, понимать, что в общем случае матрица Ω содержит n(n +1) / 2 неизвестных параметров (в силу ее сим-

метричности) и, имея только n наблюдений, нельзя получить для нее «хорошую» оценку. Поэтому для получения приемлемых результатов приходится вводить дополнительные условия или ограничения на структуру матрицы Ω.

Далее рассмотрим два важных класса обобщенных регрессионных моделей: 1) – с гетероскедастичными и 2) – автокоррелированными ошибками.

5.2. Обобщенная линейная модель с гетероскедастичностью

Рассмотрим частный случай обобщенной регрессионной модели (5.1), когда Ω = diag(σ12 ,K,σn2 ) есть диагональная матрица с элементами на

главной диагонали σ12 ,K,σn2 , т. е. ошибки в разных наблюдениях некор-

релированы, но их дисперсии различны. Как уже отмечалось, гетероскедастичность довольно часто возникает, если анализируемые объекты, говоря нестрого, неоднородны. Например, если исследуется зависимость прибыли предприятия от каких-либо факторов, допустим, от размера основного фонда, то естественно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых.

Обобщенный метод наименьших квадратов в данном случае выглядит очень просто. Вспомогательная система (5.3) получается делением каждого уравнения системы (5.1) на соответствующее σi (здесь нам

Нетрудно понять содержательный смысл этого преобразования. Используя обычный МНК, мы минимизируем сумму квадратов отклонений

ют разный статистический вклад из-за различных дисперсий, что в конеч-

77

ном итоге и приводит к неэффективности МНК-оценок. «Взвешивая» каж-

1

дое наблюдение с помощью коэффициента σi , мы устраняем такую не-

однородность. Поэтому часто ОМНК для системы с гетероскедастичностью называют методом взвешенных наименьших квадратов. Можно непосредственно проверить, что применение метода взвешенных наименьших квадратов приводит к уменьшению дисперсий оценок по сравнению с обычным МНК.

Если числа σi неизвестны (что, как правило, и бывает на практике), необходимо использовать доступный обобщенный метод наименьших квадратов, который требует оценивания дисперсий σi2 . Так как число

этих параметров равно n , то без дополнительных ограничений на структуру матрицы Ω нет надежды получить приемлемые оценки дисперсий. Такими ограничениями, в частности, могут быть: 1) ошибка пропорциональна одной из независимых переменных; 2) дисперсии ошибок принимают только два значения.

Ограничимся рассмотрением лишь второго случая.

словами, в первых n1 наблюдениях дисперсия ошибки имеет одно значение, в последующих n2 - другое. В этом случае естественным является

следующий вариант доступного ОМНК:

1) обыкновенным методом наименьших квадратов оценить параметры модели (5.1), получить вектор остатков e и разбить его на два подвектора e1 и e2 размерности n1 и n2 соответственно;

2) построить оценки ωˆ12 = e1T e1 n1 и ωˆ 22 = e2T e2 n2 дисперсий ω12 и ω22 ;

3)преобразовать переменные, разделив первые n1 уравнений на ωˆ1,

апоследующие n2 - на ωˆ 2 ;

4)для преобразованной модели вновь использовать метод наименьших квадратов.

Оценки ωˆ12 и ωˆ 22 , полученные таким способом, будут смещенными, но

состоятельными.

Если дисперсия ошибок принимает не два, а несколько значений, то описанная схема может быть обобщена соответствующим образом.

Мы не рассматриваем здесь вопрос о состоятельном оценивании дисперсий в общем случае; более подробное изложение этого можно найти в [3,4]. Отметим лишь, что корректировка оценок параметров модели с учетом гетероскедастичности может привести к существенному уменьшению их дисперсий, т. е. увеличению точности найденных оценок

78

(ОМНК-оценки оказываются более эффективными, более точными, чем МНК-оценки).

В заключение обратим внимание на то, каким образом может быть обнаружена гетероскедастичность. Очень часто появление этой проблемы можно предвидеть заранее, основываясь на характере данных (в этом случае значения переменных в уравнении регрессии значительно различаются в разных наблюдениях). В таких ситуациях можно предпринять соответствующие действия по устранению этого эффекта на этапе спецификации модели, и это позволит сократить или, даже, исключить необходимость формальной проверки. В специальной литературе [3,4,5,8] описываются различные методы проверки гипотезы

H0 :σ12 =σ22 =K=σn2 . Опишем наиболее простой из них [3].

Предполагается, что объем n имеющихся исходных данных достаточно велик, и, в частности, выборка может быть разбита на определенное число ( k ) подвыборок объемов, соответственно, n1,n2 ,K,nk

( n1 + n2 +K+ nk = n ) таким образом, что внутри каждой из подвыборок

значения объясняющих переменных либо совпадают, либо принадлежат одному интервалу группирования. В каждой из подвыборок (либо в каждом из интервалов) определяется среднее значение объясняющей пере-

менной и значение выборочной дисперсии DB(i), строится несмещенная

i =1,K, k . Проверка гипотезы H0 :σ12 =σ22 =Kσn2 сведется к построению

статистического критерия для проверки гипотезы об однородности дисперсий по величинам соответствующих несмещенных их оценок, т. е. исправленных выборочных дисперсий. В качестве такого критерия может быть использован, например, критерий Бартлетта (если ni различны) или

критерий Кохрана (если все ni равны между собой) [1-3]. В случае откло-

нения гипотезы H0 значения Si2 могут быть использованы в качестве

диагональных элементов матрицы Ω, что позволит осуществить обобщенный метод наименьших квадратов, и тем самым улучшить качество оценок параметров модели.

5.3. Обобщенная линейная модель с автокоррелированными остатками

До сих пор предполагалось, что случайные ошибки в разных наблюдениях некоррелированы, т. е. cov(εiε j )= 0 , i ≠ j . Так как мы предпола-

гаем, что M (εi )= 0 , i =1,K, n , то cov(εiε j )= M (εiε j )= 0 , i ≠ j . Когда дан-

ное условие не выполняется, говорят, что случайные ошибки или остатки подвержены автокорреляции, которую часто называют сериальной кор-

79

реляцией (эти два термина взаимозаменяемы). Последствия автокорреляции в некоторой степени сходны с последствиями гетероскедастичности. Оценки параметров регрессионной модели остаются несмещенными, но становятся неэффективными, и их стандартные ошибки оцениваются неправильно, занижаются.

Автокорреляция обычно встречается только в регрессионном анализе при использовании данных временных рядов. Случайная составляющая

εв уравнении регрессии подвергается воздействию тех переменных, которые влияют на зависимую переменную, но не включены в модель. Если ошибки некоррелированы, то и значения любой переменной, «скрытой» в

εдолжны быть некоррелированными.

Постоянное воздействие переменных или факторов, не включенных в модель, является наиболее частой причиной положительной автокорреляции, которая наиболее типична для экономического анализа. Предположим, что мы оцениваем уравнение спроса на мороженое по ежемесячным данным, и такой важный фактор, как температура воздуха, не включен в модель. Естественно, у нас будет несколько последовательных наблюдений, когда теплая погода способствует увеличению спроса на мороженое и, таким образом, ε > 0 ; после этого может быть несколько последовательных наблюдений, когда ε < 0 , затем опять идет еще один ряд теплых месяцев и т. д.

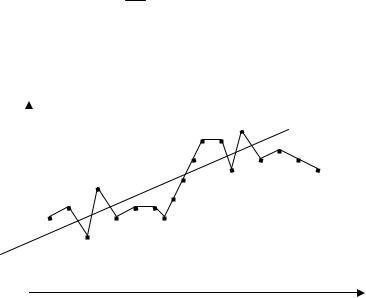
Если доход постоянно возрастает со временем, то схема наблюдений может быть такой, как показано на рис. 5.1. Здесь через y обозначен

лето

зима

зима

x

Рис. 5.1. Положительная автокорреляция Изменения экономической конъюнктуры часто приводят к похожим

результатам, особенно наглядным в макроэкономическом анализе. Отметим, что чем меньше интервал между наблюдениями, тем суще-

ственнее проблема автокорреляции. Очевидно, чем больше этот интервал, тем менее правдоподобно, что при переходе от одного наблюдения к другому характер влияния неучтенных факторов будет сохраняться.

Если в нашем примере с мороженым наблюдения проводятся не ежемесячно, а ежегодно, то автокорреляции, вероятно, вообще не будет.

80