Дифференциал функции

Литература.[1], [2], [6], [7], [17].

Понятие дифференциала функции, его геометрический смысл

Пусть функция дифференцируема на отрезке. Производная этой функции в некоторой точкеотрезкаопределяется равенством:. Тогда, по теореме о связи функции, её предела и бесконечно малой функции, можно записать, гдепри, или.

Приращение функции состоит из двух слагаемых, из которых первое есть так называемая главная часть приращения, линейная относительно.

Дифференциалом функции в точкеназывается главная часть её приращения, которая равна произведению производной функции на приращение аргумента, и обозначаетсяили:.

Дифференциал называют также дифференциалом первого порядка.

Дифференциал независимой переменной равен приращению этой переменной: и тогда, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Пример 1.Найти дифференциал функции.

Решение:По формуленаходим

.

Основные теоремы о дифференциалах. Таблица дифференциалов.

Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяется формулами:

Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточной переменной на дифференциал этой промежуточной переменной

.

Таблица дифференциалов

Применение дифференциала в приближенных вычислениях

.

Пример 2. Вычислить приближенно.

Решение. Рассмотрим функциюf(x)=arctg x.

По формуле имеем:

,

т.е.

.

Так как , то прииполучаем:

.

Вопросы для самопроверки

1.Что называется дифференциалом функции, каков его геометрический смысл?

2. Сформулируйте основные свойства дифференциала функции.

3. Чем отличается дифференциал функции от ее приращения?

4. Укажите формулу для приближенного вычисления значений функции с помощью дифференциала.

5. Что называется дифференциалом второго порядка от данной функции?

Приложения производной

Литература.[1], [2], [6], [7], [17].

Применение производной к вычислению пределов.

Кроме элементарных способов, весьма эффективным средством для нахождения предела функции в тех случаях, когда аргумент неограниченно возрастает или стремится к значению, которое не входит в область определения функции, является правило Лопиталя.

Теорема.Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если он существует или равен бесконечности.

Итак, если имеются неопределенности вида или, то

.

Обращаем внимание, что в правой части формулы берется отношение производных, а не производная отношения.

Пример.Найти: а)б)в)

Решение.а) Имеем неопределенность вида. Применяя правило Лопиталя, получим:

б)

Неопределенность вида по-прежнему сохраняется. Применим правило Лопиталя еще раз:

в) Имеем неопределенность вида . Переписываем данное выражение в виде

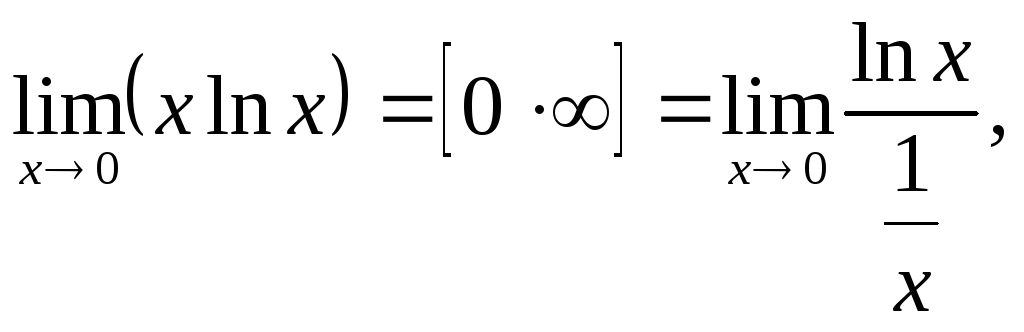
получим неопределенность вида . Применяя правило Лопиталя, получим

.

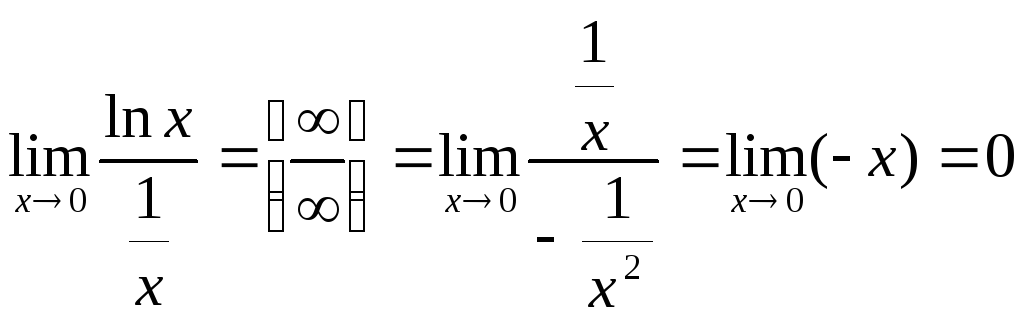Применение производной к исследованию функций Возрастание и убывание функций

При изучении поведения функции в зависимости от изменения независимой переменной обычно предполагается, что во всей области определения функции независимая переменная изменяется монотонно возрастая, т.е. что каждое следующее ее значение больше предыдущего.

Если при этом последовательные значения функции также возрастают, то и функция называется возрастающей, а если они убывают, то и функция называется убывающей.

Некоторые функции во всей своей области определения изменяются монотонно – только возрастают или только убывают (например ).

Многие функции изменяются не монотонно. В одних интервалах изменения независимой переменной они возрастают, а в других интервалах убывают (например, sinx,cosx).

Возрастание и убывание функции характеризуется значением ее производной: если в некотором интервале>0, то функция возрастает, а если<0, то функция убывает в этом интервале.