Бесконечно малые функции (б.М.Ф.)

Функция у = f(х) называется бесконечно малой при х → х₀, если

По определению предела функции это равенство означает: для любого числа ε > 0 найдется число δ > 0 такое, что для всех х, удовлетворяющих неравенству 0 < |х – х₀| < δ, выполняемся неравенство  f(х) < ε.

Аналогично определяется б.м.ф. при х → х₀ + 0, x → х₀ – 0, х → + , х → –  : во всех этих случаях f(х) → 0.

Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами α, β и т. д.

Примерами б.м.ф. служат функции у = х² при х→0; у = х – 2 при х→2; у = sin x при х → . Другой пример:х_n = – бесконечно малая последовательность.

Теорема 1.Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

Теорема 2. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.

Следствие 1.Так как всякая б.м.ф. ограничена, то из теоремы 2 вытекает: произведение двух б.м.ф. есть функция бесконечно малая.

Следствие 2. Произведение б.м.ф. на число есть функция бесконечно малая.

Теорема 3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.

Теорема 4 (связь между бесконечно малыми и бесконечно большими функциями). Если функция (х) – бесконечно малая ( ≠ 0), то функция – есть бесконечно большая функция и наоборот: если функцияf(x) – бесконечно большая, то – бесконечно малая.

Теорема 5 (связь между функцией, ее пределом и бесконечно малой функцией). Если функция f(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции (х), т.е. если , тоf(х) = А + (х).

Теорема 6 (обратная). Если функцию f(х) можно представить в виде суммы числа А и бесконечно малой функции (х), то число А является пределом функции f(х), т.е. если , то .

Основные теоремы о пределах

В приводимых теоремах будем считать, что пределы ,существуют.

Теорема 1.Предел суммы (разности) двух функций равен сумме (разности) их пределов

.

Теорема справедлива для алгебраический суммы любого конечного числа функций.

Следствие. Функция может иметь только один предел при х → х₀.

Теорема 2.Предел произведения двух функций равен произведению их пределов:

.

Теорема справедлива для произведения любого конечного числа функций.

Следствие 1.Постоянный множитель можно выносить за знак предела:

.

Следствие 2. Предел степени с натуральным показателем равен той же степени предела: . В частности,.

Теорема 3.Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю

.

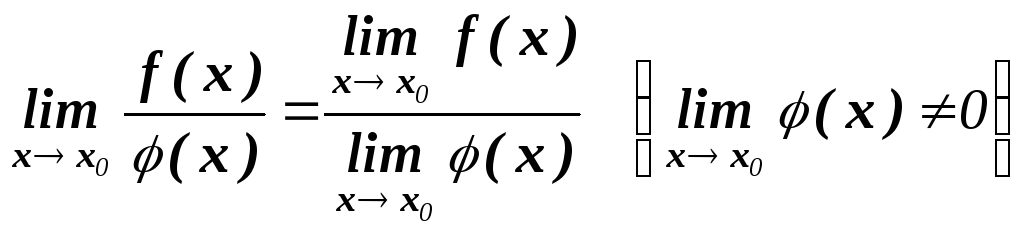Пример 1.Вычислить .

Решение:

.

Пример 2. Вычислить .

Решение: Здесь применить теорему о пределе дроби нельзя, т.к. предел знаменателя, при х → 2, равен 0. кроме того, предел числителя равен 0. В таких случаях говорят, что имеет неопределенность вида . Для ее раскрытия разложим числитель и знаменатель дроби на множители, затем сократим дробь на х – 2 ≠ 0 (х → 2, но х ≠ 2):

.

Пример 3. Вычислить .

Решение: Здесь мы имеет дело с неопределенностью вида . Для нахождения предела данной дроби разделим числитель и знаменатель на х².

.

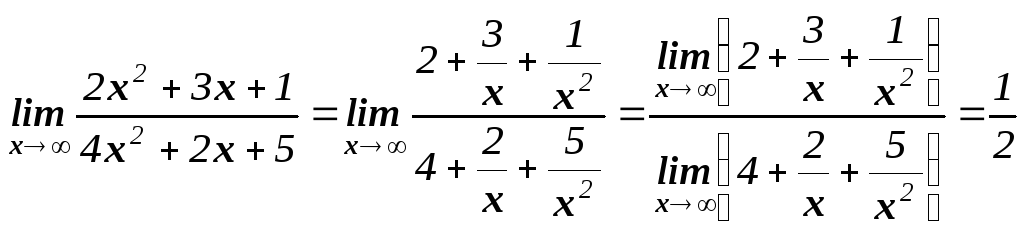Функция есть сумма числа2 и б.м.ф., а функция есть сумма числа4 и б.м.ф., поэтому

,.