откуда y2 = 2px. Полученное уравнение называется каноническим уравнени-

ем параболы.

Элементами параболы являются: точка О - вершина параболы; OX - ось параболы; точка F(р/2,0) - фокус параболы; x = − 2p - уравнение директри-

сы параболы; e =1- эксцентриситет параболы; p - фокальный параметр

(расстояние от фокуса до директрисы или половины хорды, проходящей через фокус перпендикулярно оси OX).

6.4. Преобразования координат

6.4.1. Параллельный перенос

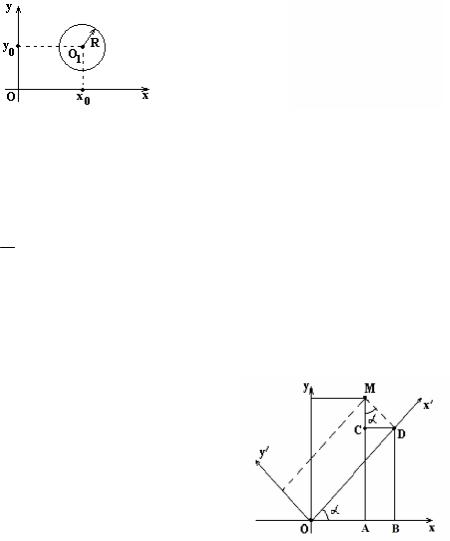
Перенесём начало координат из точки О в точку О1 параллельным переносом осей. Пусть в системе координат xOy точка М имеет координаты x и y. Система координат x′O1y′ получена из системы координат xOy параллельным переносом осей, при котором начало координат О1 имеет координаты x0 и y0 в системе координат xOy. Точка М в системе коор-

динат x′O1y′ имеет координаты x′ и y′. Связь между координатами точки M(x,y) и точки M(x′,y′) в старой и новой системах координат задается формулами:

Уравнения кривых второго порядка, когда их центры симметрии находятся в точке с координатами O1(x0,y0), получаются с помощью преобразования координат при параллельном переносе осей (2).

(x − x0 )2 + ( y − y0 )2 = R2 - уравнение окружности с

центром в точке O1(x0,y0) и радиусом R. Аналогично получаются уравнения других

кривых второго порядка:

шиной в точке O1(x0,y0).

При этом, например, уравнения директрис эллипса и гиперболы: x − x0 = ± ae ,

а параболы: x − x0 = − 2p . Аналогично преобразуются и уравнения асимптот гиперболы: y − y0 = ± ba (x − x0 ) .

6.4.2. Поворот координатных осей

Выведем формулу преобразования координат при повороте координатных осей.

Повернём оси координат на угол α относительно исходной системы координат. Координаты точки М в системе координат x′Oy′ равны x′ и y′. Найдём её координаты в системе координат xOy. В треугольнике CMD CMD = α , OD = x′, MD = y′.

Следовательно,

Эти формулы выражают старые координаты (x,y) произвольной точки М через новые координаты (x′,y′) этой же точки при повороте осей на угол α. Формулы, выражающие новые координаты (x′,y′) точки М через её старые координаты (x,y), получим из следующих соображений: если новая система

Кривые второго порядка, имеющие единственный центр, называются центральными. После переноса начала координат в центр (x0,y0) уравнение кривой примет вид

где F1 = Dx0 + Ey0 + F .

Чтобы получить каноническое уравнение кривой

A1 (x′′) 2 + C1 ( y′′) 2 + F2 = 0 ,

подвергнем уравнение (7) преобразованию поворота осей координат на угол α .

После преобразования получим:

x′ = x′′cosα − y′′sinα, y′ = x′′sinα + y′′cosα,

где x′′, y′′ - новые координаты.

Выпишем из преобразованного уравнения слагаемые второго порядка:

A(x′′cosα − y′′sinα)2 + 2B(x′′cosα − y′′sinα)(x′′sinα + y′′cosα) +C(x′′sinα + y′′cosα)2 .

Из этих слагаемых нас интересует слагаемое, содержащее произведение x′′ y′′ , коэффициент перед которым равен

6.5*. Линии в полярной системе координат

6.5.1*. Полярные координаты на плоскости

Полярные координаты определяются заданием на плоскости полюса О и полярной оси ρ.

Координаты точки М в полярных координатах задаются длиной радиус-вектора OM = ρ этой точки и углом его наклона к полярной оси. При этом 0 ≤ ρ ≤ ∞, 0 ≤ ϕ ≤ ∞.