8.1.2. Параметрическое задание линий

8.1.4. Полярные координаты на плоскости

8.1.5. Связь полярных координат с декартовыми

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции по математике.pdf

Скачиваний:

918

Добавлен:

14.02.2015

Размер:

9.7 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

258	Лекции 7 - 8

Пример:

Вычислить площадь эллипса x2 + y2 =1. a2 b2

y = ±b 1−	x2	,
y = ±b 1−	a2	,
	a2
a			x2					π
Sэл = 4∫b 1−					dx = x = a sin t,α		= 0, β =		=
Sэл = 4∫b 1−			a	2	dx = x = a sin t,α		= 0, β =	2	=
0			a					2
π
= 4ab∫2 cos2 tdt = [2abt + absin 2t]						π	= πab , Sэл =πab.
						π
						02
0

Параметрические уравнения линий задаются в виде зависимости координат x и y от некоторого параметра t: x = x(t), y = y(t) . При изменении пара-

метра t текущая точка M(x, y) описывает некоторую кривую на плоскости. Исключением параметра уравнение линии приводится к уравнению в декартовых координатах и, наоборот, линия, заданная в декартовых координатах, может быть приведена к виду кривой, заданной параметрическими уравнениями.

8.1.3.Вычисление площадей фигур, граница которых задана кривыми в параметрической форме

Пусть кривая задана параметрическими уравнениями:

x = x (t),		(	)	, b = x	(	β	)	.
		(	)		(		)
		α ≤ t ≤ β , a = x α
y = y (t),

b	b				β
S = ∫ f (x)dx = ∫ ydx ={x = x (t), dx=x′			(t )dt}= ∫ y (t )x ' (t)dt ;
a	a				α

S = ∫y (t )x '(t )dt .

Пример:

Вычислить площадь эллипса.

Уравнения эллипса в параметрической форме имеют вид:

x = a cos t , 0 ≤ t ≤ 2π .

y = b sin t

Определенный интеграл

259

Решение:

S = 4S = 4∫2

ab sin2 tdt =

sin 2t

= 2ab∫(1−cos 2t )dt = 2ab

= πab.

t −

Пример:

Найти площадь фигуры, ограниченную первой

аркой циклоиды х = а (t − sin t); у = а (1 − cos t) и

отрезком оси абсцисс

Решение:

Точкам О и А соответствуют значения параметра

πa

2πa

tО = 0 и tА = 2π, поэтому искомая площадь равна

2π a (1−cost ) a

(1−cost ) dt = 2π a2 (1−cos t )2 dt =

∫

2π

1+cos 2t

t −2sin t +

2π

∫0

1−2cos t +

dt = а

sin 2t

= 3πa

Полярные координаты определяются заданием на плоскости полюса О и полярной оси ρ .

Координаты точки М в полярных координатах за-

JJJG

даются длиной радиус-вектора OM = ρ этой точки

и углом его наклона к полярной оси. При этом

0 ≤ ρ < ∞, 0 ≤ϕ ≤ ∞ .

Определенный интеграл

Совместим начало декартовой системы с полюсом полярной системы координат, а ось Оx с полярной осьюρ . Найдём связь координат точки

M(x,y) и M( ρ ,ϕ). Она выражается следующей системой уравнений:

x = ρ cosϕ,	ρ = x2 + y2 ,
		y
y = ρsinϕ,	tgϕ =		.

		x

260	Лекции 7 - 8
8.1.6. Примеры уравнений линий в полярной системе координат
Уравнение вида ρ = ρ(ϕ), задающее ρ как функцию ϕ , определяет на
плоскости некоторую кривую.

Пример:
	Архимедова спираль: ρ =аϕ, 0 <ϕ < ∞, ρ ≥ 0 .
	Архимедова спираль: ρ =аϕ, 0 <ϕ < ∞, ρ ≥ 0 .
	Решение:
		ϕ	0	π	π	2π	5π
		ϕ	0	2	π	2π	2
				2			2
		ρ	0	π	a π	2aπ	5aπ
			0	a 2	a π	2aπ	2

!Кривая представляет собой путь, описываемый точкой, движущейся с постоянной скоростью по лучу, вращающемуся около полюса О, с по-

стоянной скоростью ω : a = ωv .

Пример:

Окружность со смещенным центром:														ρ = a cosϕ .
Решение:
ϕ		0					π				π	π	3π					7π		2π
ϕ		0						4			2	π		2		4				2π
								4			2			2		4
cosϕ		1						2			0	-1		0				2		1
cosϕ		1						2			0	-1		0		2				1
								2								2
ρ		a						2			0	0		0			2			a
ρ		a					2 a											2 a		a
							2 a											2 a
Координата ρ принимает только положительные значения.
Поскольку cosϕ =									ρ	значит, угол ОМА - прямой.
Поскольку cosϕ =									a	значит, угол ОМА - прямой.
									a	ρ = a cosϕ
Вывод:		уравнение								ρ = a cosϕ		задает			окружность					с центром в точке
(a/2,0) и радиусом a/2.
Преобразуем:					ρ = a cosϕ , ρ ρ = a ρ cosϕ ;
Преобразуем:					ρ = a cosϕ , ρ ρ = a ρ cosϕ ;
ρ2	= aρ cosϕ ;

x2 +y2
x2 + y2 = ax ; x2 + y2 −ax + a2 − a2 = 0 .
	a 2	+ y	2			a		2
	a 2		2			a		2		-	каноническое уравне-
x −				=						-	каноническое уравне-
	2					2
ние окружности с центром в точке ( a														,0) радиусом					a .
													2						2

Определенный интеграл

261

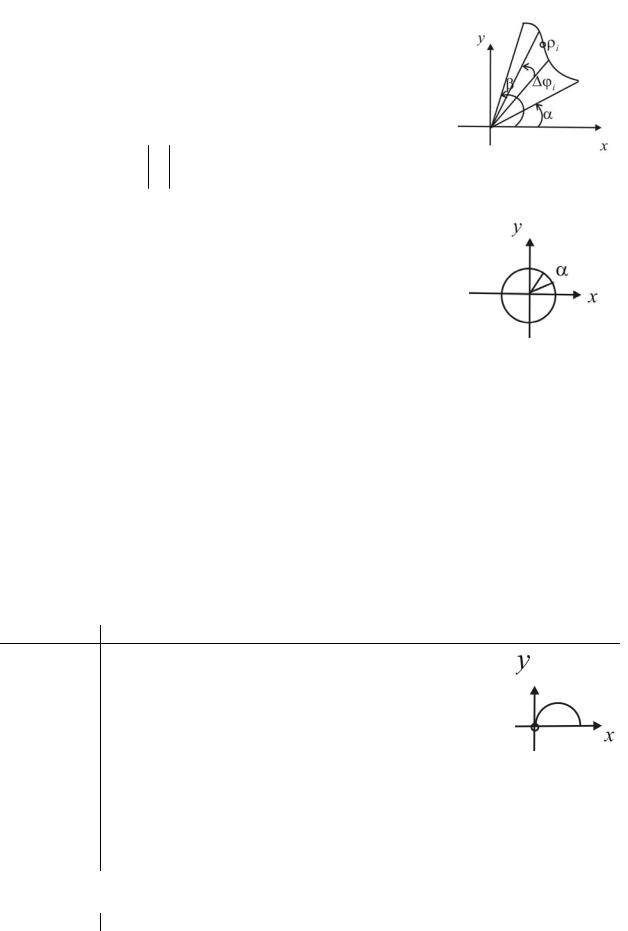
8.1.7. Площадь криволинейного сектора в полярной системе координат

Пусть ρ = ρ(ϕ) - непрерывная функция. Опре-

делим площадь криволинейного сектора, ограниченного кривой ρ = ρ(ϕ) и лучами ϕ =α , ϕ = β .

Разобьем указанный сектор лучами на сектора вели-

→

чины +ϕi . Пусть ρi = ρi - величина радиус-вектора

для произвольного ϕi				[ϕi ,ϕi+1 ].
Лемма: Площадь кругового сектора равна Sα =							r2	α .
Лемма: Площадь кругового сектора равна Sα =							2	α .
Доказательство следует из пропорции:							2
Доказательство следует из пропорции:
	Sкруга =πr2 → 2π;
	Sα → α;
	Sα =	απr2	=	αr2	.
	Sα =	2π	=	2	.
		2π		2		сектора Si	равна
Тогда	площадь		кругового			сектора Si	равна
Si = 1					n
Si = 1	ρi2 +ϕi ; сумма		Q = ∑1 ρi2			+ϕi - площадь ступен-
2				i=1 2

чатого сектора, спрямляющего криволинейный сектор. При n →∞ Q → S , Q - интегральная сумма, то-

1 β

гда S = 2 α∫ρ2dϕ - площадь криволинейного сектора.

Пример:

Вычислить площадь круга ρ = 2a cosϕ .

В силу симметрии достаточно вычислить 1/2 искомой площади.

S =	2 π∫/ 2				ρ2dϕ = π∫/ 2 (2a)2 cos2 ϕdϕ = π∫/ 2												4a2 1+cos 2ϕ dϕ =
	2		0					0								0					2
		2	π / 2 dϕ				π	/ 2	cos 2ϕ				2	ϕ			π / 2		1			π	/ 2
= 4a		2	π / 2 dϕ			+		∫	cos 2ϕ			= 4a	2	ϕ			π / 2	+	1		sin 2ϕ	π	/ 2	=
= 4a				∫	2	+		∫	2		dϕ	= 4a				2	0	+	4		sin 2ϕ	0		=
				0	2			0	2							2			4
= 4a		2		π	−0	+	1	sin π −		1					2 π				2	.
= 4a				4	−0	+	4	sin π −		4	sin 0 = 4a					4	=πa			.
				4			4			4						4

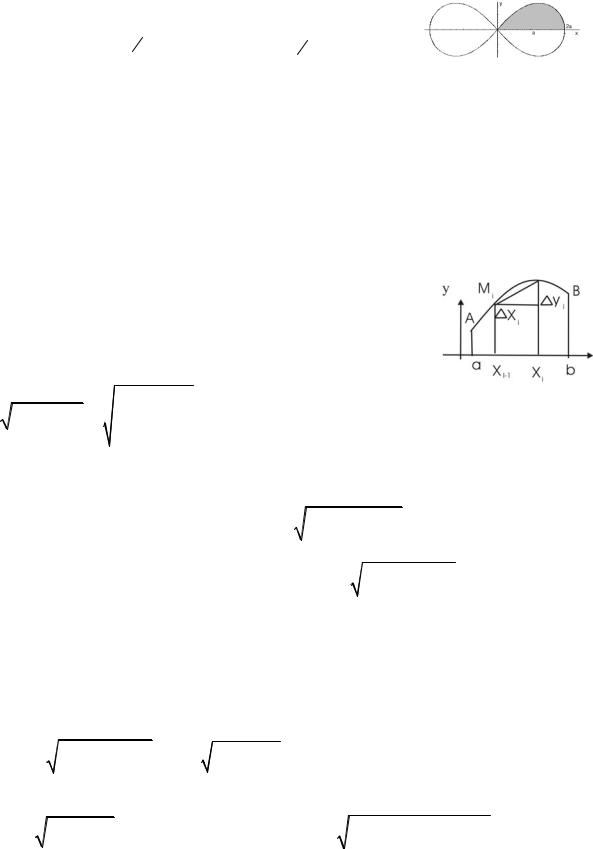
Пример:

262

Лекции 7 - 8

Найти площадь, заключённую внутри лемнискаты Бернулли

ρ2 = а2 сos2ϕ .

Решение:

В силу симметрии достаточно

вычислить одну четверть искомой площади:

π 4

a2 sin 2ϕ

π 4

a 2

S =

∫

cos 2ϕdϕ =

откуда S = а2.

8.2. Вычисление длины дуги кривой

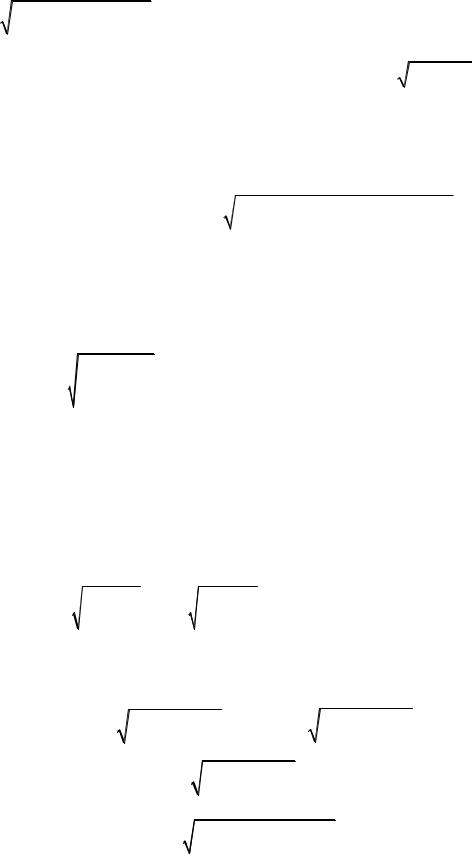
8.2.1. Вычисление длины плоской кривой в прямоугольных координатах

L : y = f (x).

Разобьем

[a,b]

на

части

a = x0 < x1 < x2 <... < xn = b .

На кривой обозначим точки A, M1,..., Mn−1, B . Соеди-

ним их хордами. Получим ломаную, состоящую из n хорд.

l =

++y2

= 1+

+yi

длина

i -

хорды,

+xi

- длина ломаной. По теореме Лагранжа ( f (b)− f (a) = f '(c)(b − a))

ln = ∑li

i=1

+yi = f '(ξ

[x −

], l

1 + f '(ξ

) 2

имеем:

, x

∑

+x .

+xi

i=1

2 dx .

Пусть max+xi

→ 0 , ln

∫

→ l , следовательно,

l =

1 + f '(x)

8.2.2. Вычисление длины плоской кривой в параметрической форме

x = x(t )

L : y = y(t ) α ≤ t ≤ β (a = x(α);b = x(β ));

(

)

[

]

{

(

)

}

l =

∫

x = x

, dx = x ' dt

1+ f '

2 dx =

' 2 dx =

= ∫

[

' 2 x '

(

)

dt =

' = dy

yt '

x '

(

+ y '

(

2 dt ,

x '

∫

]

)

Если кривая задана в полярных координатах, то l = ∫ ρ2 + ρ′2 dϕ .

8.2.3.Вычисление длины дуги пространственной кривой

впараметрической форме

x = x(t )

L : y = y(t ) α ≤ t ≤

z = z (t )

	β	x '(t ) 2	+ y '(t ) 2	+ z '(t ) 2 dt
β , l =	∫	x '(t ) 2	+ y '(t ) 2	+ z '(t ) 2 dt
	∫

Пример:

L : y = ln 1− x2

)

; a = 0,b = 1 ;l −?

(

4x2

x2 +1

1+ x

l =

dx =

dx = −x +ln

02 = ln 3 −

∫

(

)

∫1− x

x −1

2 .

1− x

Пример:

= a cos t

= a sin t

- винтовая линия. lвитка =?

= 2π t

l = 2∫π

a2 +

2 dt = 2π a2 +

c 2

4π

8.2.4. Дифференциал длины дуги кривой

l (x)= x

1 + f '(x) 2 dx ;

l '(x)= 1+ f '(x) 2

;

∫

dl = 1+ f '(x) 2 dx .

В параметрической форме:

dl =

x'(t )

2 + y '(t ) 2 dt .

264 Лекции 7 - 8

8.2.5. Длина кривой, заданной в полярных координатах
Пусть уравнение кривой в полярных координатах ρ = ρ(ϕ). Можно рас-
сматривать уравнения x = ρ cosϕ				как параметрические уравнения линии L,
		y = ρsinϕ
	β				β	x ' (ϕ) 2	+ y ' (ϕ) 2 dϕ .
имеющей длину l =	∫	x '2	+ y '2 dt , l =		∫	x ' (ϕ) 2	+ y ' (ϕ) 2 dϕ .
	∫	t	t		∫
	α				α
x 'ϕ = ρ 'cosϕ − ρsinϕ ,

y 'ϕ = ρ 'sinϕ + ρ cosϕ .

x 'ϕ 2 + y 'ϕ 2 = (ρ 'cosϕ − ρ sinϕ )2 + (ρ 'sinϕ + ρ cosϕ)2 = ρ '2 + ρ2 ,

β			β
l = ∫	(x 'ϕ )2 + (y 'ϕ )2 dϕ = ∫ ρ '2 + ρ2 dϕ .
α			α
Пример:
Пример:
		Вычислить длину окружностиρ = 2a cosϕ .
		π / 2			π / 2
		L = 2 ∫	(−2a sinϕ)2 + 4a2 cos2 ϕdϕ = 4a ∫			cos2 ϕ +sin2 ϕdϕ =
		0			0
		= 4aπ∫/ 2 dϕ = 4a ϕ		π0 / 2 = 4a π	= 2πa.
		= 4aπ∫/ 2 dϕ = 4a ϕ		π0 / 2 = 4a π	= 2πa.
		0		2

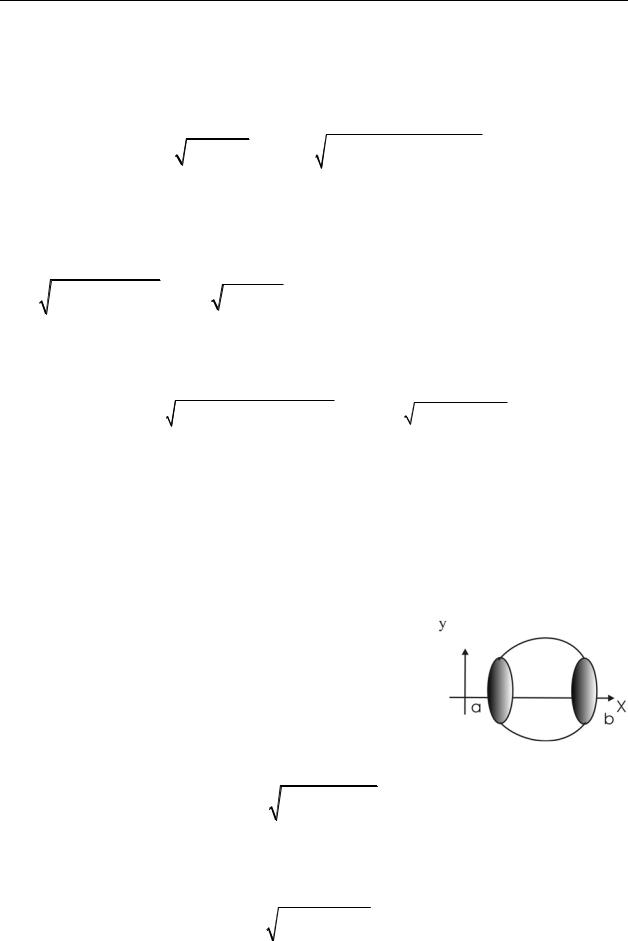
8.2.6. Площадь поверхности вращения

Вычислим Qx – площадь поверхности, образованной вращением кривой y = f (x) вокруг оси Ох).

Разделим отрезок [a, b] точками деления xi . Точке xi соответствует точка на кривой Mi .

Соединим точки на кривой хордами (li ).

При вращении каждая хорда описывает усеченный конус. Площадь его поверхности:

Q =

2π

yi−1 + yi

;

= 2π

yi−1 + yi

1+ f

'(ξi ) 2

+xi ;

Qn = ∑Qi ;

i=1

max+xi → 0 ; Qn → Qx .

(

)

(

)

→ 2π

∫

1 + f '

x 2 dx

Определенный интеграл

265

(

)

(

)

2 dx

= 2π

∫

- площадь поверхности, образованной враще-

1 + f '

нием кривой, заданной функцией у = f (x), а ≤ х ≤ b .

Если дуга задана параметрическими уравнениями х = х (t), у = у (t), t1 ≤ t ≤ t2 ,

то Qх = 2π	t2		′		2		′	(t )		2	dt .
			′		2		′			2
	∫	y(t ) x (t )				+ y
	∫
	t1
Если дуга	β	задана в		полярных					координатах ρ = ρ (ϕ), α ≤ ϕ ≤ β,
то Qх = 2π	β	ρ(ϕ)sinϕ		ρ2 + ρ′(ϕ) 2 dϕ .
	∫

Пример:

Найти площадь поверхности, образованной вращением астроиды х2/3 + у2/3 = а2/3 вокруг оси Ох.

Решение:

2/3

3/2

2/3

2/3 ½

−1/3

(a2 3 − x2 3 )1 2

у = (а

− х ) , у′ =

(а

− х )

( −

) =

−

x1 3

1+ a 2 3 − x 2 3

a1 3

x 2 3

1 3

Следовательно Qх = 2 2π ∫a (a2 3 − x2 3 )3 2

a1 3

dx =

1 3

1 3 a

2 3

)

3 2

−1 3

1/3 3 (a 2 3 − x 2 3 )5 2

= 4πa

∫

− x

= − 4πа

πа

5 2

Пример:

Найти площадь поверхности, образованной вращением одной арки цик-

лоиды х = а (t − sin t), у = а (1− cos t) вокруг оси Ох.

Решение:

Дифференцируем х′ = а (1 − cos t), у′= а (sin t),

′

) =

(1−cos t )

) +(y

+ a

sin

t = а

2(1 − cos t) = 2а sin 2 .

2π

2 t

Qх = 2π

∫ a (1−cos t )2a sin

dt = 8πа

∫

−cos

sin

cos

3 t

2π

−

= − 16πа

cos

πа

266 Лекции 7 - 8

Пример:
	Найти площадь поверхности, образованной вращением
	кардиоиды ρ = 2а (1+ cosϕ) вокруг полярной оси.
	Решение:
	Имеем ρ′ = −2а sin ϕ,
	((ρ′)2 + ρ2 )=			4a2 (1+ cosϕ)2 + 4a2 sin2 ϕ = 4а сos		ϕ .
						2
	Qх =2ππ∫2a (1+cosϕ)sinϕ 4a cos ϕ dϕ =
	0				2
	= 64 πа2	π∫cos4 ϕ sin ϕ dϕ			= 128πa2 .
		0	2	2	5

8.3. Вычисление объемов тел

8.3.1. Вычисление объемов по заданным площадям поперечных сечений

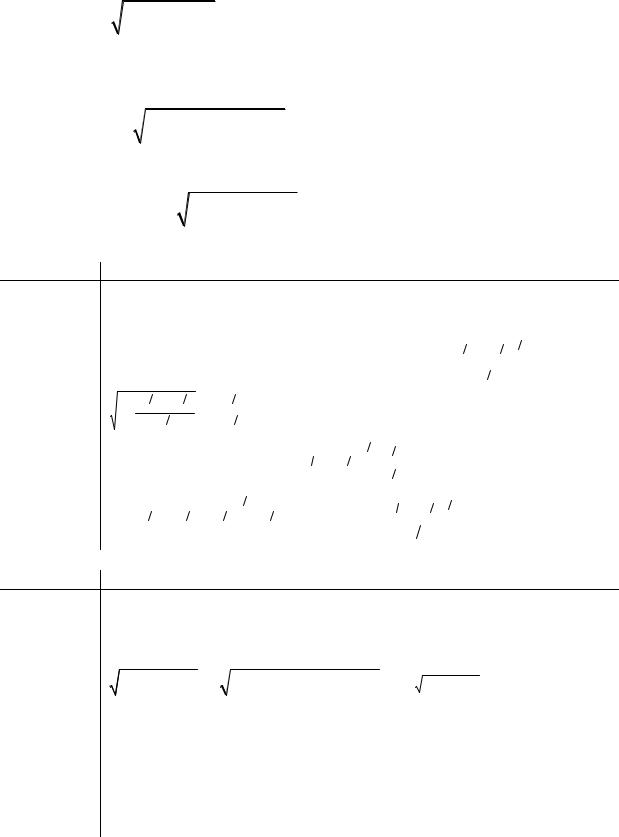
Пусть имеем некоторое тело Т. Предположим, что известна площадь любого сечения этого тела плоскостью, перпендикулярной оси Ох.

Эта площадь зависит от положения секущей плоскости, то есть является функцией х: S =S(x).

Пусть S (x) непрерывна на [a, b]. Разобьем [a, b]

точками деления a = x0 < x1 < x2 <... < xn = b ; через точки xi проведем сечения, перпендикулярные

оси Ох. Площади соответствующих поперечных сечений - S (xi ).

n
Составим сумму: Vn = ∑S (ξi )+xi , ξi [xi−1, xi ], S (ξi )+xi - объем цилинд-
i=1
ра с площадью основания S	(ξi ) и высотой +xi .
Пусть max+xi → 0 , тогда	Vn →V (объем тела). С другой стороны,

Vn → ∫b S (x)dx (Vn - интегральная сумма для непрерывной функции S (x)).

Таким образом, V = ∫b S (x)dx .

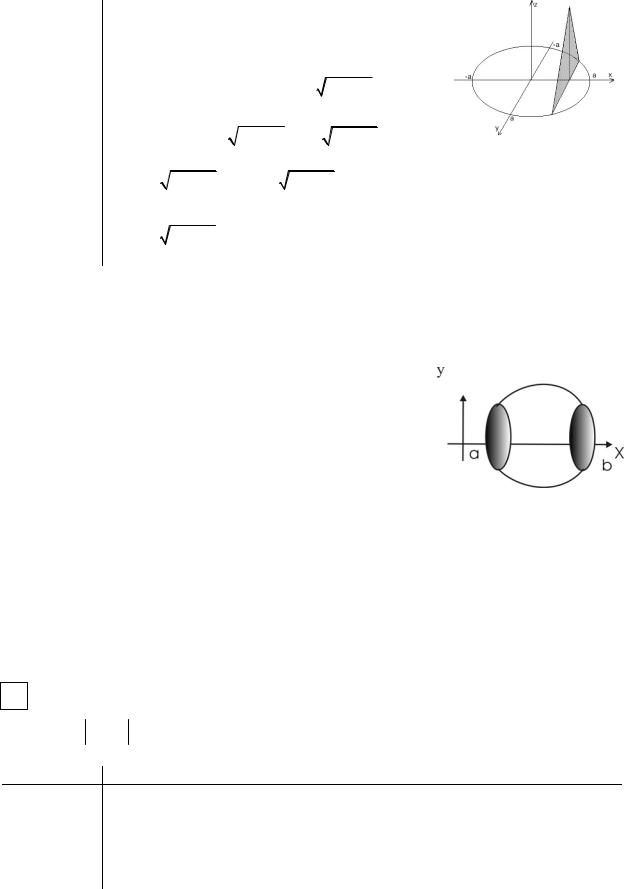
Пример:

Найти объём тела, основание которого - круг радиусом а, а сечение плоскостью, перпендикулярной фиксированному диаметру круга, есть равнобедренный треугольник высотой h.

Решение:

Определенный интеграл

267

Выберем систему координат, начало которой совпадает с центром круга.

Тогда сечение тела плоскостью, перпендикулярной оси Ох, есть равнобедренный тре-

угольник с основанием 2у = 2

a2 − x2

и вы-

сотой h;

имеем S(х) =

a2 − x2 h = h

a2 − x2

V = h ∫a

a2 − x2 dx = 2h∫a

a2 − x2 dx =

−a

πa2h

= 2h

− x

arcsin

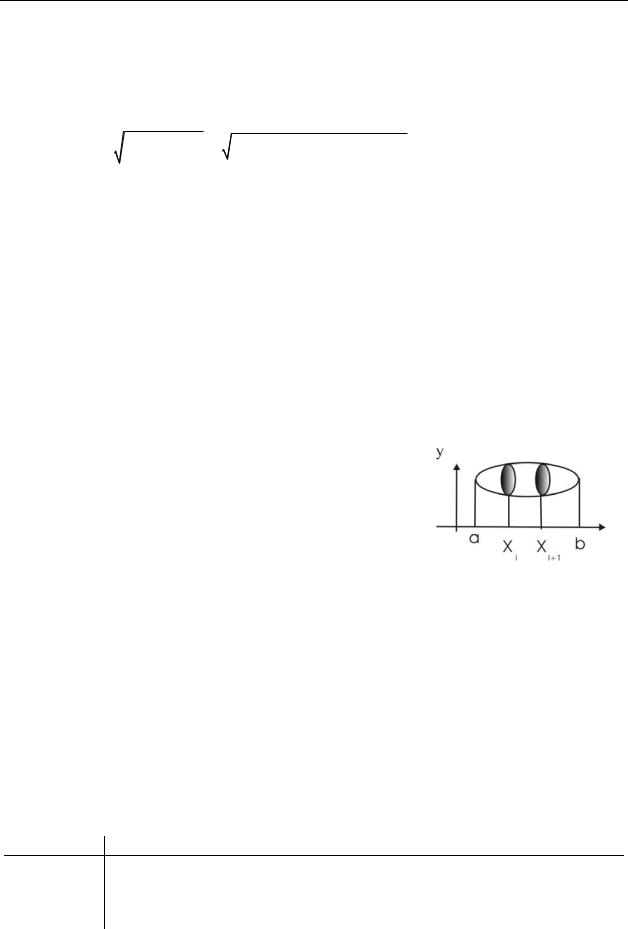
8.3.2. Вычисление объемов тел вращения

Если криволинейная трапеция, ограниченная кривой у = f (x), а ≤ х ≤ b, вращается вокруг оси

Ох, то объём тела вращения вычисляется по формуле:

Vx = ∫b S (x)dx ={S (x)= π f 2 (x)}=π ∫b		f 2 (x)dx .
a	a
Если криволинейная трапеция, ограниченная
кривой x = f (y), c ≤ y ≤ d, вращается вокруг оси Оу, то Vy =π ∫d			f 2 (y)dy .

Если криволинейный сектор, ограниченный кривой ρ = ρ(ϕ) и лучами

2 β

ϕ =α и ϕ = β , вращается вокруг полярной оси, то V = 3 πα∫ρ3 sinϕdϕ .

!Величина Vу может быть также вычислена интегрированием по х: Vу =

2π ∫b x f (x) dx ,

Пример:

Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривой у2 = (х − 1)3 и прямой х = 2 Решение:

2	2	1
Vх = π ∫y2dx = π ∫(x −1)3 dx =		1	π .
1	1	4

268

Лекции 7 - 8

Пример:

Найти объем тела эллипсоида

=1.

Решение:

V = 2∫S

(x)dx =

дляфиксированного x имеемэллипс

−

или

=1,

b12

c12

гдеb1 = b 1−

, c1 = c

1−

(x)

=πb c =πbc 1

−

= 2πbc

−

dx = 2πbc

x −

πabc ,

∫0

V = 4 πabc ,

= 4 πR3

эл

сф

Пример:

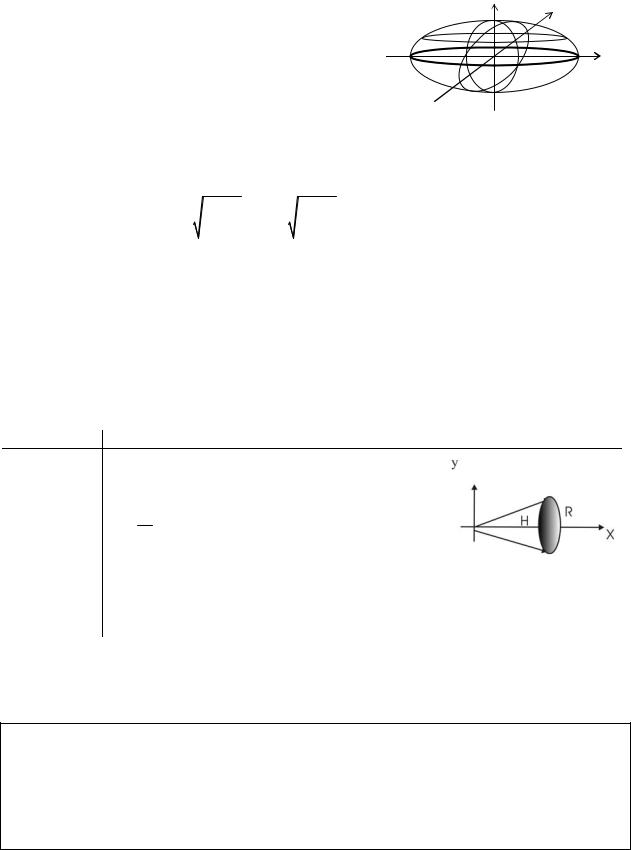
Найти объем конуса с высотой Н и радиусом основания R.

Решение: y = HR x

π R2

Vx =π ∫0

dx =

H 2

π R

H 2

V = 1

π R2 H .

кон

В результате изучения материала, изложенного в этих лекциях, студенты должны знать:

формулу Ньютона-Лейбница;

особенности применения основных методов интегрирования при вычислении определенных интегралов;

геометрические приложения определенного интеграла.

Лекция 9 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

При введении понятия определенного интеграла предполагалось, что отрезок [a,b] – конечный, а функция f(x) ограничена на этом отрезке. При нарушении хотя бы одного из этих условий вводят обобщение определенного интеграла – несобственные интегралы.

9.1.Несобственные интегралы первого рода (по бесконечному промежутку).

9.1.1.Основные определения

9.1.2.Обобщенная формула Ньютона-Лейбница

9.1.3.Признаки сходимости интегралов с бесконечными пределами

9.1.4.Абсолютная и условная сходимость

9.2.Несобственные интегралы второго рода (от неограниченных функций)

9.2.1.Признаки сходимости несобственных интегралов от неограниченных функций

9.2.2.Примеры решения задач

9.1.Несобственные интегралы первого рода (по бесконечному промежутку)

9.1.1. Основные определения

О Пусть функция f(x) непрерывна на интервале [a, ∞). Тогда она непрерывна на любом промежутке [a,b], где b>a, и существует интеграл

∫b f (x)dx . Несобственным интегралом первого рода называется предел

a
limb→∞	∫b	f (x)dx		и	обозначается	∞∫ f (x)dx .	Таким	образом,
	a					a
∞∫ f ( x )dx = limb→∞			∫b	f ( x )dx .
a			a

Если этот предел существует и конечен, то говорят, что несобственный

Оинтеграл сходится. Если же этот предел не существует или бесконечен,

то говорят, что несобственный интеграл расходится.

Аналогично определяется несобственный интеграл и для промежутка

( −∞,b]: ∫b	f ( x )dx = alim→−∞ ∫b	f ( x )dx , если этот предел существует и коне-
−∞	a

270 Лекция 9

чен. Для функции f (x), непрерывной на промежутке ( −∞, +∞), несобствен-

ный интеграл +∞∫ f (x)dx определяется равенством:

−∞
+∞∫	f ( x )dx = ∫c	f ( x )dx + +∞∫ f ( x )dx ,
−∞	−∞	c

где с – любое число. Несобственный интеграл в левой части называется сходящимся, если сходится каждый несобственный интеграл в правой части.

9.1.2. Обобщенная формула Ньютона-Лейбница

Пусть F(x) – первообразная для функции f(x) на промежутке [a, ∞ ). Вос-

пользуемся формулой Ньютона-Лейбница для интеграла ∫b f ( x )dx .

Тогда

∞

∫

f ( x)dx = lim

∫

f ( x)dx = lim[ F(b)−F(a)] = lim F(b)−F(a).

b→+∞

Если обозначить lim F( b ) через F(+ ∞ ), то можно записать:

b→+∞

∞∫ f ( x )dx = F( +∞ ) − F( a ) = F( x )|a+∞ .

Аналогично

+∞

∫

f ( x )dx = F( x )|b−∞ ,

∫

f ( x )dx = F( x )|+∞−∞ , где F(- ∞ ) = lim F( x ) .

x→−∞

−∞

Пример:

+∞ dx

Исследовать сходимость интеграла

∫a

x p

Решение:

∞

При p ≠1 ∫

= blim→+∞ ∫x− p dx =

− p+1

−p+1

= lim

lim

−

a .

b→+∞

−p +1

−p+1b→∞

−p+1

Пусть р > 1, тогда −p +1 < 0 и

− p+1

+∞ dx

−p+1

lim b

= 0,

= −

, значит,

∫a x p

−p+1

b→+∞

при р > 1 интеграл сходится.

Пусть р < 1, тогда −p +1 > 0

и lim b− p+1 = ∞, т.е. интеграл

+∞ dx

при р < 1

∫a

x p

b→+∞

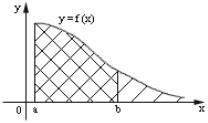
Несобственные интегралы

271

расходится.

При p =1:

∞ dx

= lim (lnx)

= lim (lnb −lna)= ∞ . Интеграл расходится.

∫a x p

b→∞

Пример:

Вычислить несобственные интегралы или доказать, что они расходятся:

+∞

∫

; 2) ∫

; 3)

∫ cos xdx ; 4) ∫ exdx ; 5)

∫

−∞

1+ x

Решение:

Воспользуемся обобщенной формулой Ньютона-Лейбница:

+∞ dx

1 ∞

∫1

= −

= −( 0

−1) =1 (интеграл сходится).

+∞ dx

∞

∫1

= ln x |

= lim ln x = ∞ (интеграл расходится).

x→∞

+∞

∫

cosxdx = sinx |+∞

= lim sinx . Этот предел

не существует, поэтому

x→+∞

+∞∫ cosxdx - расходится.

∫

ex dx = ex |−∞0

= e0 − lim ex

=1−0 =1 (интеграл сходится).

x→−∞

−∞

+∞

−∞∫

= arctgx |−∞

2 −( − 2 ) =π (интеграл сходится).

1+ x2

Выясним геометрический смысл несобст-

венного интеграла 1-го рода.

Пусть f ( x ) ≥ 0

на промежутке [a,+ ∞).

Тогда ∫b

f ( x )dx

численно равен площади фи-

гуры, ограниченной снизу отрезком [a,b] оси Ox, сверху – линией y = f (x), слева и справа –

прямыми x = a и x = b. При возрастании b прямая x = b, ограничивающая эту фигуру,

двигается вправо, а интеграл ∫b f ( x )dx стре-

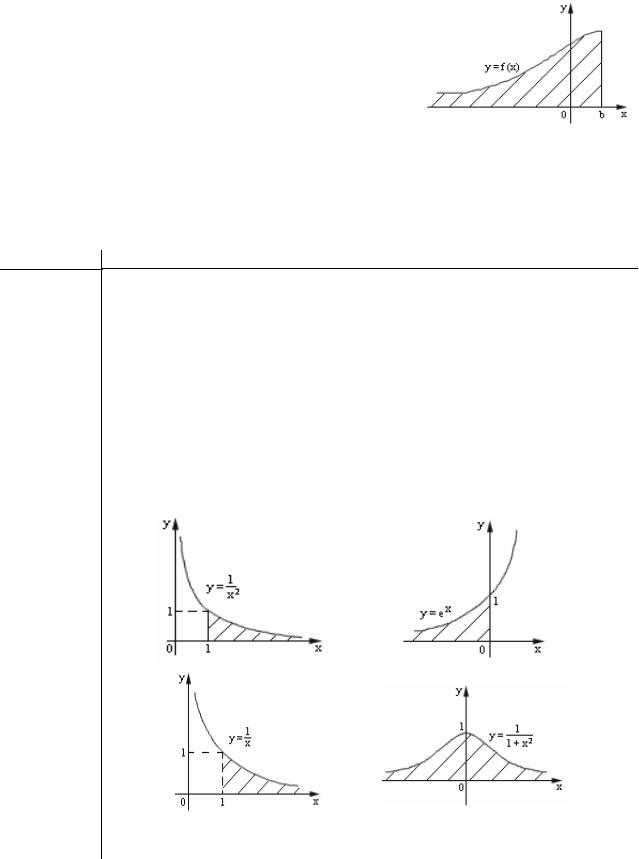
272

Лекция 9

мится к интегралу ∞∫ f ( x )dx . Поэтому величи-

ну интеграла ∞∫ f ( x )dx естественно принять за

площадь бесконечной фигуры, ограниченной снизу осью Ох, сверху графиком функции y = f (x), слева – прямой x = a.

Аналогично ∫b	f ( x )dx для случая f(x) ≥0 чис-
−∞

ленно равен площади бесконечной фигуры, ограниченной снизу осью Oх, сверху кривой y = f (x), справа прямой x=b.

Пример:

Вычислить площади бесконечных фигур, ограниченных осью Ох, линией y = f(x), прямой x = a, если

а) f (x)=		1	, a = 1,		x ≥1;
а) f (x)=		x2	, a = 1,		x ≥1;
		x2
б)	f (x)=	1	, a=1,		x ≥1;
б)	f (x)=	x	, a=1,		x ≥1;
		x
в)	f (x)= ex , a=0, x ≤ 0 ;
г) f (x)=		1		, x (−∞, +∞) .
г) f (x)=		1+ x2		, x (−∞, +∞) .
Решение:		1+ x2
Решение:
Построим фигуры, ограниченные данными линиями
					А	В

Воспользуемся результатами примера 1.

Несобственные интегралы			273

	+∞	+∞
	а) S = ∫1 dxx2 =1; б) S = ∫1 dxx = ∞ ;
	Фигура, изображенная на рис.б), имеет бесконечную площадь.
	0	+∞	dx
	в) S = ∫ ex dx =1; г) S = ∫		dx	=π .
	в) S = ∫ ex dx =1; г) S = ∫		2	=π .
	−∞	−∞	1+ x

9.1.3. Признаки сходимости интегралов с бесконечными пределами

Признаки сравнения

1. Пусть при а ≤ х < +∞, 0 ≤ f(х) ≥ g(х). Если +∞∫ g(x)dx сходится, то сходит-

			a
ся и +∞∫	f (x)dx , причем +∞∫	f (x)dx ≤ ∞∫g (x)dx . Если расходится +∞∫ f (x)dx ,
a	a	a	a

то расходится и +∞∫ g (x)dx .

2.Если при а ≤ х < +∞, f(х) > 0, g(х) > 0 и существует конечный предел

lim

f (x)

≠ 0 , то интегралы

+∞ f (x)dx ,

+∞ g (x)dx сходятся или расходят-

x→+∞

g (x)

∫

ся одновременно.

9.1.4. Абсолютная и условная сходимость

Если сходится

+∞∫

f (x)

dx ,

то сходится и∞∫ f (x)dx . В этом случае

∞∫ f (x)dx называется абсолютно сходящимся.

Если ∞∫ f (x)dx сходится, а +∞∫

f (x)

dx расходится, то ∞∫ f (x)dx называется

условно сходящимся.

Из первого признака сравнения можно получить следующее утверждение.

274

Лекция 9

ТЕсли при х → + ∞ функция f(х) > 0 является бесконечно малой порядка

α по сравнению	1	, то интеграл	+∞∫	f (x)	dx сходится при α > 1 и расхо-
α по сравнению	1	, то интеграл	+∞∫	f (x)	dx сходится при α > 1 и расхо-
	x
	x		a
дится при α ≤ 1.

Признак сходимости Абеля

Пусть f(х) >0 и g(х) определены и ограничены при а ≤ х < +∞, причем

∞∫ f (x)dx сходится;

2) g(х) монотонна и ограничена,

g( x )

≤k =const .

Тогда сходится и интеграл ∞∫ f (x)g (x)dx .

Пример:

Вычислить +∞∫ e−3x dx .

Решение:

Имеем

+∞

e−3x dx =

lim

e−3x dx =

lim

−

1 e−3x

= 1 lim

1−e−3b

1 .

b→+∞

(

)

∫

b→+∞ ∫

b→+∞

Несобственный интеграл сходится.

Пример:

−1

dxx2 .

Вычислить −∞∫

Решение:

−1

−1 dx

∫

alim→−∞ ∫

= alim→−∞ −

alim→−∞

= 1, т.е. предел существу-

−∞

ет. Следовательно, искомый несобственный интеграл сходится.

Пример:

+∞

Исследовать на сходимость интеграл

∫2

x ln2 x

Решение:

∞

∫

= blim→∞

∫

−

= blim→∞

2 x ln

x ln

ln x

ln 2

т.е. несобственный интеграл сходится.

Пример:

Несобственные интегралы

275

Исследовать на сходимость интеграл +∞∫ (x +31)dx .

Решение:

x +1

∞

Имеем: (

3 ) ≥

, ∫

= ∫

расходится (здесь р =

< 1).

x 2

Следовательно, по признаку сравнения расходится и исходный интеграл.

9.2.Несобственные интегралы второго рода (от неограниченных функций)

О Пусть функция f (x) непрерывна на ин-

тервале [a,b) и неограниченна вблизи b. Тогда функция непрерывна на любом отрезке [a,b1], где а≤ b1<b и, следовательно,

существует интеграл ∫ f (x)dx .

Рассмотрим lim ∫ f (x)dx . Этот предел называется несобственным ин-

b1→b−0 a

тегралом второго рода и обозначается

∫b f (x)dx . Таким образом,

b		b1
∫ f (x)dx = bli→mb−0		∫ f (x)dx .
a	1	a

Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае несобственный интеграл называется расходящимся.

Аналогично для функции f(x), непрерывной на промежутке (a,b] и неог-

раниченной вблизи а, несобственный интеграл ∫b f (x)dx определяется

следующим образом:

b		b
∫	f ( x)dx = a lim→a+0 ∫ f ( x)dx .
a	1	a1

Если этот правосторонний предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходя-

щимся.

276						Лекция 9
Пусть теперь функция			f (x)			непрерывна на отрезке [a,b] всюду, кроме
некоторой точки c (a<c<b), и неограниченна
вблизи с.
Несобственный интеграл ∫b					f (x)dx определя-
ется равенством:				a
ется равенством:
∫b	f (x)dx = ∫c	f (x)dx + ∫b				f (x)dx .
a	a				c
Если каждый из интегралов в правой части равенства сходится, то не-
собственный интеграл			∫b	f (x)dx называется сходящимся, в противном
			a

случае – расходящимся.

Пусть F (x) – первообразная для функции f (x) на промежутке [a,b) и f (x) не ограничена вблизи b.

	b			b1
Тогда	∫	f (x)dx = lim		∫	f (x)dx = lim [F (b1 ) − F (a)] = lim F (b1 ) − F (a) .
	∫	b1	→b−0	∫	b1→b−0	b1→b−0
	a			a	F(b1) через F(b), то получим следующий аналог
Если обозначить			lim		F(b1) через F(b), то получим следующий аналог
			b1→b−0

формулы Ньютона-Лейбница для несобственного интеграла второго рода:

b
∫	f (x)dx = F (b) − F (a) = F (x) \|b			, где F(b)= lim F (x) .
∫			a		x→b−0
a				f (x), не ограниченной вблизи а,
Аналогично		для	функции	f (x), не ограниченной вблизи а,
b
∫	f (x)dx = F (x) \|b , где F (a) = lim				F ( x) .
∫		a	x→a +		0
a

Пример:

Вычислить несобственные интегралы или доказать, что они расходятся:

1) ∫2	dx		; 2)	∫1	dx .
1) ∫2			; 2)	∫1	dx .
0	2 − x			−1	x
Решение:						1
В первом интеграле подынтегральная функция f (x)=						1	не ограни-
В первом интеграле подынтегральная функция f (x)=						2 − x	не ограни-
						2 − x
чена при x=2, поэтому интеграл ∫2		dx		является несобственным. При-
чена при x=2, поэтому интеграл ∫2		2 − x		является несобственным. При-
	0	2 − x

меним обобщенную формулу Ньютона-Лейбница:

Несобственные интегралы

277

d (2 − x)

∫

= −∫

= −2 2 − x |0

= −(0 −2 2) = 2 2 .

2 − x

Во втором интеграле подынтегральная функция f(x)=

не ограничена

вблизи x=0. Поэтому, по определению, ∫1

= ∫0

+ ∫1

−1

−1 x

0 x

Рассмотрим интеграл

∫0

dx = ln

0−1 = ∞ .

Этот интеграл расходится, по-

−1

этому и интеграл ∫1 dx - расходится.

−1 x

Отметим, что если бы мы стали вычислять данный интеграл, не обращая внимания на разрыв подынтегральной функции в точке x = 0, то получи-

	ли бы неверный результат ∫1	dx = ln	x	1−1 = 0 , что неверно.

	−1	x

Рассмотрим геометрический смысл несобственного интеграла 2-го рода.
Пусть f (x)	≥ 0 и f (x) – непрерывна на [a,b) и не ограничена вблизи b. То-
b1
гда ∫ f (x)dx	(b1 < b) равен площади фигуры, ограниченной снизу отрезком

[a,b1] оси Ох, сверху – линией y = f (x), слева и справа – прямыми x=a, x=b1.

При стремлении b1 к b, прямая x=b1 cтремится к прямой x=b.			Поэтому
	b1	b
blim→b−0 ∫ f (x)dx = ∫ f (x)dx естественно принять за площадь бесконечной фигу-
1	a	a
			(x), слева
ры, ограниченной снизу отрезком [a,b] оси Ох, сверху линией y = f

и справа – прямыми x = a и x = b.

9.2.1. Признаки сходимости несобственных интегралов от неограниченных функций

Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны признакам сходимости интегралов с бесконечными пределами. Эталоном сравнения служит интеграл

b	dx
∫			, (β > 0),
	(b −x)	β
a

который сходится при β < 1 и расходится при β ≥ 1.

278

Лекция 9

Пример:

Исследовать на сходимость интеграл ∫

ln x

Решение:

При х → 1

- эквивалентные бесконечные большие, т.к.

ln x

−1)

по

(

x −1

ln x

lim

= lim

)

правилу

= lim

= 1, интеграл

(

x→1 1

x→1 ln x

x→1

Лопиталя

x −1

β =1. Следовательно,

∫

расходится при

∫

расходится.

(x −1)

ln x

9.2.2. Примеры решения задач

Пример:
Исследовать сходимость интеграла ∫1		cos2 x			dx .
Исследовать сходимость интеграла ∫1		(	− x2	)	dx .
0	3	1	− x2

Решение:

Подынтегральная функция неограниченно возрастает при х → 1, представим подынтегральную функцию в виде

f (x) =	cos2 x	1	=	cos2 x	1	.
					(1− x)13
	3 1+ x	3 1− x		3 1+ x

Первый сомножитель особенности при х → 1 не даёт, а следовательно, сравнение с (x1−1) при х → 1 даёт α = 13 < 1. Следовательно, интеграл

сходится.

Пример:

Вычислить (или установить расходимость) +∞∫ cos xdx .

							π 2
Решение:
По определению,
+∞		B				B
	cos xdx = lim		cos xdx = lim		sin x		= lim (sin B −1) = −1+ lim sin B .
	cos xdx = lim		cos xdx = lim		sin x		= lim (sin B −1) = −1+ lim sin B .
∫		B→+∞ ∫	B→+∞	(		π 2 )	B→+∞	B→+∞
∫		B→+∞ ∫	B→+∞	(		π 2 )	B→+∞	B→+∞
π 2		π 2
Так как		lim sin B не существует, то исследуемый несобственный инте-
		B→+∞

грал расходится.

1+ x2

Несобственные интегралы

279

Пример:

+∞

Исследовать на сходимость

∫3

x3 + 2x + 2

Решение:

Рассмотрим f (x) =

. Наибольшая степень многочлена в зна-

x3 + 2x + 2

менателе равна 3. Поэтому для сравнения возьмем функцию g (х) =

f (x)

x 3

тогда

lim

= 1 ≠ 0 и по предельному признаку

x→∞ g (x)

x→+∞ x3 + 2x + 2

сравнения исследуемый несобственный интеграл и интеграл +∞∫ g (x)

dx =

+∞

= ∫3 dxx3

сходятся или расходятся одновременно. Последний интеграл схо-

дится (р > 1), следовательно, исследуемый интеграл тоже сходится.

Пример:

+∞ cos 2xdx

Исследовать на абсолютную сходимость интеграл ∫ .

Решение:

Здесь f (x) =	cos 2x	; f (х) =	cos 2x	=	cos 2x	, так как для любых х

	1+ x2		1+ x2		1+ x2

сos 2х ≤ 1, то f (х) ≤ 1+1x2 = g(х).

Рассмотрим

+∞ g (x)dx = +∞

= lim

arctg x

= lim arctg b − lim arctg1=

1+ x

b→+∞

(

1 )

b→+∞

∫

= π

+∞

−

, следовательно,

∫ g (x)dx сходится.

+∞

Тогда по признаку сравнения сходится интеграл ∫ f (x) dx , а исследуе-

мый интеграл сходится абсолютно.

Пример:

Вычислить (или установить расходимость) ∫1

1− x

Решение:

Функция

f (x) =

непрерывна для х [0, 1) и lim f (x)= +∞ .

− x2

x→1−0

1−ε

= εlim→+0 (arcsin

10−ε )=

Тогда ∫

= lim

∫

1− x2

ε→+0

280					Лекция 9

	= lim arcsin (1−ε ) −arcsin 0 =	π	− 0 =	π	, т.е. интеграл сходится.
	ε→+0	2		2

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

понятие несобственного интеграла первого и второго рода,

признаки сходимости несобственных интегралов.

Студент должен уметь:

исследовать несобственные интегралы на сходимость.

Лекции 10 - 11 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Дифференциальные уравнения, содержащие неизвестную функцию, ее производные и известные функции независимого аргумента, начали исследоваться одновременно с возникновением дифференциального и интегрального исчислений. Важность таких уравнений обусловлена тем, что в очень большом количестве случаев законы природы, управляющие теми или иными процессами, выражаются в форме дифференциальных уравнений, а расчет течения этих процессов сводится к решению дифференциального уравнения.

10.1.Основные понятия

10.2.Дифференциальные уравнения первого порядка (ДУ-I)

10.2.1.ДУ с разделяющимися переменными

10.2.2.Однородные ДУ первого порядка

10.2.3.Обобщенные однородные ДУ первого порядка

10.2.4.Линейные ДУ первого порядка

10.2.5.Уравнение Бернулли

10.2.6.Уравнение в полных дифференциалах

10.2.7.Таблица 1. Решения ДУ первого порядка

10.2.8.Особые решения ДУ первого порядка

11.1.ДУ высших порядков

11.2.ДУ второго порядка (ДУ-II)

11.3.Некоторые типы ДУ второго порядка, приводимые к ДУ первого порядка

11.3.1.ДУ y′′ = f ( x)

11.3.2.ДУ вида y′′ = f (x, y′)

11.3.3.ДУ y′′ = f (y, y′)

11.4.Таблица 2. Решения ДУ второго порядка, допускающих понижение порядка

11.5.ДУ n - го порядка, допускающие понижение порядка

11.5.1.ДУ вида y(n) = f ( x)

11.5.2.ДУ вида F (y, y ', y ",..., y(n) )= 0

11.5.3.ДУ вида F (x, y(k ),..., y(n) )= 0 .

11.5.4.ДУ вида dxd G (x, y, y ',..., y(n−1) (x))= 0 .

10.1.Основные понятия

ОДифференциальным уравнением (ДУ) называется уравнение, связы-

вающее между собой независимую переменную х, искомую функцию

y = f (x) и ее производные y′, y′′,...y( n ) .

282	Лекции 10 - 11

Например, скорость тела v , движущегося под действием силы F, может быть найдена из второго закона Ньютона, т.е. из ДУ m dvdt = F , где m - масса тела,

t - время.

ДУ с одной независимой переменной называется обыкновенным.

ОПорядок наивысшей производной, входящей в уравнение, называется порядком ДУ.

Общий вид ДУ n-го порядка:

F( x, y, y′, y′′,...y( n ) ) = 0 .

Например, 1. y′+ 2x y = sinx , 2. y′′′+ yy′ = 0 .

Решением или интегралом ДУ называется всякая функция y = f ( x ) ,

которая, будучи подставлена в ДУ, превращает его в тождество. График решения называется интегральной кривой.

Основная задача интегрального исчисления заключается в нахождении решения ДУ y′ = f ( x ) , т.е. y = ∫ f ( x )dx + c .

Пример:
Найдите решение ДУ y′′ = 0 .
Решение:								= ∫c1dx + c2
y	′′	′ ′	= 0 → y	′	= c1	,	y		= c1 x + c2 .
y		= ( y )	= 0 → y		= c1	,	y		= c1 x + c2 .

О Общим решением ДУ F( x, y, y′,..., y( n ) ) = 0 называется такое решение y = f ( x,c1 ,c2 ,...,cn ) , которое содержит столько независимых произвольных постоянных ci , i =1,2,...n , каков порядок этого ДУ.

ОЕсли общее решение задано в неявном виде Φ( x,y,c1 ,c2 ,...,cn ) = 0 , оно называется общим интегралом ДУ.

ОВсякое решение ДУ, которое получается из общего при определенных значениях произвольных постоянных, называется частным решением этого ДУ.

Пример:

Найдите решение ДУ y′′+ y = 0 .
Решение:		′′
′′	= −sinx ,		= −cosx , функция вида	y = c1sinx +c2cosx ;
Так как (sinx)		(cosx)
будет удовлетворять уравнению.
Если c1 = 2 ,	c2 = 5 ,	то y1 = 2sinx +5cosx ; если c1 = 0 , c2 = −4 , то
y2 = −4cosx .

Дифференциальные уравнения

283

10.2. Дифференциальные уравнения первого порядка

Рассмотрим ДУ вида F( x, y, y′) = 0 или y′ =ϕ( x, y ). Общим решением является y = f ( x,c ) . Геометрически решение представляет собой однопараметрическое семейство кривых. Значение y′ в точке M ( x, y ): y′ = tg α .

yС3 С2 С1

M ( x, y)

ОЗадача Коши для ДУ формулируется следующим образом: найти решение y = f ( x ) ДУ y′ =ϕ( x, y ), удовлетворяющее начальному условию: y0 = f ( x0 ).

Геометрически задача Коши заключается в нахождении частного решения ДУ, проходящего через заданную точку с координа-

тами ( x0 ,y0 ) .

Общее решение y = f ( x,c ) становится ча-

стным y = f ( x,c0 ) , если y0 = f ( x0 ,c ) , от-

куда можно найти c = c0 .

M ( x0 , y0 ) y0

ТТеорема Коши (теорема существования и единственности решения ДУ первого порядка, разрешенного относительно производной). Если функция ϕ( x, y ) непрерывна в области, содержащей точку ( x0 ,y0 ) , то су-

ществует функция y = f ( x ) , удовлетворяющая уравнению y′ =ϕ( x, y ) и обращающаяся в y0 при x = x0 .

Если, кроме того, непрерывна и частная производная ϕ′y ( x,y ) , то реше-

ние будет единственным.

10.2.1. ДУ с разделяющимися переменными

ДУ y′ =ϕ( x, y ) удобно записать в виде:

dydx = Q(P( x,yx,y )) или P( x, y )dx −Q( x, y )dy = 0 .

О ДУ X ( x )Y ( y )dx + X1( x )Y1( y )dy = 0 называется ДУ с разделяющимися

переменными.

Разделим уравнение на Y ( y ) X1( x ) ≠ 0 , тогда X ( x ) dx + Y1( y ) dy = 0 .

X1( x ) Y ( y )

Обозначим входящие в это уравнение функции через P( x ) и Q( y ) , то-

гда получим ДУ P( x )dx + Q( y )dy = 0 с разделенными переменными.

284	Лекции 10 - 11
Считая y	функцией x , перепишем уравнение в виде P( x )dx = −Q(y)dy , т.е.

в виде равенства дифференциалов двух функций одного аргумента. Известно, что если дифференциалы функций равны, то сами функции отличаются на константу, т.е., общий интеграл этого ДУ имеет вид:

∫P( x )dx + ∫Q( y )dy = c .

Пример:

Найдите решение ДУ y′ = xy .

Решение:

dy y								±y =\| cx \| y	C = 2
dx	=		,	xdy = ydx , умножая уравнение на
		x							C = 1
1	, последовательно получаем				dy	= dx	,	0	x
xy					y
						x

∫dyy = ∫dxx , ln y = ln x +ln c , где постоянная

интегрирования представлена в логарифмической форме, значит, ln | y |= ln | cx |, | y |=| cx |, x ≠ 0 .

10.2.2. Однородные ДУ первого порядка

ОФункция F( x, y ) называется однородной функцией n-го порядка, если для любого числа k имеет место тождество F( kx,ky ) ≡ k n F( x, y ) .

Например, если

F( x,y ) = 3

x3 + y3 , то

F( kx,ky ) = 3 ( kx )3 +( ky )3 =

= k 3

x3 + y3 , значит, F( x, y ) является однородной функцией первого по-

рядка. Функция F( x, y ) = ex−y

не является однородной.

ДУ

y′ =

f ( x, y )

называется

однородным

относительно х

и у,

если

f ( x, y )

есть однородная

функция

нулевого

порядка,

то

есть

f ( kx,ky ) = f ( x, y ).

Решим однородное уравнение

= f ( x,y ) .

Преобразуем функцию f (x, y) к виду f (x, y) = f 1,

, считая k =

. Решаем

= u x ,

ДУ

f 1,

. Сделаем подстановку u =

, тогда

= u +

Дифференциальные уравнения

285

и уравнение примет вид: u + x

= f (1,u ) - ДУ с разделяющимися перемен-

ными. x

= f (1,u ) −u ,

∫

+ c .

f (1,u ) −u

Пример:

Найдите решение ДУ y′

+1 .

Решение:

Это ДУ является однородным, т.к. правая часть есть функция только от-

ношения

Положим

= u , y = ux , тогда

′

= u x +u и уравнение принимает вид:

′

+ln

, lnu = cx ,

u x + u = u (lnu +1), u x =ulnu , ulnu

= x , ln

lnu

= ln

откуда u = ecx , значит,

y = xecx .

10.2.3. Обобщенные однородные ДУ первого порядка

a1 x + b1 y + c1

ДУ вида

y′ = f

называется обобщенным однородным

a2 x + b2 y + c2

ДУ первого порядка и решается путем сведения к однородному ДУ преобразованием параллельного переноса координат с помощью замены переменных

x = X +α,	a α + b β + c = 0,
	при условии, что 1	1	1
y = Y + β ,	a2α + b2 β + c2 = 0.

Проиллюстрируем решение обобщенных однородных ДУ первого порядка на примере. Найдем общий интеграл дифференциального уравнения

y′ =	y + 2
		.
	2x + y − 4

Сведение к однородному достигается преобразованием параллельного пере-


носа системы координат,				x = X +α , y =Y + β .
При этом	dy	=	d(Y + β )	=	dY		, и в новых переменных уравнение принимает
При этом	dx	=	d( X +α )	=	dX		, и в новых переменных уравнение принимает
	dx		d( X +α )		dX
вид:				dY			Y +( β + 2 )
				dY		=	Y +( β + 2 )	.
						=	2 X +Y +( 2α + β − 4 )	.
				dX			2 X +Y +( 2α + β − 4 )

286	Лекции 10 - 11
Выбирая постоянные α и β из условия β + 2 = 0,
2α + β − 4 = 0,

получаем α = 3, β = −2 ; т.е. искомое преобразование переменных имеет вид:

x = X + 3 , y = Y − 2 ,

а уравнение упрощается

dY	=	Y	.	(1)
dX		2 X +Y

Поделив числитель и знаменатель в правой части на Х (при однородное уравнение

dY	=	Y X	, при X ≠ 0 .
dX		2 +Y X

Используя подстановку Y X = u( x ), получаем

X	du	=	−u2 −u	.
	dX		2 + u

Разделяя переменные, приходим к уравнению:

2 + u	du = −	dX	; ( u ≠ 0 , u ≠ −1, X ≠ 0 ).
u2 + u		X

Интегрируя, находим общий интеграл в форме:

X ≠ 0 ), получаем

(2)

(3)

	2 +u	du =		(1 +u )2 −u du 2ln \| u \| −ln \|1+u \| +ln \| X \|= C ,

∫u2 +u			∫	u2 +u	1

( u ≠ 0,u ≠ −1,X ≠ 0 ).

Случай X = 0 следует проверить подстановкой в уравнение (1), а случаи u = 0 и u = −1 - подстановкой в уравнение (3), поскольку возможна потеря решений. Находим, что X = 0 не является, а u = 0 и u = −1 являются решениями уравнения (1).

Таким образом, уравнение (3) имеет следующие решения:
2ln \|u \| −ln \|1 + u \| +ln \| X \|= C1 (общий интеграл),	(4а)
u = 0 ,	(4б)

Дифференциальные уравнения

287

u = −1 (частные решения).

Возвращаясь к старым переменным, получаем:

2ln

y + 2

− ln

1 +

y + 2

+ ln | x −3|= C ,

x −3

y + 2 = 0 ,

y + 2

= −1.

x −3

После упрощения общий интеграл (5а) принимает вид:

2ln | y + 2 | −ln | x + y −1|= C .

Ответ: общий интеграл имеет вид: 2ln | y + 2 | −ln | x + y −1|= C . Замечание: общий интеграл (6) можно представить также в форме:

(4в)

(5а)

(5б) (5в)

(6)

ln	( y + 2 )2	= C	или	( y + 2 )2	= C	2	, C	2	= ±eC1 .

	x + y −1	1		x + y −1

Тогда частные решения (5б) и (5в) получаются при C2 = 0 и C2 = ∞ соответственно.

10.2.4. Линейные ДУ первого порядка

ОЛинейным ДУ первого порядка называется уравнение, линейное отно-

сительно

неизвестной

функции

ее

производной

y′:

y′+ P( x )y = Q( x ), где P( x ), Q( x ) – непрерывные функции.

Ищем решение в виде произведения двух функций y = u( x ) υ( x ), одна

из которых считается произвольной (υ ), а другая находится из уравнения.

Если y = u υ ,

′

dυ

то

= uυ

, то есть

= u dx +

υ dx

и уравнение прини-

+υu

мает вид:

dυ

+υ

+ Puυ = Q , u

+ Pυ

+υ

= Q .

(*)

dυ

В силу произвольности выберем υ такой,

что

+Pυ=0, тогда

= −Pdx ,

ln υ = −∫Pdx + lnc1 , значит υ = c1e−∫Pdx .

288	Лекции 10 - 11

Положим c1 =1, получим υ = e−∫Pdx . Подставляя полученное для υ выражение в ДУ (*), найдем u :

υ( x ) dudx = Q( x ) , dudx = Q(υ( xx)) , u = ∫Qυ((xx)) dx + c .

Витоге общее решение имеет вид:

y =υ(x)

Q(x) dx + c .

∫υ(x)

Пример:

Найдите решение ДУ

−

y = ( x +1)3 , x ≠ −1.

x +

Решение:

dυ

Полагая y = uυ , получим, что

= u

υ ,

dυ

υ −

uυ = ( x +

, u

−

+υ

= ( x +1)

x +1

Найдем

υ из ДУ

dυ

−

υ = 0 ,

dυ

2dx

= 2 ln

x +1

откуда υ = ( x +1)2 .

x +1

Найдем u из ДУ:

( x +1)2 du

= ( x +1)3

= ( x +1) ,

u =

(x +1)2

+ c .

Общее решение примет вид:

y =

( x +1)4

+ c(x +1)2 .

10.2.5. Уравнение Бернулли

ОДУ dydx + P(x) y = Q(x) yn , где P(x) , Q(x) – непрерывные функции или постоянные, называется уравнением Бернулли.

При n = 0 оно линейное,	при n =1 с разделяющимися переменными.
Считаем, что n ≠ 0, 1. Разделим ДУ на yn , получим y−n dy + Py−n+1		= Q .
	dx
Сделаем замену переменной	z = y−n+1 , тогда получим dz = (−n	+1) y−n dy	,
	dx	dx

dxdz + (−n +1)Pz = (−n +1)Q - линейное уравнение.

Пример:

Найдите решение ДУ dydx + xy = x3 y3 .

Решение:

Дифференциальные уравнения

289

Здесь P(x) = x ,

Q(x) = x3 ,

n = 3 .

, получим y

−3

′

+ xy

−2

= x

Умножив уравнение на

Заменяя z = y−n+1 = y−2 , получаем dz

= −2 y−3 dy

−2xz = −2x3 .

Полагая

z = uυ ,

= u dυ + du υ

u dυ + du

υ −2xuυ = −2x3

dυ

−2xυ

= −2x

приходим

линейному ДУ для

+υ

υ :

dυ

−2xυ = 0 ,

dυ

= 2xdx , откуда ln

= x2 ,υ = ex2 .

Тогда уравнение для u принимает вид:

ex2 du

= −2x3 , du = −2e−x2 x3dx ,

откуда u = −2∫e−x2 x3dx =(по частям)= = x2e−x2 +e−x2 +c ,

z = uυ = x2 +1+ cex2 , y−2 = x2 +1+cex2 , y =

x2 +1+cex2

Заметим, что уравнение Бернулли можно решить как линейное, сразу сделав замену y = uυ .

10.2.6. Уравнение в полных дифференциалах*)

ОУравнение P(x, y)dx + Q(x, y)dy = 0 называется уравнением в полных дифференциалах, если P(x, y) и Q(x, y) – непрерывные дифференци-

руемые функции, для которых ∂∂Py = ∂∂Qx , причем ∂∂Py и ∂∂Qx непрерывны

в некоторой области.

ТДля того чтобы выражение Pdx + Qdy было полным дифференциалом некоторой функции двух переменных u(x, y) , необходимо и достаточно, чтобы ∂∂Py = ∂∂Qx .

Докажем необходимость этого условия.

Пусть du = Pdx + Qdy , тогда по определению дифференциала функции

двух переменных P =

∂u

, Q =

∂u

. Вычислим

∂P

∂2u

∂Q

∂2u

∂x

∂y

∂y∂x

∂x

∂x∂y

Известно, что вторые смешанные производные функции двух переменных равны друг другу, если они непрерывны.

290										Лекции 10 - 11
Так как			∂P	и	∂Q	непрерывны по условию:	∂2u	=	∂2u	, следователь-
Так как			∂y	и	∂x	непрерывны по условию:	∂x∂y	=	∂y∂x	, следователь-
			∂y		∂x		∂x∂y		∂y∂x
но,	∂P	=	∂Q	и	Pdx + Qdy = 0 , du = 0 , откуда u(x, y) = c .
	∂y		∂x

Основываясь на вышеизложенном, решим ДУ в полных дифференциалах.

Пример:

Решить ДУ		2x		dx +		y2 −3x2		dy = 0 .
		y3				y4

Решение:
Здесь P =	2x		,	Q =	y2 −3x2		.
	y3					y4

1). Проверим, является ли полным дифференциалом выражение, стоящее

в левой части ДУ. Вычислим

∂P

= −

∂Q

= −

6x .

∂y

∂x

∂P

∂Q

−3x2

Видим, что

, значит,

dx +

dy = du .

∂y

∂x

2). Так как выражение, стоящее в левой части уравнения, является пол-

∂u

∂x

ным дифференциалом, значит, du =

dx +

∂x

∂y

, и

∂u

−3x2

∂y

3). Интегрируя первое из уравнений системы, получаем:

u(x, y) = ∫ y3

dx +ϕ( y) =

+ϕ( y) , где постоянная интегрирования по x

представляет собой функцию ϕ( y) .

4). Для нахождения ϕ( y)

продифференцируем по

полученное для

∂u

3x2

′

u(x, y) выражение: ∂y = −

+ϕ ( y) .

−3x2

3x2

′

5). Второе уравнение системы дает:

= −

+ϕ ( y) ,

′

откуда ϕ ( y)

, ϕ( y) = −

+c1 , значит, u(x, y)

−

+c1

и общим

интегралом ДУ является выражение

−

= c .

Дифференциальные уравнения

291

10.2.7. Таблица 1. Решение ДУ первого порядка

Вид уравнения

Тип уравнения

Метод решения

1. P(x)dx +Q( y)dy = 0

с разделяющимися

непосредственное

переменными

интегрирование

, y = u x ,

y′ = f

однородное

y′ = u′ x + u

x = X +α,

a1x + b1 y + c1

y =Y + β;

обобщенное

a α + b β + c = 0,

y′ = f

однородное

a α

+ b

β + c = 0;

a2 x + b2 y + c2

y′ =Y′ = dX

y′ = P(x) y + Q(x)

линейное по y(x)

y = u υ

′

= uυ

′

+ u υ

′

линейное по x( y)

x = u υ

′

x = P( y)x + Q( y)

′

= u υ +uυ

y′+ P(x) y = Q(x) yn

Бернулли

y = u υ

интегрирование

7. P( x, y)dx + Q( x, y)dy = 0

системы

∂P

= ∂Q

уравнение в полных

∂u

= P(x, y),

∂x

∂y

∂x

дифференциалах

du(x, y) = 0

∂u

= Q(x, y)

∂y

292	Лекции 10 - 11
10.2.8. Особые решения ДУ первого порядка
Если ДУ первого порядка не разрешено относительно производной, т.е.
имеет вид F(x, y, y ) = 0 , то через некоторые точки плоскости (x, y)	может про-
′

ходить не одна интегральная кривая, т.е. для некоторых начальных значений может нарушиться единственность решения.

	Линия L называется огибающей однопа-			y
О
	раметрического	семейства	линий

	Φ(x, y,c) = 0 , если она в каждой точке каса-			x
	ется той или иной линии семейства, причем
				0

в различных точках линии L ее касаются различные линии данного семейства.

Для определения огибающей служат следующие два уравнения:

Φ(x, y,c) = 0,Φc′(x, y,c) = 0.

Пусть ДУ F (x, y, y′) = 0 (*) имеет общий интеграл Φ(x, y,c) = 0 (**).

Если это семейство интегральных кривых имеет огибающую, то огибающая также является интегральной кривой ДУ.

Φ(x, y,c) = 0,

Уравнения после исключения параметра c , определяют

Φc′(x, y,c) = 0,

функцию y =ψ(x) .

Если эта функция удовлетворяет ДУ (*) и не принадлежит семейству (**), то она называется особым решением ДУ. В каждой точке особого решения нарушается единственность решения.

Пример:

(1+ y′2 )= R2 .

Решите ДУ y2

Решение:

− y2

ydy

= dx , (x −c)

= ±∫

ydy

= ±

− y

Вычислим

1 ∫

2 ydy

= R2 − y2 = t

= −

∫

R − y

dt = −2 ydy

1 t 2

= −

∫t−

dt = −

= − t

= − R2 − y2 .

Дифференциальные уравнения							293
Итак, x − c = ±				R2		− y2 ,	(x − c)2 = R2 − y2 .
Значит, Φ( x, y,c ) = (x − c)2 + y2 − R2 = 0 , 2( x − c )( −1) = 0 ,
	2		2		2
( x − c )		+ y		= R		y2	= R2 , откуда y = ±R , y1 = R, y2 = −R .
x = c

Итак, y = ±R – огибающие, которые удовлетворяют ДУ, являются особыми решениями.

11.1. ДУ высших порядков y( n ) = f (x,y,y′,...,y( n −1 ) )

Задача Коши заключается в нахождении решения ДУ n-го порядка, удовлетворяющего заданным начальным условиям:

y(x0 )= y0 ,
y′(x0 )= y0′ ,
	#
	#	(x0 )
	(n−1)		(n−1)	.
y			= y0	.

ТТеорема Коши (существования и единственности решения ДУ n-го по-

рядка). Если в ДУ y( n ) = f (x, y, y′,..., y( n−1 ) ) функция f (x, y, y′,..., y )( n−1 )

	и ее частные производные по аргументам	y, y′,..., y( n−1 ) непрерывны в
	некоторой области, содержащей значения	x = x0 , y = y0 , y′ = y0′, ….,
	y( n−1 ) = y0( n−1 ) , то существует и притом единственное решение		y = y( x )
		′	′
	ДУ, удовлетворяющее начальным условиям: y( x0 ) = y0 , y ( x0		) = y0 , …,
	y( n−1 ) ( x0 ) = y0( n−1 ) .
	Общим решением ДУ n-го порядка называется		функция
О	Общим решением ДУ n-го порядка называется		функция
	y =ϕ( x,c1 ,c2 ,...,cn ), которая удовлетворяет ДУ при любых значениях

	постоянных.

Частное решение ДУ (решение задачи Коши) может быть найдено из общего решения ДУ по заданным начальным условиям y( x0 ) = y0 ,

294															Лекции 10 - 11
′	′	, ….,	y	( n−1 )	( x0		( n−1 )			, из которых получаем систему уравнений:
y ( x0	) = y0	, ….,	y		( x0	) = y0				, из которых получаем систему уравнений:
						y(x		0	, c0		,...c0 )= y			0	,
								0	1			n		0
						y′(x0 , c10 ,...cn0 )= y0′ ,
									.			.	.
						.			.			.	.
						y(n−1) (x					0	, c0 ,...c0 )			= y(n−1)
											0	1	n		0
для определения постоянных c0 ,c0											,....c0 .
								1		2		n

Решение задачи Коши для ДУ n-го порядка имеет вид:

y=ϕ( x,c10 ,c20 ,...,cn0 ).

11.2.ДУ второго порядка

Решением ДУ y′′ = f ( x, y, y′) является функция y =ϕ( x,c1 ,c2 ) , пред-

ставляющая совокупность интегральных кривых.

Задача Коши заключается и нахождении решения ДУ, проходящего через точку M 0 (x0 , y0 ): y (x0 ) = y0 в заданном направлении: tgα0 = y′(x0 ) = y0′ .

11.3.Некоторые типы ДУ второго порядка, приводимые к ДУ первого порядка

11.3.1. ДУ y′′ =	f ( x )
Двукратное интегрирование дает:
	y′ = ∫ f ( x )dx + c1 , y = ∫(∫ f ( x )dx)dx + c1 x + c2 .
11.3.2. ДУ вида y′′ =			f ( x, y′)
Уравнение	d 2 y			dy	явно не содержит y(x). Сделаем замену пере-
	dx	2	= f x,
				dx

менной: p(x) =	dy	, тогда	dp	=	d 2 y	и уравнение принимает вид	dp	= f ( x, p ),
	dx		dx		dx2		dx

откуда p = p (x,c1 ), y = ∫ p (x,c1 )dx + c2 .

Дифференциальные уравнения

295

Пример:

Решите уравнение xy′′ = 2x − y′, если при x =1

y = 12 , y′ =1.

Решение:

Если y′ = p ,

y′′ =

dpdx = 2

, то x dx

= 2x − p ,

−

–

однородное уравне-

ние первого порядка.

= u ,

p = ux ,

′

Тогда x

= u x +u , и уравнение

= 2

− x принимает вид:

′

u x +u = 2 −u .

′

2(1−u)

u x = 2(1

−u),

, ln c1 x

= −

ln(1−u) ,

2(1−u)

′

c1x = 1−u , c1x 1− x =1 , 1− x = c12 x2 , x =1− c12 x2 , p = x − c12 x = y

dy = xdx −

, откуда y =

−

ln x

+c .

c2 x

′

= x − c2 x .

Тогда y (x)

Из начальных условий:

+c2 ,

c2 = 0,

y(1)

= 0.

−

y′(1) =

1 =1

y =

Значит,

11.3.3. ДУ y′′ =

Уравнение y′ = p( y ), т.е.

тельно: y′′ = dpdx

f (y, y′)

явно не содержит независимую переменную x. Пусть

dydx = p( y ) = p (y (x)) является сложной функцией y , следова- = dpdy dydx = dpdy p . Уравнение принимает вид: p dpdy = f ( y, p ),

откуда p = p( y,c1 ).

Для нахождения y получили уравнение dydx = p (y,c1 ), p (dyy,c1 ) = dx и общий интеграл имеет вид Φ( x, y,c1 ,c2 ) = 0 .

Пример:

Решите ДУ y′′ = (yy′)2 .

C2 xn−2

296

Лекции 10 - 11

Решение:

Пусть y′ = p( y) , тогда y′′ =

и p

−

= 0 .

p = 0,

Это уравнение равносильно совокупности решений

Решением первого уравнения совокупности dy = 0 является y = c .

Найдем решение второго:

= ln

+ lnc

( c ≠ 0 ) ,

p = dy = c y ,

dy = c ydx ,

= c dx , lny = c x + lnc

( c

≠ 0 ) ,

y = c ec2 x .

Ответ: y

= c ,

= c ec2 x .

11.4.Таблица 2. Решение ДУ второго порядка, допускающих понижение порядка

		Вид ДУ				Метод решения
1.	y′′ =	f (x)	Последовательное интегрирование

2.	y′′ = f (x, y′)		p(x) = y′, p′ = y′′

3.	y′′ = f (y, y′)		p( y) = y′, y′′ = dp p
							dy
	y′′ =	y − xy′		y			y − xy′
4.			p =		, p′ =
		x2		x			x2
5.	yy′′+ y′2 = x		p = yy′, p′ = y′2 + yy′′

11.5. ДУ n-го порядка, допускающие понижение порядка

11.5.1. ДУ вида y(n) = f ( x) .

Общее решение получается путем n-кратного интегрирования. Принимая во внимание, что

y(n) = (y(n−1) )' , y(n−1) = ∫ f (x)dx + C1 ,

y(n−2) = ∫(∫ f (x)dx)dx +C1x +C2 , …,

C xn−1

y = ∫...∫ f (x)dx...dx + (n1−1)! + (n − 2)! +... + Cn .

Дифференциальные уравнения

297

Пример:

Найдите частное решение ДУ y′′′ = e2 x , удовлетворяющее начальным ус-

ловиям: y0 =1 , y0′ = −1 , y0′′ = 0 при x0 = 0 . Решение:

Последовательное интегрирование дает:

y′′ =

2 x

+c1 , y′ =

2 x

2 e

4 e

+c1x +c2 , y =

8 e

+c1

+c2 x +c3 .

Из начальных условий y(0) =1

′

= −1,

′′

, y (0)

y (0) = 0 , что приводит к сис-

теме для определения постоянных c1, c2 , c3 :

+c3 ,

1 =

= −

+ c2 , откуда

, и

y =

2 x

−

x +

−1

= −

0 = 1 + c ,

c = 7

Пример:

Найдите

общий

интеграл

уравнения

y " = sin(kx)

и частное

решение,

удовлетворяющее начальным условиям y |x=0 = 0,

y ' |x=0 =1 .

y ' = ∫sin kxdx +C1 = − 1 cos kx +C1 ,

y =

−

cos kx +C1

+ C2 =

∫

= −∫k cos kxdx + ∫C1dx +C2 = −

sin kx + C1x +C2

общее решение. Из

условия y |x=0 = 0 находим 0 = С2 .

Из условия y ' |

x=0

находим: 1 = − 1 +C → C =1 + 1 .

Таким образом, частное решение имеет вид:

y = −

sin kx

+ x 1

11.5.2. ДУ вида F (y, y ', y",..., y(n) )= 0

Уравнение не содержит в явном виде независимую переменную x . Порядок уравнения понижается на единицу подстановкой:

y ' = P(y), y" = dP				= dP dy	= dP
		dx		dy dx	dy
= P	d 2 P dy	+	dP dy dP		= P	2
	dy2 dx			dy dx dy

				d
P, y '" =				d	dP P		=
P, y '" =					dP P		=
				dx		dy
	2					2
d	2	P2	+ dP			P .
d		P2	+ dP			P .
dy			dy

298

Лекции 10 - 11

Пр

им

ер:

Найдите общий интеграл уравнения y '2 + 2 yy " = 0 .

Подстановка y ' = P (y)

, y" = dP P

в уравнение дает:

dP (y)

P (y)= dydx = 0,

y = const;

P (y)+ 2 y

P (y)

= 0

P + 2 y dP = 0;

2 y dP = −P, dP = − dy , ln

= − 1 ln

+ ln C ,

P = C y−12

2 y

dy =

;

ydy = C dx;

2 y 2 = C x +C

11.5.3. ДУ вида F (x, y(k ),..., y(n) )= 0

Уравнение не содержит в явном виде функцию

y и ее производные до

(k −1) порядка включительно. Порядок уравнения понижается на k единиц с помощью замены y(k ) = P (x). Имеем F (x, P, P ',..., P(n−k ) )= 0. Если для последнего уравнения найдено решение P (x) = ϕ (x,C1 ,C2 ,...,Cn−k ), то искомая функция y (x) получается путем k - кратного интегрирования функции

P (x) = ϕ (x,C1 ,C2 ,...,Cn−k ).

Пример:

Найдите общий интеграл уравнения xy '"+ y "− x −1 = 0 . В уравнении явно не содержатся функции y, y ' .

Сделаем замену y " = P (x) → y '" = dPdx . Подстановка приводит к линейному

уравнению: P '+ Px = 1x +1.

Решение ищем в виде:

P (x) = u (x)υ (x), P ' = u 'υ +υ ' u, u 'υ +υ ' u +

uυ

+1,

1 + x

+ u

'υ =

υ '+

υ '+υ

= 0,

dυ

= −

υ ;

dυ

= − dx ,

= −ln

→ υ = 1 , u 'υ =

1+ x

u ' 1

1+ x

Дифференциальные уравнения

299

u ' =1 + x, du = (1 + x)dx, u =

+ x +C , P = uυ, P =

+ x +C

∫

P =

1 , y " =

+1 +

1 ,

y ' =

+1 +

dx + C2 =

+ x +C ln

, y =

+ x +C

dx +C

∫

u = ln x

∫ln xdx =

= x ln x − ∫x

1 dx

du = x dx

= x ln x − x = x (ln x −1);

dυ = dx

υ = x

y =

+C1x (ln x −1)+C2 x +C3 .

11.5.4. ДУ вида dxd G (x, y, y ',..., y(n−1) (x))= 0

Левая часть ДУ такого вида может быть представлена в виде полной производной по x от некоторой функции. Покажем, что интегрирование по x понижает порядок уравнения на единицу.

Пример:

xy '"+ y "− x −1 = 0, (xy ")' =			x2		+ x	', xy " =	x2	+ x +C ,
xy '"+ y "− x −1 = 0, (xy ")' =					+ x	', xy " =		+ x +C ,
				2		2		1
				2		2
y " =	x	+1 + C1 .
y " =		+1 + C1 .
2		x

В результате изучения материала, изложенного в этих лекциях, студенты должны различать и уметь решать:

основные типы ДУ первого порядка,

некоторые типы ДУ второго порядка, приводимые к ДУ первого порядка,

ДУ n-го порядка, допускающие понижение порядка.

Лекции 12 - 13 ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

В лекции рассмотрены линейные дифференциальные уравнения (ЛДУ) и методы их решения. Особое внимание уделено линейным ДУ с постоянными коэффициентами, возникающим как простейшая математическая модель явления при рассмотрении многих задач естественных и прикладных наук.

12.1.Общая теория линейных дифференциальных уравнений высшего порядка. Определения и общие свойства

12.2.Решение ОЛДУ второго порядка с постоянными коэффициентами

12.3.Таблица 3. Решение ОЛДУ второго порядка

12.4.ОЛДУ n-го порядка с постоянными коэффициентами

12.5.Таблица 4. ОЛДУ n-го порядка

12.6.НЛДУ второго порядка

13.1.Решение НЛДУ второго порядка методом вариации произвольных постоянных

13.2.Решение НЛДУ второго порядка с постоянными коэффициентами методом неопределенных коэффициентов

13.3.Таблица 5. Решение НЛДУ y′′+ py′+ qy = f (x)

13.3.1.Метод неопределенных коэффициентов

13.3.2.Метод вариации произвольной постоянной

13.3.3.Принцип суперпозиции

13.4.НЛДУ высших порядков

13.4.1.Метод вариации произвольных постоянных

13.4.2.Метод неопределенных коэффициентов

13.5.Таблица 6. Решение НЛДУ n-го порядка

13.5.1.Метод неопределенных коэффициентов

13.5.2.Метод вариации произвольной постоянной

12.1.Общая теория линейных дифференциальных уравнений высшего порядка. Определения и общие свойства

ОЛинейным называется ДУ, содержащее функцию у и ее производные в первой степени.

ОНеоднородным линейным дифференциальным уравнением (НЛДУ) n-го порядка называется ДУ вида:

y(n) + a1 y(n−1) +... + an y = f (x) ,

Линейные дифференциальные уравнения

301

где ai (i =1,2,...,n) и f (x) - непрерывные функции от х или постоянные, причем правая часть f (x) ≠ 0 .

ОЛинейное ДУ называется однородным (ОЛДУ), если f (x) = 0 . Рассмотрим ОЛДУ второго порядка:

y′′+ a1 y′+ a2 y = 0 .

Пусть y1 = y1(x) и y2 = y2 (x) - частные решения ДУ.

ОДва решения ДУ y1 и y2 называются линейно независимыми, если их линейная комбинация c1 y1 + c2 y2 = 0 лишь в случае c1 = c2 = 0 .

Решения y1 и y2 будут линейно зависимы тогда и только тогда, когда

y2 = cy1 .

Например,

функции

= ex

и y

= 3ex

- линейно зависимы, а функции

y = ex

и y

= e−x - линейно независимы.

Если

являются

функциями

x ,

то

определитель

W (y1, y2 )=

= y1 y2′ − y1′y2 называется определителем Вронского.

y1′

y2′

Если функции

линейно зависимы на [a,b] ,

то

W (y1, y2 )≡ 0 ,

x [a,b] .

Доказательство:

λy1

y2 = λy1 → y2′ = λy1′ и W (y1, y2 )

= λ

= 0 .

y1′ y2′

y1′

λy1′

y1′

Если

решения

ДУ

линейно

независимы

на

[a,b] , то

W (y1, y2 )≠ 0, x [a,b] .

Доказательство:

Допустим противное: W (y1, y2 )= 0 ,

тогда

y1 y2′ − y1′y2 = 0 . Для y1 ≠ 0 :

y y′

− y′y

′

1 2

= 0 ,

т.е.

= 0 и

= const ,

что противоречит условию,

значит, W ≠ 0 .

ТЕсли y1 и y2 - линейно независимые частные решения ОЛДУ второго

порядка y′′+ a1 y′+ a2 y = 0 , то общее решение ДУ равно линейной ком-

302	Лекции 12 - 13

бинации этих частных решений y = c1 y1 + c2 y2 , где c1,c2 - произвольные по-

стоянные.

Доказательство:

y1′′+ a1 y1′ + a2 y1 = 0, y2′′ + a1 y2′ + a2 y2 = 0.

Подставим решение в виде y = c1 y1 + c2 y2 в исходное уравнение:

(c1 y1 + c2 y2 )″ + a1 (c1 y1 + c2 y2 )′ + a2 (c1 y1 + c2 y2 )=

=c1 (y1′′+ a1 y1′ + a2 y1 )+ c2 (y2′′ + a1 y2′ + a2 y2 ) = c1 0 + c2 0 = 0 ,

значит, y = c1 y1 + c2 y2 - общее решение ОЛДУ при любом выборе постоянных.

Пример:

Решите уравнение (x −1)y′′− xy′+ y = 0 .

Решение:									= ex
Подстановкой	в уравнение убеждаемся, что				функции	y = x,	y	2	= ex
			y2			1		2
удовлетворяют уравнению, причем			y2	≠ const	, т.е. они линейно незави-
удовлетворяют уравнению, причем			y	≠ const	, т.е. они линейно незави-
			y
			1
симы, значит	y = c x +c ex .
	1	2

ТЕсли известно одно частное решение ОЛДУ 2-го порядка y1 , то второе

частное решение, линейно независимое с первым, находится интегрированием линейного дифференциального уравнения (ЛДУ) первого порядка.

Доказательство:

Пусть y′′+ a1 y′+ a2 y = 0 ; y1 - частное решение, значит, y1′′+ a1 y1′ + a2 y1 = 0 . Второе частное решение ищем в виде y2 = u(x) y1 , где u(x) - неизвестная функция.

Подставим y2 в ДУ: (y1′′+ a1 y1′ + a2 y1 ) u + y1u′′+ (2 y1′ + a1 y1 )u′ = 0 , y1u′′+ (2 y1′ + a1 y1 )u′ = 0 . Заменой u′ = p , приходим к ДУ первого порядка

для нахождения функции р:			y1 p′+ (2 y1′ + a1 y1 ) p = 0 , интегрирование ко-
торого		позволяет найти	функцию u(x) и y2 = u(x) y1 , т.е.
y2 = y1 ∫	e−∫a1dx	dx .
y2 = y1 ∫	y2	dx .
	1

12.2.Решение ОЛДУ второго порядка с постоянными коэффициентами

Рассмотрим уравнение

Линейные дифференциальные уравнения			303
	y′′+ py′+ qy = 0 .		(*)
Ищем его решение в виде y = ekx		(подстановка Эйлера), найдем значения k .
Продифференцируем y : y′ = kekx ,		y′′ = k2ekx . Подстановка такого вида реше-
ния в ДУ дает: k2ekx + pkekx + qekx = 0 , k2 + pk + q = 0 .
	Уравнение
О
	k2 + pk + q = 0		(**)

называется характеристическим уравнением ОЛДУ для определения k .

Решения характеристического уравнения имеют вид:

		k	= −	p	±	p2	− q .
		k	= −		±		− q .
		1,2		2		4
				2		4
Возможны следующие виды решений:
1). Если D =	p2	− q > 0 , то характеристическое уравнение имеет два действи-
1). Если D =	4
	4
тельных различных корня k1 и k2 ,			k1 ≠ k2 .

В этом случае ОЛДУ имеет два линейно независимых ( k1 ≠ k2 ) различных ча-

стных решения y = ek1x ,

= ek2 x

. Общее решение ДУ имеет вид:

k x

, где k

− q .

y = c e 1

+ c e 2

= −

1,2

Пример:

Найдите решение ОЛДУ y′′− 2 y′−8y = 0 .

k 2 − 2k −8 = 0, k1 = 4, k2 = −2, y = c1e4 x + c2e−2x .

2). Если D =

− q = 0 ,

то k

= k

и характеристическое уравнение имеет ко-

рень k = −

кратности два. Одно частное решение имеет вид:

y = e−

. Вто-

рое линейно независимое частное решение ищем в виде:

= y u(x) = e−

u ,

тогда

−

y2′ = e

u′

+ e

−

= e

2 u′−

304

Лекции 12 - 13

−

y2′′ = e

2 u′′

−

u′

−

u′−

u = e

2 u′′− pu′+

u .

После подстановки

ОЛДУ

сокращения

на e−

получим

u′′− pu′+

u + pu′−

u + qu = 0 , и уравнение для u(x)

принимает вид:

u′′+ q −

u = 0 .

В рассматриваемом случае равных корней характеристического уравнения

− p x

ложим, C1 =1, C2 = 0 , тогда y2 = xe 2 .

Общее решение ОЛДУ в случае k1 = k2 = k имеет вид:

y= ekx (c1 + c2 x), где k = − 2p .

!Убедиться в том, что выражение y2 = xekx является вторым линейно независимым решением дифференциального уравнения при условии, что

k = − 2p является решением характеристического уравнения, можно не-

посредственной подстановкой.

Пример:

y′′−6 y′+ 9 y = 0 .

k 2 − 6k + 9 = 0, k1 = k2 = 3 ± 9 − 9 = 3, y = (c1 + c2 x)e3x .

3). Если D =

− q < 0 , то характеристическое уравнение имеет два сопря-

женных комплексных корня

k = −

± i q −

, k =α + βi,

=α − βi , где

1,2

α = −

, β =

q −

Частные решения имеют вид:

y = e(α+βi) x ,

= e(α−βi) x .

Общее решение y =

e(α+βi) x

e(α−βi) x = eαx (

eiβx +

e−iβx ), где

- та-

кие комплексные постоянные, что у – действительная функция.

Линейные дифференциальные уравнения

305

По формуле Эйлера: eiβx = cos β x +i sin β x , e−iβx = cos β x −i sin β x , тогда y = eαx (c1 + c2 )cos βx +i (c1 −c2 )sin βx . Полагая c1 + c2 = c1 , i(c1 −c2 )= c2 , c1,c2 - действительные постоянные, получим общее решение ОЛДУ в виде

y = eαx (c cos β x + c

sin β x), где k

= −

± i q −

=α ± i

β .

1,2

4). В частном случае

y′′+ β2 y = 0 , когда

p = 0,

q = β2 , α = 0 , k1,2

= ±βi , об-

щее решение имеет вид: y = c1 cos βx + c2 sin βx .

Пример:

y′′− 6 y′+13y = 0 .

y = e3x (c1 cos 2x + c2 sin 2x).

k 2 − 6k +13 = 0, k = 3 ± 2i, α = 3, β = 2 ,

12.3. Таблица 3. Решение ОЛДУ второго порядка y′′+ py′+ qy = 0, k 2 + pk + q = 0

Корни характеристического уравнения

Вид общего решения

1. D > 0, k = −

− q =

y = c1e

k x

+ c2e

k x

1,2

действительные, разные.

2. k = k = k = −

y = (c1 + c2 x)e

действительные, равные, кратность 2.

3. k =α ±iβ, α = −

β =

q −

y = e

αx

(c1 cos

β x + c2 sin β x)

1,2

комплексные.

4. k1,2

= ±iβ, α = 0

y = c1 cos β x + c2 sin β x

306	Лекции 12 - 13
12.4. ОЛДУ n-го порядка с постоянными коэффициентами
y( n) + a1 y( n-1) + ...+ an y = 0,	ai = const

ОФункции ϕ1(x), ϕ2 (x),...,ϕn (x) называются линейно независимыми, ес-

ли никакая	из них линейно не	выражается через другие для всех
x [a,b] , т.е.	c1ϕ1 + c2ϕ2 +... + cnϕn	≠ 0 , если ci - постоянные, не все рав-
ные нулю.

ТЕсли функции y1, y2 ,..., yn являются линейно независимыми частными

решениями ОЛДУ n-го	порядка, то его общее решение есть
y = c1 y1 + c2 y2 +... + cn yn , где	ci - произвольные постоянные. Число ли-

нейно независимых частных решений ДУ равно степени характеристического уравнения или порядку ОЛДУ. Найдя n частных решений, можно записать общее решение ОЛДУ.

Составим характеристическое уравнение ОЛДУ n-го порядка с постоянными коэффициентами: kn + a1k n−1 + a2kn−2 +... + an = 0 . Найдем его корни

k1,k2 ,...,kn .

В зависимости от корней характеристического уравнения частные линейно независимые решения ОЛДУ имеют разный вид.

1). Каждому действительному однократному корню k соответствует частное решение вида y = ekx .

2). Каждому действительному корню k кратности r соответствует r линейно независимых решений:

y1 = ekx ,

y2 = xekx ,

y3 = x2ekx ,

...................

yr = xr−1ekx

3). Каждой паре комплексных корней k1,2 =α ±iβ соответствуют два частных решения:

y1 = eαx cos β x,y2 = eαx sin β x.

Линейные дифференциальные уравнения

307

4). Каждой паре комплексных корней k1,2 =α ±iβ кратности µ соответствует 2µ частных решений:

y1 = eαx cos β x,

y2 = xeαx cos β x,

..........

yµ = xµ−1eαx cos β x,

yµ+1 = eαx sin β x,

yµ+2 = xeαx sin β x,

..........

y2µ = xµ−1eαx sin β x.

12.5. Таблица 4. ОЛДУ n-го порядка

y( n) + a1 y( n-1) + a2 y( n-2 ) + ...+ an y = 0, ai = const , k n + a1k n-1 + a2 k n-2 + ...+ an = 0

Корни характеристического уравнения		Вклад указанных корней в общее
			решение ДУ
1.	Действительные, разные	y = c ek1x	+ c ek2 x		+... + c ekn x
	k1 ≠ k2 ≠ k3 ≠... ≠ kn	1	2		n
		1	2		n

2.	Действительные, кратности r ≤ n	y = (c1 + c2 x + c3 x2 +... + cr xr−1 )ekx
	k1 = k2 = k3 =... = kr = k
3.	Комплексные, разные	y = eα1x (c1 cos β1x + c2 sin β1x)+
	k1 =α1 ±iβ1, k2 =α2 ±iβ2 ,...	+eα2 x (c3 cos β2 x + c4 sin β2 x)+... +
	..., kn =αn ±iβn , α1 ≠α2 ≠ ... ≠αn ,	+eα2 x (c3 cos β2 x + c4 sin β2 x)+... +
	..., kn =αn ±iβn , α1 ≠α2 ≠ ... ≠αn ,	+eαn x (c2n−1 cos βn x + c2n sin βn x).
	β1 ≠ β2 ≠ ... ≠ βn .	+eαn x (c2n−1 cos βn x + c2n sin βn x).

4.	Комплексные, кратности r = 3	y = eαx [	(c1 + c2 x + c3 x2 )cos β x +
	k1 = k2 = k3 =α + iβ	+(c4 + c5 x + c6 x		2	) sin β x ]
		+(c4 + c5 x + c6 x			) sin β x ]

308																						Лекции 12 - 13
	Пример:
	Пример:
		Решите уравнение y′′′− y = 0 .
		Решение:													(k −1)			(			)
		Характеристическое уравнение: k3 −1 = 0,																(			)				,
		Характеристическое уравнение: k3 −1 = 0,																	k 2 + k +1 = 0						,
		откуда k	=1 , k		= − 1 ±i	3	.
		откуда k	=1 , k	2,3	= − 1 ±i		.
		1		2,3	2	2
					2	2
		Частные решения имеют вид:						y = ex ,				y		= e−		x	cos		3	x , y	= e−			x	sin	3	x .
													2			2			3					2		3
																2								2
								1											2	3						2
																			2							2
									x		−	x					3				3
									x		−						3				3
		Общее решение имеет вид: y = c1e								+ e 2			c2		cos				x + c3 sin				x .
		Общее решение имеет вид: y = c1e								+ e 2			c2		cos		2		x + c3 sin		2		x .
																	2				2
12.6. НЛДУ второго порядка
	НЛДУ второго порядка имеет вид:							y′′+ a1 y′+ a2 y = f (x) , где ai																	и	f (x) -
известные функции.

ТОбщее решение НЛДУ yO.H . = y равно сумме общего решения yO.O. = y

соответствующего однородного уравнения y′′+ a1 y′+ a2 y = 0 и частного

решения	yЧ.Н. = y	данного	неоднородного	уравнения
y′′+ a1 y′+ a2 y = f (x) , то есть y = y + y .
Доказательство:		y′′+ a1 y′+ a2 y = 0,	y′′+ a1 y′+ a2 y = f (x) . Сложим
Для y , y	справедливо:

эти уравнения почленно: (y + y)″ + a1 (y + y)′ + a2 (y + y)= f (x) , значит, y = y + y является общим решением НЛДУ.

13.1.Решение НЛДУ второго порядка методом вариации произвольных постоянных

Пусть известно общее решение ОЛДУ y = c1 y1 + c2 y2 , где c1,c2 − const .

Найдем общее решение НЛДУ методом вариации произвольных постоянных. Будем искать общее решение НЛДУ в виде y(x) = c1 (x) y1 + c2 (x) y2 , считая c1

и c2	неизвестными функциями x . Найдем c1(x), c2 (x) .	Вычислим производ-
ную:	y′ = c1 y1′ + c1′y1 + c2 y2′ + c2′y2 . Подберем c1(x) и	c2 (x) так, чтобы

c1′y1 + c2′y2 = 0 , тогда y′ = c1 y1′ + c2 y2′ , а y′′ = c1 y1′′+ c1′y1′ + c2 y2′′ + c2′y2′ .

Линейные дифференциальные уравнения

309

Подстановка этих выражений в НЛДУ дает:

(c1 y1′′+ c1′y1′ + c2 y2′′ + c2′y2′ )+ a1 (c1 y1′ + c2 y2′ )+ a2 (c1 y1 + c2 y2 ) = f (x) ,

c1 (y1′′+ a1 y1′ + a2 y1 )+ c2 (y2′′ + a1 y2′ + a2 y2 )+ c1′y1′ + c2′y2′ = f (x) .

Выражения в круглых скобках равны нулю, так как y1

и y2

- частные реше-

ния

соответствующих ОЛДУ.

Значит,

c1′y1′ + c2′y2′ =

f (x) .

Получаем, что

yO.H . = c1(x) y1 + c2 (x) y2 , если c1(x) и c2 (x)

удовлетворяют системе:

c′y

+ c′y

= 0,

′

= f (x).

c1 y1

+ c2 y2

Для

линейно

независимых

функций

определитель системы

∆ =W (y1, y2 ) ≠ 0 ,

и можно найти решение системы: c1′ =ϕ1(x),

c2′ =ϕ2 (x) и

искомые функции c1(x) = ∫ϕ1(x)dx + c1,

c2 (x) = ∫ϕ2 (x)dx + c2 .

Пример:

Найдите решение НЛДУ:

y′′−

y′

= x .

Найдем решение ОЛДУ: y′′−

y′

= 0 ,

y′′

ln y′ = ln x

+ln c ,

y′

y′ = cx , yO.O. = c1x2 +c2 .

Частные решения ОЛДУ:

= x2 ,

=1.

Найдем yO.H . = c1 (x) y1 + c2 (x) y2 .

c′y

+c′y

c′ x2

+c′

1 = 0,

1 1

c1′y1′ +c2′y2′ = f (x),

2c1′ x +c2′ 0 = x.

Отсюда c1′ = 1 , c2′

= −

1 x2

c1 =

+c1,

= −

+c2 .

x2 +

−

1 =

−

+ c x2 + c =

+c x2

+c .

O.H .

13.2.Решение НЛДУ второго порядка с постоянными

коэффициентами методом неопределенных коэффициентов y′′+ py′+ qy = f ( x)

Ранее (п. 12.6) доказано,	что общее решение НЛДУ имеет вид:
yO.H . = yO.O. + yЧ.Н. = y + y , где y	- общее решение соответствующего ОЛДУ,

310	Лекции 12 - 13

характеристическое уравнение которого k2 + pk + q = 0 , а y - частное реше-

ние НЛДУ.

Частное решение НЛДУ y может быть найдено методом неопределенных коэффициентов для некоторых видов функции f (x) в правой части

уравнения и корней характеристического уравнения его левой части. Рассмотрим следующие случаи:

1. Если f (x) = aeαx , a ≠ 0 , то y нужно искать в виде y = Aeαx , где А – произвольная постоянная, подлежащая определению. Последовательное

дифференцирование дает: y′ = Aαeαx , y′′ = Aα2eαx .			Подставляя эти выраже-
ния в НЛДУ и сокращая на eαx , получим
		A(α2 + pα + q)= a .				(*)
1).		Если α не является корнем характеристического		уравнения, т.е.
	2	+ pα + q ≠ 0 , то уравнение (*) имеет решение A =	a		αx
α					и y = Ae	.
			α2 + pα + q

2). Если α является корнем характеристического уравнения, то y нужно искать в другом виде. Так, если α - простой (однократный) корень характеристического уравнения, то y = Axeαx ; если α - двукратный корень характеристического уравнения, то y = Ax2eαx .

Пример:

Найдите решение НЛДУ y′′− 5y′+ 6 y = ex .

Решение:

Для ОЛДУ y′′−5y′+ 6 y = 0 ,

k 2 −5k + 6 = 0 ,

k1 = 3, k2

= 2 и y = c1e3x + c2 e2x . Для

f (x) = e

α =1,

так как k1, k2 ≠ α , то

. Найдем А. y ′ = Ae

y ′′ = Ae

Подстановка в уравнение дает: Aex

−5Aex + 6Aex

= ex , откуда 2 A = 1, A = 1

y =

2 e

y = y + y = c1e

+ c2 e

Окончательно,

2 x

2.f (x) = ax2 + bx + c = P2 (x) .

Частное решение ищем в виде y = Q2 (x) = Ax2 + Bx + C ; найдем A, B, C. y′ = 2Ax + B, y′′ = 2A, 2A + 2Apx + pB + Aqx2 + Bqx + Cq = ax2 + bx + c ,

Aqx2 + (2Ap + Bq)x + (2A + Bp + Cq) = ax2 + bx + c .

Линейные дифференциальные уравнения	311
Неопределенные коэффициенты находятся из системы:
Aq = a,

2Ap + Bq = b,
	= c.
2A + Bp +Cq	= c.

1). Если число «0» не является корнем характеристического уравнения, то y = Ax2 + Bx + C ;

2). Если число «0» является простым корнем характеристического уравнения, тогда частное решение нужно искать в виде y = x(Ax2 + Bx + C ).

3). Если число «0» является двукратным корнем характеристического уравнения, тогда y = x2 ( Ax2 + Bx + C) .

Пример:
Решите ДУ	y	′′	= x	2	+ y , если	y(0)	= −2,	′	=1.
Решите ДУ	y		= x		+ y , если	y(0)	= −2,	y (0)	=1.
Решение
Для ОЛДУ y′′− y = 0, k2 −1 = 0,							k1 =1,	k2 = −1 и y = c1ex +c2e−x .

Так как f (x) = x2 , y = Ax2 + Bx +C .

Значит, 2A −( Ax2 + Bx +C) = x2 .
−A =1,
		откуда A = −1, B = 0,C = −2 и y = −x			2	−2 .
−B = 0,		откуда A = −1, B = 0,C = −2 и y = −x				−2 .

2A −C = 0,
y = y + y = c1ex + c2e−x −(x2 + 2) , y′ = c1ex −c2e−x −2x .
При x = 0			′	=1,
При x = 0	y(0) = −2, y (0)			=1,
−2 = c1 +c2 − 2;

1 = c1 −c2 ,
откуда c	= 1	, c = − 1 .
1	2	2	2
	2		2

Общее решение НЛДУ имеет вид: y = 12 (ex −e−x )−(x2 + 2).

3. Если f (x) = Pn (x) , α = 0 , то решение y нужно искать в следующем виде:

1)если число «0» не является корнем характеристического уравнения, то y = Qn (x) ;

2)если число «0» является простым корнем характеристического уравнения, то y = xQn (x) ;

3)если число «0» является двукратным корнем характеристического уравнения, то y = x2Qn (x) , где Qn (x) - многочлен n-го порядка с коэффициентами, подлежащими определению.

312	Лекции 12 - 13

4.Если f (x) = Pn (x)eα x , где Pn (x) - многочлен n-го порядка, то решение y

нужно искать в следующем виде в зависимости от значений корней характеристического уравнения:

1) если α не	является корнем характеристического уравнения, то
y = Q (x)eα x ,	где Q - многочлен n-ой степени с неопределенными ко-
n	n

эффициентами, подлежащими определению подстановкой в НЛДУ;

2)если α - простой (однократный) корень характеристического уравнения,

то y = xQn (x)eα x ;

3) если α - двукратный корень характеристического уравнения, то

y= x2Qn (x)eα x .

5.f (x) = M cos βx + N sin βx .

Будем искать частное решение в виде

y = Acos βx + Bsin βx ,

найдем А и В.

y′ = −Aβ sin βx + Bβ cos βx ,

y′′ = −Aβ2 cos βx − Bβ2 sin βx . Подстановка

НЛДУ дает:

(−Aβ2 + Bpβ + Aq)cos βx + (−Bβ2 − Apβ + Bq)sin β x = M cos β x + N sin β x .

Из системы

A(q − β2 )+ Bpβ = M ;

−Apβ + B(q − β2 )= N

найдем А и В.

1).

Если число iβ не является корнем характеристического уравнения,

то

y = Acos βx + Bsin βx ;

2).

Если число iβ

является

корнем

характеристического

уравнения,

то

y = x(Acos βx + Bsin βx).

Пример:

Решите уравнение y′′−4 y′+ 4 y = cos x .

Решение:

4 − 4 = 2 , y = (c1 +c2 x)e2 x .

y′′−4 y′+ 4 y = 0 , k2 −4k + 4 = 0 , k1,2 = 2 ±

β =1, k1,2

≠ β : y = Acos x + B sin x .

Найдем А и В.

y′ = −Asin x + B cos x, y′′ = −Acos x − B sin x ;

(−Acos x − B sin x)−4(−Asin x + B cos x)+ 4(Acos x + B sin x)= cos x ;

(−A −4B + 4A)cos x +(−B + 4A + 4B)sin x = cos x ;

3A −4B =1,

4A +3B = 0, → A

, B

= −

y =

cos x −

sin x

;

y = (c1 +c2 x)e2 x +

cos x −

sin x .

Линейные дифференциальные уравнения

313

Пример:

Найдите решение НЛДУ y′′+ 4 y = cos 2x .

Решение:

+ 4 = 0 → k1,2 = ±2i

. y = y

+ y .

y = c1 cos 2x +c2 sin 2x . Так как 2i является корнем характеристического

уравнения:

y = x (Acos 2x + B sin 2x),

y′ = 2x (−Asin 2x + B cos 2x)+ Acos 2x + B sin 2x ,

y′′ = 4x (−Acos 2x − B sin 2x)+ 4(−Asin 2x + B cos 2x).

Подстановка в уравнение дает:

(−4Ax + 4B + 4Ax)cos 2x +(−4Bx − 4A + 4Bx)sin 2x = cos 2x ,

откуда

4B =1,

−4A = 0,

→ A = 0,

B = 4 ,

sin 2x

y = c cos 2x +c

sin 2x +

sin 2x .

Если f (x) = P (x)eαx cos βx + Q (x)eαx sin βx , то

y в зависимости от кор-

ней характеристического уравнения нужно искать в виде:

если число α +iβ не является корнем характеристического уравнения,

то y = Rp (x)eαx cos βx +Vp (x)eαx sin βx , где Rp (x)

и Vp (x) - многочлены с

неопределенными коэффициентами, степень которых равна наивысшей

степени многочленов Pn (x)

и Qm (x) , p = max(n,m) ;

2)если число α +iβ является корнем характеристического уравнения, то

y= x[Rp (x)eαx cos β x +Vp (x)eαx sin βx].

!Указанный вид частного решения сохраняется и в тех случаях, когда

один из многочленов равен нулю, т.е. f (x) = Pn (x)eαx cos βx или

f(x) = Qm (x)eαx sin βx .

ТПусть НЛДУ таково, что его правая часть представляет собой сумму не-

скольких, например, двух функций y′′+ a1 y′+ a2 y = f1(x) + f2 (x) . Тогда если y1 - частное решение y′′+ a1 y′+ a2 y = f1(x) , а y2 - частное решение

y′′+ a1 y′+ a2 y = f2 (x) , то	частное решение исходного НЛДУ есть
суперпозиция этих двух:	y = y1 + y2 .

314 Лекции 12 - 13

13.3. Таблица 5. Решение НЛДУ y′′+ py′+ qy = f ( x) y = yO.O. + yЧ.Н. = y + y

13.3.1. Метод неопределенных коэффициентов

f (x)	Корни		Вид yЧ.Н.	= y
f (x)	характеристического		Вид yЧ.Н.	= y
	уравнения

1. Pn (x)	а) 0 – не корень	y = Qn (x)
1. Pn (x)	б) 0 – корень кратно-	y = xrQ (x)
	сти r (r =1,2)		n
	а) α – не корень	αx	Qn (x)
2. eαx P (x)	б) α – корень крат-	y = e	Qn (x)
n	ности r (r =1,2)	y = xreαxQn (x)

3. Acos βx + Bsin βx	а) iβ – не корень	y = A1 cos βx + Bsin βx
3. Acos βx + Bsin βx	б) iβ – корень	y = xr (A1 cos βx + B1 sin β x)

4. P (x)cos βx +	а) iβ – не корень	y = Qk cos βx + Mk sin βx ,
4. P (x)cos βx +	а) iβ – не корень	y = xr [Q cos βx + M sin βx],
n	б) iβ – корень	y = xr [Q cos βx + M sin βx],
+Rm (x)sin βx	б) iβ – корень		k	k
			k	k
		k = max(n,m) .

5. eαx[P (x)cos βx +	а) α +iβ – не корень	y = eαx[Q cos βx + M			k	sin βx],
n	б) α +iβ – корень		k		k
+Rm (x)sin βx]	б) α +iβ – корень	y = xreαx[Qk cos βx + Mk sin βx]
+Rm (x)sin βx]	кратности r (r =1,2)	y = xreαx[Qk cos βx + Mk sin βx]
	кратности r (r =1,2)

Здесь Q и M – многочлены с неизвестными коэффициентами.

13.3.2. Метод вариаций произвольной постоянной

yO.H . = c1(x) y1 + c2 (x) y2 , если y1 и y2 - частные решения ОЛДУ и

c1′y1 + c2′y2 = 0,c1′y1′ + c2′y2′ = f (x).

13.3.3. Принцип суперпозиции

Если f (x) = f1(x) + f2 (x) +... + fn (x) , то y = y1 + y2 +... + yn .

Линейные дифференциальные уравнения

315

13.4. НЛДУ высших порядков

y(n) + a y(n−1)	+... + a	n	y = f (x), a (i =1,2,...,n) , f (x) – непрерывные функ-
1		n	i

ции или постоянные. Пусть известно общее решение y = c1 y1 + c2 y2 +... + cn yn соответствующего ОЛДУ: y(n) + a1 y(n−1) +... + an y = 0 .

13.4.1. Метод вариации произвольных постоянных

Общее решение НЛДУ имеет вид

y = c1(x) y1 + c2 (x) y2 +... + cn (x) yn ,

где

yi (i =1,2,…, n) – частные решения ОЛДУ, а ci = ci (x) (i =1,2,…, n) –

функции, производные которых удовлетворяют системе уравнений:

+ c2′y2

+... + cn′ yn = 0,

c1′y1

c1′y1′ + c2′y2′ +... + cn′ yn′ = 0,

..............................................

(*)

′

(n−2)

′

(n−2)

′

(n−2)

= 0,

c1 y1

+ c2 y2

... + cn yn

′

(n−1)

′

(n−1)

′

(n−1)

c1 y1

+ c2 y2

+... + cn yn

= f (x),

т.е. являются решением

этой

системы

{c1′(x),c2′(x),...,cn′(x)}

при

∆ =W (y1, y2 ,..., yn )≠ 0

для

линейно

независимых частных решений

y1, y2 ,..., yn и имеют вид:

(x) = ∫c1′dx + c1,

(x) = ∫c2′dx + c2 ,

...............................

∫

′

c (x) =

c dx + c .

Доказательство:

Продифференцируем у n раз, учитывая (*):

y = c1 y1 + c2 y2 +... + cn yn ,

y′ = c1 y1′ + c2 y2′ +... + cn yn′ ,

(остальные члены равны нулю из первого уравнения системы для ci′ (*)).

y(n−1) = c y (n−1)		+ c y	(n−1) +... + c y (n−1)	,
1 1		2 2	n n
y(n) = c y (n)	+ c y (n) +... + c y (n) + f (x) .
1 1	2	2	n n

316 Лекции 12 - 13

Умножим полученные выражения для производных на коэффициенты ai (i =1,2,...,n) и сложим их почленно. Суммы по вертикальным столбцам равны нулю, так как y1, y2 ,..., yn - частные решения ОЛДУ, ненулевыми

остаются слагаемые y(n) + a y(n−1)	+... + a		n	y = f (x) , значит y - решение
1			n
НЛДУ.
Пример:
	1
Найдите решение НЛДУ y′′′+ y′ =					.
Найдите решение НЛДУ y′′′+ y′ =		sin x			.
Решение:
1. Найдем частные решения ОЛДУ:
y′′′+ y′ = 0 ,	k3 + k = 0 , k1 = 0 , k2,3 = ±i .
Значит, y1 =1 , y2 = cos x, y3 = sin x .

2.Установим вид yO.O. = y : y = c1 +c2 cos x +c3 sin x .

3.Запишем вид yO.H . : y = c1 (x) +c2 (x) cos x +c3 (x)sin x .

4.Составим систему уравнений для определения ci′(x) :

+c′ cos x +c′ sin x = 0,

c′ 1

−c2′ sin x +c3′ cos x = 0,

−c2′ cos x −c3′ sin x =

sin x

Решением этой системы являются: c1′ =

c2′ = − cos x

c3′ = −1.

sin x

5. Найдем c (x) : c (x) =

= ln

∫sin x

c (x) =

∫

− cos x dx = −ln

sin x

+c ,

c (x) = −x +c .

sin x

6. Запишем решение:

+c1 +(−ln | sin x | +c2 )cos x +(−x + c3 )sin x =

y = ln

−cos x ln | sin x | −x sin x +c +c cos x +c

sin x.

= ln

13. 4.2. Метод неопределенных коэффициентов

уравнения и корней характеристического уравнения его левой части. Рассмотрим следующие случаи:

I.f (x)= P(x)eαx

1). Если α не является корнем характеристического уравнения, то частное решение ищем в виде y = R(x)eαx , гдеR(x) - многочлен с неизвестными коэффициентами, степень которого совпадает со степенью P(x);

Линейные дифференциальные уравнения

317

2). Если α корень кратности µ характеристического уравнения, то частное решение ищем в виде y = xµ R(x)eαx .

Пример:

yIV − y = x3 +1.

Характеристическое уравнение k4 −1 = 0, k4 =1, k	=1, k	2	= −1, k	3	= i, k	4	= −i .
1		2		3		4

Общее решение однородного уравнения:

y = C1ex +C2e−x + C3 cos x + C4 sin x .

Правая часть уравнения f (x) = x3 +1 имеет вид:

Pn (x)eαx , где n = 3, α = 0 ,

корни характеристического уравнения не совпадают с α . Частное решение ищем в виде:

y = Rn (x)eαx = R3 (x)e0 x = (A0 x3 + A1x2 + A2 x + A3 ), y ' = 3A0 x2 + 2 A1x + A2 ,

y " = 6A x + 2 A , y '" = 6A , y			IV	= 0, − A x3 − A x2		− A x − A = x3		+1.
0	1	0		0	1	2	3
Приравнивая коэффициенты при одинаковых					степенях x , получим:
−A =1, A = −1, A = 0, A = 0,					A = −1, y = −x3		−1.
0	0	1		2	3

Общее решение: y = C1ex + C2e−x + C3 cos x + C4 sin x − x3 −1.

II.f (x)= P(x)eαx cos βx + R(x)eαx sin βx

1). Если α +iβ не является корнем характеристического уравнения, то частное решение ищем в виде y = u (x)eαx cos βx +υ(x)eαx sin βx , где u (x), υ(x)- многочлены, степень которых равна наивысшей степени P(x) и

R(x).

2). Если α +iβ является корнем характеристического уравнения кратности µ , то частное решение: y = xµ u (x)eαx cos βx +υ(x)eαx sin βx .

Пример:

− y = 6sin x .

Характеристическое уравнение: k4 −1 = 0 , k =1,

= −1, k

= i, k

= −i .

Общее решение однородного уравнения

= C ex +C

e−x + C cos x + C

sin x ,

(x) = 6sin x

имеет вид:

318						Лекции 12 - 13

		f (x) = P (x)eαx cos β x + R (x)eαx sin β x, P (x) = 0, e0 x =1, α = 0, β =1 ,
	R0 (x) = 6, α +iβ = 0 + i 1 = i				совпадает с корнем k3 → решение ищем в
	виде:
	y = x (A0 cos x + B0 sin x), y ' = A0 cos x − A0 x sin x + B0 sin x + xB0 cos x ,
	y " = −2 A0 sin x + 2B0 cos x − A0 x cos x − B0 x sin x ,
	y '" = −3A0 cos x + A0 x sin x − 3B0 sin x − B0 x cos x ,
	y		= 4 A sin x + A x cos x − 4B cos x + B x sin x .
		IV
0				0	0	0

Подстановка этих значений в исходное уравнение дает

4 A0 sin x − 4B0 cos x = 6sin x, ,

откуда 4A0 = 6, A0 = 64 = 23 , B0 = 0 и

y= x 23 cos x, y = C1ex +C2e−x + C3 cos x +C4 sin x + 23 x cos x

13.5.Таблица 6. Решение НЛДУ n-го порядка

y( n) + a

y( n-1) + a

y( n-2 ) + ...+ a

y = f ( x),

= y

+ y

O.H.

O.O.

Ч.Н.

13.5.1. Метод неопределенных коэффициентов

Корни

Вид частного

Вид правой части

характеристического

решения

уравнения

f (x) = Pn (x)

а) число 0 не является

y = Qn (x)

корнем

многочлен степени n

б) число 0 является

y = xrQn (x)

корнем кратности r

а) число α не является

y = eαxQn (x)

αx

корнем

f (x) = e

(x)

б) число α является

y = xreαxQn (x)

корнем кратности r

Линейные дифференциальные уравнения				319

		а) число iβ не является	y = A cos βx + B sin βx
3.	f (x) = Acos βx +	корнем	1	1
3.	f (x) = Acos βx +	корнем	y = xr ( A cos βx +
	+Bsin βx	б) число iβ является	1
		корнем кратности r	+B1 sin βx)
		корнем кратности r

		а) число iβ не является	y = Qk cos βx +
4.	f (x) = Pn (x)cos βx +	корнем	+Mk sin βx, k = max(n,m)
	+R (x)sin βx	б) число iβ является	y = xr (Q cos βx +
	m	корнем кратности r	k
		корнем кратности r	+ Mk sin βx)

		а) число α +iβ не явля-	y = eαx[Qk cos βx +
5.	f (x) = eαx[Pn (x)	ется корнем	+Mk sin βx]
	cos βx + Rm (x)sin βx]	б) число α +iβ является	y = xreαx[Q cos βx +
		корнем кратности r	k
		корнем кратности r	+Mk sin βx]
			+Mk sin βx]

Здесь Q, R, M - многочлены с неопределенными коэффициентами.

13.5.2. Метод вариации произвольной постоянной

			c1′y1 + c2′y2 +…+ cn′ = 0,
			c1′y1′ + c2′y2′ +…+ cn′ = 0,
			c1′y1′ + c2′y2′ +…+ cn′ = 0,
yO.H . = c1(x) y1 + c2 (x) y2							…
yO.H . = c1(x) y1 + c2 (x) y2	+…+ cn (x)yn ,						…
		(n−2)			(n−2)		(n−2)		= 0,
		c1′y1		+ c2′y2			+…+ cn′yn		= 0,
		(n−1)		(n−1)		+	(n−1)	= f (x).
	c1′y1		+ c2′y2			+	…+ cn′yn	= f (x).

c1 = ∫c1′dx + c1, c2 = ∫c2′dx + c2 ,…cn = ∫cn′dx + cn .

!Если f (x) = f1(x) + f2 (x) +…+ fk (x) , то частное решение представляет сумму частных решений, соответствующих каждому слагаемому в правой части.

В результате изучения материала, изложенного в этих лекциях, студенты должны знать:

основные понятия и методы решения ОЛДУ и НЛДУ;

специальные методы решения ОЛДУ и НЛДУ с постоянными коэффициентами.

Лекция 14 СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

В лекции рассмотрены системы дифференциальных уравнений (ДУ) и методы их решения. Особое внимание уделено линейным системам с постоянными коэффициентами, которые возникают при решении многих задач механики и электротехники.

14.1. Основные понятия 14.2. Метод исключения неизвестных 14.3. Линейные системы ДУ

14.4. Однородные системы линейных ДУ с постоянными коэффициентами

14.5. Неоднородные системы линейных ДУ с постоянными коэффициентами

14.1. Основные понятия

ОСистема n ДУ первого порядка с n неизвестными функциями x1, x2 ,..., xn от одной переменной t вида

x′	= f (t, x ,..., x ),
1	1	1	n
′	= f2 (t, x1,..., xn ),
x2	= f2 (t, x1,..., xn ),
..............................

′	= fn (t, x1,..., xn ),
xn	= fn (t, x1,..., xn ),

называется нормальной системой обыкновенных ДУ.

ООбщим решением системы называется совокупность n функций от t и n произвольных постоянных:

x	= x (t,c ,c ,...,c ),
1	1	1	2	n
x2 = x2		(t,c1	,c2	,...,cn ),
..................................

x	= x	(t,c	,c	,...,c ),
n	n	1	2	n

которые удовлетворяют всем уравнениям системы.

!Любая система ДУ может быть приведена к нормальному виду. Пусть, например, система состоит из n уравнений порядка m :

Системы дифференциальных уравнений

321

(m)

′

′′

(m−1)

′

(m−1)

′

(m−1)

, x2

,...,x2

, ..., xn

,...,xn

= f1 (t,x1 ,x1 ,x1 ,...,x1

,x2

,xn

(m)

′

′′

(m−1)

, x2

′

(m−1)

, ..., xn

′

(m−1)

= f2 (t,x1 ,x1

,x1 ,...,x1

,x2

,...,x2

,xn

,...,xn

..............................

(m)

= f

(

′

′′

(m−1)

, x

′

,...,x

(m−1)

, ..., x

′

,...,x

(m−1)

)

t,x ,x ,x ,...,x

1 1 1

Переобозначим функции: x1,0

= x1 , x2 ,0 = x2 , ..., xn ,0

= xn и введем допол-

нительные:

′

x1,2

′′

(m−1)

x1,1 = x1 ,

= x1 , ..., x1,m−1 = x1

x2 ,1 = x2′, x2,2 = x2′′, ..., x2,m−1 = x2(m−1),

.....................................................

xn ,1 = xn′ , xn,2 = xn′′, ..., xn ,m−1 = xn(m−1).

x′

В новых обозначениях уравнения системы принимают вид:

= x

1,0

11,

′

= x1,2 ,

x1,1

...............

x1′,m−2 = x1,m−1 ,

,x11, ,x1,2 ,...,x1,m−1 ,x2,0 ,x2,1 ,...,x2,m−1 ,...,xn,0 ,xn,1 ,...xn,m−1 ),

x1′,m−1 = f1 (t,x1,0

′

= x2,1 ,

x′

= x

...............

′

,m−2 = x2,m−1 ,

x2′

,m−1 = f2 (t,x1,0 ,x11,

,x1,2 ,...,x1,m−1 ,x2,0 ,x2,1 ,...,x2,m−1 ,...,xn,0 ,xn,1 ,...xn,m−1 ),

.......................................................................................................................

′

= xn,1 ,

xn ,0

′

= xn ,2 ,

xn ,1

...............

′

xn ,m−2 = xn,m−1 ,

,m−1 = f2 (t,x1,0 ,x11,

,x1,2 ,...,x1,m−1 ,x2,0 ,x2 ,1 ,...,x2,m−1 ,...,xn,0 ,xn ,1 ,...xn ,m−1 ).

xn′

Вместо системы n уравнений порядка m получена нормальная система из n ×m уравнений.

322

Лекция 14

14.2. Метод исключения неизвестных

Нормальная система n ДУ первого порядка сводится к одному ДУ n-го порядка методом исключения неизвестных. Проиллюстрируем этот метод решения на примерах.

Пример:

dx = y2 +sin t,

Найдите решение системы

dydt = 2xy .

Решение:

Продифференцируем первое уравнение:

d 2 x

+cos t ;

подставим

из второго уравнения:

d 2 x

= x + cos t ;

dt2

получим НЛДУ второго порядка для

x(t)

d 2 x

− x = cos t .

Его решение

= − 1 cos t ,

x = x + x , k 2 −1 = 0 , k = ±1 ,

x = c et

+c e−t ,

dx = c et

x = c et +c e−t

− 1 cos t ,

−c e−t + 1 sin t ,

= dx −sin t = c et −c e−t

− 1 sin t .

x = c et +c e−t

− 1 cos t,

Ответ:

= c et −c e−t − 1 sin t

1 2

В качестве примера решим систему уравнений второго порядка.

Пример:

2x = y,

Решите систему dt

d 2 y

= x.

Решение:

Дважды продифференцируем первое уравнение

d 2 y

d 4 x

dt4

подставим во второе d 4 x = x ,

x(4) − x = 0 , k 4 −1 = 0 ,

= ±1, k

3,4

= ±i .

dt4

1,2

x = c1et +c2e−t

+c3 cos t +c4 sin t,

Ответ:

+c e−t

−c

cos t −c sin t.

y = x′′ = c et

Системы дифференциальных уравнений

323

14.3. Линейные системы ДУ

Нормальная линейная система		ДУ с n	неизвестными функциями
x1, x2 ,..., xn от одной переменной t имеет вид:
x′	= a x + a x +... + a x + b ,
1	11 1 12 2	1n n	1
′	= a21x1 + a22 x2	+ + a2n xn	+ b2 ,
x2
...........................................................

′	= an1x1 + an2 x2	+ + ann xn	+ bn ,
xn

где коэффициенты aik и bi - известные функции t или постоянные, i,k =1,2,...,n .

ОСистема называется неоднородной, если хотя бы одна из функций bi (t)

(i =1,..., n) отлична от нуля для t (a,b) ; в противном случае система на-

зывается однородной.

14.4.Решение линейных однородных систем ДУ

спостоянными коэффициентами

x′	= a x + a x ...+ + a x ,
1	11 1 12 2	1n n
′	= a21x1 + a22 x2 + + a2n xn ,
x2	= a21x1 + a22 x2 + + a2n xn ,
..................................................

′	= an1x1 + an2 x2 + + ann xn .
xn	= an1x1 + an2 x2 + + ann xn .

14.4.1. Метод исключения неизвестных

Из уравнений системы, а также из уравнений, получающихся дифференцированием уравнений, входящих в систему, исключают все неизвестные (n- 1) функции, кроме одной xk , для которой получают одно ДУ более высокого

порядка: xk (n) + a1xk (n−1) + a2 xk (n−2) +... + an xk = 0 .

Интегрируя это уравнение, находят одну из неизвестных функций, а остальные (n-1) неизвестные функции определяются из исходных уравнений и уравнений, получившихся при дифференцировании, без интегрирования.

Рассмотрим однородную систему двух уравнений:

x′ = a11x + a12 y,

y′ = a21x + a22 y,

где x(t), y(t) - искомые функции, а aij - постоянные.

324

Лекция 14

Покажем, что эта система может быть сведена к ДУ второго порядка для

d 2 x

функции

x(t) . Продифференцируем первое

уравнение

dt2

= a11 dt + a12 y′,

′

d 2 x

подставим y

из второго уравнения, тогда

dt2

= a11 dt + a12

(a21x + a22 y) , отку-

да

d 2 x

−

(a + a )

+ (a a

− a a )x = 0 .

11 22

Это уравнение является ОЛДУ второго порядка с постоянными коэффи-

циентами, его характеристическое уравнение имеет вид:

k 2 − (a + a )k + (a a − a a ) = 0 ,

а решение x = x(t) зависит от корней характеристического уравнения.

Пример:

= ax + y,

Найдите решение системы: dy

= −x + ay,

Решение:

a = const.

Перепишем систему в других обозначениях:

x′ = ax + y,

где x′ =

dx ,

y′ =

dy .

y′ = −x + ay,

′′

′

+ y

′

Продифференцируем первое уравнение x

= ax

подставим значение y′

из второго уравнения,

тогда x′′−2ax′+(1+ a2 )x = 0 , k 2 + 2ak + (1 + a2 ) = 0 ,

откуда k = a ±i

и x(t) = eat (C1 cos t +C2 sin t ).

Из первого уравнения найдем

y = x′−ax = aet (C1 cos t +C2 sin t )+

+eat (−C1 sin t +C2 cos t )−aeat (C1 cos t +C2 sin t )= eat (−C1 sin t +C2 cos t ).

Ответ:

x(t) = eat (C1 cos t +C2 sin t ),

y(t) = eat (C2 cos t −C1 sin t ).

Пример:

x′ = 3x −2 y,

Найдите решение системы

Решение:

y′ = 3x −4 y.

′′

′

−2 y

′

= 3(3x −2 y) −2(3x −4 y) = 3x +2 y = 3x +3x − x

′

x = 3x

= 6x − x

x′′+ x′−6x = 0 , k2 +k −6 = 0 , k1 = 2 , k2 = −3 .

Корни действительные, разные.

y = 3x − x′ = C1 e2t +3C

x = C e2t +C e−3t ,

e−3t .

Системы дифференциальных уравнений

325

14.4.2. Непосредственное решение

Рассмотрим однородную систему трех ЛДУ с постоянными коэффициентами для трех неизвестных функций

x′ = a x + a y + a z,
	11	12	13
				(*)
y′ = a21x + a22 y + a23 z,				(*)

z′ = a31x + a32 y + a33 z.

Сформулируем некоторые общие свойства таких систем:

1. Если функции {x, y, z} являются решением системы, то функции {Cx,Cy,Cz}, где С – любое постоянное число, также являются решением системы.

2.Если {x1, y1, z1} и {x2 , y2 , z2} - решения системы, то {x1 + x2 , y1 + y2 , z1 + z2} являются решением системы.

Справедливость этих свойств устанавливается непосредственной подстановкой в систему.

3.Из вышеприведенных свойств следует, что если {x1, y1, z1}, {x2 , y2 , z2} и {x3 , y3 , z3} являются решениями системы, то их линейные комбинации

{C1x1 +C2 x2 + C3 x3 ,C1 y1 +C2 y2 +C3 y3 ,C1z1 +C2 z2 + C3 z3}	также	являются
решением системы.	x =αekt ,	y = βekt ,
Будем искать ненулевые решения системы (*) в виде:	x =αekt ,	y = βekt ,

z =γekt (**), где α, β,γ и k - некоторые числа, которые нужно подоб-

рать так, чтобы функции (**) удовлетворяли системе (*). Подставляя функции (**) и их производные в систему, получим:

= a11α e

+ a12 β e

+ a13γ

− k)α + a

β + a γ = 0,

β kekt = a21α ekt + a22 β ekt + a23γ ekt , ↔ a21α + (a22 − k)β + a23γ = 0,

γ kekt

= a α ekt

+ a β ekt

+ a γ ekt

a31α + a32 β + (a33 − k)γ = 0.

Получили однородную систему с тремя неизвестными α, β и γ . Для то-

го, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель системы был равен нулю. Таким образом, число k должно удовлетворять уравнению:

a11 − k	a12	a13
a11 − k	a12	a13
a21	a22 − k	a23	= 0 .
a31	a32	a33 − k

326 Лекция 14

Это уравнение называется характеристическим уравнением системы. Оно является уравнением третьего порядка относительно k . Имеет три корня k1, k2 и k3 . Каждому из этих корней соответствует ненулевое решение систе-

мы α1, β1,γ1 ; α2 , β2 ,γ2 ; α3 , β3 ,γ3 , а значит, и ненулевое решение исходной системы дифференциальных уравнений имеет вид:

				k1t					k1t						k1t
x1 =α1e				k1t	,	y1 = β1e			k1t	,		z1 =γ1e			k1t	,
x1 =α1e					,	y1 = β1e				,		z1 =γ1e				,
x2 =α2ek2t , y2 = β2ek2t , z2 =γ2ek2t ,
x		=α	ek3t , y				= β	ek3t , z			3	=γ	3	ek3t .
	3	3				3	3				3		3

Линейные комбинации этих функций с произвольными коэффициента-

ми:

x = C1α1ek1t + C2α2ek2t + C3α3ek3t ,y = C1β1ek1t + C2 β2ek2t + C3β3ek3t ,z = C1γ1ek1t +C2γ2ek2t + C3γ3ek3t ,

также будут решением системы.

Пример:

	x′ = x + 2 y,
Решите систему
	y′ = 4x +3y.
Решение:
Характеристическое уравнение имеет вид:
	1−k	2	= 0 , k 2 −4k −5 = 0 → k = 5, k		2	= −1.
	1−k	2	= 0 , k 2 −4k −5 = 0 → k = 5, k			= −1.
	4	3 −k		1
	4	3 −k

Корни характеристического уравнения действительные, разные. Решение ищем в виде: x =αe5t , y = β e−t .

При этом x′ = 5αe5t , y′ = −βe−t . Подстановка решения такого вида в исходную систему дает:

k = 5 :

(1−5)α + 2β = 0,

→ −4α +2β = 0 ,

β = 2α , коэффициент α ос-

4α +(3 −5)β = 0

тается произвольным. Полагая α = C

, получим

x = C e5t , y = 2C e5t .

k = −1

(1+1)α + 2β = 0,

→ 2α + 2β = 0,

β = −α , коэффициент α ос-

4α +(3 +1)β = 0

тается произвольным. При

α = C :

= C e−t

, y

= −C e−t .

Системы дифференциальных уравнений						327

		Общее решение имеет вид:	x = C1e5t +C2e−t ,
		Общее решение имеет вид:				e−t .
			y = 2C e5t −C			e−t .
				1	2
	Пример:
		x′ = y + z,
		Решите систему y′ = 3x + z,

		z′ = 3x + y.

Решение:

Ищем решение в виде x =αekt , y = βekt , z =γekt .

Система для нахождения неопределенных коэффициентов α, β и γ имеет вид:

−α	k + β +γ = 0,
		+γ = 0,
3α − β k
	+ β −γ	k = 0.
3α
Характеристическое уравнение:
−k 1 1

3	−k	1 = 0	, k3 −7k −6 = 0 , k = −1, k	2	= −2 , k	3	= 3 .
			1	2		3
3	1	−k

Корни характеристического уравнения действительные, разные. Подставим в систему для нахождения α, β и γ полученные значения k :

α + β +γ = 0,

k1 = −1: 3α + β +γ = 0,

откуда

α = 0,

β = −γ ,

- любое

число;

+γ = 0,

3α + β

если

γ =1, получим

x = 0

, y = −e−t

, z = e−t .

2α + β +γ = 0,

2α + β = −γ,

α = −γ,

β =γ ,

любое

= −2 : 3α + 2β +γ = 0,

2β = −γ,

+ 2γ =

3α +

3α + β

число; если γ =1, то

x = −e−2t , y

= e−2t ,

= e−2t .

−3α + β +γ = 0,

−3α + β = −γ ,

откуда β =γ ,

γ ,

= 3 : 3α −3β +γ = 0,

α =

3α −3β = −γ ,

3α + β −3γ = 0,

где γ

- любое число; если γ = 3 , то α = 2,

β = 3, γ = 3

x = 2e3t , y = 3e3t , z = 3e3t .

Общее решение системы принимает вид:

= −C2e−2t + 2C3e3t ,

= −C1e−t +C2e−2t +3C3e3t ,

= C e−t +C

e−2t +3C e3t .

328

Лекция 14

Пример:

x′ = x − y,

Решите систему

y′ = x +3y.

Решение: Характеристическое уравнение:

1−k

−1

= 0 , k 2 −4k +4 = 0 , k = k

= 2 .

3 −k

Корни характеристического уравнения действительные, равные.

Решение ищем в виде: x = (α + β t)e2t ,

y = (α

+ β

t)e2t .

Для него x′ = e2t (β1 + 2α1 + 2β1t),

y′ = e2t (α2 + β2 + β2t) .

Подстановка этих выражений в исходную систему дает два равносиль-

ных уравнения вида 2α1 + β1 + 2β1t =α1 + β1t −α2 − β2t .

= −β ,

Приравнивая коэффициенты в этом уравнении, получаем:

α2

=α1 − β1,

при этом коэффициенты α1

и β1 остаются произвольными.

Положим, α1 = C1, β1 = C2 , тогда общее решение имеет вид:

= (C1 +C2t )e

= −(C1 +C2

+C2t )e2t .

Пример:

Решите систему

x′

= −7x + y,

Решение:

y′ = −x −5y.

Характеристическое уравнение:

−7 −k

= 0, k 2 +12k +37 = 0 ,

k = −6 ±i .

−2

−5 −k

1,2

Корни характеристического уравнения комплексные. Ищем решение в

виде x =α ekt ,

y = β ekt .

Возьмем одно из комплексно-сопряженных

значений k = −6 + i :

(−7 +6 −i)α + β = 0,

−α −iα + β = 0,

−2α +(−5 +6 −i)β = 0,

−2α + β −iβ = 0,

уравнения равносильны, β =α(1+i) , α и

β остаются произвольными,

пусть, например,

β =1+i , тогда x = e(−6+i)t ,

y = (1+i)e(−6+i)t .

По формуле Эйлера

e(α+β i)t

= eα (cos t +i sin t) ,

поэтому

x = e−6t (cos t +i sin t) ,

y = (1+i)e−6t (cos t +i sin t) =

Системы дифференциальных уравнений

329

= e−6t (cos t −sin t) + ie−6t (cos t +sin t) .

За системы частных решений можно взять отдельно действительные и

отдельно мнимые части:

x = e−6t cos t ,

x = e−6t

sin t ;

= e−6t (cos t −sin t) , y

= e−6t (cos t +sin t) .

Этих функций достаточно, чтобы составить общее решение системы в

виде:

x = e

−6t

(C1 cos t +C2 sin t),

(cos t +sin t)].

y = e−6t [C (cos t −sin t) +C

Пример:

x′ = x −5y,

Решите систему

y′ = 2x − y.

Характеристическое уравнение

1−k

−5

= 0 , k 2 +9 = 0, k = ±3i .

−1−k

1,2

Воспользуемся k = 3i . Ищем решение в виде x =αe3it , y = βe3it , подстановка такого решения в исходную систему приводит к системе:

(1−3i)α −5β = 0,

β +3iβ −2α = 0,

двух равносильных уравнений, поэтому α и β остаются произвольны-

ми, так как β =α 1−53i , положим, например, α = 5 , β = 1 − 3i .

Следовательно,

x = 5e3it = 5(cos 3t +i sin 3t) , y = (1−3i)e3it = (1−3i)(cos 3t +i sin 3t) .

Действительная и мнимая части этого решения также являются решениями исходной системы, а их линейная комбинация с произвольными коэффициентами является общим решением:

x = 5C1 cos 3t +5C2 sin 3t,

y = C1 (cos 3t +3sin 3t) +C2 (sin 3t −3cos 3t).

14.4.3. Метод интегрируемых комбинаций

x′ = f (t, x, y),
Интегрирование некоторых систем вида	1	осуществляется
	f2 (t, x, y)
y′ =

путем подбора интегрируемой комбинации, т.е. дифференциального уравнения, являющегося следствием уравнений системы, но уже легко интегрирующегося.

330

Лекция 14

Пример:

dx = y,

Решите систему: dt .

dydt = x.

Решение:

Складывая почленно данные уравнения, получаем

d (x + y) = x + y,

d (x + y)

= dt, ln | x + y |= t +ln C

, x + y = C et .

x + y

Вычитая уравнения, получаем

d (x − y) = −(x − y) ,

d (x − y)

= −dt , ln | x − y |= −t +ln C

x − y = C e−t .

x − y

x + y = C1e

Из системы

e−t

получаем решение в виде:

x − y = C

x =

(C1et +C2e−t ),

(C1et −C2e−t ) .

Пример:

Решите систему:

(z − x)2

x −1

z −1

Решение:

x −

Составим интегрируемые комбинации:

z −1

d (z − x)

x − z

(z − x)2

(x −1)

= (z −1)

+ C1

(x −1)dx

= (z −1)dz,

откуда

(z − x)d (z − x) = −dy,

(z − x)2

−y +

Решением системы является линия пересечения поверхностей,

(x −1)

−(z −

= C1,

задаваемая системой:

− x)2 = C

2 y +(z

Системы дифференциальных уравнений

331

14.5.Неоднородные линейные системы ДУ с постоянными коэффициентами

Рассмотрим неоднородную систему:
x′+ a x + a y				= b (t),
		11	12	1

y′+ a21x + a22 y = b2 (t),
где bi (t) - известные функции, aij - постоянные,					x(t), y(t) - искомые функ-
ции.					x′′+ a11x′+ a12 y′ = b1′,
Продифференцируем по t первое уравнение:					x′′+ a11x′+ a12 y′ = b1′,
откуда	y′ = b1′− a11x′− x′′ ;
	y′ = b1′− a11x′− x′′ ;
			a12
из первого уравнения y = b1 − a11x − x′, подстановка во второе уравнение дает:
	a12
b1′− a11x′− x′′		+ a21x + a22		b1 − a11x − x′		= b2 ,
a12		+ a21x + a22		a12		= b2 ,
a12				a12
x′′+ (a11 + a22 )x′+ (a22a11 − a12a21)x = b1′+ a22b1 − a12b2					- уравнение 2-го порядка с
одной неизвестной функцией x(t) .
Интегрируя это уравнение, получаем x = f1(t,C1,C2 ) , подставляя это вы-

ражение и его производную в первое уравнение, найдем вторую искомую функцию y = f2 (t,C1,C2 ) .

Пример:

x′+ 2x + y = sin t,

Найдите решение системы

y′ = 4x + 2 y +cos t,

если x

= 2,

=1.

Решение:

′′

′

+ y

′

= cos t ,

подставляя в

Продифференцируем первое уравнение: x

+2x

′

−2x

из первого уравнения, получим x

′′

= −2 sin t .

него x = sin t − y

Характеристическое уравнение k2 = 0 имеет решение k

= k

= 0 .

x = x + x ,

x = C1

+C2t , x ищем в виде x = A sin t + B cos t ,

тогда x′ = A cos t − B sin t , и x′′ = −Asin t − B cos t = −2 sin t ,

откуда A = 2 , B = 0 ,

x = 2 sin t .

Решение имеет вид: x = C1 +C2t + 2sin t .

При этом x′ = C2 + 2 cos t и

y = sin t − x′−2x = sin t −(C2 + 2cos t) −2(C1 +C2t + 2sin t) =

332 Лекция 14

= (−2C1 −C2 ) −2C2t −3sin t −2cos t.

Итак, общее решение системы ДУ имеет вид:

x = C1 +C2t + 2sin t , y = −2C1 −C2 −2C2t −3sin t −2cos t .

Найдем частное решение из начальных условий:

= 2,

C +C

+ 2 =

+C2

2 2

−2C

−C

− 2C

−3 =1,

−2C −C

+π) = 4,

= 0,

C +C

2 2

C1 = −2π, C2 = −4 .

2C +C

(π +1) = −4,

Тогда

x = 2π −4t + 2sin t,

+8t −3sin t −2cos t.

y = −4π + 4

В результате изучения материала, изложенного в этих лекциях, студенты должны знать:

основные понятия и методы решения произвольных систем ДУ;методы решения однородных и неоднородных систем линейных ДУ

с постоянными коэффициентами.

Лекции 15 - 16 ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Во многих случаях функциональная зависимость не может быть сведена к функции одной переменной и приходится рассматривать функции, зависящие от нескольких аргументов. Основные особенности анализа таких функций удобно рассмотреть на примере функций двух переменных: этот случай легко интерпретируется геометрически и содержит все основные отличия, возникающие при переходе от одной к нескольким переменным.

15.1.Основные понятия

15.2.Предел функции двух переменных

15.3.Непрерывность функции двух переменных

15.4.Частное и полное приращения функции двух переменных

15.5.Частные производные первого порядка функции двух переменных

15.6.Полный дифференциал функции

15.7.Частные производные высших порядков

15.8.Дифференциалы высших порядков

15.9.Формула Тейлора

15.10.Производная сложной функции. Полная производная

15.11.Инвариантность формы полного первого дифференциала

15.12.Производная от функции, заданной неявно

16.1.Локальные экстремумы функции двух переменных

16.2.Условный экстремум. Метод множителей Лагранжа

16.3.Наибольшее и наименьшее значения функции в области

16.4.Геометрические приложения функций двух переменных

16.4.1.Производная векторной функции скалярного аргумента

16.4.2.Уравнение касательной к пространственной кривой

16.4.3.Нормальная плоскость и ее уравнение

16.4.4.Касательная плоскость и нормаль к поверхности

15.1.Основные понятия

ОЕсли каждой точке на плоскости или паре значений двух независимых переменных величин M (x, y) D соответствует определенное число z , то говорят, что на множестве D определена функция двух переменных

z= f (x, y) = f (M ) .

ОМножество точек (x, y) D значений независимых переменных x и y , при которых функция z имеет определенное действительное значение, называется областью определения функции двух переменных.

334	Лекции 15 - 16

Например,

1)площадь прямоугольника S = xy , x, y > 0 ;

2)объем параллелепипеда V = xyz , x, y, z > 0 ;

3)дальность полета тела, брошенного под углом α к горизонту со скоро-

стью υ : l =	υ2 sin 2α		0,	π	, υ > 0 .
стью υ : l =	g	, α	0,		, υ > 0 .
	g			2

Геометрически область определения функции двух переменных может быть изображена на плоскости (x, y) областью D с границей L , точ-

ка M1 D , M1 L – внутренняя, а M2 L – граничная точка области.

y	M 2

D M1

ООбласть определения называется замкнутой, если ей принадлежат все точки границы.

Пример:


Областью определения функции z = 4 − x2 − y2	y
является множество точек, определяемое неравенст-		x
вом 4 − x2 − y2 ≥ 0 , и представляет собой замкнутую	0	x
область: x2 + y2 ≤ 4 - внутренность круга с радиусом	0	2
область: x2 + y2 ≤ 4 - внутренность круга с радиусом
2 и центром в точке (0,0) , включающую границу об-
ласти.

Пример:

Областью определения функции z =	1
	x2 + y2 − 4 явля-	y

ется незамкнутое множество x2 + y2 −4 ≥ 0 , которое и		2 x
представляет собой внешность круга без точек грани-		0

цы.

Геометрическое изображение функции двух переменных

Функция z = f (x, y) определяет в про-

странстве поверхность S , проектирующуюся на плоскость Oxy в область определения D .

M ( x, y, z) S

0	y

N ( x, y,0) D

Функции нескольких переменных

335

Пример:

Поверхность, задаваемая ра-

венством z = sin x2 + y2 .

x2 + y2

15.2. Предел функции двух переменных

Пусть z = f (x, y) ,

(x, y) D , M 0 (x0 , y0 ) D .

Множество точек, удаленных от точки M 0

не больше, чем на r , называ-

ется

r −окрестностью

точки

M 0 ,

задается

неравенством

(x − x0 )2

+ (y − y0 )2

< r 2

геометрически

представляет

открытый

круг

радиусом r

с центром в точке M 0 .

Число A называется пределом функции f (x, y) = f (M )

в точке M 0

при

стремлении точки

M к точке M 0 ,

если для ε > 0 найдется такое

r ,

что

f (x, y) − A

< ε

(

f (М) − A

< ε )

при всех ( x, y ), принадлежащих r

окрестности точки M 0

x − x0

< r ,

y − y0

< r .

A = lim f (x, y) = lim

f (M ) .

x→x0

M →M 0

y→y0

Пример:

lim

3x + 4

0 + 4 =

4 .

x2 + y2

−1

x→0

4 −1 3

y→2

Пример:

Выясните, имеет ли функция z =

2xy

предел при x → 0 , y → 0 .

x2 + y2

Решение:

Пусть точка M (x, y)

стремится к точке M 0 (0,0) .

Рассмотрим изменение x и y вдоль прямой y = kx .

Получим, что lim z = lim

2kx2

x2 + k 2 x2

+ k 2

x→0

y→0

Результат имеет различные значения в зависимости от выбранного k ,

т.е. зависит от пути приближения к (0,0) , и поэтому функция не имеет

предела в точке (0,0).

336	Лекции 15 - 16
15.3. Непрерывность функции двух переменных

О Функция f (x, y) называется непрерывной в точке (x 0 , y 0 ) , если предельное значение этой функции в точке M 0 существует и равно частно-

му значению f (x0 , y0 ) : lim f (x, y) = f (x0 , y0 ) .
		x→x0
		y→y0
Для непрерывности		f (M ) в точке M 0 необходимо выполнение следую-
щих условий:
1)	f (M ) определена в точке M 0 и вблизи нее;
2)	предел f (M )	при стремлении точки M к точке M 0 произвольным

способом;

3)M →M 0 f (M ) = f (M 0 ) .

ОФункция f (M ) , непрерывная в каждой точке области D , называется

непрерывной в этой области.lim

О	Функция		f (M )	разрывна в точке M 0 , если не выполняется какое-либо
	из условий непрерывности.
	из условий непрерывности.
	Например, функция z = x2 + y2 – непрерывна на всей плоскости xОy ;
функция z =			2xy	не определена в точке (0,0) , которая является точкой
функция z =		x2 + y2		не определена в точке (0,0) , которая является точкой
		x2 + y2

разрыва. Разрыв не устраним, так как предел функции z в точке (0,0) не существует.

15.4. Частное и полное приращения функции двух переменных

Пусть z = f (x, y) , (x, y) D .

ОДадим переменной x приращение ∆x , оставляя переменную y неизменной, тогда разность ∆x z = f (x + ∆x, y) − f (x, y) называется частным

приращением f (x, y) по	x , а разность ∆y z = f (x, y + ∆y) − f (x, y) – ча-
стное приращение z по	y . Полное приращение функции z = f (x, y)

равно ∆z = ∆f (x, y) = f (x + ∆x, y + ∆y) − f (x, y) .

Пример:

Для функции z = x y частные приращения равны:

∆x z = (x + ∆x) y − xy = ∆x y ; ∆y z = x ∆y ;

полное приращение равно:

∆z = ( x + ∆x)( y + ∆y) − xy = ∆x y + x ∆y + ∆x ∆y = ∆x z + ∆y z + ∆x ∆y .

Видим, что ∆z ≠ ∆x z + ∆y z .

Функции нескольких переменных

337

15.5.Частные производные первого порядка функции двух переменных

Частной производной по x от функции z = f (x, y)

называется предел

∆x z

(x + ∆x, y) − f (x, y)

′

∂z

′

∂f (x, y)

lim

= lim

= f

(x, y)

∆x

∂x

∆x→0

Аналогично:

∆y z

′

∂z

′

∂f ( x, y )

f ( x,y + ∆y ) − f ( x,y )

= f

( x, y ) =

lim

= lim

∂y

∆y

∆y→0

Пример:

z = x3 sin y + y4 .

∂z

= 3x2 sin y ;

∂z

= x3 cos y + 4 y3 .

∂x

∂y

Геометрический смысл частных производных

Пусть z = f (x, y) , M поверхно-

сти S .

Положим y = const . Кривая Гx есть се-

чение поверхности S плоскостью, параллельной плоскости Oxz.

MK – касательная к кривой Гx в точке M ( x, y,z ), а угол, который она составляет с осью Ox , равен α .

∂z	dz	y = const ,	∂z	= tgα .
∂x	=		∂x

	dx

Итак, частная производная ∂∂xz численно

равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z = f ( x, y ) плоскостью

y = const . Аналогично ∂∂yz = tgβ .

α K

y y

Γx

β y

K ′

338 Лекции 15 - 16

15.6. Полный дифференциал функции

Пусть z = f ( x, y ) , тогда полное приращение функции равно

∆z = f (x + ∆x, y + ∆y) − f (x, y) .

	′
Рассмотрим две точки: M ( x, y ) и M ( x + ∆x, y + ∆y ) , отстоящие друг от дру-
га на расстоянии ρ =	( ∆x )2 + ( ∆y )2 .
Устремим точку M ′	к точке M , при этом ρ → 0 .

О Если при ρ → 0 можно подобрать не зависящие от ∆x и ∆y величины A и B так, что выражение ( A ∆x + B ∆y ) будет отличаться от ∆z на величину более высокого порядка малости по сравнению с ρ , то оно называется главной линейной частью полного приращения функции

∆z = A ∆x + B ∆y +γρ , где γ → 0 при ρ → 0 ( ∆x → 0, ∆y → 0 ).

ОДифференциалы независимых переменных равны их приращениям: dx = ∆x , dy = ∆y .

ОПолным дифференциалом z = f ( x, y ) называ-

ется главная линейная часть полного приращения функции: dz = A∆x + B∆y , где A, B − const .

Например, для z = xy геометрически проиллю-

∆y	∆z
y	dz
	x	∆x
	x

стрируем разницу между ∆z и dz .

∆z =( x + ∆x )( y + ∆y ) − xy = y∆x + x∆y + ∆x ∆y = dz + ∆x∆y ,

так как dz = ydx + xdy – главная (большая) линейная часть приращения функции.

ТДифференциал функции равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных.

Доказательство:

Пусть z = f ( x, y ) . По определению dz = A∆x + B∆y , а ∆z = A∆x + B∆y +α∆x + β∆y , где α, β – бесконечно малые при ∆x → 0 и

∆y → 0 .

Положим ∆y = 0 , тогда ∆x z = A∆x +α∆x , откуда					∆x z	= A +α .
Положим ∆y = 0 , тогда ∆x z = A∆x +α∆x , откуда					∆x	= A +α .
	∆x z	= ∂z			∆x
Устремим ∆x → 0 , тогда lim	∆x z			= A .
Устремим ∆x → 0 , тогда lim				= A .
∆x→0	∆x		∂x
Аналогично: B = ∂z , значит,	dz =		∂z dx + ∂z dy .
∂y			∂x	∂y

Функции нескольких переменных					339
	Если	z = f (x, y)	обладает	непрерывными частными производными
О	Если	z = f (x, y)	обладает	непрерывными частными производными
	∂z = f y′(x, y) и ∂z		= f y′(x, y)	в данной области, то она дифференцируема
	∂z = f y′(x, y) и ∂z		= f y′(x, y)	в данной области, то она дифференцируема
	∂x	∂y
	в этой области.
	Геометрический		смысл	полного дифференциала	функции
z = f (x, y) :		dz в точке (x0 , y0 ) изображается приращением аппликаты точки
касательной плоскости, проведенной к поверхности z = f (x, y)					в точке
M 0 (x0 , y0 ) .

Пример:

Найдите дифференциал функции z = x y .

dz = ∂∂xz dx + ∂∂yz dy , так как ∂∂xz = yx y−1 , ∂∂yz = x y ln x ,

то dz = yx y−1dx + x y ln xdy .

С точностью до бесконечно малых более высокого порядка: ∆z ≈ dz .

Значит, f (x + ∆x, y + ∆y) ≈ f (x, y) + ∂f (x, y) ∆x + ∂f (x, y) ∆y .

∂x ∂y

Это равенство используется в приближенных вычислениях.

Пример:

Вычислите приближенное значение (2,01)2,02 .

Функция имеет вид: z = x y . Из приближенного равенства

z(x

+ ∆x, y

+ ∆y) ≈ z(x

, y

) +

∂z

∆x +

∂z

∆y

∂x

( x0

, y0 )

∂y

( x , y

)

при x0 = 2 ,

y0 = 2 , ∆x = 0,01,

∆y = 0,02 получаем z(x0 , y0 ) = 22 = 4 ,

∂z

= yx y−1 ,

∂z

= 2 2 = 4 ;

∂x

(2,2)

∂z

= x y

ln x ,

∂z

= 22 ln 2 ,

∂y

(2,2)

получаем

(2,01)2,02 ≈ 4 + 4 0,01+ 4ln 2 0,02 = 4(1,01+0,02ln 2) = 4,04 +0,08ln 2 .

340 Лекции 15 - 16

15.7. Частные производные высших порядков

Частные производные первого порядка от функции двух переменных

z = f (x, y) , равные	∂z	= f x′(x, y) и	∂z	= f y′(x, y) , в свою очередь являются
	∂x		∂y

функциями переменных x и y , и от них можно снова находить частные производные второго порядка:

∂2 z

∂

∂z

= f ′′(x, y) ;

∂2 z

∂

∂z

= f ′′(x, y) ;

∂x

∂y

∂x

∂y

∂2 z

∂ ∂z

′′

∂2 z

∂

∂z

′′

( x, y) .

∂x∂y

fyx (x, y) ;

∂y∂x

fxy

∂x

∂y

∂x

ОДве последние производные по разным переменным называются сме-

шанными.

ТЕсли функция f (x, y) определена в области D , в которой существуют

′

′′

и смешанные производные

′′

производные f x ,

fy ,

fxx

, f yy ,

fxy , f yx

fxy и

f yx′′ непрерывны в точке (x0 , y0 ) D , то смешанные производные не за-

висят от

порядка

дифференцирования,

т.е.

равны друг другу:

f xy′′(x0 , y0 ) = f yx′′(x0 , y0 ) .

Запомним эту теорему.

Пример:

z = x y ,

x > 0 .

∂z

= y xy−1 ;

∂2 z

= yx y−1 ln x + x y−1 ;

∂x

∂y∂x

∂z

= x

ln x ;

∂2 z

= yx

y−1

ln x + x

y−1

, значит,

∂

2 z

∂2 z

∂y

∂x∂y

∂y∂x

Пример:

z = y ln x .

∂z

;

∂z

= ln x ,

∂2 z

∂ y

= −

∂2 z

∂

(ln x)= 0 ,

∂x

∂y

∂x2

∂x x

∂y2

∂y

∂2 z

∂ y

∂y∂x

∂y

Функции нескольких переменных

341

Пример:

Вычислите производную восьмого порядка

∂8 z

функции

∂y

∂x

z = x2 + x + x3 + 2x4 + x7 y9 + y10 .

Последовательно вычисляем:

∂z

= x

9 y

+10 y

;

∂2 z

= 9

+10 9 y

;

∂y

∂3 z = 9 8 7x7 y6

+10 9 8y7 ;

∂4 z

= 9 8 7 7x6 y6 ;

∂x∂y3

∂y3

∂5 z

= 9 8 7 7

;

∂6 z

9 8 7 7 6 5x

;

∂x2∂y3

∂x3∂y3

∂7 z

= 9 8 7 7 6 5 4x3 y6 ;

∂x4∂y3

∂8 z

= 9 8 7 7

6 5 4 3x2 y6 =

7 9! x2 y6 .

∂x5∂y3

15.8. Дифференциалы высших порядков

Пусть z = f (x, y) , (x, y) D .

В предположении о существовании непрерывных частных производных второго порядка вычислим дифференциал d 2 z второго порядка функции z как дифференциал первого порядка от дифференциала функции dz при условии, что dz является функцией только x и y . При вычислении дифферен-

циала

от

считаются

постоянными,

при

вычислении

дифференциала от

∂z

и ∂z

приращения x и y берутся равными dx и dy .

∂x

∂y

∂z

dx +

∂z

= d (dz) = d

= d dx + d

dy =

∂x

∂y

∂x

∂y

= ∂2 z dx2

∂2 z

dxdy +

∂2 z dy 2 +

∂2 z

dydx =

∂x∂y

∂x2

∂y 2

∂y∂x

∂2 z dx2

∂2 z

dxdy +

∂2 z dy 2

, где dx2

= (dx)2 , dy 2

= (dy)2 .

∂x∂y

∂x2

∂y 2

Итак,

d 2 z =

∂2 z dx2

∂2 z

dxdy +

∂2 z dy 2 .

∂x∂y

∂x2

∂y 2

342

Лекции 15 - 16

Использование символа d =

∂

dx +

∂

dy позволяет записать d 2 z как резуль-

∂x

∂y

тат действия этого оператора на z в виде: d

∂

2 z =

dx +

z .

∂x

∂y

Аналогично:

d 3 z = d (d 2 z) = d (d (dz))=

∂

d n z = d (d n−1 z)=

∂

dx +

z ,

dx +

dy z .

∂x

∂y

∂x

∂y

Пример:

Найдите d 2 z , если z = sin xy .

Решение:

d 2 z

∂2 z

(dx)2

+ 2

∂2 z

dxdy +

∂2 z

(dy)2 ,

∂z

= cos xy y ,

∂z

= cos xy x ,

∂x∂y

∂y 2

∂x

∂y

∂x2

∂2 z

= −sin xy y 2

∂2 z = − sin xy x 2 ,

∂2 z

= −sin xy xy + cos xy ,

∂x∂y

∂x

∂y 2

d 2 z = −y 2 sin xydx 2 + 2(cos xy − xy sin xy)dxdy − x2 sin xydy 2 .

15.9. Формула Тейлора

По аналогии с функцией одной переменной формула Тейлора для двух переменных имеет вид:

f ( x, y ) = f ( x , y

) +

df ( x

, y

) +

d 2

f ( x , y

) + ....+

d n f ( x0 , y0 ) + o (ρn (x, y;x0 , y0 )).

Пример:

Записать формулу Тейлора для функции z = e xy

в окрестности точки P(1,1)

до членов 1-го порядка включительно.

Вычисляем частные производные f (x, y) = e xy

в точке (1,1), получаем:

= e +

e[( x −1) + ( y −1)] +

e[( x −1)

( y −1)

+ 2( x −1)( y −1)]

e[ 1+θ( x−1 )][ 1+θ( y−1 )] .

15.10. Производная сложной функции. Полная производная

Рассмотрим сложную функцию z = F (u,υ) , где u = ϕ(x, y) , υ =ψ (x, y) ,

т.е. z = F[ϕ(x, y),ψ (x, y)].

Пусть функции F(u,υ) , ϕ(x, y) , ψ (x, y) имеют непрерывные частные производные по всем своим аргументам.

Функции нескольких переменных

343

Вычислим ∂z

и ∂z

. Дадим x приращение ∆x

при постоянном y , тогда

∂x

∂y

u примет значение u + ∆x u , а υ примет значение υ + ∆xυ .

Полное приращение функции z

принимает вид:

∆z =

∂F

∆

u +

∂F

∆ υ +α∆

u + β∆ υ ,

∂u

∂υ

где α, β – бесконечно малые функции при ∆x → 0 .

∆z =

∂F

∆x u

∂F

∆xυ

+α

∆x u

+ β

∆xυ

∂υ ∆x

∆x

∂u ∆x

∆x

Устремим ∆x к нулю, при этом ∆x u → 0 и ∆xυ → 0 в силу непрерывно-

сти

u и υ .

Так

как

lim

∆z =

∂z ,

lim

∆x u

∂u

lim

∆xυ

= ∂υ ,

∂x

∆x

∆x→0

∆x

∂x

∆x→0

∆x

∆x→0

∂x

limα = lim β = 0 , то ∂z = ∂F

∂u

+ ∂F

∂υ .

∆x→0

∂x

∂u

∂x

∂υ

∂x

Аналогично:

∂∂yz = ∂∂Fu ∂∂uy + ∂∂Fυ ∂∂υy .

Пример:

z = ln(u2 +υ), u = ex+y2 , υ = x2 + y .

Вычислим ∂∂xz и ∂∂yz .

∂z

;

∂u

u2 +υ

∂υ

∂u

= ex+y2

∂u = 2 yex+y2 ;

∂x

∂y

∂υ

= 2x ,

∂υ

=1 ;

∂x

∂y

(u ex+y2

+ x);

∂z

ex+y2 +

2x =

∂x

u2 +

+υ

∂z

2 yex+y2

(4uyex+y2 +1).

∂y

u2 +

+υ

Полная производная

Пусть z = F (x, y) , где y = f (x) .

∂F

∂x

∂F ∂y

, т.е.

∂F

∂y ∂x

∂x ∂x

∂x

∂y dx

344							Лекции 15 - 16
Если z = F (x, y) , где x = x(t) , y = y(t) , то	dz	=	∂F dx	+	∂F	dy	.

	dt		∂x dt
	dt		∂x dt		∂y dt

15.11. Инвариантность формы полного первого дифференциала

Пусть z = F (u,υ) , где u = u(x, y) , υ =υ(x, y) . Покажем, что форма первого дифференциала не меняется и dz = zu′du + zυ′dυ .

Действительно,

dz = z′x dx + z′y dy = (zu′u′x + zυ′υ′x )dx + (zu′u′y + zυ′υ′y )dy =

=zu′(u′x dx + u′y dy)+ zυ′(υ′x dx +υ′y dy)= zu′ du + zυ′ dυ .

15.12.Производная от функции, заданной неявно

Уравнение F (x, y) = 0 неявно задает функцию одной переменной

y= y(x) .

ТЕсли F(x, y) и ее частные производные Fx′(x, y) и Fy′(x, y) определены и

непрерывны в некоторой области,

содержащей точку (x, y) , F (x, y) = 0

и Fy′(x, y) ≠ 0 , то y′x = −

Fx′(x, y)

Fy′(x, y)

Доказательство:

Пусть F (x, y) = 0 . Дадим x

приращение ∆x , тогда y

примет значение

y + ∆y .

По условию F (x + ∆x, y + ∆y) = 0 , следовательно,

полное при-

ращение ∆F = F (x + ∆x, y + ∆y) − F (x, y) = 0 , значит

по

определению

∆F :

∂F

∆x +

∂F

∆y +α∆x + β∆y = 0 , где α, β – бесконечно малые функ-

∂x

∂y

ции при ∆x, ∆y → 0 .

Тогда

∂F

∂F ∆y

+α + β ∆y = 0 .

∂y ∆x

∂x

∆x

Отсюда

∂F

∆y = −

∂x

+α

∂F

∆x

∂y

+ β

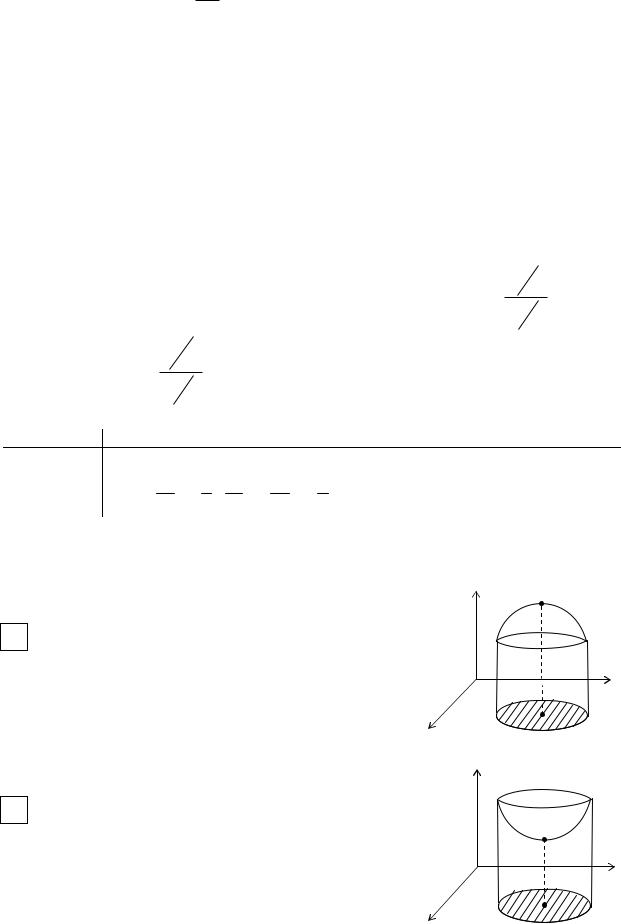
Функции нескольких переменных

345

При ∆x → 0 : α, β → 0 ; ∂∂Fy ≠ 0 по условию, и

dy		∂F		Fx′(x, y)
dy	= −	∂x	= −	Fx′(x, y)	( )
dx	= −	∂F	= −	Fy′(x, y)	( )
dx		∂F		Fy′(x, y)
		∂y

Рассмотрим уравнение F(x, y, z) = 0 . Оно неявно определяет функцию двух переменных z(x, y) . Найдем ∂∂xz и ∂∂yz .

При отыскании ∂∂xz считаем y постоянным, поэтому применима формула ( ) ,

∂F

если зависимой переменной считать x , а функцией – z : z′x = − ∂F ∂x .

∂z

∂F

Аналогично: z′y = − ∂F ∂y .

∂z

Пример:

Если x2 + y2 + z2 − R2 = 0 .

∂∂xz = − 22xz = − xz ; ∂∂yz = − 22yz = − yz .

16.1. Локальные экстремумы функции двух переменных

Функция z = f (x, y) имеет локальный максимум в точке M 0 (x0 , y0 ) , если для всех точек (x, y) , близких к M 0 , выполняется неравенство f (x0 , y0 ) > f (x, y) .

zmax = f (x0 , y0 )

Оz = f (x, y) имеет локальный минимум в

точке M 0 (x0 , y0 ) , если f (x0 , y0 ) < f (x, y) для всех точек (x, y) , близких к M 0 .

zmin = f (x0 , y0 )

x	M0 (x0 , y0 )
	z

M0(x0, y0 )

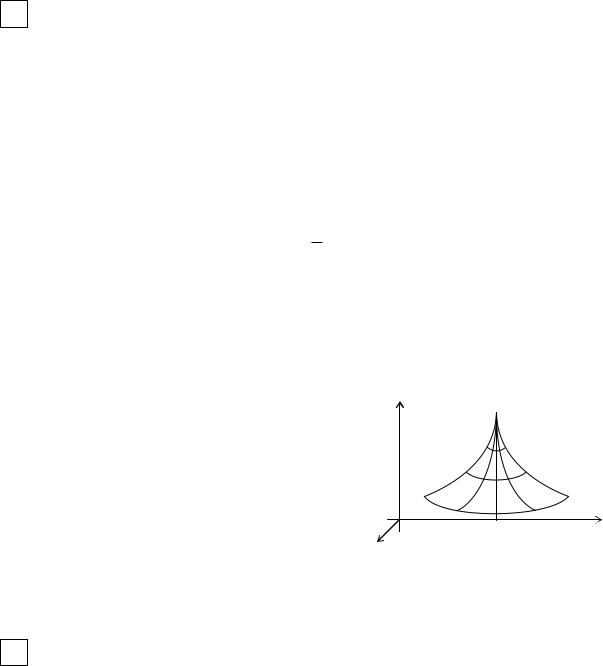
346	Лекции 15 - 16

ТНеобходимые условия экстремума. В точке экстремума функции двух переменных ее частные производные первого порядка либо равны нулю, либо не существуют.

Доказательство:

Пусть z = f (x, y) имеет максимальное значение f (x0 , y0 ) . Зафиксируем y = y0 , получим функцию одной переменной z1 = f (x, y0 ) ,

которая имеет максимум при x = x0 .
Из		теории	экстремума	функции	одной	переменной
	dz1	= f x′(x0 , y0 ) = 0 или не существует.
	dz1
	dx
		x=x0
		x=x0

Аналогично: f y′ = (x0 , y0 ) = 0 или .

В случае минимума доказательство аналогично. В точке экстремума M 0 (x0 , y0 ) дифференцируемой функции f (x, y) производные не суще-

fx′(x0 , y0 ) = 0;

ствуют или равны нулю: fy′(x0 , y0 ) = 0.

О	Точки, в которых частные произ-
	водные первого порядка некоторой			z
	водные первого порядка некоторой			z
	функции равны нулю или не суще-
	ствуют, называются критически-
	ми.
Геометрический смысл заключается в				y
том,	что	в точке M 0 , лежащей выше	x	M 0 ( x0 , y0 )
том,	что	в точке M 0 , лежащей выше	x
(ниже)		всех соседних, поверхность

z = f (x, y) либо имеет горизонтальную касательную плоскость, либо не имеет никакой касательной плоскости.

ТДостаточные условия экстремума. Пусть в некоторой области, содер-

жащей точку M 0 (x0 , y0 ) , функция z = f (x, y) имеет непрерывные ча-

стные производные до второго порядка включительно.							f (x, y) , т.е.
Пусть точка	M 0 (x0 , y0 ) является			критической точкой			f (x, y) , т.е.
∂f (x0 , y0 ) = 0 ,	∂f (x0 , y0 ) = 0 .
∂x	∂y
Введем обозначения: ∂2 f (x0 , y0 )			= A,		∂2 f (x0 , y0 )	= B , ∂2 f (x0 , y0 )		= C .
Введем обозначения: ∂2 f (x0 , y0 )			= A,			= B , ∂2 f (x0 , y0 )		= C .
	∂x2				∂x∂y		∂y 2
Составим дискриминант ∆ =		A	B	= AC − B 2 .
Составим дискриминант ∆ =		A	B	= AC − B 2 .
		B	C

Тогда:

Функции нескольких переменных

347

1) если ∆ > 0 , то функция имеет экстремум в точке (x0 , y0 ) , причем это максимум при A < 0 и минимум при A > 0 ;

2)если ∆ < 0 , то экстремума нет;

3)если ∆ = 0 , то требуется дополнительное исследование. Доказательство:

По формуле Тейлора второго порядка

f (M ) = f (M 0 ) + df (M 0 ) + 21!d 2 f (M 0 ) + R2 (M ) .

В критической точке

f ′(x0 , y0 ) = f y′(x0 , y0 ) = 0 ,

df (x0 , y0 ) = f x′(x0 , y0 )dx + f y′(x0 , y0 )dy = 0 ,

f(x, y) − f (x0 , y0 ) = ∆f (x0 , y0 )

иформула Тейлора принимает вид:

∆f (x

, y

) =

d 2 f (x

, y

) + R (x, y) .

Остаточный член R2 (x, y) является бесконечно малой более высокого

порядка,

чем d 2 f (x0 , y0 ) ,

поэтому знак

∆f (x0 , y0 ) совпадает со знаком

d 2 f (x , y

) в окрестности точки (x

, y

) .

Исследуем знак d 2 f (x0 , y0 ) :

d 2 f (x0 , y0 )

∂2 f (x0 , y0 )

dx2

+ 2

∂2 f (x0 , y0 )

dxdy +

∂x2

∂x∂y

∂2 f (x0 , y0 )

dy 2

= Adx2 + 2Bdxdy + Cdy 2 =

∂y 2

+ 2B

+ C

= dy2 A

Выражение в квадратных скобках является квадратным трехчленом с дискриминантом D = 4B2 − 4AC = −4∆.

1). Если ∆ > 0 , то D < 0 и знак квадратного трехчлена совпадает со знаком старшего коэффициента A , значит, знак d 2 f (x0 , y0 ) и, следовательно, знак ∆f (x0 , y0 ) совпадает со знаком A , то есть

а) если A < 0 , ∆f (x0 , y0 ) < 0 и (x0 , y0 ) – точка максимума; б) если A > 0 , ∆f (x0 , y0 ) > 0 и (x0 , y0 ) – точка минимума.

2). Если ∆ < 0 , то D > 0 и знак квадратного трехчлена меняется в окрестности точки (x0 , y0 ) и функция f (x0 , y0 ) не имеет экстремума в точке

(x0 , y0 ) .

348	Лекции 15 - 16
3). Если ∆ = 0 , то D = 0 и достаточный признак не дает ответа, нужно
выяснить сохраняется ли знак разности	∆f (x0 , y0 ) = f (x, y) − f (x0 , y0 ) непо-
средственно.

Схема исследования f ( x, y) на экстремум:

1)определите критические точки;

2)проанализируйте выполнение достаточных условий;

3)вычислите zэкстр. .

Пример:
Исследуйте на экстремум функцию z = x2 − xy + y2 +3x −2 y +1.
1) ∂z = 2x − y +3		,	∂z	= −x + 2 y −2 .
1) ∂z = 2x − y +3		,	∂y	= −x + 2 y −2 .
∂x			∂y
2x − y + 3 = 0,
	− 2 = 0,
− x + 2 y	− 2 = 0,
откуда x0	= − 4 ;	y0 =		1 .
	3			3

2) A =

∂2 z

= 2 , B

∂2 z

= −1 , C =

∂2 z

= 2 ,

∂x

∂x∂y

∂y2

−

;

−

;

−

;

∆ = AC − B2 = 2 2 −(−1)2 = 3 .

Итак, ∆ > 0

A > 0

;

, значит, −

– точка минимума, zmin = −

Пример:

Исследовать на экстремум функцию z = x

+ xy +1 .

∂z

2xy

+ x

+ y = 0,

∂x

z(0,0) =1.

1).

x0 = y0 = 0 ;

∂z

2 yx

+ y

+ x = 0

∂x

2). A = ∂2 z

=2y2 +1

=1; B =

∂2 z

= 4xy +1

=1;

∂x

(0,0)

∂x∂y

(0,0)

∂2 z

C =

= 2x2 +1

=1;

∂y

(0,0)

1 1

(0,0)

∆ = AC − B2 =

= 0 .

Достаточный признак ответа не дает. Исследуем значения z(x, y) .

z(x, y) = x

+ xy +1 =

(xy)

(x + y)

+1 , значит z(x, y) >1 ,

если x ≠ 0 ,

y ≠ 0 .

Получили, что z( x, y) > z(0,0) =1, значит,

(0,0) – точка минимума.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.11.201947.16 Кб2Лекции по бухгалтерской отчетности.doc
#
14.02.2015692.22 Кб33Лекции по ВССиТ.doc
#
16.09.2019877.06 Кб20Лекции по деревянным конструкциям.doc
#
14.02.201539.01 Mб49Лекции по истории.rtf
#
14.02.20152.87 Mб1608Лекции по коллоидной химии.pdf
#
14.02.20159.7 Mб918Лекции по математике.pdf
#
11.09.2019160.26 Кб1Лекции по социологии_на печать.doc
#
03.08.201954.95 Кб13Лекции по статистике.docx
#
14.02.2015147.88 Кб13Лекции по экономике.docx
#
14.02.20156.17 Mб59лекции.doc
#
14.02.20151.07 Mб339ЛЕКЦИи.doc