Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции по математике.pdf

Скачиваний:

918

Добавлен:

14.02.2015

Размер:

9.7 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1615 16 > Следующая >>>

Функции нескольких переменных																						353
				x	2

		y =				,

			2
			2							dz										1		1
			3			4		3		dz	= 3x	3	−3x	2	= 0 → x1					1		1
	2.3)	z =			x		− x		,	dx						= 0 ,	x2 =1,	z6	= 1,		= −		.
	2.3)	z =	4		x		− x		,							= 0 ,	x2 =1,	z6	= 1,	2	= −	4	.
			4																	2		4
		x	[0,2],


	3). Сравнивая полученные значения z , находим
	zнаим. = z(1,1) = −1 ,									zнаиб. = z(0, 2) =12 .

16.4. Геометрические приложения функций двух переменных

16.4.1. Производная векторной функции скалярного аргумента

K	JJJJG	G	G	G	G		z
r	= OM	, r	= xi	+ yj	+ zk .
Пусть проекции вектора r						являются функциями
параметра t :					x = x(t),
					x = x(t),
							O
					y = y(t),		O

					z = z(t),
тогда rG		= x(t)iG + y(t) Gj + z(t)kG				, rG = rG(t) .	x

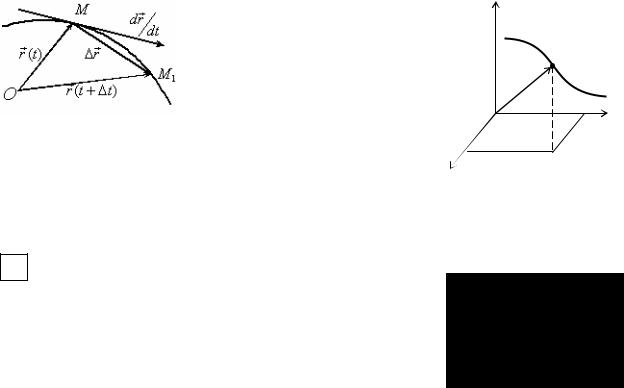
При изменении t изменяются проекции и конец вектора в пространстве линию, называемую годографом вектора.

M (x, y, z)

JJJJG

OM описывает

ОУказанные уравнения называются парамет-

рическимиG G уравнениями линии в пространстве. r = r (t) является векторной функцией

скалярного аргумента.

Найдем производную векторной функции скалярного аргумента.

Возьмем фиксированное значение t , соответствующее точке M на кривой и значению r (t) .

Дадим t приращение ∆t , получим вектор r (t + ∆t) , соответствующий

точке M1 .

Тогда

∆rG = rG(t + ∆t) − rG(t) = [x(t + ∆t) − x(t)]i +[y(t + ∆t) − y(t)] Gj +[z(t + ∆t) − z(t)]k ,

∆rG = rG(t + ∆t) − rG(t) =

354

Лекции 15 - 16

= [x(t + ∆t) − x(t)]iG +[y(t + ∆t) − y(t)] Gj +[z(t + ∆t) − z(t)]kG,

lim

∆rK

dx K

dy K

drK

;

∆t

i +

∆t

→0

∆rG(t)

x(t + ∆t) − x(t) G

y(t + ∆t) − y(t)

z(t + ∆t) − z(t)

j +

∆t

– вектор производной вектора r (t)

по скалярному аргументу t .

Выясним его направление. При ∆t → 0 точка M1

стремится к точке M , а на-

правление секущей MM 1

в пределе дает направление касательной, т.е. вектор

drG

направлен по касательной к кривой в точке M .

16.4.2.Уравнение касательной к пространственной кривой

1.Если линия задается параметрическим уравнением Gr = Gr(t) , то уравнение касательной к кривой r (t) в точке M 0 (x0 , y0 , z0 ) записывается как

уравнение прямой, проходящей через точку M 0 параллельно вектору								dr	.
Направляющий						вектор касательной {x − x0 , y − y0 , z − z0} и		dt	M0

								вектор
drG		dx	,	dy	,	dz	параллельны.

		=

dt	M0	dt		dt		dt M0

Условие параллельности заключается в том, что компоненты этих векторов пропорциональны, эти равенства и представляют уравнение каса-

тельной:

x − x0

y −

z −

M 0

2. Пусть кривая в пространстве задана как линия пересечения двух по-

верхностей:

Φ ( x, y,z ) = 0,

где x = x(t) ,

y = y(t) ,

z = z(t) .

L : 1

Итак,

Φ2 ( x, y,z ) = 0,

[x( t ), y( t ),z( t )] = 0,

Φ2 [x( t ), y( t ),z( t )]= 0.

Функции нескольких переменных								355
Продифференцируем эти уравнения:
	∂Φ dx	+	∂Φ dy		+	∂Φ dz		= 0,
	1		1	dt		1	dt
	∂x dt		∂y			∂z
	∂Φ2 dx	+ ∂Φ2 dy			+ ∂Φ2 dz = 0.

	∂x dt		∂y	dt		∂z	dt

Получим систему двух уравнений с тремя неизвестными dxdt , dydt , dzdt .

Найдем решение системы:

∂Φ1

∂x

∂Φ2

∂x

dxdt + ∂∂Φy1 dydt = −∂∂Φz1 dzdt , dxdt + ∂∂Φy2 dydt = −∂∂Φz2 dzdt .

dx	=		∆	1	,


По формулам Крамера dt			∆
dy		=	∆	2	,
			∆
dt

	∂Φ1 ∂Φ1
	∂Φ1 ∂Φ1
где ∆ =	∂x		∂y	,
	∂Φ		∂Φ
	2	2
	∂x		∂y

∂Φ1

∂Φ ∂Φ

∆ = − dz

∂z

∂y

= dz

∂y

∂z

= − dz

= dz

, ∆

∂x

∂z

∂x

∂Φ2

∂z

∂y

∂z

∂x

∂z

∂x

Итак,

∂Φ1

∂y

∂z

∂x

∂Φ2

∂Φ

∂y

∂z

;

∂z

∂x

∂Φ1

∂x

∂y

∂x

∂y

∂Φ2

∂x

∂y

∂x

∂y

356	Лекции 15 - 16

Решение может быть записано в виде:

∂Φ

∂y

∂z

∂x

∂y

∂Φ

∂Φ2

∂Φ

∂z

∂x

∂y

∂z

∂x

∂y

Подставляя выражения для

в уравнение касательной *), получим

его в виде:

x − x0

y − y0

z − z0

Φ′

1 y

Φ2′y

Φ2′z

Φ2′x

Φ2′y

если хотя бы один из определителей не равен нулю. Если все определители равны нулю, то точка называется особой точкой кривой.

16.4.3. Нормальная плоскость и ее уравнение

ОПрямая, перпендикулярная к касательной и проходящая через точку касания, называется нормалью к кривой в данной точке.

Множество нормалей к кривой лежит в плоскости, перпендикулярной к касатель-

ной и образует нормальную плоскость.

Уравнение плоскости, которая перпендикулярна касательной к кривой имеет вид уравнения плоскости, проходящей через

точку (x , y

, z

)

с нормальным вектором

M 0

а) в случае параметрического задания:

(x − x0 ) +

( y − y0 ) +

(z − z0 ) = 0 ;

M 0

б) если кривая задана как линия пересечения двух поверхностей:

Φ1′y Φ1′z

( x − x ) +

Φ1′z Φ1′x

( y − y

) +

Φ1′x

Φ1′y

( z − z

) = 0 .

Φ2′y Φ2′z

Φ2′z Φ2′x

Φ2′x

Φ2′y

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1615 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.11.201947.16 Кб2Лекции по бухгалтерской отчетности.doc
#
14.02.2015692.22 Кб33Лекции по ВССиТ.doc
#
16.09.2019877.06 Кб20Лекции по деревянным конструкциям.doc
#
14.02.201539.01 Mб49Лекции по истории.rtf
#
14.02.20152.87 Mб1608Лекции по коллоидной химии.pdf
#
14.02.20159.7 Mб918Лекции по математике.pdf
#
11.09.2019160.26 Кб1Лекции по социологии_на печать.doc
#
03.08.201954.95 Кб13Лекции по статистике.docx
#
14.02.2015147.88 Кб13Лекции по экономике.docx
#
14.02.20156.17 Mб59лекции.doc
#
14.02.20151.07 Mб339ЛЕКЦИи.doc