Примеры числовых множеств:

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции по математике.pdf

Скачиваний:

918

Добавлен:

14.02.2015

Размер:

9.7 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Лекции 8 – 9

Числа вида

: m

, n

образуют множество рациональ-

= q =

ных чисел.

Если

< n ,

то

рациональная

дробь называется правильной, если

m≥ n – неправильной.

!Рациональные дроби представляются в виде конечных или бесконечных периодических десятичных дробей после деления числителя на знаменатель.

Пример:

13 = 0,333... = 0,(3) , 52 = 0, 4 = 0,3999... = 0,3(9) ,

997 = 0,0707... = 0,(07) .

ОЧисла, выражающиеся бесконечной непериодической десятичной дробью, составляют множество иррациональных чисел I . Например,

2=1,41... , π = 3,14159265359..., e = 2,71828 18284 59045... .

ОРациональные и иррациональные числа составляют множество действи-

тельных чисел = I .

!Между множеством действительных чисел и множеством точек числовой прямой существует взаимно-однозначное соответствие.

8.3. Числовые промежутки

Показать, что функция y = x2 непрерывна в произвольной точке

ственной оси.

∆y = (x0 + ∆x)2 – x02 = x02 + 2x0 ∆x + ∆x2 – x02 = 2x0 ∆x + ∆x2.

lim ∆y = lim (2x0 ∆x + ∆x2 )= 2x0

lim ∆x + lim ∆x lim ∆x = 2x0 0 + 0 0 = 0.

Множество элементов x:

Элемент множества:

Отрезок (сегмент):

Интервал:

Полуинтервал (полусегмент):

Луч:

{x}

x{x}

{x} =[a,b]: a ≤ x ≤b, где a {x},b {x}

{x}= (a,b): a < x < b

{x} = (a, b]: a < x ≤ b,{x} =[a, b): a ≤ x < b,

{x} =[a, ∞) : (x ≥ a)

{x} = (−∞, b]: (x ≤ b)

Элементы теории множеств и математической логики. Числовые последовательности

Окрестность точки c - это произвольный интервал (a,b), содержащий точку с.

Эпсилон – окрестность точки с. {x : x − c <ε}

или c −ε < x < c + ε .

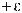
8.4. Ограниченные множества

ОМножество {x} называется ограниченным сверху, если существует такое число М, что x {x}: x ≤ M , где М называется верхней гранью множества {x} (ВГ {x}).

Пример:

{−1, 2,3, 4,5}, M1 = 5, M2 = 6, M3 =10,....

ТОграниченное сверху множество имеет бесконечное число верхних граней.

ОНаименьшая из всех верхних граней называется точной верхней гранью x = Sup{x} (от латинского supremum - наивысшее) (ТВГ {x}).

Пример:

{−1, 2,3, 4,5}, x = 5 .

ОМножество {x} называется ограниченным снизу, если существует такое число m, что x {x}: x ≥ m , где m – нижняя грань {x} (НГ {x}).

ТОграниченное снизу множество имеет бесконечное число нижних граней.

ОНаибольшая из всех нижних граней называется точной нижней гранью

x= Inf {x} (от латинского infimum - наинизшее) (ТНГ {x}).

О Множество {x} называется ограниченным, если существует число М > 0 такое, что x {x}: x ≤ M . Ограниченное множество является одновременно ограниченным и снизу, и сверху.

ОМножество {x}называется неограниченным, если для любого сколь угодно большого числа М > 0 найдется элемент x {x}, удовлетворяющий неравенству: x ≥ M .

96	Лекции 8 – 9

Пример:

Неограниченные множества:

(-∞,∞) – неограниченное множество, (-∞,2] – неограниченное снизу множество, [-5,∞) - неограниченное сверху множество.

!Для того чтобы множество было неограниченным, достаточно, чтобы оно было неограниченным либо сверху, либо снизу.

Число

называется

наибольшим

элементом

множества

{x},

M =max{x}, если 1) M {x}; 2) x {x}: x ≤M .

Число

называется

наименьшим

элементом

множества

{x},

m = min{x}, если 1) m {x}; 2) x {x}: x ≥ m .

Ограниченное сверху (снизу) множество может иметь наибольший (наи-

меньший) элемент, а может и не иметь его:

{x} =[a;b], max{x}=b, min{x} = a ;

{x} = (a;b),

max{x},

min{x} не существуют.

8.5. Числовые последовательности

Если каждому натуральному числу n по определенному закону постав-

лено

соответствие

некоторое

число

xn ,

то множество

x , x , x ,....x ,...

нумерованных чисел x , x , x ,.... называется чи-

{

{ 1 2

}

1 2

словой последовательностью. Элементы этого множества называются членами или элементами последовательности.

! Числовая последовательность может быть задана: 1) перечислением элементов;

2) заданием общего члена последовательности как функции номера xn = f (n);

3) в виде рекуррентных (возвратных) соотношений; в этом случае задается несколько первых членов последовательности и закон, по которому вычисляются последующие члены: xn+1 = f (xn ), x1 = const - одно-

членная рекуррентная формула, xn+2 = f (xn+1, xn ), x1 = c1, x2 = c2 - двучленная рекуррентная формула, и т.д.

Элементы теории множеств и математической логики. Числовые последовательности

Пример:

1){−1,1, −1,1,...}={(−1)n };

2)0, 1 , 2 ,... = n −1 ;2 3 n

3) {1, 2,3,...} = {n};

, n =1, 2,3,...;

n+1

2n−1

xn+2

= xn+1 + xn ,

x1 =1,

x3 = 2, x4 = 3,...

ОЕсли рассмотреть произвольную возрастающую последовательность натуральных чисел: k1,k2 , k3 ,....kn ,... и выбрать из последовательности {xn} ее члены с соответствующими номерами xk1 , xk2 ,...,xkn ,... то полученная по-

следовательность называется подпоследовательностью последовательности {xn}. Например, для произвольной последовательности подпосле-

довательностями являются последовательности четных или нечетных членов.

!Числовые последовательности являются упорядоченными числовыми множествами, для них справедливы теоремы об ограниченных множествах.

Пример:

Последовательность	{	n }	=	{	}	=	{	}
Последовательность		x	=		−n	=		−1, −2, −3,... −n,...	ограничена сверху,

поскольку все члены этой последовательности удовлетворяют неравенству xn ≤ −1.

Последовательность {xn } ={n2 } ограничена снизу, т.к. xn = n2 ≥1 .

Последовательность	1	ограничена. Для любого n N 0 <	1	≤1, т.е.
			n
n
M =1, m = 0 .

Пример:

Неограниченные последовательности:

1) {xn } ={n2 }. При любом M > 0 достаточно взять n > M .

2) {(1 − (−1)n )n}. Среди нечетных всегда найдется член, удовлетворяющий условию xn ≥ M для любого M > 0 .

98	Лекции 8 – 9

8.6.Свойства ограниченных последовательностей

1.Сумма двух ограниченных последовательностей есть последовательность ограниченная.

2.Разность двух ограниченных последовательностей есть последовательность ограниченная.

3.Произведение двух ограниченных последовательностей есть последовательность ограниченная.

!Неограниченные последовательности таких свойств не имеют.

9.1. Предел числовой последовательности

Конечное число a называется пределом числовой последовательности

}(обозначается

lim x

= a или

x → a ), если для любого положи-

n→∞

тельного числа ε

найдется такое натуральное число

N (зависящее от

ε ), что при всех n > N выполняется неравенство

xn − a

<ε .

Это может быть описано также в следующих терминах:

последовательность {xn } сходится к a ;

последовательность {xn } имеет предел, равный a ;

xn (общий член последовательности) стремится к a .

Сокращенная запись:

(nlim→∞ xn = a) ( ε > 0 N = N (ε ): n > N (ε )

xn − a

< ε ).

ОПоследовательность, имеющая конечный предел, называется сходящей-

ся.

!То же утверждение может быть сформулировано короче.

Число a есть предел последовательности {xn}, если ее члены отли-

чаются от a сколь угодно мало, начиная с некоторого места.

Исходное определение уточняет, как следует понимать «сколь угодно мало» и «начиная с некоторого места». ε > 0 xn − a < ε - точная

формулировка первого утверждения, а n > N (ε ) - второго.

Пример:

n −1		,	lim xn		= lim	n −1		−	1	= 1.
Дано: {xn }=		,	lim xn		= lim	n	= lim 1	−		= 1.
	n		n→∞		n→∞	n	n→∞		n
Докажем, что lim 1−			1	=1.
	n→∞		n

Доказательство:

Элементы теории множеств и математической логики. Числовые последовательности								99
ε > 0,	n −1 −1 < ε 1 −	1 − 1 < ε;	1	< ε, n >		1
	n	n	n			ε
Если взять N (ε )	– любое целое,	большее,		чем	1	,	то неравенство
					ε

n n−1 −1 < ε будет выполнено n > N (ε ), ч.т.д. Геометрическая интерпретация примера:

0		1	2		3		4		5	1
0	2									1
x1	2			3		4		5	6
x1	x		x3		x4		x5		x6
	2

− ε < x n − 1 < ε , 1 − ε < x n < ε + 1 .

ε =	1		1	= 2; n > 2	xn −1		<	1		.

		, N
	2		2					2
ε =	1		1	= 5; n > 5	xn −1	<		1	.

		, N
	5		5					5

!Последовательность {(−1)n} не имеет предела, так как нельзя указать

номер, после которого все члены последовательности окажутся в сколь угодно малой окрестности какого-либо числа.

ОПоследовательности, не имеющие предела, называются расходящими-

ся.

9.2.Бесконечно большие и бесконечно малые последовательности

ОПоследовательность {xn} называется бесконечно большой, если для

любого положительного числа M можно указать такое натуральное число N (зависящее от M ), что при всех n > N выполняется неравенство xn > M .

M > 0 N = N (M ): n > N (M ) xn > M .

ОЕсли числовая последовательность {xn} бесконечно большая и ее члены

(по крайней мере, начиная с какого-то номера) сохраняют определенный знак ( + или −), говорят, что последовательность {xn} имеет предел +∞

(или −∞ ): lim x	n	= +∞ ,	x	→ +∞ или lim x		n	= −∞ ,	x → −∞.
n→∞	n		n	n→∞	n→∞	n		n
				n→∞				n→∞

100	Лекции 8 – 9

Пример:

Последовательности {nα }, α > 0 , являются бесконечно большими, т.к.

для любого M > 0 из nα > M следует, что если n > α M , то условие определения выполнено.

ОПоследовательность {xn} называется бесконечно малой, если для лю-

бого сколь угодно малого положительного числа ε найдется такое натуральное число N (зависящее от ε ), что при всех n > N (ε) выполняется

неравенство xn <ε .

( ε > 0 N (ε ): n > N (ε ): xn < ε ).

! Из определения предела последовательности следует, что последова-

тельность {xn} бесконечно мала, если lim xn = 0 .

n→∞

Пример:

Бесконечно убывающая геометрическая прогрессия xn = qn , q <1, явля-

ется бесконечно малой последовательностью, т.к. для любого ε > 0 из неравенства q n < ε следует, что при n > log q ε это неравенство выпол-

нено, т.о. N (ε) = [log q ε].

9.3. Свойства бесконечно малых последовательностей

ТБесконечно малая последовательность ограничена.

Доказательство:

Пусть {xn} – бесконечно малая последовательность. Тогда для данного

ε, начиная с некоторого номера, имеет место неравенство xn <ε . Выбирая в качестве M максимальное из чисел ε, x1 , x2 ,..., xn −1 , получим xn < M для всех n , что и требовалось доказать.

ТСумма двух бесконечно малых последовательностей есть последовательность бесконечно малая.

ТРазность двух бесконечно малых последовательностей есть последовательность бесконечно малая.

ТПроизведение ограниченной последовательности на бесконечно малую есть последовательность бесконечно малая.

Элементы теории множеств и математической логики. Числовые последовательности

101

Доказательство:

Пусть {xn} – бесконечно малая, а {yn} – ограниченная последовательно-

сти, т.е. для любого ε > 0

существует N (ε) такое,

что для n > N (ε)

<ε , и существует такое число M , что для всех n

< M . Тогда для

последовательности {xn yn}

при n > N (ε) имеем

< ε M . Так как

M – фиксированное число, а ε – сколь угодно малое, то ε M также сколь угодно малое. Теорема доказана.

СПроизведение двух бесконечно малых последовательностей есть последовательность бесконечно малая.

Справедливость этого утверждения следует из того, что бесконечно малая последовательность всегда ограничена.

ТЕсли элементы бесконечно малой последовательности {xn} не равны

нулю, то последовательность будет бесконечно большой.

Т Если {xn} бесконечно большая последовательность и xn ≠ 0 , то после-

довательность – бесконечно малая.

Пример:

1). Последовательность

sin n

– бесконечно малая,

т.к. ее элементы яв-

ляются произведением

элементов

ограниченной

последовательности

{sin n} и бесконечно малой последовательности

2). Последовательность

n +1

– бесконечно малая, т.к. является суммой

бесконечно малых последовательностей

−n

3). Последовательность

– бесконечно малая, т.к. является произве-

дением бесконечно малой последовательности {e−n } на бесконечно малую

последовательность

Последовательность {xn}

называется фундаментальной, если для лю-

бого положительного ε > 0 найдется номер N (ε)

такой, что для всех n ,

удовлетворяющих условию n > N (ε),

и для всех натуральных чисел m

( m =1,2,3,...) справедливо неравенство

xn+m − xn

< ε.

ε > 0 N (ε) : n > N (ε) m N : xn+m − xn < ε .

102	Лекции 8 – 9

ТКритерий Коши. Для того чтобы последовательность {xn} была сходящейся, необходимо и достаточно, чтобы она была фундаментальна.

9.4. Свойства сходящихся последовательностей

1º. Элементы сходящейся последовательности имеют вид: xn = a +αn , где {αn} – бесконечно малая последовательность.

Доказательство:

По определению предела ε > 0 N (ε ): n > N (ε ), xn − a < ε .

Рассмотрим αn = xn − a xn = a +αn , подставим

a +αn − a < ε ε > 0 N (ε) : n > N (ε) αn < ε , т.е. limαn = 0 αn - бесконечно малая последовательность.

n→∞

2º.

3º.

Сходящаяся последовательность имеет только один предел. Доказательство:

Пусть a = lim xn и b = lim xn , a ≠ b , a < r < b – два предела сходящейся

n→∞ n→∞

последовательности {xn }.

ε > 0 N1 : n > N1 xn − a < r − a n > N1 xn < r ;ε > 0 N2 : n > N2 xn −b < b − r n > N2 xn > r .

Выберем N = N (ε )= max{N1 ,N2} и n ≥ N : тогда должно одновременно выполняться xn < r и xn > r , что невозможно, значит, a = b . Сходящаяся последовательность ограничена.

Обратное	утверждение неверно, например, последовательность
	πn	является ограниченной, но предела не имеет.
{xn} = sin		является ограниченной, но предела не имеет.
	2

4º. Сумма, разность, произведение			и также частное (при	условии, что
n	yn ≠ 0 и lim yn ≠ 0) двух сходящихся последовательностей {xn} и
	n→∞
{yn} есть сходящаяся последовательность, и ее предел равен соответст-
венно сумме, разности, произведению и частному пределов исходных
последовательностей.
Доказательство (сумма):
Пусть	{xn} и {yn} – сходящиеся последовательности			и lim xn = a ,
		yn = b + βn где {αn} и {βn}		n→∞
lim yn	= b . Тогда xn = a +αn ,	yn = b + βn где {αn} и {βn}		– бесконечно
n→∞			xn + yn = a +b +αn + βn , т.е. последова-
малые	последовательности,	и	xn + yn = a +b +αn + βn , т.е. последова-

тельность {xn + yn − a −b} – бесконечно малая, и поэтому {xn + yn} сходится и имеет своим пределом a + b .

Элементы теории множеств и математической логики. Числовые последовательности

103

САрифметические операции над сходящимися последовательностями приводят к таким же операциям над их пределами.

5º. Если элементы сходящейся последовательности {xn}, начиная с не-

	которого номера, удовлетворяют неравенству xn ≤ b ( xn ≥ b ), то и предел
	этой последовательности	lim xn	≤ a удовлетворяет	неравенству a ≤ b
	( a ≥ b ).	n→∞
	( a ≥ b ).
	1. Если элементы xn и yn	сходящихся последовательностей {xn} и {yn},
С	1. Если элементы xn и yn	сходящихся последовательностей {xn} и {yn},
	начиная с некоторого номера, удовлетворяют неравенству xn ≤ yn , то их
	пределы удовлетворяют такому же неравенству: lim xn ≤ lim yn .
			n→∞	n→∞
	2. Если все элементы сходящейся последовательности {xn}				находятся на
	отрезке [a;b], то и ее предел также находится на этом отрезке.
6º.	Пусть {xn} и {zn} – сходящиеся последовательности и lim xn = lim zn = a .
				n→∞	n→∞
	Пусть, начиная с некоторого номера, элементы последовательности {yn}
	удовлетворяют неравенствам		xn ≤ yn ≤ zn .Тогда	последовательность
	{yn} сходится и lim yn = a .
7º.	n→∞
7º.	Любая подпоследовательность сходящейся последовательности сходит-
	ся к тому же пределу.

9.5. Монотонные последовательности

ОПоследовательность {xn} называется неубывающей (невозрастающей), если каждый последующий член этой последовательности не

меньше (не больше) предыдущего, т.е. если для всех номеров n справедливо неравенство xn ≤ xn+1 ( xn ≥ xn+1 ).

ОНеубывающие и невозрастающие последовательности называются монотонными последовательностями.

ОЕсли вместо нестрогих неравенств xn ≥ xn+1 и xn ≤ xn+1 имеют место строгие неравенства xn < xn+1 или xn > xn+1 , то последовательности называют-

ся возрастающей и убывающей соответственно.

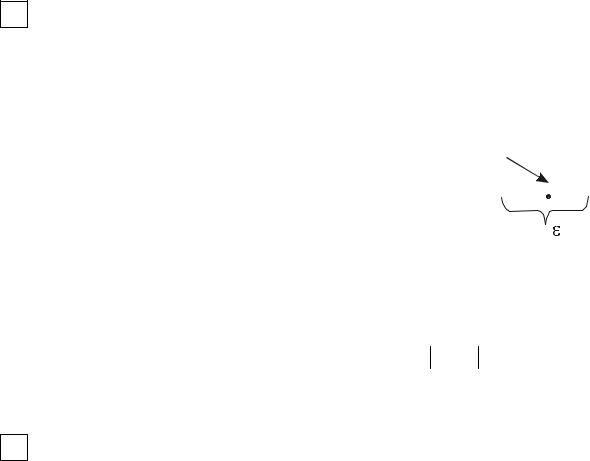
104

Лекции 8 – 9

Пример:

1). Последовательность {1,1, 2, 2,3,3, 4, 4,..., n, n,...}

- неубывающая.

– возрастающая, так как xn+1 > xn .

2). Последовательность

2 +1

Действительно,

(n +1)2

−

(n +1)2 (n2 +1)− n2 ((n +1)2 +1)

(

)

n +

2 +1

n2 +1

((n +1)

+1)(n

+1)

2n +1

> 0 .

((n +1)2 +1)(n2 +1)

3). Последовательность 1

– убывающая, так как

− x =

−

= −

< 0 .

n (n +1)

n+1

n +1

ТПризнак сходимости монотонной последовательности. Если неубывающая (невозрастающая) последовательность {xn} ограничена сверху (снизу), то она сходится.

Докажем, что если неубывающая последовательность ограничена сверху, то она сходится (имеет предел).

Доказательство:

{xn}- ограничена сверху {xn} имеет

x = Sup		{	x покажем, что lim x		= x .
		{	}	n→∞ n		x
1)	n, xn ≤ x ;			n→∞ n		x
1)	n, xn ≤ x ;
2)	ε > 0 найдется элемент xN > x −ε ,
n > N, xN ≤ xn				(по условию {xn}- неубываю-

щая), т.е. запишем последовательно:

x −ε < xN ≤ xn ≤ x x −ε < xn ≤ x

−x ≤ −xn < −x +ε 0 ≤ x − xn < ε xn − x <ε ,

то есть по определению предела x = lim xn .

n→∞

!1. Любая неубывающая последовательность всегда ограничена снизу первым элементом. Любая невозрастающая последовательность всегда ограничена сверху первым элементом.

2. Не всякая сходящаяся последовательность является монотонной.

Элементы теории множеств и математической логики. Числовые последовательности

105

Пример:

} ,

=1+

(−1)k

, lim x

, однако {x

} - немонотонная.

n→∞

ТНеограниченная монотонная последовательность является бесконечно большой.

9.6. Число е как предел монотонной последовательности

Рассмотрим последовательность {x	}, x	=	1	+	1 n .
n	n
					n

Исходя из признака сходимости монотонной последовательности, достаточно доказать, что:

1){xn} - является возрастающей;

2){xn} - ограничена сверху.

1+1 n

Из 1) и 2) делаем вывод о существовании предела .

Доказательство:

Воспользуемся формулой бинома Ньютона:

(a +b)

= anb0 + nan−1b1 +

n(n −1)

an−2b2

n(n

−

1)(n

−

n−3 3

(

n −

)(

− 2

)

...

(

−

(

)) 0 n

+...... +

1 n

n −1

a b ,

где n! =1 2 3 ... n .

Тогда

xn =

1 n

=1+ n

n(n −1) 1

n(n −1)...(n −(n −1))

+...

n −1

2 +

−

+... +

1−

−

... 1−

Аналогично для xn+1

xn+1

= 2 +

−

1−

+... +

n +1

106 Лекции 8 – 9

	1				1			2			n
+			1	−		1	−		... 1	−		,
	(n +				n +1			n +1			n +1
		1)!

1)	1 −	1	<	1 −	1	. Заметим, что x	содержит на одно положитель-

					n +1	n+1
		n
ное слагаемое больше, чем xn , следовательно n xn < xn+1 .
Таким образом, {xn}						– последовательность возрастающая

2)При n ≥ 2 0 < 1− 1 <1=> xn > 2 .

3)xn < 2 + 2!1 + 3!1 +... + n1! ; если заменить каждое слагаемое еще боль-


шим:	1	= 1	,	1		=	1		<		1		=	1		,... ,		1	<		1	,
шим:		= 1	,	3!		=	2 3		<		2 2		=	22		,... ,			<			,
	2! 2			3!			2 3				2 2			22				n! 2n−1
получаем: xn <								1		1			1				1
					2 +				+			+			+... +					.
					2 +			2	+	22		+	23		+... +		2n−1			.
								2		22			23				2n−1

{...} - сумма убывающей геометрической прогрессии, для которой

b =	1	, q =	1	,b =	1	, S =	b (1 − qn )	S =1−	1	;
							1

1	2		2	n	2n−1		1 − q		2n
	2		2		2n−1		1 − q		2n

n S <1 n xn <3.

Вывод: возрастающая последовательность {xn} ограничена сверху, следовательно, последовательность сходится.

		+	1 n
!			1 n
!	1. Обозначение lim 1		= e , 2 < e < 3 (Эйлер);
	n→∞		n
			e ≈ 2,7 1828 1828 459045...

2. Число e имеет большое значение в математическом анализе. y = ex - показательная функция с основанием e ;

y = ln x - натуральный логарифм (логарифм по основанию e ).

3. Справедливо утверждение: если {αn} – произвольная бесконечно малая последовательность и αn ≠ 0 , то

lim (1+αn ) 1 αn = e. n →∞

Элементы теории множеств и математической логики. Числовые последовательности

107

9.7. Предельные точки. Верхний и нижний пределы

ОТочка x бесконечной прямой называется предельной точкой числовой последовательности {xn }, если в любой ε -окрестности этой точки име-

ется бесконечно много элементов последовательности { xn }.

!Иногда предельная точка именуется точкой сгущения (что связано с геометрической интерпретацией действительных чисел как точек на числовой оси). Точки, представляющие собой члены последовательности, как бы «сгущаются» вблизи предельной точки.

Подобный «геометрический» подход позволяет высказать два утверждения, строгое доказательство которых опустим:

1)всякая сходящаяся последовательность имеет только одну предельную точку;

2)последовательность, имеющая несколько предельных точек, расходится.

Пример:

1). Последовательность { 1−(−1)n } имеет две предельные точки x = 0 и x = 2 , но не имеет предела.

2). Последовательность {e−n } имеет одну предельную точку x = 0, которая является одновременно пределом этой последовательности.

ТПринцип Больцано – Вейерштрасса. У всякой ограниченной последо-

вательности существует хотя бы одна предельная точка.

		Наибольшая предельная точка	последовательности		{xn}			называется
О		Наибольшая предельная точка	последовательности		{xn}			называется
		верхним пределом последовательности и обозначается					=		x .
		верхним пределом последовательности и обозначается				a	=	lim	x .
								n→∞ n
		Наименьшая предельная точка	последовательности		{xn}			называется
О		Наименьшая предельная точка	последовательности		{xn}			называется
		нижним пределом последовательности и обозначается a = lim xn .
							n→∞
	Пример:
		1). Последовательность 1, 1	, 1, 1 , ..., 1,	1
	2		3	n
		имеет верхний предел a = 1 и нижний предел a = 0 .
		2). Последовательность 1, 2, 3, 1, 2, 4, 1, 2, 5, ..., 1, 2, n, ....

имеет нижний предел a =1 , тогда как обычного предела у нее нет, поскольку она неограниченная.

108	Лекции 8 – 9

Сформулируем без доказательства теорему, показывающую важность

этих понятий (значения пределов в ней могут быть и несобственными числами, т.е. +∞ или −∞).

ТДля любой числовой последовательности верхний и нижний пределы всегда существуют. Их равенство есть условие, необходимое и достаточное для существования предела (в обычном смысле).

!Предел в обычном смысле также может оказаться несобственным числом.

В результате изучения материала, изложенного в этих лекциях, студент должен владеть следующими понятиями:

множество, элемент множества;

целые, натуральные, рациональные, действительные числа;

виды числовых множеств (интервал, сегмент, луч и т.п.);

ограниченные и неограниченные множества;

числовая последовательность, способы ее задания;

предел числовой последовательности;

бесконечно большие и бесконечно малые последовательности, их свойства;

свойства сходящихся последовательностей;

монотонные последовательности, признак сходимости монотонной последовательности;

предельная точка (точка сгущения) последовательности.

Лекции 10 - 11 ФУНКЦИИ. ПРЕДЕЛ ФУНКЦИИ

В лекциях 10 – 11 рассматривается одно из основных понятий математики – понятие функции. Обсуждаются способы задания функции, различные свойства функций, приводится классификация функций и, для справки, таблица основных элементарных функций с их графиками. Далее рассмотрено опорное для всего математического анализа понятие предела функции, приведены разновидности определений (определение по Коши и определение по Гейне, предел в точке и предел в бесконечности, односторонние пределы и т.п.). Заканчивается лекция описанием бесконечно малых и бесконечно больших функций - весьма удобного математического инструмента, широко использующегося в различных доказательствах.

10.1.Понятие функции. График функции. Способы задания функции

10.2.Основные характеристики функции

10.3.Обратная функция. Сложная функция

10.4.Основные элементарные функции

10.5.Элементарные и неэлементарные функции

11.1.Предел функции в точке

11.2.Предел функции в бесконечности

11.3.Односторонние пределы

11.4.Бесконечно малые и бесконечно большие функции и их свойства

11.5.Таблица определений предела

10.1.Понятие функции. График функции.

Способы задания функции

Понятие функции – одно из основных математических понятий, оно относится к установлению соответствия между элементами двух множеств.

ОЕсли задано правило f , по которому каждому элементу x из множества X поставлен в соответствие единственный элемент y из множества Y ,

то говорят, что на множестве X задана функция y = f (x), x X , y Y .

Множество X называется областью определения функции (ООФ) и

обозначается D( f ). Множество изменения функции Y называется об-

ластью значений функции (ОЗФ) и обозначается E ( f ).

В дальнейшем будем рассматривать (в основном) числовые функции, т.е. функции, у которых ООФ и ОЗФ Y являются числовыми множествами, X , Y . В этом случае переменная величина x называется независи-

мой переменной или аргументом, величина y - зависимой переменной

или функцией (от x). Число y , соответствующее данному значению x, назы-

вается частным значением функции в точке x.

110	Лекции 10 – 11

ОМножество точек (x, f (x)) плоскости Oxy называется графиком функции y = f (x).

Функция может быть задана: 1) аналитически; 2) графически; 3) с помощью таблицы.

При аналитическом задании функция может быть определена:

f		(x), x D	D( f )
	1	1		;
1) явно - уравнением вида y = f (x) или y =	f	(x), x D D( f )		;
	f	(x), x D D( f )
	2	2

2)неявно - уравнением вида F (x, y )= 0 ;

3)параметрически – с помощью вспомогательной переменной –

параметра – x = x(t ),

t T .

y = y (t ),

Пример:

Явное задание:

{ }

{

}

{ }

{

}

1). y = 1 − x2 ,

x =

x :

≤

1 ,

y =

y : 0

≤ y ≤1

;

y =

x ≥ 0,

2).

−x,

x < 0,

{x}={x : −∞ ≤ x ≤ ∞},{y}={y : 0 ≤ y ≤ ∞}

1, x > 0,

3). y = sgn x - знак x ,

sgn x = 0, x = 0,

−1, x < 0,

{x} ={x : −∞ ≤ x ≤ ∞}, {y} ={−1,0,1}

0, x −иррац.,

4). Функция Дирихле y =

1, x −рац.,

{x} ={x : −∞ ≤ x ≤ ∞},

{y}={0,1}.

5). y =[x]- целая часть x (наибольшее целое,

не превосходящее x )

D ( f )={x} ={x : −∞ ≤ x ≤ ∞},

E ( f )={y} ={y :целыечисла};

эта функция может быть задана в виде

...

1, x [1; 2),

[x]= 0, x [0;1), .

−1 x [−1; 0),

...

Функции. Предел функции

111

Неявное задание:

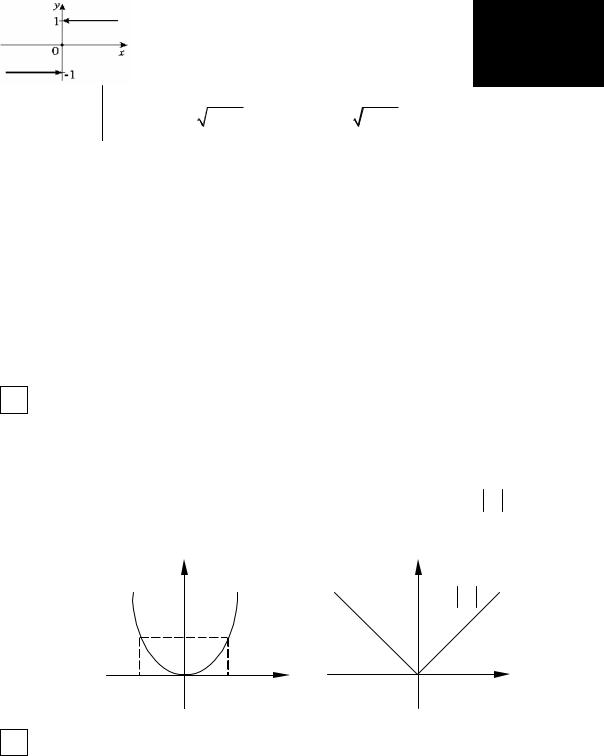
уравнение F (x, y)= 0 может определять не одну, а несколько функций вида y = f (x). Так, уравнение x2 + y2 −1 = 0 определяет две функции: y = f1 (x)= + 1 − x2 и y = f2 (x)= − 1 − x2 .

Аналитический способ задания функции является наиболее точным и предпочтительным для дальнейшего исследования функции методами математического анализа. Графическое и табличное описание возникает, например, при исследовании экспериментально наблюдаемых функциональных зависимостей, но и в этом случае обычно подбирают подходящую аналитическую формулу, с достаточной степенью точности воспроизводящую экспериментальные данные (так называемая аппроксимация).

10.2. Основные характеристики функции
О	Функция f (x)	с симметричной относительно нуля областью определе-
	ния X называется четной, если для				любого x X	выполняется равен-
	ство f (x) = f (−x).
	Из определения четной функции следует, что ее график симметричен
относительно оси ординат. Например, функции y = x2 ,						y = x являются чет-
ными, их графики имеют вид:
		y		y = x2	y
				y = x2	y = x
		y0
	–x0	0	x0	x	0	x

ОФункция f (x) с областью определения X называется нечетной, если для любого x X выполняется равенство f (−x) = − f (x).

График нечетной функции симметричен относительно начала координат. Например, функции y = x3 и y = 2x являются нечетными, их графики имеют вид:

112										Лекции 10 – 11
	y					y
			y = x3			y0		y = 2x
				x		–x0				x
		0		x			0	x0		x
							–y0
Функция y = x2 + x не является					ни четной,			ни	нечетной, так как

(−x)2 + (−x)= x2 − x ≠ ±y .

ОФункция y = f (x) называется периодической, если существует такое

число T ≠ 0 , что для любого x X выполнены условия: 1) x +T X ; 2) f (x +T )= f (x). Число T называется периодом функции y = f (x).

Множество значений числовой функции может быть ограниченным, ограниченным сверху (снизу) и неограниченным. В соответствии с этим под-

разделяются и сами функции.

О Функция f называется ограниченной на множестве E D( f ), если

A : x E f (x) ≤ A .

Например, функция y = sin (x) ограничена на всей числовой оси; y = x3 ограничена на любом промежутке конечной длины, но не ограничена на всей

	области определения x .
	Функция	f	называется ограниченной сверху (снизу) на множестве
О	Функция	f	называется ограниченной сверху (снизу) на множестве
	E D( f ), если A : x E f (x)≤ A ; ( A : x E						f (x)	≥ A ).
	E D( f ), если A : x E f (x)≤ A ; ( A : x E						f (x)	≥ A ).
	Например, y = x2			ограничена снизу на всей области определения x .
	Точная верхняя (нижняя) грань множества M значений функции f на
О
	E называется точной верхней (нижней) гранью функции f								на E и
	E называется точной верхней (нижней) гранью функции f								на E и
	обозначается sup f (x ) ( inf f (x)).
			x E		x E
			x E	1
	Например,		sup	1	= 0 , inf x2 = 0 .
		x (−∞;0)		x	x
	Если число		sup f (x) ( inf f (x)) принадлежит множеству M значений
О	Если число		sup f (x) ( inf f (x)) принадлежит множеству M значений
			x E		x E
					x E
	функции				то оно называется наибольшим (наименьшим) зна-
	функции	f	на E ,		то оно называется наибольшим (наименьшим) зна-
	чением f	на E и обозначается max f (x) ( min f (x)).
					x E	x E
Например, min x2 = 0 ,					max 1 не существует.
		x		x (−∞;0) x					( f ).
Пусть y = f (x) определена на множестве D( f ) и множество E D									( f ).

Функции. Предел функции				113
О Если x1, x2			E :
x1 < x2		f	(x1 )< f (x2 ) -	f (x) возрастающая на E ;
x1	< x2	f (x1 )≤ f (x2 ) -		f (x) неубывающая на E ;
x1	< x2	f (x1 )> f (x2 ) -		f (x) убывающая на E ;
x1	< x2	f (x1 )≥ f (x2 ) -		f (x) невозрастающая на E .

Все четыре типа в совокупности называются монотонными на E , а возрастающие и убывающие - строго монотонными на E .

10.3. Обратная функция. Сложная функция

О Функция y = f (x), x X , y Y обратима, если каждое свое значение она принимает один раз, то есть для каждого y Y существует только одно значение x X такое, что y = f (x).

ОТогда функции y = f (x), осуществляющей

отображение множества X в множество Y, может быть сопоставлена функция x = g (y),

осуществляющая отображение Y в X, такое, что g ( f (x))= x . Эта функция называется обратной к f (x) и обозначается f −1 (y).

С другой стороны, для функции x = f −1 ( y) обратной является функция y = f (x), поэтому функции y = f (x) и x = f −1 (y) называют-

ся взаимно обратными.

Графики функций y = f (x) и x = f −1 (y) совпадают, но если мы хотим описать функцию f −1 (y) обычным образом, то есть ее аргумент

обозначить через x , а зависимую переменную через y , то графическая иллюстрация изменится.

Вначале изменим направления осей; затем изменим названия осей; в результате получаем, что графики взаимно обратных функций симмет-

y	y = f (x)
y	x = f −1(y)
x	x

x = f −1(y)

y = f −1(x)

114				Лекции 10 – 11
ричны относительно биссектрисы первого и
третьего	координатных	углов, то	есть линии	−1(x)
y = x .				−1(x)
y = x .
Множество значений обратной функции
y = f −1 (x)	совпадает с	областью	определения	x

функции y = f (x), а область определения обратной функции y = f −1 (x) совпадает с множеством значений функции y = f (x).

Пример:

1) y = 1x = f (x), x (− ∞, 0) (0, ∞), y (− ∞, 0) (0, ∞);

g (x)= f −1 (x)= 1x (обратная функция совпадает с исходной).

2)		x	,	x > 0,	x (− ∞, 0) (0, ∞),
2)	y = f (x)= e		,	x > 0,	x (− ∞, 0) (0, ∞),
	− e x ,			x < 0,	y (−1,0) (1,∞);

y = f −1 (x)= ln x, x > 1,					x (−1, 0) (1, ∞),
	ln(− x), x (−1, 0), y (− ∞,0) (0,∞).

f и

Если

g -

функции

одного переменного,

то функция h ,

определенная

соотношением

h(x)= g f (x)

на

области

D(h)=

{

( f ):

}

x D

называется сложной функцией или

f (x) D(g )

суперпозицией (композицией) функций f и g и обозначается g f .

Операции производятся справа налево – вначале вычисляется частное значение функции f и в точке x , а затем для данного числа, рассматриваемого как аргумент, вычисляется значение функции g .

Операция суперпозиции может применяться повторно, например,

F (x)= lg sin (tg (x2 )) представляет собой суперпозицию пяти операций: возведение в квадрат, вычисление тангенса, синуса, модуля и логарифма.

Функции. Предел функции

115

10.4.Основные элементарные функции

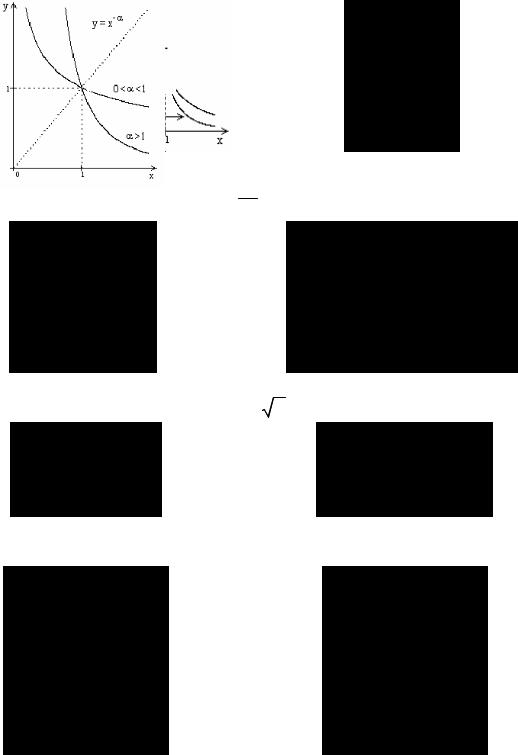
1.Степенные функции

1.1. y = xn , n N .

1.2. y = x1n , x ≠ 0 .

1.3. y = n x .

1.4. y = xα , α .

116	Лекции 10 – 11
2. Трансцендентные функции
2.1. Показательная	2.2. Логарифмическая
y = ax , a > 0, a ≠1.	y = loga x, a > 0, a ≠1, x (0,∞) .

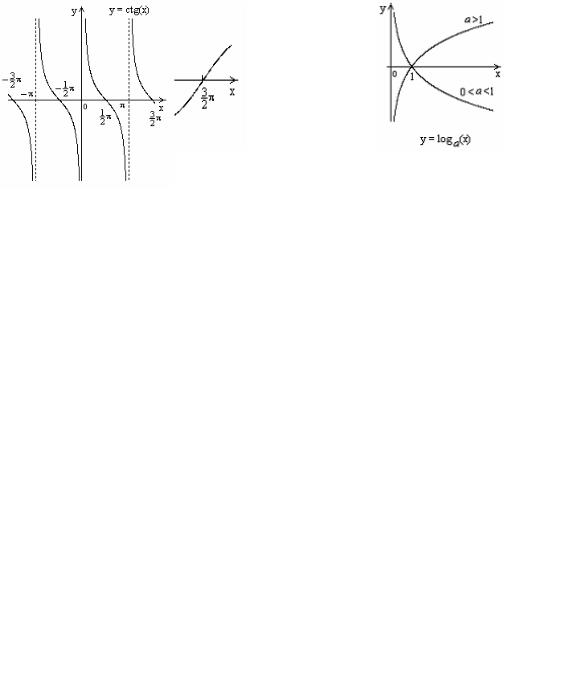
3. Тригонометрические функции

3.1. y = sinx		3.2. y = cosx

3.3. y = tg x, x ≠	π	+ nπ	3.4. y = ctgx, x ≠ kπ .
	2

Функции. Предел функции

117

4. Обратные тригонометрические функции

4.1. y = arcsin x, | x |≤1. arcsin(−x) = −arcsin x .

4.2. y = arccos x, | x |≤1. arccos(−x) =π −arccos x .



	4.3. y = arctg x ,		4.4. y = arcctg x .
arctg(−x) = −arctg x .		arcctg(−x) =π −arcctg x .

arcsin x + arccos x =			π		, arctg x + arcctg x = π , arctg x =			π		−arctg		1 .
			2			2		2				x
		5. Гиперболические функции
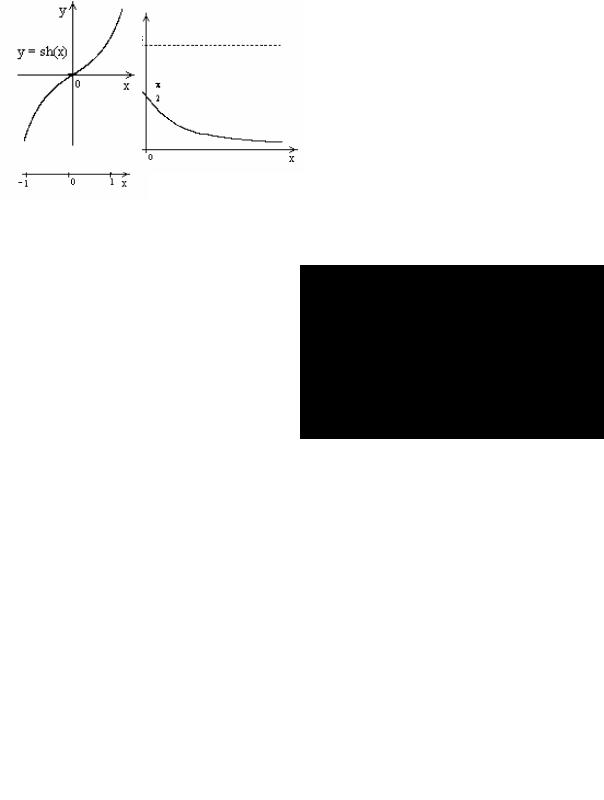
5.1. Гиперболический синус						5.2. Гиперболический косинус
	y = sh x =	ex −e−x					y = ch x =		ex + e−x
				.							.
		2		.						2	.
		2								2

118	Лекции 10 – 11

5.3. Гиперболический тангенс

y = th x =	ex −e−x	=	sh x	.
y = th x =	ex + e−x	=	ch x	.
	ex + e−x		ch x

ch2 x −sh2 x =1, th x cth x =1 , sh(x + y) = sh xch y +sh y ch x ,

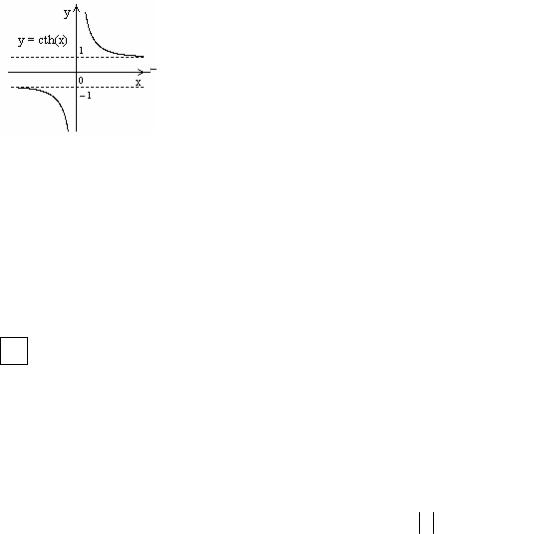
5.4. Гиперболический котангенс

y = cth x =	ex + e−x	=	ch x	.
y = cth x =	ex −e−x	=	sh x	.
	ex −e−x		sh x

ch(x + y) = ch xch y +sh xsh y .

10.5. Элементарные и неэлементарные функции

ОФункции, получающиеся из основных элементарных функций и констант с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций суперпозиции, называются

элементарными функциями.

(Список основных элементарных функций, изучаемых в рамках школьного курса математики, пополнен гиперболическими функциями – они широко встречаются в различных приложениях и тесно связаны с обыч-

ными тригонометрическими функциями.)

Рассмотренные выше функции y = sgn x , y = x , y =[x], функция Ди-

рихле относятся к неэлементарным.

11.1. Предел функции в точке

	11.1.1. Число A называется пределом функции y = f					(x)	в точке a , ес-
О
	ли	для	любой	последовательности	{xn}		такой,			что

	xn D( f ),		xn ≠ a, lim xn	= a , выполняется равенство		lim f (x		n	)= A , ко-
			n→∞			n→∞
	торое обозначают: lim f (x)= A .

x→a

Определение 11.1.1 сформулировано «на языке последовательностей»

(иначе определение предела по Гейне).

Функции. Предел функции		119
	Пример:
	1) y = x; xn → a	y(xn )= xn → a lim x = a.
	n→∞	x→a

2) y = y (x)− функция Дирихле, x → a, y →? рациональные−{xn } → a {y (xn )} →1,

иррациональные−{xn }→ a {y (xn )}→ 0.

Функция Дирихле не имеет предела при x → a , где a - любое.

О11.1.2. Число A называется пределом функции y = f (x) в точке a , ес-

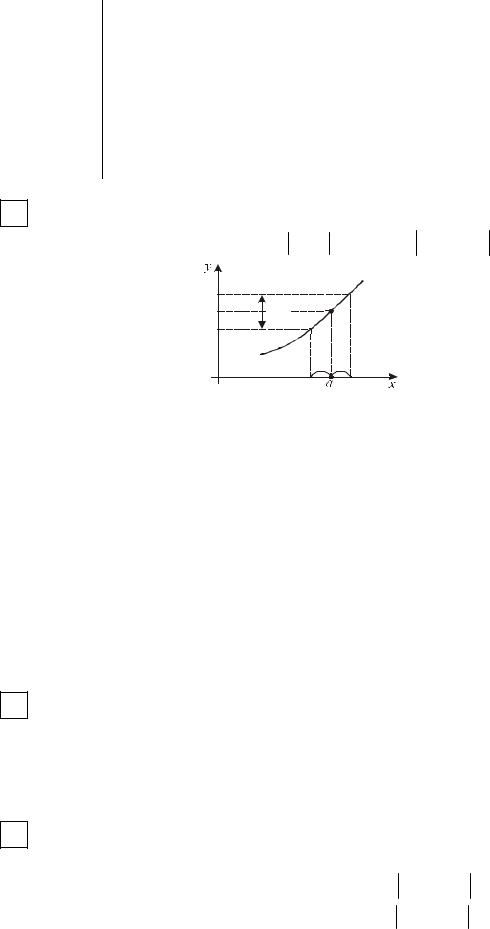
ли ε > 0 δ (ε ) > 0 : x : 0 < x − a < δ (ε ) f (x)− A < ε .

A + e
A	2ε
A - e
	δ	δ
0	a −δ	a +δ

Таким образом, для любой ε - окрестности точки А можно найти δ - окрестность точки a , такую, что все значения функции для x из δ - окрестности точки a попадут в ε - окрестность точки А.

Смысл этого утверждения заключается в том, что чем ближе точка x

расположена к точке a , тем ближе значение f (x) к числу A .

Определение 11.1.2 сформулировано «на языке эпсилон-дельта» (иначе оп-

ределение предела по Коши).

11.2. Предел функции в бесконечности

Если ООФ не ограничена сверху (снизу), то можно поставить вопрос о поведении функции при x →+∞ ( x → −∞).

О 11.2.1. Число A называется пределом			f (x) при x → +∞ ( x → −∞), ес-
		{xn}: xn → −∞
ли {xn}: xn → +∞ f {xn} → A		{xn}: xn → −∞		f {xn}→ A .
n→∞	n→∞		n→∞	n→∞

Определение 11.2.1 сформулировано «на языке последовательностей».

О11.2.2. Число A называется пределом f (x) при x → +∞ ( x → −∞),

если

ε > 0 M (ε ): x : x ≥ M f (x)− A < ε

( ε > 0 M (ε ): x : x ≤ M f (x)− A < ε ).

120	Лекции 10 – 11

Определение 11.2.2 сформулировано «на языке эпсилон-дельта».

ТОпределение 11.1.1 определение 11.1.2, определение 11.2.1 определение 11.2.2, т.е. определения Гейне и Коши эквивалентны.

Покажем, как пользоваться обеими разновидностями определений для доказательства существования и отсутствия предела. Для доказательства существования предела обычно удобнее определение Коши, для доказательства отсутствия предела – определение Гейне.

Пример:

1) y = x2 , x →1. Доказать, что lim x2 =1.

x→1

Доказательство:

ε > 0

x2 −1

< ε,

(x −1)(x +1)

< ε

x −1

x +1

Так как в предельном переходе рассматриваемая область значений x на-

ходится вблизи точки a =1 , можно считать,

что 0 < x < 2 ,

x +1

= x +1 ,

1 < x +1 < 3 ,

<1 , тогда

x −1

< ε , т.е. можно взять δ (ε )=ε . Что-

x +1

f (x)

при x → a , следует для любо-

бы доказать существование предела

го ε найти формулу для построения δ (ε ).

y =

x +1

, x →∞.

Доказать, что lim

x +1

=1 .

x→∞

Доказательство:

x +1

ε > 0

−1

< ε

, т.е. M (ε )=

y = sin

x → 0 . Доказать, что lim sin

не существует.

x→0

Доказательство:

Рассмотрим две последовательности

lim xn

= 0 ,

f (xn )= sin (nπ )= 0 ,

lim f (xn )= 0 ;

πn

n→∞

′

2nπ

′

= 0 ,

=1 ,

π + 4πn

lim xn

f (xn )= sin

lim f (xn )=1.

n→∞

Поскольку для различных последовательностей значений аргумента, сходящихся к нулю, соответствующие последовательности значений

функции сходятся к различным пределам, lim sin 1 не существует.

x→0 x

Функции. Предел функции

121

11.3. Односторонние пределы

О	11.3.1. Число A называется правым пределом функции			y = f (x)		в
	точке a , если {xn} → a , (xn > a) { f (xn )}→ A . Эквивалентное опре-
	деление: число A называется правым пределом функции y = f (x)					в
	точке a ,	если ε > 0 δ (ε ) > 0 : 0 < x − a <δ (ε )	f (x)− A		< ε .

	Обозначение правого предела: lim f (x ) = A .
		x → a +0
О	11.3.2. Число A называется левым пределом функции y = f (x) в точке
	a , если	{xn }→ a : (xn < a) {f (xn )}→ A, или если		ε > 0 ,		то

δ (ε )> 0 : 0 < a − x <δ (ε )		f (x)− A	< ε .
δ (ε )> 0 : 0 < a − x <δ (ε )		f (x)− A	< ε .
Обозначение левого предела:		lim f	(x ) = A .
		x → a − 0
Пример:
Пример:

	y = Sgn x , lim Sgn x =1,	lim Sgn x = −1.
	x→+0	x→−0

ТФункция y = f (x) имеет предел в точке a , если правый и левый преде-

лы в точке a существуют и равны: lim	f (x) = lim	f (x) = lim f (x) = A .
x→a+0	x→a−0	x→a

Доказательство:

Из определения 11.3.1 ε > 0 δ1 (ε ): 0 < x − a <δ1 (ε ) f (x)− A < ε .

Из

определения

11.3.2

для

того

же

δ2 (ε ): 0 < a − x < δ2 (ε )

f (x)− A

< ε .

Возьмем

δ (ε )= min{δ1,

δ2},

тогда

можно

сказать,

что

ε > 0 δ (ε ):

x − a

<δ (ε ), то есть lim f (x)= A .

x→a

11.4.Бесконечно малые и бесконечно большие функции

иих свойства

	Функция α (x) называется бесконечно малой	в точке	a , если
О
	limα (x) = 0 .

!	x→a		x → +∞
	Аналогично определяется функция, бесконечно	малая при

122	Лекции 10 – 11

( x → −∞).

Функции. Предел функции

123

Свойства бесконечно малых функций:

))

x→a

(

)

x→a

(

)

x→a (

(

)

+ β

(

= 0 .

Если limα

= lim β

= 0 , то lim

Доказательство:

Из условия следует, что для любой последовательности xn → a соответствующие последовательности α(xn )→ 0 и β (xn )→ 0 .

Покажем, что α(xn )+ β (xn )→ 0 . Для этого фиксируем произвольное ε :

N1 (ε ): n > N1 α(xn ) < ε2 и N2 (ε ): n > N2 β (xn ) < ε2 .

Возьмем N = max{N1, N2},

тогда для n > N α (xn )+ β (xn ) ≤ α (xn ) + β (xn ) < ε .

!Свойство может быть расширено: сумма конечного количества бесконечно малых функций есть бесконечно малая функция.

ТПроизведение бесконечно малой функции на ограниченную функцию есть функция бесконечно малая.

лая.

Например,			2	sin	1	= 0.	x	2	- бесконечно малая функция в точке
Например,		lim x		sin	x	= 0.	x		- бесконечно малая функция в точке
		x→0			x
x = 0 ; sin	1	- ограниченная функция.
	x

Произведение бесконечно малых функций есть функция бесконечно ма-

Если lim f (x)= A ≠ 0, limα (x)= 0 , то lim			α (x)	= 0.
Если lim f (x)= A ≠ 0, limα (x)= 0 , то lim			f (x)	= 0.
x→a	x→a	x→a	f (x)
Функция	f (x) называется	бесконечно	большой в точке a , если

M δ (M )> 0 : x : 0 < x −a <δ f (x) > M . Записывается это как

lim f (x)= ∞. Если же функция при x → a не только возрастает по абсо-

x→a

лютной величине, но и сохраняет определенный знак, это обозначают:

lim f (x)= +∞ M δ (M )> 0 : x : 0 < x − a <δ f (x)> M ;

x→a

lim f (x)= −∞ M δ (M )> 0 : x : 0 < x − a <δ f (x)< M .

x→a

!1). Аналогично определяются функции, бесконечно большие при

x → +∞ ( x → −∞ ).

2). Функция, бесконечно большая при x → a , является неограниченной в окрестности точки a , но обратное утверждение неверно: не всякая не-

ограниченная функция является бесконечно большой. Так, f1 (x)= 1x -

124					Лекции 10 – 11
				1
			sin
бесконечно большая при x →0 , а f2 (x)=				x	- является неограни-
бесконечно большая при x →0 , а f2 (x)=				x	- является неограни-
				x
ченной при x → 0 , но бесконечно большой не является.
В первом случае для любого числа	M можно указать окрестность
точки x = 0 , в каждой точке которой		f (x)		> M ; во втором случае для
точки x = 0 , в каждой точке которой		f (x)		> M ; во втором случае для

любого числа M в каждой окрестности точки x = 0 можно указать точку, в которой f (x) > M , но в этой же окрестности найдутся точки,

не удовлетворяющие этому условию, для которых, например, f (x)= 0 .

Связь между функциями бесконечно большими и бесконечно малыми при x → a подтверждается следующей теоремой.

ТЕсли α (x) - бесконечно малая функция при x → a и α(x)≠ 0 при x ≠ a ,

то α(1x) - бесконечно большая функция при x → a . Если α(x) - беско-

нечно большая, то α(x) - бесконечно малая.

Свойства бесконечно больших функций

1˚. Произведение бесконечно большой функции на ограниченную функцию, не равную нулю, есть функция бесконечно большая.

2˚. Произведение бесконечно больших функций есть функция бесконечно большая.

3˚. Сумма бесконечно больших функций может не быть бесконечно боль-

шой функцией:
f (x)= x , g (x)=1 − x ,	f (x)+ g (x)=1.	f (x) и g (x) - бесконечно боль-
шие при x → ∞ функции, но f (x)+ g (x)		таковой не является;
f (x)= x , g (x)=1 − x2 , f (x)+ g (x)=1 + x − x2 .
Все функции, f (x),	g (x) и f (x)+ g (x) - бесконечно большие при

x → ∞.

11.5.Таблица определений предела

Втаблице приведены все встречавшиеся в лекции определения пределов. Для краткости приведены только определения Коши.

Функции. Предел функции

125

Понятие

Обозначение

Определение

Предел функции

lim f

(

)

= A

(

)

0 : x : 0

f (x)

ε >

−

< δ

−

< ε

f в точке x = a

x→a

«Обращение

lim f (x)= +∞

(M )

−

<δ

f (x)

функции f

x→a

0 : x : 0

lim f

(x)= −∞

(M )

0 :

x : 0

f (x)

в бесконеч-

−

<δ

ность» в точке

x→a

x = a

lim f

(

)

= ∞

M δ (M )> 0 : x : 0 <

x − a

< δ

f (x)

> M

x→a

Предел функции

lim

(

)

= A

ε > 0

M (ε ): x : x ≥ M

f (x)− A

< ε

f при x → +∞,

x→+∞

соответственно

x→−∞

(

)

= A

ε > 0

M (ε ): x : x ≤ M

f (x)− A

< ε

x → −∞

lim

«Обращение

lim

f (x)= +∞

x0 (M ): x :

x ≥ x0 f (x)> M

функции f

x→+∞

в бесконеч-

lim

f (x)= −∞

x0 (M ): x :

x ≥ x0 f (x)< M

ность» при

x→+∞

lim

(

)

= +∞

)

: x :

x ≤ x f

(

)

> M

x → +∞,

x→−∞

0 (

соответственно

lim

f (x)= −∞

x0 (M ): x :

x ≤ x0 f (x)< M

x → −∞

x→−∞

lim

f (x)= ∞

x0 (M ): x : x ≥ x0

f (x)

> M

x→+∞

lim

f (x)= ∞

x0 (M ): x : x ≤ x0

f (x)

> M

x→−∞

Пределы справа

lim

(

)

= A

ε > 0

δ (ε )> 0 : x : 0 < x − a < δ

f (x)− A

< ε

и слева

x→a+0

x→a−0

(

)

= A

ε > 0 δ (ε )> 0 : x : 0 < a − x < δ f (x)− A < ε

lim

«Обращение

lim

f (x)= +∞

δ (M )> 0 : x : 0 < x − a < δ f (x)> M

функции f

x→a+0

в бесконеч-

lim

(

)

= +∞

(

)

> 0 : x : 0 < a − x <δ f

(

)

> M

x→a−0

ность» справа и

lim

f (x)= −∞

δ (M )> 0 : x : 0 < x −a <δ f (x)< M

слева

x→a+0

в точке x = a

lim

f (x)= −∞

δ (M )> 0 : x : 0 < a − x < δ f (x)< M

x→a−0

x→a+0

(

)

= ∞

M δ (M )> 0 : x : 0 < x − a < δ f (x) > M

lim

x→a−0

(

)

= ∞

M δ (M )> 0 : x : 0 < a − x < δ f (x) > M

lim

В результате изучения материала, изложенного в этих лекциях, студент должен владеть следующими понятиями:

функция, график функции, способы задания функции;

предел функции в точке и в бесконечности, односторонние пределы;

бесконечно малые и бесконечно большие функции, их свойства.

Лекции 12-13 ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ

В лекциях 12–13 доказаны основные теоремы, на которые опираются конкретные приемы вычисления пределов функций. Рассмотрены первый и второй замечательные пределы, позволяющие вычислять пределы неопределенных выражений, приведена классификация бесконечно малых величин, показана важность эквивалентных бесконечно малых для вычисления пределов функций. Рассмотрено понятие непрерывности, излагаются определения и теоремы, разъясняющие это понятие.

12.1.Свойства функций, имеющих предел

12.2.Замечательные пределы

12.2.1.Первый замечательный предел

12.2.2.Второй замечательный предел

12.3.Сравнение бесконечно малых функций

13.1.Непрерывность функции

13.1.1.Непрерывность функции в точке

13.1.2.Непрерывность функции на множестве

13.1.3.Непрерывность основных элементарных функций

13.1.4.Свойства непрерывных функций

13.1.5.Непрерывность обратной функции

13.1.6.Непрерывность сложной функции

13.1.7.Свойства функций, непрерывных на отрезке

13.2.Точки разрыва и их классификация

12.1.Свойства функций, имеющих предел

Для рассмотрения свойств функций, имеющих предел, будет полезна следующая теорема о связи бесконечно малой функции и функции, имеющей предел. Теоремы этого параграфа сформулированы для пределов в точке x0 ,

но все они справедливы и для пределов при x → ±∞.

Т	Если lim f (x) = A и A < ∞, то f (x) = A +α(x), где limα (x) = 0.
	x→x0		x→x0
	x→x0		x→x0
	Доказательство:
	Если lim f (x) = A, то, по определению Коши, при произвольном ε > 0
	x→x0	f (x)− A		f (x)− A	=α (x).
	выполняется неравенство		< ε . Обозначим
	выполняется неравенство		< ε . Обозначим

Тогда для любого ε > 0 выполняется α (x) < ε . Но это и означает, что α(x) – бесконечно малая при x → x0 .

126	Лекции 12 – 13

!Справедливо и обратное утверждение: если функция f (x) представима

	в виде		f (x) = A +α(x), где limα(x) = 0 , то существует lim f (x) = A.
	в виде
									x→x0	x→x0
Пусть функции y = f (x)							и y = ϕ (x)			имеют одну область определения D .

Т	Если lim f ( x) = A и limϕ(x) = B , то
		x→x0					x→x0
		x→x0					x→x0
1)		lim ( f (x) +ϕ (x)) = lim							f (x) + lim ϕ (x);
		x→x0						x→x0		x→x0
2)		lim ( f (x) ϕ (x))= lim							f (x) lim ϕ (x);
		x→x0					x→x0			x→x0
3)		lim (k f (x))= k lim f (x);
		x→x0					x→x0
				f (x)		lim f (x)
4)		lim		f (x)	=	x→x0		, где ϕ (x) ≠α (x) .
4)		lim	ϕ (x)		=	lim ϕ	(x)	, где ϕ (x) ≠α (x) .
		x→x0	ϕ (x)			lim ϕ	(x)
						x→x0
	Из теоремы о связи функции, предела и бесконечно малой:
lim f (x) = A f (x) = A +α(x),										где limα(x) = 0;
x→x0										x→x0
lim ϕ (x) = B ϕ (x) = B + β(x),										где lim β(x) = 0
x→x0										x→x0

Докажем свойство 1:

f(x) + ϕ (x) = (A + α (x))+ (B + β (x))=

=(A + B)+ (α (x)+ β (x))= (A + B)+γ (x),

где γ (x)=α(x)+ β (x).

Применяя теорему о связи вновь и учитывая, что

	lim γ (x) = lim (α(x) + β(x))= 0,
	x→x0	x→x0
получаем	( f (x) +ϕ (x))= A + B = lim f (x) + limϕ (x).
lim	( f (x) +ϕ (x))= A + B = lim f (x) + limϕ (x).
x→x0		x→x0	x→x0

!Свойства 1, 2, 4, в которых фигурируют три различных предела, можно читать в двух направлениях: если два любых предела существуют, то существует и третий и соотношение выполняется.

Замечательные пределы. Непрерывность функции

127

Пример:

Вычислить предел lim

+ 5

− 3

x→2

Значение

функции

(x) =

определено

точке

x = 2 ,

−

f (2) =

+ 5

= 9 , поэтому

lim

x2 + 5

− 3

x2 − 3

x→2

Если функция f (x)

определена в точке x0 , то

lim f (x) = f

lim x

)

= f (x0 ).

x→x0

(x→x0

Пример:

Вычислить предел lim

+ x

− 3x2

x→∞ x3

Как и для последовательностей, применим метод деления числителя и

знаменателя на наивысшую степень x , т.е. на x3 :

x3 + x

∞

1+1 x2

1+ 0

lim

= lim

=1.

−3x

−3 x +1 x

−0 +

x→∞ x

∞

x→∞ 1

Пример:

Вычислить предел lim

9 +5x + 4x2

−3

x→0

Непосредственно подставляя число x0

= 0 в функцию, получаем неопре-

деленность (0/0). Учтем формулу (a −b)(a + b) = a2

−b2

и умножим чис-

литель и знаменатель на выражение (

9 +5x + 4x2 +3):

9 +5x +4x2

−3

( 9 +5x + 4x2 )2 −(3)2

lim

= lim

9 +5x +4x2 +3)

x→0

x→0 x (

= lim

+5x +4x2 −9

= lim

5 +

5 +0

x→0 x ( 9 +5x +4x2 +3)

x→0

9 +5x +4x2 +3

9 +0 +0 +

5 .

128

Лекции 12 – 13

Пример:

Вычислить предел: xlim→+∞ (

x2 +1 − x).

В данном примере имеет место неопределенность типа (∞ - ∞); наличие

иррациональности не допускает прямого сокращения, поэтому применя-

ется следующий прием:

f (x)− g (x)=

(f (x)− g (x))( f (x)+ g (x))

f 2 (x)− g2 (x)

f (x)+ g (x)

lim (

x2 +1 − x) =(∞−∞) = lim

( x2 +1)2 − (x)2

x2 +1 + x

x→+∞

x2 +1− x2

= lim

= 0

x→+∞

x2 +1 + x

x→+∞ x2

+1 + x

Если функции

y = f (x)

и y =ϕ(x)

имеют одну область определения D

и x D f (x)≤ϕ(x),

то lim f (x) ≤ limϕ(x). Иначе говоря, знак нера-

x→x0

венства сохраняется при предельном переходе. Заметим, что из строгого

неравенства f

(x)<ϕ(x) по-прежнему следует lim f (x) ≤ limϕ(x) : пусть

x→x0

f (x)= x4 , ϕ (x)= x2 , при

f (x)<ϕ(x), но lim f (x) = limϕ(x) = 0 .

x→0

Теорема о пределе промежуточной функции.

Если 1) x D f (x)≤ϕ(x)≤ g (x)

, 2) lim f (x) = lim g(x) = A ,

x→x0

то limϕ(x) = A.

x→x0

12.2.Замечательные пределы. Первый замечательный предел. Второй замечательный предел

Втеории пределов большую роль играют два предела, которые, в силу их важности, получили названия замечательных пределов.

12.2.1. Первый замечательный предел

		y = sin x	при x → 0 имеет предел, равный 1: lim sin x		=1.
Т	Функция
		x	x→0	x

Замечательные пределы. Непрерывность функции										129
Доказательство:
Рассмотрим единичную окружность.
Пусть COB = x , 0 < x < π		, OC = OB = r =1 ,
	2
AC = sin x ,	OA = cos x , BD = tg x . Сравнивая
площади треугольника OAC , сектора OBC
и треугольника OBD , получаем
S OAC < SOBC < S OBD ,
1 sin x cos x < 1 x < 1			sin x .
2	2	2	cos x
Разделим двойное неравенство на				sin x (> 0):	cos x <	x	<	1		. Нера-
Разделим двойное неравенство на				sin x (> 0):	cos x <	sin x	<		cos x	. Нера-
				2		sin x			cos x
венство	справедливо		и	для	x < 0 ,			так		как
cos(−x) = cos x, sin(−x) = sin(x) . Перейдем к пределу при							x → 0 : cos(x)
	−x	x
- функция непрерывная, cos x →cos(0) =1. Применяя теорему о пределе
промежуточной функции, получаем:
	1 ≤ lim sin x ≤1, то есть lim sin x =1.
	x→0	x		x→0	x

!В первом замечательном пределе имеет место неопределенность 0 .

Пример:

Вычислить предел: lim sin 2x .

x→0 x

Если x → 0, то и 2x → 0 и тогда

sin 2x

2 sin 2x

sin 2x

lim

= lim

= 2 lim

= 2

= 2.

2 x

x→0

Пример:

Вычислить предел: lim tgx .

x→0

tg x

sin x

lim

= lim

lim

= 1

= 1.

cos x

cos0

x→0

cos x

x→0

130									Лекции 12 – 13
	12.2.2. Второй замечательный предел
		Функция		+	1 x
	Т				1 x
	Т		y(x)= 1			при x → ∞ имеет предел, равный числу e :
					x		+	1	x
					x

						lim 1		x	= e .
						x→∞		x

Доказательство:

При рассмотрении предела монотонной последовательности было полу-

чено соотношение:

1 n

= e .

lim 1

x →+∞.

n→∞

Пусть

Любое

удовлетворяет

двойному

неравенству

n ≤ x < n +1 ,

где

n =[x]

целая

часть

x .

Тогда

< 1

≤ 1 ,

n +1

1 n

n+1

<1+

≤1

x → +∞

1 +

< 1 +

≤ 1

. При

n +1

n →+∞.

Рассмотрим раздельно пределы левой и правой части двойного неравенства:

n+1

lim 1

n→∞

n +1

= e

lim 1

n→∞

lim 1 +

n→∞

n+1

= e 1 = e .

lim 1

= lim 1 +

lim 1 +

n→∞

Применяя теорему о пределе промежуточной функции, получаем, что

	+	1 x		+	1 x
e ≤ lim 1	+		≤ e , откуда lim 1	+		= e.
x→+∞		x	x→+∞		x

Пусть x → −∞. Сделаем замену переменной: t = −(x +1),

x = −(t +1);

из x → −∞ следует t → +∞.

−t−1

t +1 t+1

lim 1

= lim 1−

= lim

x→−∞

t→+∞

t +1

t→+∞ t

t→+∞

1 t+1

1 t

= e 1

= e

= lim 1 +

= lim 1

= lim 1 +

lim 1

t→+∞

Замечательные пределы. Непрерывность функции

131

С lim(1+t)1/ t = e

t→0

(заменим переменную: t =	1	; lim(1+t)1/ t = lim(1+1 x)x = e ).
	x	t→0	x→∞

Пример:

Вычислить предел: lim (1 +1 x)7 x .

x →∞

(1+1 x)

7 x

∞

+1 x)

x 7

(1+1 x)

x 7 7

lim

= lim

lim

= e .

x→∞

ОФункция y = ( f (x))ϕ(x) ( f (x)> 0 ) называется степенно-показательной функцией или сложно-показательной функцией.

ТПредел степенно-показательной функции y = ( f (x))ϕ(x) при x → x0 вычисляется по формуле:

			lim ϕ ( x)
lim ( f (x))ϕ ( x) = lim f (x) x→x0				.
0		0
x→x	x→x

Применим основное логарифмическое тождество, считая lim f (x) = A, lim ϕ (x) = B.

		x→x0			x→x0
			ϕ ( x )				lim ϕ ( x) ln f ( x)	=
lim ( f (x))ϕ ( x) = lim eln( f ( x))					= lim eϕ ( x) ln f ( x) = ex→x0			=
x→x0		x→x0			x→x0
lim ϕ ( x) lim ln f ( x)							lim ϕ ( x)
lim ϕ ( x) lim ln f ( x)			= eB ln A	= eln AB = AB = lim			f (x) x→x0 .
= ex→x0	x→x0		= eB ln A	= eln AB = AB = lim			f (x) x→x0 .
					x→x
						0

!Во втором замечательном пределе имеет место неопределенность 1∞ .

Пример:

x +1 2 x−1

Вычислить предел lim

x→∞ x − 2

Вычислим

предел

lim

x +1

= lim

1 +1 x

1 + 0

предел

1 − 0

x →∞ x − 2

x→∞ 1 − 2 x

(2x −1) = ∞. Таким образом, функция

x +1

2 x −1

lim

y =

порождает не-

x →∞

x − 2

определенность [1∞].

x +

x +1

− x +

−1 =1+

=1+

x −

−2

((x −2) 3)

x −2

132

Лекции 12 – 13

x +1

2 x−1

∞

2 x−1

lim

= (1 )

= lim

x→∞ x − 2

x→∞

((x − 2) 3)

x−2

(2 x−1)

x−2

3(2 x−1)

lim

= lim 1

= ex→∞

x−2

= e6 ,

x→∞

((x

− 2) 3)

поскольку lim

6x −3

= 6.

x→∞

x −2

12.3. Сравнение бесконечно малых функций

Пусть функции α1(x) и α2(x) являются бесконечно малыми при x → x0.

Если lim α1(x) = A, то возможно несколько ситуаций:

x→x0 α2 (x)

1)если A < ∞, то α1(x) и α2(x) называются бесконечно малыми одного порядка;

2)если A = 1, то α1(x) и α2(x) называются эквивалентными. Обозначение:

α1(x) α2(x) lim α1(x) =1;

x→x0 α2 (x)

3) если A = 0, то функция α1(x) называется бесконечно малой высшего порядка по сравнению с α2(x).

Введем символ α1(x) = о (α2(x)) lim α1(x) = 0.

x→x0 α2 (x)

Т Если α1(x), α2(x), α3(x) являются бесконечно малыми при x → x0 и при

этом α1(x) α2(x), α2(x) α3(x), то lim

α1(x)

= lim

α1(x) .

x→x0

α2 (x)

x→x0

α3 (x)

В самом деле, α3(x) α2(x) lim

α3 (x) =1.

x→x0

α2 (x)

Тогда

lim

α1(x)

= lim

α1(x) α3 (x)

= lim

α1(x)

lim

α3 (x) = lim

α1(x)

1 =

x→x0

α2 (x)

x→x0

α3 (x) α2 (x)

x→x0

α3 (x)

x→x0

α2 (x)

x→x0

α3 (x)

= lim

α1(x) .

x→x0

α3 (x)

Замечательные пределы. Непрерывность функции					133
Аналогично: если α1(x) α2(x) при x → x0, то
1)	lim ( f (x) α1(x)) = lim ( f (x) α2 (x));
	x→x0			x→x0
2)	lim	α1(x)	= lim	α2 (x)	;
	x→x0	f (x)	x→x0	f (x)
3)	lim f (α1(x))= lim f (α2 (x)).
	x→x0			x→x0

ТЕсли x → 0, то выполняются следующие эквивалентности:

1) sin x x	5) arcsin x x		9) 1−cos x		x2
1) sin x x	5) arcsin x x		9) 1−cos x		2
					2
2) tg x x	6) arctg x x		10)	sh x x
3) ex – 1 x	7) ln(1 + x) x		11)	1± x −1 ±		x
3) ex – 1 x	7) ln(1 + x) x		11)	1± x −1 ±		2
4) ax −1 x ln a	8) loga (1+ x)	x	12)	(1 + x)α −1 αx
4) ax −1 x ln a	8) loga (1+ x)	ln a	12)	(1 + x)α −1 αx
		ln a

!Указанные эквивалентности являются следствиями соответствующих предельных соотношений:

sin x →1,					ax −1	= →ln a			,
x	x→0					= →ln a			,
					x			x→0
					x
tg x →1,					(1+ x)a −1			= →a ,
x	x→0				x			= →a ,
x					x			x→0
								x→0
loga (1+ x) = →			1	,	1+ x −1		= →		1	.
					1+ x −1				1

	x	x→0	ln a		x				2
	x		ln a		x			x→0	2
								x→0

Пример:

Вычислить предел lim (1 + sin x)1 x .
	x →0
При x → 0 применим sinx x.
lim (1 + sin x)1 x = lim (1 + x)1 x = e.
x →0	x →0

Пример:

Вычислить lim ln(1 + sin x) .
x→0	sin 4x

При x → 0 применим эквивалентность sinx x, sin4x 4x.

134

Лекции 12 – 13

lim

ln(1 + sin x)

= lim

ln(1 + x)

lim

ln(1 + x)

1 =

x→0

sin 4x

x→0

4 x→0

Пример:

Вычислить lim

1 + cosπ x

x →1

tg2π x

Заменим t = x - 1. Получаем t → 0 и x = t + 1, тогда cos πx = cosπ(t + 1) =

= cos (πt + π) = -cosπt, tg2πx = tg2π(t + 1) = tg2(πt + π) = tg2πt.

2 sin2 πt

πt 2

+ cosπ x

− cosπt

2 2 =

lim

= lim

= 2 lim

x→1

π x

t →0

tg πt

t →0

tg πt

t →0

(πt)

= 2 lim

π 2t2

2 lim

π 2t2

t →0

4 2

13.1. Непрерывность функции

13.1.1. Непрерывность функции в точке

О	Пусть функция	y = f (x)	определена на множестве D и пусть точка
	x0 D . Функция	y = f (x)	называется непрерывной в точке x0 , если
	x0 D . Функция	y = f (x)	называется непрерывной в точке x0 , если
	функция определена в точке x0 , существует предел lim f (x) и при этом
				x→x0
	lim f (x) = f (x0 ). (Иначе: 1) f (x0 ) , 2) lim f (x) , 3) lim f (x) = f (x0 ) ).
	x→x0		x→x0	x→x0

!1). При нарушении любого из трех условий функция называется разрывной в точке x0 .

2). Поскольку lim x = x0 , поэтому первое определение непрерывности
x→x0		)
может быть записано в виде lim f (x) = f	lim(x)		, то есть операция вы-
x→x0	(x→x0

числения непрерывной в точке x0 функции y = f (x) и операция вычисления предела перестановочны.

Пример:

1)	f (x) = x , x	lim f (x) = lim x = x = f (x ) .
	0	x→x	x→x	0	0
		0	0
f (x) = x - непрерывна в любой точке					x0 по опре-

делению.
2) f (x) =		2	, x < 0,		1
2) f (x) =	x		, x < 0,		1
	1, x ≥ 0.
f (x) непрерывна в любой точкеx0				≠ 0 ,	0
					0

Замечательные пределы. Непрерывность функции

135

f (x) разрывна в точке 0 (нарушено второе условие определения).

Рассмотрим точку x0 D функции y = f (x) и точку x ≠ x0 .

Величина ∆x = x − x0 называется приращением аргумента, x = x0 +∆x .

Величина ∆ y = f (x0 + ∆x)− f (x0 ) называется приращением функции, соответствующим данному приращению аргумента ∆x .

О Функция y = f (x) называется непрерывной в точке x0 , если функция

определена в точке x0 и при этом lim ∆y = 0.

∆x→0

Вариант формулировки: функция непрерывна в точке, если беско-

нечно малым приращениям аргумента соответствуют бесконечно малые приращения функции.

Пример:

Показать, что первое и второе определения непрерывности равносильны. Используя арифметические свойства предела, получаем

			lim ∆y = 0, lim		[ f (x0 + ∆x) − f (x0 )]= 0,
			∆x→0	∆x→0
			lim f (x0	+ ∆x) − lim		f (x0 ) = 0,		lim	f (x0 + ∆x) − f (x0 ) = 0.
			∆x→0		∆x→0			∆x→0
	По определению приращения ∆x = x − x0 , поэтому
					lim	f (x0	+ ∆x) = lim f (x),
					∆x→0			x→	х0
	и тем самым lim			f (x) − f (x0 ) = 0			или	lim	f (x) = f (x0 ).
			x→x0					x→x0
	Функция	y = f (x) называется непрерывной в точке x0 , если функция
О	Функция	y = f (x) называется непрерывной в точке x0 , если функция
	определена в		точке	x0 ,	существуют				односторонние пределы
	определена в		точке	x0 ,	существуют				односторонние пределы
	lim f (x),	lim	f (x) и при этом			lim f (x) = lim f (x) = f (x0 ) .
	x→x0 −0	x→x0 +0				x→x0 −0		x→x0 +0

!Все три определения непрерывности равносильны. Используется также понятие односторонней непрерывности.

ОФункция y = f (x) называется непрерывной в точке x0 слева, если функция определена в точке x0 и существует односторонний предел

lim f (x) и при этом	lim f (x) = f (x0 ) .
x→x0 −0	x→x0 −0

ОФункция y = f (x) называется непрерывной в точке x0 справа, если функция определена в точке x0 и существует односторонний предел

lim f (x) и при этом	lim	f (x) = f (x )	.
lim f (x) и при этом	x→x +0	0	.
x→x +0	0
0

136	Лекции 12 – 13

!Используя понятие односторонней непрерывности, можно сказать, что

функция непрерывна в точке x0 , если она непрерывна в ней справа и слева.

13.1.2. Непрерывность функций на множестве

ОФункция, непрерывная в любой точке множества D , называется не-

прерывной на множестве D .

Для некоторых точек множества двусторонние пределы могут не суще-

ствовать, например, если в качестве множества D рассматривается отрезок [a,b]. В этом случае в крайних точках отрезка двусторонние пределы заменяются на односторонние.

ОФункция непрерывна на отрезке [a,b], если она непрерывна на интервале (a,b), непрерывна справа в точке a и непрерывна слева в точке b .

13.1.3. Непрерывность основных элементарных функций

Основными элементарными функциями обычно называют следующие: y = xα , ax , loga x , sin x , cos x , tg x , ctg x, arcsin x , arccos x , arctg x , arcctg x.

ТОсновные элементарные функции непрерывны в каждой точке x0 их области определения.

Пример:

!Непрерывность функции y = xn в произвольной точке x0 вещественной оси доказывается с использованием формулы бинома Ньютона.

Пример:

Показать, что функция f (x) = sin x		непрерывна в произвольной точке x0
вещественной оси.
Докажем, что:
1) lim sin x = 0 . {xn } → +0		(x > 0) .
x→+0
По лемме 0 < sin xn < xn	при n → ∞ , по теореме о переходе к пределу в
неравенствах lim sin xn	= 0 . lim sin x = 0 = sin(0) - непрерывность в
n→∞	x→0+

Замечательные пределы. Непрерывность функции

137

точке x = 0 справа. Пусть {xn} → −0 . Заменим x на (−x), (−x) > 0 .

Тогда выполняется условие: 0 < sin(−x) < (−x) , 0 < −sin x < (−x) .

Умножим

неравенство

на

(-1).

Тогда

0 > sin x > x .

Рассмотрим

(xn < 0) ,

xn < sin xn < 0

lim sin x = 0 = sin(0) - непрерывность в

точке x =0 слева.

x→0−

2) точки x = x0 ≠ 0 .

Покажем,

что lim sin x = sin x0 ,

то есть

lim(sin x − sin x0 ) = 0 .

x→x0

sin x −sin x

= 2 cos

x + x0

sin

x − x0

x + x0

lim (sin x −sin x0 ) = 2 lim (cos

x + x0

sin

x − x0

) = 0

(так как

cos

x→x0

величина ограниченная,

sin

x − x0

- бесконечно малая и →0 ) и все

произведение →0 .

Пример:

Вычислить предел: lim sin x.

x→π4

Функция y = sinx непрерывна в любой точке, поэтому

			π			2
lim sin x = sin lim x			π			2	.
			= sin		=
			= sin	4	=	2
x→π	x→π			4		2
4		4

13.1.4. Свойства непрерывных функций

ТЕсли функции y = f (x) и y =ϕ(x) определены на множестве D и непрерывны в точке x0 D , то функции

+ϕ ϕ )(x), k f (x),f (x) (x),f (x) f (x

ϕ(x)

непрерывны в точке x0 , причем частное требует условия ϕ(x0 )≠ 0 . Поскольку функции непрерывны в точке x0 , выполняется условие:

	lim f (x) = f (x0 ),		limϕ (x) =ϕ (x0 ).
	x→x0		x→x0
Используя арифметические свойства предела, получаем:
lim	( f (x) +ϕ (x))= lim f (x) + limϕ (x) = f (x0 ) +ϕ (x0 ),
x→x0		x→x0	x→x0
но это и означает, что функция		f (x)+ϕ(x) непрерывна в точке x0 .

138	Лекции 12 – 13

С1). Многочлен Pn(x) = anxn + … +a1x + a0 непрерывен в любой точке x0 вещественной оси.

2). Дробно-рациональная функция R(x) =	P (x)	=	a xn +... + a x + a			не-
	n		n	1	0
	Q (x)
			b xm +... + b x + b
	m		m	1	0

прерывна в любой точке x0 вещественной оси, где Qm(x0) ≠ 0.

ТЕсли функция y = f (x) непрерывна в точке x0 , то она ограничена в некоторой окрестности этой точки.

ТОб устойчивости знака непрерывных функций.

Если f (x)

- непрерывна

в точке

f (x0 ) ≠ 0 ,

то

такая δ -

окрестность

точки x0 , что

для всех

значений x из этой окрестности

f (x) ≠ 0 и имеет знак, совпадающий со знаком f (x0 ) .

Доказательство:

По условию, lim f (x) = f (x0 ) .

x→x0

Таким образом, ε > 0 δ :

x − x0

<δ

f (x) − f (x0 )

< ε ,

то есть, f (x0 ) −ε < f (x) < f (x0 ) +ε .

Если взять ε : ε <

f (x0 )

, то числа f (x0 ) −ε ,

f (x0 ) +ε

f (x0 ) должны

иметь одинаковый знак. Таким образом, для ε < f (x0 ) , f (x) из ε - окрестности имеет один знак с f (x0 ) .

13.1.5. Непрерывность обратной функции

ТЕсли:

1)y = f (x) - строго монотонная, непрерывная на [a,b],

2)α = f (a), β = f (b) , то x = f −1 ( y) - строго монотонная, непрерывная на [α, β].

Пример:

y = sin x , на	−	π	,	π	- строго монотонна и непре-
		2		2

рывна имеет строго монотонную и непрерывную обратную функцию x = arcsin y на [−1,1].

После переобозначения y = arcsin x .

13.1.6. Непрерывность сложной функции

ОФункции, полученные в результате суперпозиции двух или большего числа функций, называются сложными:

Замечательные пределы. Непрерывность функции				139
	Пусть: 1) x =ϕ(t) задана на {t} и имеет	множество	значений	{x};
О	Пусть: 1) x =ϕ(t) задана на {t} и имеет	множество	значений	{x};
	2) y = f (x) задана на {x}.
	2) y = f (x) задана на {x}.
	Тогда на {t} задана сложная функция	y = f (x) , где	x =ϕ(t)	или

y = F(t) = f [ϕ(t)], x - промежуточный аргумент, t - независимая переменная.

Пример:

y =sin x , x = t2 , y = sin t2 - сложная функция.

ТНепрерывность сложной функции.

Если: 1) x =ϕ(t) непрерывна в точке t = a ,

2)y = f (x) непрерывна в точке x = b =ϕ(a) ,

то y = f [ϕ(t)] непрерывна в точке t = a .

Доказательство:
Используя определение предела по Гейне, докажем, что
				lim f [ϕ(t)]= f [ϕ(a)]= f (b) .
{ n}			{	t→a
		→ a		n }
t			ϕ(t	) →ϕ(a) = b (доказано условие 1)),
xn =ϕ(tn ) , то есть {xn} →b , { f (xn )} → f (b) (доказано условие 2)),
но	f (xn ) = f [ϕ(tn )], то есть {tn} → a , {f [ϕ(tn )]}→ f [ϕ(a)] f [ϕ(t)] -

непрерывна в точке t = a , что и требовалось доказать.

!1). Если исходные функции непрерывны, то в результате их сложения,

вычитания, умножения, деления (если знаменатель ≠ 0 ), взятия обратной и сложной функций получаются непрерывные функции.

2).	Для непрерывной в точке x0 функции f (x) справедливо:
lim f (x) = f (x0 ) = f (lim x) .
x→x0	x→x0

Для непрерывных функций переходить к пределу можно под знаком функций:

а) б)

lim ex	2	lim x2	= e25 ,
lim ex		= ex→5	= e25 ,
x→5

lim ln(1 + sin x) = ln(lim(1 + sin x)) = ln(1 + 0) = 0 .
x→0	x→0

140

Лекции 12 – 13

13.1.7. Свойства функций, непрерывных на отрезке

Если f (x) непрерывна на

[a,b], то она

ограничена на этом отрезке

( M и m : m ≤ f (x) ≤ M x [a,b]).

Пример:

f (x) = sin x, 0,

m = −1, m = −5, m

= 0,

M = 2, M = 3,

M =1,

m = inf {f (x)}= 0, M = sup{f (x)}=1,

!Требование непрерывности на отрезке является обязательным, так как функция, непрерывная на интервале, может и не быть ограниченной.

Пример:

f (x) = 1x непрерывна на интервале (0, 1), то есть

x , 0 < x <1. f (x) - не ограничена.

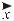
ТЕсли f (x) непрерывна на [a,b], то она достигает на нем своих точной

верхней и точной нижней граней

( x1 [a, b]: f (x1 ) = M , x2 [a, b]: f (x2 ) = m ).

Доказательство:

От противного: если нет точки

x1 f (x) < M

f (x) − M

< 0 или

− f (x) > 0 .

, F(x) - непрерывна на [a,b] (по теореме о

Рассмотрим F(x) =

− f (x)

непрерывности сложной функции).

[a,b],

Из непрерывности F(x) следует ее ограниченность на

F(x) =

−

≤ B f (x) ≤ M

M − f (x)

−

- неточная верхняя грань. Полученное

- верхняя грань, тогда M

противоречие доказывает теорему.

Замечательные пределы. Непрерывность функции

141

Пример:

) =1 .

= 0,

M = f (

f (x) = sin x , x 0,

m = f (0)

f (x) =

, x [−1,1].

=1 .

m = 0, M

!1). Для интервалов (a,b) и полуинтервалов [a,b) или (a,b] теорема не справедлива.

Пример:

y = x, (0,1) .

Значения m = 0 и M =1 - не достигаются на x (0,1) .

2). Для f (x) , непрерывной на [a,b], m и M можно назвать наименьшим и наибольшим значениями функции:

max f (x) = M ,min f (x) = m.

ТЕсли функция y = f (x) непрерывна на [a,b] и имеет на концах отрезка значения f (a) и f (b) разных знаков, то найдется точка ξ (a,b) такая, что f (ξ) = 0.

Доказательство:
Пусть f (a) < 0, f (b) > 0 . Рассмотрим {x}: f (x) < 0 , {x}	- ограничено
сверху, например, числом b sup{x} =ξ . Покажем, что	f (ξ) = 0.

Если бы f (ξ) = C > 0 , тогда по теореме о сохранении знака непрерывной

функции существовала бы δ -окрестность точки ξ : x (ξ −δ,ξ +δ) f (x) > 0 , но тогда бы ξ не являлась бы точной

верхней гранью sup{x}, где f (x) < 0 . Аналогично для f (ξ) = C < 0 остается f (ξ) = 0, что и требовалось доказать.

ТТеорема о прохождении непрерывной функции через любое промежуточное значение. Если функция y= f (x) - непрерывна на [a,b], имеет на

концах отрезка значения f (a) = A, f (b) = B и число С расположено между числами А и В : A < C < B , то найдется точка ξ (a,b) такая, что f (ξ) = C .

142	Лекции 12 – 13
Доказательство:
Рассмотрим:	C : A < C < B, F(x) = f (x) −C F(a) < 0, F(b) > 0. F(x) -
непрерывна	на [a,b]. По предыдущей теореме ξ (a,b) ,

F(ξ) = 0 f (ξ) −C = 0 f (ξ) =C , что и требовалось доказать.

!Теорема применяется для отыскания корней уравнения вида F(x) = 0 методом половинного деления отрезка.

Пример:

Имеет ли корень уравнение sinx – x + 1 = 0?

Рассмотрим функцию f(x) = sinx – x + 1, которая непрерывна на всей числовой оси, поскольку является суммой непрерывных функций.

f(0) =1>0, f(2π) = -2π + 1 < 0. Следовательно, внутри отрезка [0, 2π] имеется, по крайней мере, один корень исходного уравнения.

Пример:

Принимает ли функция	f (x) =	x3	−sin π x +3 значение 2	1	внутри отрез-
		4		3

ка [-2, 2]?

Функция является непрерывной на [-2, 2]. На концах отрезка функция принимает числовые значения f(-2) = 1, f(2) = 5.

Так как 1 < 2	1	< 5,	то ξ (-2, 2) такая, что	f (ξ) = 2	1 .
	3				3

13.2. Точки разрыва и их классификация

Точка x0, в которой функция y = f(x) обладает свойством непрерывности, называется точкой непрерывности функции, в противоположном случае точка x0 называется точкой разрыва функции.

Для классификации точек разрыва удобно использовать третье определение непрерывности.

О	Если	односторонние	пределы	существуют,	причем
	lim	f (x) = lim f (x), а функция y = f(x) не определена в точке x0, или
	lim
	x→x0 −0	x→x0 +0

lim f (x) ≠ f (x0 ), то точка x0 называется точкой устранимого разрыва.

x→x0

!Устранимый разрыв можно устранить, вводя функцию

	f (x),		x ≠ x ,
f1			0
	(x) = lim f (x), x = x .
		0	0
	x→x

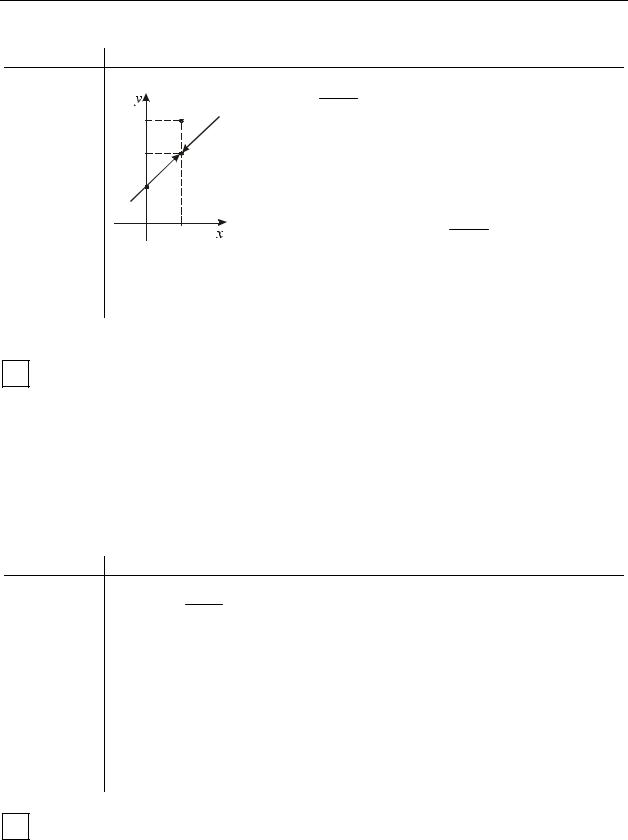
Замечательные пределы. Непрерывность функции								143
Пример:
			2	−4 , x ≠ 2,
		x		−4 , x ≠ 2,
5		f (x) = x		−2
5				x = 2.
		5,		x = 2.
4		Точка x = 2 - точка устранимого разрыва, посколь-
		Точка x = 2 - точка устранимого разрыва, посколь-
2		ку lim f (x) = lim			f (x) = 4 ,		f (2) = 5 ≠ 4 .
		x→2+0		x→2−0
0	2					2	−4	, x ≠ 2,
0	2	Устраним разрыв:			x		−4	, x ≠ 2,
		Устраним разрыв:			f1 (x) = x		−2
								x = 2.
					4			x = 2.
Функция	f1 (x) непрерывна всюду.

ОЕсли: 1) x0 – точка разрыва f (x) ,

2)существуют конечные пределы справа и слева:

	lim		f (x), lim f (x) ,
	x→x0	+0	x→x0	−0
3) lim f (x) ≠	lim	f (x),
x→x0 +0	x→x0 −0

то точка x0 называется точкой разрыва 1-го рода (неустранимый конечный скачок).

Пример:

y = f (x) = 1 1 , x = 0 - точка разрыва f (x) .

1+ 2x

x → +0,

x → −0,

lim

→ +∞,

= 0 . lim

→ −∞, =1.

x→0+0

x→0−0

+ 2x

→ +∞.

+ 2 x

→ 0.

x= 0 - точка разрыва первого рода.

ОЕсли хотя бы один из односторонних пределов не существует или бесконечен, то точка х0 называется точкой разрыва 2-го рода.

144	Лекции 12 – 13

Пример:

	f (x) =	1	, x = 0 -	точка разрыва 2-го рода; так
		x	f (x) = +∞ ,		f (x) = −∞.
	как lim		f (x) = +∞ ,	lim	f (x) = −∞.
0	x→0+			x→0−
0	.
	.

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

методы практического вычисления пределов;

замечательные пределы;

эквивалентные бесконечно малые;

различные определения непрерывности;

свойства непрерывных функций;

классификацию точек разрыва.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ

Целью этого раздела является исследование поведения функции y = y( x) в окрестности точки x по ее числовым характеристикам в самой этой точке.

Лекции 14 - 15 ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ

В лекциях 14 – 15 излагаются основные понятия дифференциального исчисления – понятия производной и дифференциала, рассматривается их геометрический и механический смысл. Выведены правила и формулы дифференцирования, указаны методы вычисления производных для различных способов задания функций. Показано практическое применение дифференциала в приближенных вычислениях.

14.1.Производная функции.

14.1.1.Определение производной функции

14.1.2.Геометрический смысл производной. Уравнения касательной и нормали к графику функции

14.1.3.Механический смысл производной

14.2.Правила и формулы дифференцирования

14.2.1.Производная суммы, разности, произведения и частного функций

14.2.2.Производная обратной функции

14.2.3.Таблица производных

14.2.4.Производная сложной функции

14.2.5.Логарифмическая производная

14.2.6.Производная неявной функции

14.2.7.Производная функции, заданной параметрически

15.1.Производные высших порядков

15.1.1.Определение производной n-го порядка

15.1.2.Правила вычисления производной n-го порядка

15.1.3.Вторая производная от неявной функции

15.1.4.Вторая производная от параметрически заданной функции

15.1.5.Механический смысл второй производной

15.2.Дифференциал функции

15.2.1.Дифференциал независимой переменной

15.2.2.Свойства дифференциалов

15.2.3.Геометрический смысл дифференциала

15.2.4.Применение дифференциала к приближенным вычислениям

15.2.5.Дифференциал сложной функции

15.2.6.Дифференциалы высших порядков

146	Лекции 14 – 15
14.1. Производная функции

14.1.1. Определение производной функции

Пусть y = f (x) определена на (a,b) и x (a,b) - некоторая фиксированная точка, ∆x - приращение аргумента в точке x , ∆y = f (x + ∆x) − f (x) - со-

∆y

ответствующее приращение функции, ∆x - отношение приращений (зависит от ∆x , x - фиксировано).


							∆y
О	Производной функции f (x) в точке x		называется			lim		при условии,
						∆x→0	∆x

	что он существует. Обозначение:	y′ = dy	= lim	∆y	= lim		f (x + ∆x) − f (x)		.
				∆x
		dx	∆x→0			∆x→0		∆x

ОФункция f (x) называется дифференцируемой в точке x , если производная y′(x) существует; операция нахождения производной называется

дифференцированием.

ОФункция f (x) называется дифференцируемой на интервале (a,b), ес-

ли она дифференцируема в каждой точке этого интервала.

Найдем, исходя из определения, производные некоторых элементарных функций.

Пример:

y = sin x, y′ = ?

′	sin(x + ∆x) −sin x	0		= lim
y (x) = lim	∆x	=	0	= lim
∆x→0	∆x		0	∆x→0

		∆x	sin	∆x
	cos x +	2	sin	2
= lim		2		2	= cos x, т.к. lim
= lim		∆x			= cos x, т.к. lim
∆x→0		∆x			∆x→0
		2

(sin x)′ = cos x .

2 cos x + ∆2x sin ∆2x = ∆x

sin ∆x

∆x2 =1 . 2

Пример:

y(x) = loga x, 0 < a ≠1

′

, y (x) = ?

x +∆x

∆x

∆y = loga (x +∆x) −loga

x = loga

= loga 1

∆x

loga 1+

∆x

y′ = lim

∆x

= lim loga 1

∆x

∆x→0

Производная и дифференциал

147

∆x

x x

= loga

∆x

lim

= loga lim

∆x→0

1		1 loga e .
loga ex	=	1 loga e .
		x

(loga x)′ = 1x loga e , (ln x)′ = 1x .

Пример:

y = xα ;

y′ = (xα )′ = lim (x + ∆x)α − xα .

∆x→0 ∆x

Без ограничения общности можем считать α натуральным показателем и раскрыть скобку, как бином Ньютона:

lim (x + ∆x)α

− xα

= lim

xα + α xα−1 ∆x +α (α −1)xα−2 ∆x2

+ ... − xα

∆x

∆x→0

∆x

∆x→0

= lim α xα−1

∆x + α (α

−1)xα−2 ∆x2

+ ...

= lim α xα−1

+ o(∆x)

=α xα−1 .

∆x

{

}

∆x→0

14.1.2.Геометрический смысл производной. Уравнения касательной

инормали к графику функции

Рассмотрим две точки графика функции f (x) : M (x, f (x)) и P(x + ∆x, f (x + ∆x)) . MP -

секущая.

При стремлении ∆x к нулю (т.е. при стремлении точки P к точке M ) эта секущая будет поворачиваться относительно точки M .

О	Касательной к	графику	функции
	y = f (x) в точке	M (x, f (x))	называется предельное положение секу-

щей при ∆x → 0 ( P → M ).

ОНормалью к графику функции y = f (x) в точке M (x, f (x)) называется перпендикуляр к касательной, проведенный через точку касания.

ТЕсли функция y = f (x) имеет в точке x производную f ′(x) , то график функции в точке M (x, f (x)) имеет касательную с угловым коэффициентом f ′(x) .

148								Лекции 14 – 15
Доказательство:			∆y
Пусть		tgϕ(∆x) =	∆y	и	∆x →0 .	Так	как	существует
	∆y		∆x
lim	∆y	′			1) существует предельное положение
lim	∆x	= f (x) = lim tgϕ(∆x) , то:			1) существует предельное положение
∆x→0	∆x	∆x→0

секущей, то есть касательная; 2) угловой коэффициент касательной равен f ′(x) .

С1). Значение y′(x0 ) позволяет записать уравнение касательной к кри-

вой y = y(x) в точке x0 :
y − y0 = y′(x0 ) (x − x0 ).
2). Поскольку условие	перпендикулярности прямых: k1 k2 = −1, то
уравнение нормали имеет вид:
y =	f (x0 ) +	−1	(x − x0 ) .
y =	f (x0 ) +	f ′(x0 )	(x − x0 ) .
		f ′(x0 )

3). При y′(x)> 0 в точке x функция является возрастающей, а при y′(x)< 0 – убывающей.

14.1.3. Механический смысл производной

	Рассмотрим движение точки по прямой. S = f (t)							- перемещение точки в
момент времени t ,					′	f (t + ∆t) − f (t)	-	мгновенная скорость в
				V = f (t) = lim
				V = f (t) = lim		∆t
момент времени t .					∆t→0	∆t
момент времени t .
	Пример:
	Пример:
		S (t )=	gt2		, V (t) =S '(t )= gt .
		S (t )=			, V (t) =S '(t )= gt .
				2

14.2. Правила и формулы дифференцирования

14.2.1.Производная суммы, разности, произведения и частного функций

1)(c)′ = 0 , c = const ;

2)( f (x) ± g(x))′ = f ′(x) ± g′(x) ;

3)(c f (x))′ = c f ′(x) ;

4)( f (x) g(x))′ = f ′(x) g(x) + g′(x) f (x) ;

	f (x)	′		′		′
5)			=	f (x)g(x) − g (x) f (x)			.
	g(x)			g	2	(x)

Производная и дифференциал

149

Доказательство правила 2:

lim ( f + ∆f )+(g + ∆g )−( f + g )

∆x→0

∆x

= lim

f + ∆f − f

+ lim

g +∆g − g

∆x

∆x→0

∆x

∆x→0

= lim

∆f

+ lim

∆g

= f + g

∆x→0

∆x

∆x→0

∆x

Пример:

′

y = 3sin x +5log2 x −10 ,

= 3cos x +5 x log2 e .

14.2.2. Производная обратной функции


Т	Пусть f (x)
	1)	строго монотонна и непрерывна в окрестности точки x0 ,

2)		функция дифференцируема в точке x0 и f ′(x0 ) ≠ 0 ,
	тогда:
1)		существует производная обратной функции в точке x0 : (f −1( y))′;
	2) (f −1( y))′y=y0 =		1	.

f ′(x0 )

Доказательство:

Из условия 1 следует существование непрерывной строго монотонной обратной функции x = f −1 ( y) . Рассмотрим x = f −1 ( y) в окрестности точки y0 = f (x0 ) . Зададим приращение аргументу ∆y ; ему соответствует

приращение функции ∆x и ∆∆yx = ∆1y (*).

∆x

Из строгой монотонности f −1 ( y) при ∆y ≠ 0 следует, что ∆x ≠ 0 . Устре-

мим ∆y →0 , из непрерывности				x = f −1 ( y) ∆x → 0 . Но при ∆x → 0 ,
∆y → f ′(x0 ) , следовательно,	∆x			→		1	.
	∆y				f ′(x0 )
∆x				1
Таким образом, (f −1( y))′y=y0	=					.
		f	′(x0 )

150									Лекции 14 – 15
Пользуясь этой формулой, найдем производные некоторых элементар-
ных функций.
1) y = ax , (ax )′ = ? a > 0, a ≠ 0					. x = loga y ;
(ax )′ =	1	=		1	=	y	=	ax	= ax ln a ;
(ax )′ =	′	=	1		=	loga e	=	loga e	= ax ln a ;
	(loga y)		y	loga e		loga e		loga e
	(loga y)			loga e

(ax )′ = ax ln a , (ex )′ = ex .

2)y = arcsin x , (arcsin x)′ = ? x = sin y ,

(arcsin x)′ =

;

(sin y)′

cos y

1 −sin2 y

1 − x2

(arcsin x)′ =

1 − x2

3) (arccos x)′ = −

1 − x2

4) y = arctg x, (arctg x)′ = ?

x = tg y , (tg y)′ =

;

cos2 y

(arctg x)′ =

= cos

y =

;

(tg y)′

1 + tg2 y

1 + x2

(arctg x)′ = 1+1x2 .

5)(arcctg x)′ = −1+1x2 .

14.2.3. Таблица производных

Таблица получена, исходя из определения производной и правил дифференцирования.

1.(xα )′ =α xα−1 .

2.(ax )′ = ax ln a (a > 0, a ≠1) (ex )′ = ex .

3.	(loga x)′ = loga e	1	(a > 0,a ≠1) (ln x)′ =	1 .
	(sin x)′ = cos x .	x		x
4.	(sin x)′ = cos x .
5.	(cos x)′ = −sin x .

Производная и дифференциал

151

6.(tgx)′ = cos12 x .

7.(ctgx)′ = −sin12 x .

10.(arctgx)′ = 1 +1x2 .

11.(arcctgx)′ = −1 +1x2 .

12.(shx)′ = chx .

13.(chx)′ = shx .

14.(thx)′ = ch12 x

15.(cthx)′ = sh12 x

= ex −e−x

Гиперболический синус shx .

= ex + e−x

Гиперболический косинус chx .

Гиперболический тангенс	thx = shx .
	chx

= chx

Гиперболический котангенс cthx shx .

14.2.4. Производная сложной функции

Если:

1) y = f [ϕ(t)]

- сложная функция, t- независимая переменная,

ϕ -

промежуточный

аргумент;

2) существуют

f ′(x ) и

ϕ′(t0 ) , где

x0 =ϕ(t0 ) , то {f [ϕ(t)]}′ = f ′(x0 ) ϕ′(t0 ) .

Доказательство:

Рассмотрим:

t0 +∆t ∆x =ϕ(t0 +∆t) −ϕ(t0 ) , ∆x ∆y = f (x0 +∆x) − f (x0 ).

Пусть ∆t →0 , тогда lim

∆x

(см. условие f ′(x0 ) = y′(x0 ) ).

Вычислим:

∆t→0

∆t

lim

∆y

= lim

∆y

∆x = lim

∆y

lim

∆x = f ′(x0 ) ϕ′(t0 ) ,

что и

требовалось

∆t→0

∆t

∆t→0

∆x

∆t

∆t→0

∆x

∆t→0

∆t

доказать.

!Независимой переменной была t , промежуточным аргументом - x . На практике чаще имеем дело с функциями вида: y = f (u), u =ϕ(x) , тогда

152

Лекции 14 – 15

′ = y

′u ′. Например,

y = earctg x ;

y = eu , u = arctg x, y

′

= ? Решение:

y ′

= eu , u

′

y ′ = earctg x

2 .

1 + x

+ x

14.2.5. Логарифмическая производная

При вычислении производной некоторого выражения полезно предвари-

тельное логарифмирование этого выражения.

Рассмотрим функцию y = f (x), y′ = ?

ln y = ln f (x), [ln y]x′ =

y′;

y′

- называется логарифмической производной.

Отсюда y′ = y [ln y]′.

Пример:

1) y = xα , α ≠ 0, y′ = ?

ln y =α ln x,

y′

=α

1 .

xα

′

α−1

y′

y α

x , y′ =α

, (x

)

=α x

y = (sin x)x2

, y′ = ? ln y = x2 ln(sin x) ,

y′

= 2x ln(sin x) + x2

cos x .

sin x

{

}

′

2x ln(sin x) + x

ctg x (sin ) .

Пример:

В общем случае для степенно-показательных выражений.

y = f (x)ϕ( x) ln y =ϕ( x) ln f ( x) .

y′ = f (x)ϕ( x) ϕ′(x) ln f (x) +ϕ( x)	f ′(x)	.
	f (x)

Пример:

Логарифмическая производная применяется для вычисления производной произведения большого числа сомножителей.

1). y = sin x cos x x, y′ = ? ln y = ln sin x +ln cos x +ln x .

y′		cos x		−sin x		1		1
	=		+		+		y′ = sin x cos x x ctg x − tg x +
y	=	sin x	+	cos x	+	x	y′ = sin x cos x x ctg x − tg x +
y		sin x		cos x		x		x

Производная и дифференциал

153

2). y = 5 x3 (x −1)7

, y′ = ?

x + 6

ln y =

3ln x + 7ln

(x −1)

− ln (x + 6) ;

′

(ln y)

−

;

x −1

x +

y′ =

x3 (x −1)7

−

x −1

+ 6

x + 6

14.2.6. Производная неявной функции

Пусть уравнение F

(x, y (x))= 0 задает неявно функцию y = y(x).

Для

вычисления

y′(x)

нужно

продифференцировать

тождество

F (x, y) = 0 по переменной

x , рассматривая функцию F (x, y (x))

как слож-

ную

функцию

аргумента

x , а

затем

полученное

уравнение

(x, y (x), y′(x))= 0 разрешить относительно y′(x).

Пример:

x2 y2

′

a2 + b2 =1, y

= ? ( y > 0) .

Решение:

Первый способ. Выразим явно y из уравнения:

y = ± b

− x2

. Так как y > 0 ,

y = b

a2 − x2

y′ =

(a2

− x2 )−2 (

−2x)= −

= − b2

a 2

a2 − x2

Второй способ.

Продифференцируем выражение

=1 по пере-

менной x :

2 y

y′ = 0 , откуда y′ = −

!Выражение для производной y′(x) может зависеть как от x , так и от y .

14.2.7. Производная функции, заданной параметрически

154		Лекции 14 – 15
Пусть функция	x = x(t)	.
Пусть функция	y = y(x)задана параметрически:	.
	y = y(t)

ТЕсли: 1) x(t), y(t) - дифференцируемы, 2) x = x(t) имеет обратную функ-

′

цию t = t(x), t (x) , 3)

x (t) ≠ 0 , то

′

Доказательство:

y = y(t), t = t(x) . Рассматривая t как промежуточ-

Рассмотрим функции:

ный аргумент, можно считать, что

- сложная функция x . Тогда

′ = y

′ t

′, t ′ =

y ′ =

yt′

x ′

Пример:

x = t2 , y = t3 , yx′ = ?

Решение: xt′ = 2t, yt′ = 3t2 , yx′ = 3t2 = 3 t . 2t 2

15.1. Производные высших порядков

15.1.1. Определение производной n-го порядка

ОПроизводной второго порядка от функции y = f (x) называется произ-

водная от ее первой производной. Обозначение: f ′′(x) = ( f ′(x))′.

Производной n -го порядка (или n–й производной) называется произ-

водная первого порядка от производной (n −1)-го порядка.:

f (n) (x) = (f (n−1) (x))′.Также используют обозначение y(n) (x) = d n y . dxn

Пример:

1)y = sin x, y′ = cos x, y′′ = −sin x, y′′′ = −cos x .

2)y = xn , y′ = nxn−1, y′′ = n(n −1)xn−2 ,…, y(n) = n!, y(n+1) = 0 .

15.1.2.Правила вычисления производной n-го порядка

1.[ f (x) + g(x)](n) = f (n) (x) + g(n) (x) .

2.Формула Лейбница (производная произведения):

Производная и дифференциал

155

[ f (x) g(x)](n) = ∑Cnk f (n−k )

k =0

из n по k , k! (читается k ных k , причем (k +1)! = (k

(x) g(k ) (x) , где Cnk =	n!	- число сочетаний
	k!(n − k)!

- факториал) определен для целых неотрицатель-

+1) k!, 0! =1! =1.

Пример:

Найти n–ю производную от функции y = eax x2 . Решение:

y = f (x) g(x); где

f (x) = eax ; g(x) = x2

f (x) = eax ;

g(x) = x2 ;

′

;

′

(x) = a e

g (x) = 2

′′

;

′′

(x) = a

g (x) = 2;

′′′

(x) = 0;

f (n) (x) = an eax ;

g(n) (x) = 0.

Таким образом, в формуле Лейбница всего 3 ненулевых члена.

Вычисляем коэффициенты:

k =

0 → Cn0 =

=1;

k =

1 → Cn1 =

= n;

1!(n −1)!

k =

2 → Cn2 =

n(n −1)

;

2!(n − 2)!

y(n) (x) = an eax x2 + nan−1eax 2x + n(n −1) an−2 eax 2.

15.1.3. Вторая производная от неявной функции

Рассмотрим

неявную

функцию

y = y (x),

определяемую

уравнением

F(x, y) = 0 . Для

отыскания

второй

производной

соотношение

F(x, y) = 0

дифференцируем два раза по переменной x , считая

функцией x , и выра-

жаем y′′ как функцию y и x .

Пример:

x2 + y2 =1, y′′ = ?

2x + 2 y y

′

+ 2 y y

′′

= 0 ,

= 0,

= −

2 y = − y , 2 +

2 y

′′

1 + (y′)2

+ x2

= −

y3 .

156	Лекции 14 – 15

15.1.4. Вторая производная от параметрически заданной функции

x = x(t)

Рассмотрим

y = y(t)

′ ′

(y′x )′

или

′′

y′

′

′′x

′ − x

′′y ′

′′

x =

yxx = (yx ) x =

yxx =

(xt′)

xt′

Таким образом,

yxx′′ =

′′x ′ −

′′y ′

tt t

(xt′)3

15.1.5. Механический смысл второй производной

Пусть

S = f (t)

- закон

движения

тела, движущегося поступательно.

Скорость тела V (t ) в данный момент времени:

V (t )= f ′(t) . Если движение

неравномерно, то для приращения времени ∆t

приращение скорости состав-

ляет∆V .

Тогда

∆V

- среднее ускорение тела за промежуток времени ∆t . При ∆t → 0

∆t

получим ускорение в данный момент времени t :

= lim

∆V

=V ′(t) .

a(t )=

f ′′(t)

∆t→0

∆t

Таким образом,

ускорение прямолинейного движения равно

второй производной от перемещения по времени.

15.2. Дифференциал функции

15.2.1. Правила вычисления производной n-го порядка

x (a,b)

Если

функция y = f (x)

дифференцируема на

(a,b), то

lim

∆y

′

∆y

при

∆x → 0 стремится к числу f

′

∆x

= f (x) . Отношение

∆x

(x) , следо-

∆x→0

∆y

вательно,

отличается

от f

′

на

бесконечно малую α (x):

∆x

(x)

∆y

′

(x)=

′

∆x

= f (x) +α(x), причем lim α

0 , или ∆y = f (x) ∆x +α(x) ∆x .

∆x→0

Рассмотрим

′

бесконечно

f (x)∆x . В общем случае

(x) ≠ 0 ,

f (x)∆x -

малая величина первого порядка относительно ∆x при ∆x → 0 .

Производная и дифференциал		157
Поскольку lim	α (x) ∆x	= lim α (x)= 0 , тоα (x) ∆x - бесконечно малая вели-
	∆x
∆x→0		∆x→0

чина более высокого порядка, чем ∆x .

ОГлавная, линейная по ∆x часть приращения функции называется дифференциалом функции в точке x и обозначается dy = f ′(x) ∆x .

!Главная часть, потому что α(x) ∆x - бесконечно малая более высокого

порядка малости, чем ∆x . Линейная, потому что дифференциал зависит от ∆x в первой степени.

15.2.2. Дифференциал независимой переменной

Пусть y = x . Тогда ∆y = ∆x, y′ = (x)′ =1, dy = dx = ∆x .

Вывод: дифференциал независимой	переменной равен ее приращению,
′	′

dx = ∆x . В общем случае: dy = f (x)∆x = f (x)dx .

dy = f ′(x)dx .

СПроизводная может быть записана как отношение дифференциала функции к дифференциалу независимого переменного (так называемые обо-

значения Лейбница): f ′(x) = dydx

15.2.3. Свойства дифференциалов

Поскольку дифференциалы функций вычисляются по основной формуле dy = y′(x) dx , то справедливы обычные правила дифференцирования.

1.d (c)= 0 ;

2.d (u ± v)= du ± dv;d (u ± c)= du ;

3.d (uv)= udv + vdu;d (uc)= cdu ;

4.	u	=	vdu −udv		.
	d		v	2
	v

15.2.4. Геометрический смысл дифференциала

Рассмотрим функцию y = f (x) . Обозначения, приведенные на рисунке, соответствуют:

′	′	, MT - ка-
M (x, y), M (x + ∆x, y + ∆y) , ∆y = NM

сательная в точке M .

Рассмотрим ∆MNT :

MN = ∆x, NT = ∆x tgϕ , NT = ∆x f ′(x) , dy = NT .

158	Лекции 14 – 15
Дифференциал функции y = f (x) в точке	x есть приращение ординаты каса-
тельной к графику функции в точке x .

15.2.5. Применение дифференциала к приближенным вычислениям

Метод основан на замене приращения функции ∆y = f (x + ∆x)− f (x) приближенно дифференциалом этой функции: ∆y dy = f ′(x)dx .

Это возможно, так как ∆y и dy отличаются на бесконечно малую вели-

чину o(∆x). lim	∆y	=1 + lim	α∆x	=1 + lim	α	=1.
	dy		f (x)∆x		f (x)
∆x→0		∆x→0		∆x→0
			′		′

Основные рабочие формулы:

x = x0 + ∆x ,

f (x) = f (x0 + ∆x) ≈ f (x0 ) + dy , f (x0 + ∆x) ≈ f (x0 ) + f ′(x0 )∆x .

Геометрический смысл: истинная функция на отрезке [x0 , x0 ется линейной функцией, график которой – касательная в точке

+ ∆x] заменя-

(x0 , f (x0 )).

Пример:

Вычислить приближенно 4 15,8 . Решение:

Пусть y = 4 x , x0 =16 . Тогда y(16)= 4 16 = 2 ;

y = (15,8)= y(16)+ ∆y ; заменим ∆y ≈ dy = y′(x)∆x ;

∆x =16 −15,8 = −0,2 ;

y′(x)= x 14 ′ = 14 x 14−1 = 14 x−3 4 ; y′(16)= 14 16−34 = 418 = 321 .

Тогда y(15,8)= 2 + 321 (− 0,2)= 2 − 0,0062 =1,9938 .

Пример:

Вычислить приближенно значение объема V шара радиусом r =1,02 м. Решение:

Так как V (r)=	4	π r 3	, то, полагая r0 =1 , ∆r = 0,02	, V ′(r )= 4πr2	и ис-
	3

пользуя формулу для ∆V , получаем:

V (1,02) =V (1)+ ∆V ≈V (1)+V ′(1) 0,02 = 43 π + 4π 0,02 4, 44 м3.

Производная и дифференциал

159

15.2.6. Дифференциал сложной функции

Рассмотрим сложную функцию y = f [ϕ(x)], Пусть u – промежуточный аргумент: y = f (u), u =ϕ(x) . yx′ = fu′ ux′ умножим это равенство на dx :

yx′dx = fu′ ux′ dx , dy = fu′du .

Сравнение с dy = fx′dx показывает, что дифференциал функции сохраняет

свою форму независимо от того, является ли ее аргумент x независимой переменной или функцией независимой переменной (промежуточным аргументом).

Это свойство называется свойством инвариантности (неизменности) формы первого дифференциала.

15.2.7. Дифференциалы высших порядков

Пусть y = f (x) - дифференцируемая функция, а ее аргумент x - независимая переменная. Тогда ее первый дифференциал dy = f ′(x)∆x = f ′(x)dx

также является функцией x , от которой в свою очередь можно найти дифференциал.

ОДифференциалом второго порядка (или вторым дифференциалом)

функции f (x) называется дифференциал ее дифференциала при фиксированном dx .

d 2 f (x) = d (df (x)) = d ( f ′(x)dx) = dx d ( f ′(x)) = dx f ′′(x)dx = f ′′(x) (dx)2 =

′′	2	; d	2	f (x) =	′′	2	.
= f (x)dx		; d		f (x) =	f (x)dx		.
Аналогично				определяется				дифференциал	порядка	n:
d n f (x) = d (d n−1 f (x)).					Можно показать, что d n f (x) = f (n) (x)dxn .					Здесь

dxn = (dx)n .

!1. Для независимой переменной d 2 x = 0, d 3 x = 0,…

2. В приведенных формулах предполагалось, что x - независимая переменная. Если x - промежуточный аргумент, то форма для второго диф-

ференциала будет другой, отличной от выражения d 2 f = f ′′(x)dx2 . Покажем это на примере второго дифференциала. Пусть y = f (x),

x = g (t ), t - независимая переменная.

Тогда

d 2 f = d (df )= d ( f ′(x) dx)= d ( f ′(x)) dx + f ′(x) d (dx)=

160	Лекции 14 – 15
	= f ′′(x) dx2 + f ′(x) d 2 x = f ′′(x) (g′(t ))2 dt2 + f ′(x) g′′(t ) dt2 .

Таким образом, в случае сложной функции в выражении для второго дифференциала появляется дополнительное слагаемое; форма второго дифферен-

циала не инвариантна.

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

понятия производной и дифференциала, их геометрический и механический смысл;

правила и формулы дифференцирования;

таблицу производных;

способы вычисления производных от сложных функций;

функций, заданных неявно и параметрически;

таблицу производных;

производные высших порядков и правила их вычисления;

применение дифференциала к приближенным вычислениям.

Лекция 16 ОСНОВНЫЕ ТЕОРЕМЫ АНАЛИЗА.

ПРАВИЛО ЛОПИТАЛЯ – БЕРНУЛЛИ. ФОРМУЛА ТЕЙЛОРА

В лекции 16 рассмотрены основные теоремы анализа (Ролля, Лагранжа и Коши), широко использующиеся практически во всех разделах анализа. Излагается правило раскрытия неопределенностей Лопиталя – Бернулли, позволяющее вычислять пределы с помощью дифференцирования. Выводится формула Тейлора, которая при достаточно широких предположениях относительно вида функции дает возможность представить ее приближенно в виде многочлена и оценить допускаемую при этом погрешность.

16.1.Основные теоремы анализа.

16.1.1Теорема Ролля (о нуле производной)

16.1.2.Теорема Лагранжа (теорема о конечных приращениях)

16.1.3.Теорема Коши (обобщенная теорема о конечных разностях)

16.1.4.Правило Лопиталя – Бернулли. Применение правила Лопиталя для раскрытия неопределенностей

16.1.5.Формула Тейлора. Частные случаи формулы Тейлора. Разложение по формуле Маклорена некоторых элементарных функций Оценка остаточного члена. Приложения формул Тейлора и Маклорена

16.1.Основные теоремы анализа

16.1.1. Теорема Ролля (о нуле производной)

ТЕсли: 1) функция f (x) - непрерывна на отрезке [a,b], 2) на интервале (a,b) существует производная f ′(x) , 3) значения функции на концах от-

резка совпадают,	f (a) = f (b) , то существует точка ξ (a,b)		такая, что
′
f (ξ) = 0 .
Доказательство:	f (x) непрерывна на [a,b],
Так как функция	f (x) непрерывна на [a,b],	то на отрезке существуют
наибольшее M и наименьшее m значения функции.
Возможны два случая: 1) M = m и 2) M > m .			′
Рассмотрим: 1)	M = m , f (x) - постоянная,	следовательно,	′
Рассмотрим: 1)	M = m , f (x) - постоянная,	следовательно,	f (x) = 0

x (a,b);

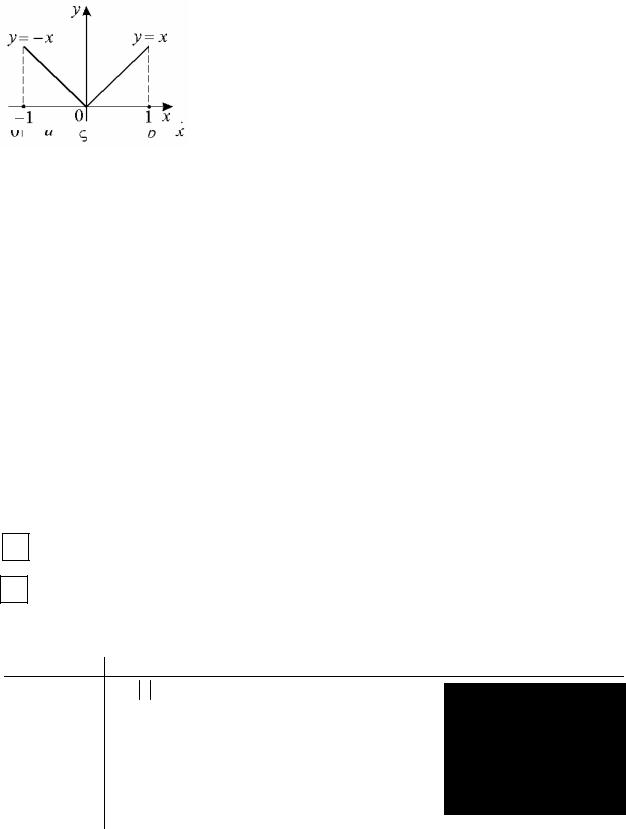
162

Лекция 16

2) M > m ,

следовательно, хотя бы одно из этих значений достигается

внутри [a,b], так как f (a) = f (b) .

Пусть f (ξ) = M , ξ (a,b).

Так как

f (ξ) - наибольшее значение

функции, то f (ξ +

x)− f (ξ )≤ 0 при лю-

бом знаке

x .

f (ξ + x)− f (ξ )

≤ 0,

x > 0 ,

f (ξ + x)− f (ξ )

≥ 0, x < 0

переходя к пределу

x →0 и рассматривая отдельно правый и левый

пределы, получаемlim

f (ξ +

x)− f (ξ )

= f ′(ξ ) ≤ 0 ,

x > 0 ,

x→+0

lim

f (ξ +

x)− f (ξ )

= f ′(ξ )≥ 0 ,

x < 0 .

x→−0

′

Эти соотношения совместимы, если f

(ξ) = 0 .

Доказательство для случая, когда во внутренней точке отрезка достигается минимум, проводится аналогично.

Геометрический смысл теоремы Ролля

Если функция удовлетворяет условию теоремы Ролля, то в некоторой точке отрезка касательная к графику параллельна оси 0x .

СТеорема Ролля позволяет узнать об обращении производной в ноль без ее вычислений.

!Если f (x) такова, что производная существует не во всех точках внутри отрезка [a,b], то может не оказаться такой точки ξ , в которой f ′(ξ) об-

ращается в ноль.

Пример:

y = x ,

(y0прав )′ =1,

(y0лев )′ = −1.

y′(0) не существует (по определению).

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

163

16.1.2. Теорема Лагранжа (теорема о конечных приращениях)

ТЕсли: 1) f (x) - непрерывна на отрезке [a,b], 2) на интервале (a,b) существует производная f ′(x) , то существует, по крайней мере, одна точ-

	ка ξ (a,b) такая, что							′
							f (b)− f (a) = f (ξ) (b −a).
	Доказательство:
	Обозначим			f (b)− f (a)				= Q . Построим F (x)= f (x)− f (a)−Q (x −a).

					b − a
	F (x) обладает следующими свойствами: 1) непрерывна на [a,b],
	2) F′(x) на (a,b), 3) F (a)= F (b)= 0 .
	Из теоремы Ролля следует, что существует точка ξ (a,b) такая,								что
	F′(ξ) = 0 , F′(x)= ( f (x)− f (a)−Q(x − a))′, F′(x)= f ′(x)−Q = 0, урав-
	нение		f ′(x)−Q = 0				имеет решение x =ξ , т.е. f ′(ξ ) = Q ,		или
	f	′(ξ ) =	f (b)− f (a)			.

				b − a
Геометрический смысл теоремы Лагранжа
CB	=	f (b)− f (a)			- угловой коэффициент се-
AC
		b − a

кущей AB .

f ′(ξ) - угловой коэффициент касательной к кривой y = f (x) в точке x =ξ . На кривой AB

найдется, по крайней мере, одна точка M , в которой касательная параллельна хорде AB .

!1). Доказанная формула называется формулой Лагранжа или форму-

лой конечных	приращений. Так как		a <ξ <b,	то ξ − a <b − a ,
ξ −a =θ (b −a),	где	0 <θ <1,	откуда	ξ = a +θ(b − a) ,
f (b)− f (a)= f ′ a +θ (b		− a) (b − a).

2). Точек ξ может быть несколько.
3). Если f (a)= f (b), то		f ′(ξ )= 0 , получаем утверждение теоремы Рол-

ля.

4). Теорему Лагранжа можно использовать для приближенных вычислений: f (b)− f (a)= f ′ a +θ (b − a) (b − a), где 0 <θ <1. Положим θ = 12 ,

164

Лекция 16

тогда f (b)− f (a)≈ f ′ a + b

(b − a).

Погрешность

тем меньше, чем

ближе b к a .

Пример:

arctg1,1 = ?

b =1,1 ; a =1, 0 ;

b −a = 0,1; arctg1,1 ≈ arctg1+0,1 (arctg x)′ ,

x = 1,1+1,0

= 2,1 .

(arctg x)′ =

;

2,1 =

≈ 0,5 , arctg1,1 ≈

π +0, 05 .

1+ x2

2,1

16.1.3. Теорема Коши (обобщенная теорема о конечных разностях)

ТЕсли: 1) f (x),ϕ(x) непрерывны на [a,b], 2) на (a,b) существуют про-

изводные f ′(x),ϕ′(x), 3) ϕ′(x)≠ 0 x (a,b), то существует, по край-

ней мере, одна точка ξ (a,b) такая, что	f (b)− f (a)	=	f ′(ξ )	.
	ϕ(b)−ϕ(a)
			ϕ′(ξ )

Доказательство:

ϕ(b)≠ϕ(a), так как иначе, по теореме Ролля, ϕ′(x) обратилась бы в ноль, по крайней мере, в одной точке ξ (a,b).

Рассмотрим вспомогательную функцию:

F (x)= f (x)− f (a)−	f (b)− f (a)	ϕ(x)−ϕ(a) .
	ϕ(b)−ϕ(a)


Она удовлетворяет всем условиям теоремы Ролля, следовательно, суще-
ствует точка ξ (a,b) такая, что F′(ξ )= 0 ,
	f (b)− f (a)						f (b)− f (a)
F′(ξ )= f ′(ξ )−			ϕ′(ξ )= 0 , f ′(ξ )=					ϕ′(ξ ).
F′(ξ )= f ′(ξ )−	ϕ(b)−ϕ(a)		ϕ′(ξ )= 0 , f ′(ξ )=				ϕ(b)−ϕ(a)	ϕ′(ξ ).
Разделим на ϕ′(ξ ), ϕ′(ξ )≠ 0 , получим
		f (b)− f (a)			f ′(ξ )
				=		.
		ϕ(b)−ϕ(a)		=	ϕ′(ξ)	.

!Теорема Лагранжа является частным случаем теоремы Коши.

методами дифференциального исчисления.

Рассмотрим F (x)= ϕf ((xx)), где f (x) и ϕ(x) дифференцируемы в неко-

торой окрестности точки a , исключая, быть может, саму точку a . Если при
x → a	f	(x)		и ϕ(x) → 0		(∞), функция F (x) имеет в точке a неопределен-
ность	0		или		∞
ность	0		или		.
	0				∞

Вычислить lim F (x) поможет следующая теорема (правило Лопиталя).

x→a

ТПравило Лопиталя. Если: 1) f (x), ϕ(x) - непрерывны на [a,b]; 2) на (a,b) существуют f ′(x), ϕ′(x), причем ϕ′(x)≠ 0 ;

3) f (a)=ϕ(a)= 0 ; 4) существует предел lim

x→a

предел lim f (x), причем

x→a ϕ (x)

Доказательство: Возьмем на отрезке [a,b]

lim	f (x)	= lim	f ′(x)	.
	ϕ (x)
x→a		x→a	ϕ′(x)

точку x ≠ a .

f ′(x)

ϕ′(x) , то существует и

На отрезке [a, x] по теореме Коши

f (x)

− f (a)

f ′(ξ)

a <ξ < x ,

ξ -

ϕ(x)

−ϕ(a)

ϕ′(ξ)

промежуточная точка отрезка [a, x].

Но f (a)=ϕ(a)= 0 , значит,

f (x)

′(ξ )

. Если x → a ,то и ξ → a , сле-

ϕ(x)

ϕ′(ξ )

f (x)

довательно, lim

= lim

f ′(ξ )

= lim

f ′(x)

ϕ(x)

ϕ′(ξ )

ϕ′(x)

x→a

ξ→a

x→a

Более коротко это утверждение формулируют так: предел отношения двух бесконечно малых функций равен пределу отношения их производных, если последний существует.

! 1). Если рассматривается предел при x → ∞, ϕ(x)→ 0 , f (x)→ 0 , то утверждениеостостаетсясправесправедливым: :

			1
	f (x)		f
lim	f (x)	= lim	z	=
lim	ϕ(x)	= lim	1	=
x→∞	ϕ(x)	z→0	1
			ϕ
			z

x = 1z z → 0

= lim

z→0

	1		1
f ′		−
			z	2
z					= lim
			1
	1				z→0
ϕ′		−
			z	2
z

	1
f ′			f ′(x)
z		= lim	f ′(x)	.
		= lim		.
	1	x→∞	ϕ′(x)
ϕ′
z

166

Лекция 16

2). Если

f ′(a)=ϕ′(a)= 0 и

f ′(x), ϕ′(x) удовлетворяют условиям тео-

ремы,

то

можно

применять

правило

Лопиталя

f ′(x)

lim

f ′(x)

= lim

f ′′(x)

. Правило Лопиталя можно применять не-

ϕ′(x)

ϕ′′(x)

x→a ϕ′(x)

x→a

сколько раз.

3). Без доказательства приведем следующее утверждение:

(x)

∞

f ′(x)

lim

= lim

ϕ(x)

ϕ′(x)

x→a

∞

x→a

Предел отношения двух бесконечно больших функций равен пределу отношения их производных, если последний существует.

Применение правила Лопиталя для раскрытия неопределенностей

Пример:

lim sin 2x

= lim cos 2x 2

= 2 .

x→0

б)

lim

= lim

= ∞ .

x −sin x

1−cos x

sin x

x→0

Пример:

∞
	.
∞
a)	lim	ax	= lim	ax ln a			= ∞ .
a)	lim	x	= lim	1			= ∞ .
б)	x→∞	x	x→∞	1		(x +1)−2		= lim	1 = 0 .
б)	lim	x +1 = lim			12	(x +1)−2		= lim	1 = 0 .
							1

	x→∞		x	x→∞			1	x→∞ 2 x +1

Пример:

	0
		. f (x)→ 0 , ϕ (x)→ ∞ .
a) [0 ∞]=	0	. f (x)→ 0 , ϕ (x)→ ∞ .
	∞	x→a	x→a

	∞

lim f (x) ϕ (x)= lim

f (x)

= lim

ϕ (x)

∞

x→a

∞

ϕ (x)

f (x)

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

167

Пример:

ln x

∞

lim x

ln x =[0 ∞]= lim

= lim

= = lim

−

= 0

x→0

∞

x→0

−2

Пример:

00 , ∞0 , 1∞ . Применяется предварительное логарифмирование, откуда следует неопределенность [0 ∞].

Пример:

y = xx , x →0 . lim xx = ?
		x→0
Логарифмируем: ln y = x ln x .
Вычислим:								1
				ln x		∞		1
lim ln y = lim x ln x =[0 ∞]= lim				ln x		∞		x
					=		= lim	x		= 0 .
				1	=		= lim	1		= 0 .
x→0	x→0		x→0	1		∞	x→0	1
				x				−
				x				−	x2
limln y = 0 ,		ln lim y = 0 , lim y =1, lim xx =1.
x→0		x→0	x→0	x→0

16.1.5. Формула Тейлора

ТЕсли f (x) дифференцируема (n +1) раз в окрестности точки x0 , то для любого x из указанной окрестности справедлива формула Тейлора порядка n:

f (x) = f (x0 ) + f ′(x0 ) (x − x0 ) + f ′′(x0 ) (x − x0 )2 +

1! 2!

f ′′′(x0 )

(x − x

)3 +... +

f (n) (x0 )

(x − x

(x),

n+1

где

(x) =

f (n+1) (x +θ(x − x ))

(x − x )

n+1

; 0

<θ <1.

n+1

(n +1)!

Rn+1(x) называется остаточным членом в форме Лагранжа.

Доказательство: Обозначим

ϕ(x, x0 )= f (x0 )+ f ′1!(x0 )(x − x0 )+... + f (nn) (!x0 )(x − x0 )n ,

ϕ(x, x0 ) - многочлен n-го порядка (так называемый многочлен Тейло-

ра), Rn+1 (x)= f (x)−ϕ(x, x0 ).

168

Лекция 16

Покажем, что данная формула справедлива. Зафиксируем x из указанной окрестности, пусть x > x0 . На отрезке [x0 , x] рассмотрим вспомога-

тельную функцию:

Ф(t) = f (x)−ϕ (x, t)−	(x −t)n+1		Rn+1 (x), где t [x0 , x].
	(x − x	)n+1

	0

Поскольку Ф(x0 ) = Ф(x), Ф(t)удовлетворяет условиям теоремы Ролля и существует точка ξ (x0 , x), в которой Ф′(ξ ) = 0 .

Для вычисления Ф′(t) запишем ϕ(x,t ):

ϕ(x,t) = f (t) +

f ′(t)

(x −t) +

f ′′(t)

(x −t)2 +…+

f (n) (t)

(x −t)n .

Ф′(t) = −ϕt′(x, t)+ (n +1)

(x −t)n

Rn+1 (x).

(x − x )n+1

ϕt′(x, t) = f ′(t) +

f ′′(t) (x −t) −

f ′(t) +

f ′′′(t)

(x −t)2 −

−

f ′′(t)

2 (x −t) +... +

f (n+1) (t)

(x −t)n −

f (n) (t)

n (x − t)n−1

= f (n+n1!) (t)(x − t)n .

Следовательно,
−Ф′(t) =	f (n+1)	(t)	(x −t)	n	−(n +1)	(x −t)n	Rn+1 (x),
−Ф′(t) =	n!		(x −t)		−(n +1)	(x − x0 )n+1	Rn+1 (x),
	n!					(x − x0 )n+1
при t =ξ

Rn+1 (x)= f((nn++1)1(ξ)!)(x − x0 )n+1 .

! 1). Формула Тейлора порядка n позволяет представить функцию y = f (x) в виде суммы многочлена n–й степени и остаточного члена.

2). Полученная формула для Rn+1 (x) дает остаточный член в форме Лагранжа, но есть и другие формы остаточного члена, например, в форме Пеано: Rn+1 (x)= o((x − x0 )n ) - бесконечно малая более высокого порядка

малости по сравнению с (x − x0 )n .

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

169

Частные случаи формулы Тейлора

1). При x0 = 0 формула Тейлора называется формулой Маклорена:


f (x) = f (0)+	f ′(0)	x +		f ′′(0)	x2 +... +			f (n) (0)	xn + R	(x),
f (x) = f (0)+		x +			x2 +... +				xn + R	(x),
1!			2!					n!	n+1
1!			2!					n!
Rn+1 (x)=			f (n+1) (θ x)			xn+1	; 0 <θ <1.
Rn+1 (x)=						xn+1	; 0 <θ <1.
			(n +1)!

2). Рассмотрим f (x)= c0 + c1x1 + c2 x2 +... + cn xn - многочлен порядка n .

Поскольку x f (n+1) (x)= 0 , то x		Rn+1 (x)= 0 и
f (x)= f (x0 )+	f ′(x0 )	(x − x0 )+... +	f (n)	(x − x0 )	n	.
	1!		n!

Вывод: по формуле Тейлора любой многочлен порядка n можно представить в виде многочлена по степеням (x − x0 ).

Пример:

Многочлен 2x3 −3x2 + 5x +1 разложить по степеням (x +1) . Решение:

f (x) = 2x3 −3x2 +5x +1; x0 = −1 ; f (−1) = −9 .

Ищем коэффициенты формулы Тейлора:

f	′	= 6x	2	− 6x + 5 → f			′	=17;
f	(x)	= 6x		− 6x + 5 → f			(−1)	=17;
f	′′	=12x		− 6	→ f		′′	= −18;
f	(x)	=12x		− 6	→ f		(−1)	= −18;
f	′′′				→ f	′′′		=12;
f	(x) =12				→ f		(−1)	=12;
f IV (x) = 0

f (n) (x) = 0;
f (x) = −9 +				17 (x +1) −18 (x +1)2 +					12	(x +1)3 .
				1!		2!			3!
Учитывая, что 1!= 1; 2!= 1 2 ;								3!=1 2 3 , получим ответ:

2x3 −3x2 +5x +1 = −9 +17(x +1) −9(x +1)2 + 2(x +1)3 .

170 Лекция 16

Разложение по формуле Маклорена некоторых элементарных функций

f (x) = ex ,

f (0)=1,

f ′(x) = ex ,

f ′(0) =1,

f ′′(x) = ex ,

f ′′(0) =1,

f (n) (x) = ex ,

f (n) (0) =1.

ex =1+

+... +

+ R

(x), R

(x)=

eθx

xn+1 .

(n +1)!

1! 2!

n+1

f (x)= sin x ;

(0)= 0 ,

f ′(x)= cos x = sin

(x + π2 )

;

f ′(0)=1,

f ′′(x)= −sin x = sin (x + 2π2 );

f ′′(0)= 0,

f ′′′(x)= −cos x = sin (x +3π2 );

f ′′′(0)= −1,

……………………………………………..,

f (n) (x)= sin (x + nπ2 ),

(n)

(

n – нечетное,

(0)= sin

n π

n−1

n - четное

2 )

(−1) 2

sin x = x −

+... +(−1)n

x2n+1

+ R

(x).

(2n +1)!

2n+2

!Нечетная функция sin x разложена по нечетным степеням x .

f (x)= cos x ,

f (0)=1,

f (n) (x)= cos(x + n π2 ),

(n)

(

n – четное,

(0)= cos

n π

n - нечетное

2 )

(−1)2

cos x =1 −

−... + (−1)n

x2n

+ R

(x)

(2n)!

2n+1

Четная функция cos x разложена по четным степеням x .

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

171

4.f (x) = ln (1 + x)

′

(x)= 1

+ x ,

′′

(x)= −(1+ x)2

′′′

(x)= (1+ x)3

f (n) (x)= (−1)n−1 (n −1)!, (1+ x)n

f (0) = 0 ,

f ′(0)=1,

f ′′(0)= −1,

f ′′′(0)=1 2 ,

f (n) (0)= (−1)n−1 (n −1)!.

ln (1+ x)= x −	x2	+	x3	−... + (−1)n−1	xn	+ R	(x).
					n
2		3				n+1

5.f (x)= (1 + x)α , где α -любое вещественное число.


(1	+ x)α =1+α x +		α(α −1)		x2 +... +	α(α −1)...(α − n +1)		xn + R	(x).

	2!						n!	n+1

Частный случай α = n :
(1	+ x)n =1+ nx +	n(n −1)		x2	+... + n!xn		- формула бинома Ньютона.

	2!				n!

Формулы Маклорена для элементарных функций:

xn+1

θ x

1. e

=1 + x +

+... +

; 0

θ <1.

(n +1)!

x2n+1

x2n+2

2n + 2

2. sin x = x −

−... +

(−1)

sin(θx +

π); 0

<θ <1.

(2n +1)!

(2n + 2)!

3. cos x =1−

x2n

x2n+1

cos(θx +

2n +1

π); 0 <θ <1.

−... +

(−1)

(2n)!

(2n +1)!

4. ln(1 + x) = x −

−

+... + (−1)n−1

(−1)n xn+1

; 0 <θ <1.

(n +1)! (1 +θ x)n

172

Лекция 16

Оценка остаточного члена

Пусть f (x)

такова, что n и x из окрестности точки x0

f (n) (x)

≤ M .

Рассмотрим остаток: R (x)=

f (n+1)(ξ)

(x − x )n+1 .

n+1

(n +1)!

(x)

f (n+1) (ξ)

x − x

n+1 ≤ M

x − x0

n+1

x − x

при n → ∞

n+1

(n +1)!

x − x

n+1

→ 0 и остаточный член может быть сделан сколь угодно малым пу-

(n +1

тем увеличения n .

Итак, если

f (x) обладает указанным выше свойством, то формулу Тей-

лора можно использовать для приближенных вычислений с любой наперед заданной точностью.

Приложения формул Тейлора и Маклорена

1). Для вычисления приближенных значений функций:

f (x)≈ f (x0 )+ f ′1!(x0 )(x − x0 )+... + f (nn) (!x0 )(x − x0 )n .

Погрешность (ошибка) вычисления находится по оценке остаточного члена. Rn+1 (x) ≤ε , где ε - погрешность.

Пример:

Вычислить e с точностью ε =10−3 .

Рассмотрим

ex , x =1, x

= 0 .

+ Rn+1 (1) , Rn+1 (1)=

eθ

e =1+

+...+

, 0 <θ <1 .

(n +1)!

Rn+1 (1)

, e < 3

≤ε .

(n +1)!

n ,

≤ 0,001:

Найдем

наименьшее

удовлетворяющее условию

(n +1)!

n = 6 .

e =1+1!1 + 2!1 +... + 6!1 = 1957720 = 2,714 .

Основные теоремы анализа. Правило Лопиталя – Бернулли. Формула Тейлора

173

2). Для вычисления пределов функций:

Пример:

sin x − x

{x −

+...}− x

−

+...

lim

= lim

= −

x→0

В результате изучения материала, изложенного в этих лекциях, студент должен знать:

теорему Ролля (о нуле производной) и теорему Лагранжа (о конечных приращениях);

правило Лопиталя – Бернулли раскрытия неопределенностей и способы его применения к неопределенностям вида

0		∞		0		0	∞	;
	,		, [0 ∞], 0		, ∞		, 1	;
0		∞

вид многочленов Тейлора для основных элементарных функций.

Часть 2

Лекции 1 - 2 ИССЛЕДОВАНИЕ ФУНКЦИЙ И ПОСТРОЕНИЕ ГРАФИКОВ

Графическое описание поведения функции очень полезно, так как наглядность графика делает его незаменимым вспомогательным средством исследования свойств функции. Графики функций, получающиеся из графиков основных элементарных функций с помощью геометрических преобразований, очевидны. Графики сложных функций не могут быть построены без использования дифференциального исчисления. В данных лекциях приводится общая схема исследования функций и ее теоретическое обоснование. Последовательное применение этой схемы позволяет построить график любой сколь угодно сложной функции, возникающей в технических приложениях.

1.1.Исследование функций без привлечения производных

1.1.1.Точки разрыва

1.1.2.Асимптоты графика функции

1.1.3.Вертикальные асимптоты

1.1.4.Горизонтальные асимптоты

1.1.5.Наклонные асимптоты

1.2.Исследование функций с помощью первой производной

1.2.1.Монотонность функции

1.2.2.Локальный экстремум функции

1.2.3.Необходимые условия экстремума

1.2.4.Достаточные условия экстремума

1.2.5.Правило отыскания экстремумов функции

2.1.Исследование функций с помощью второй производной

2.1.1.Исследование функций на максимум и минимум

спомощью второй производной

2.1.2.Направление выпуклости и точки перегиба кривой

2.2.Общая схема исследования функции и построения графика

2.3.Примеры исследования функций

1.1.Исследование функций без привлечения производных

Построение графика функции y = f (x) применяется, как правило, для

возможно более точной характеристики хода изменения функции, точность расположения отдельных точек графика обычно представляет меньший интерес.

176

Лекции 1 - 2

1.1.1. Точки разрыва

Функция y = f (x) называется непрерывной в точке

x0 ,

если функция

определена в

точке

существуют

пределы

lim f (x) =

x→x0 −0

= lim

f (x) = lim f (x), и при этом lim f (x) = f (x0 ).

x→x0 +0

x→x0

Точка x0 , в которой функция y = f (x) обладает свойством непрерывно-

сти, называется точкой непрерывности функции, в противоположном

случае точка x0

называется точкой разрыва функции.

Если

односторонние

пределы

существуют,

причем

lim f (x) =

f (x) и функция y = f (x) не определена в точке x0

x→x0 −0

= lim

или нарушено

x→x0 +0

то точка x0

условие lim f (x) = f (x0 ) ,

называется точкой устранимого

x→x0

разрыва.

Пример:

Исследовать поведение функции

f (x)= sinx

в точке x0 = 0 .

В точке x0 = 0 функция не определена, т.е. x0

= 0 - точка разрыва.

В теории пределов был доказан 1-й замечательный предел lim sinx =1,

lim sinx

= lim sinx =1 и x0 = 0

x→0 x

следовательно,

является точкой устрани-

мого разрыва.

x→+0

x→−0

= 0 , доопределим ее, по-

Чтобы функция стала непрерывной в точке

ложив

f (0)= lim f

(x)=1 (так называемое доопределение по непрерыв-

x→0

sinx

, x ≠ 0,

ности).

будет не-

Новая, доопределенная функция f (x)= x

x = 0

прерывна на новой области определения – всей числовой оси.

О	Если	односторонние	пределы	существуют,	причем
	lim	f (x) ≠ lim f (x), то точка х0 называется точкой разрыва 1-го ро-
	lim
	x→x0 −0	x→x0 +0

да.

Пример:

Исследовать поведение функции y = xx в точке x0 = 0 .

В точке x0 = 0 функция не определена, так как знаменатель равен нулю, т.е. x0 = 0 - точка разрыва.

Исследование функций и построение графиков

177

По определению модуля

если

x ≥ 0;

−x,

если

x < 0.

Левый предел: lim =

= lim

−x

= lim (−1)= −1 .

x→−0

Правый предел: lim =

= lim

= lim 1 =1 .

x→+0

Односторонние пределы конечны, но не равны друг другу, следовательно, точка x0 = 0 является точкой разрыва 1-го рода.

ОЕсли хотя бы один из односторонних пределов не существует или бесконечен, то точка x0 называется точкой разрыва 2-го рода.

Пример:

Определить точки разрыва функции f (x)= e x и исследовать характер

разрыва.
Решение:			x0 = 0 . Вычислим левый предел, учитывая,
Функция разрывна в точке			x0 = 0 . Вычислим левый предел, учитывая,
		1	1
что lim ex = 0 . Так как lim		1	= −∞, lim ex = 0 .
x→−∞	x→−0	x	x→−0		1 = +∞,
Вычислим правый предел, учитывая, что lim ex = ∞. Так как lim					1 = +∞,
1			x→+∞	x→+0	x
1				x0 = 0 является точкой
lim ex = ∞ . Правый предел бесконечен, точка				x0 = 0 является точкой
x→−0

разрыва 2-го рода.

1.1.2. Асимптоты графика функции

О	Если расстояние от точки, лежащей на кривой, до некоторой прямой
	стремится к нулю при неограниченном удалении этой точки от начала

	координат, то эта прямая называется асимптотой кривой. Асимптоты
	могут быть вертикальными, горизонтальными и наклонными.
1.1.3. Вертикальные асимптоты
	Прямая x = x0 является вертикальной асимптотой графика функции
О
	y = f (x),	если хотя бы одно из предельных значений lim f (x) или

	lim f (x)	x→x0 −0
		равно +∞ или−∞.
	x→x0 +0

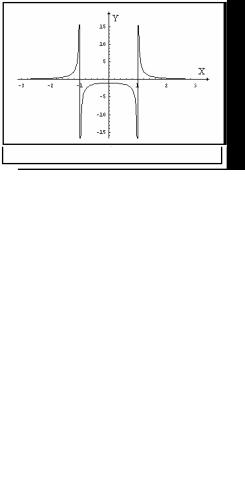
178	Лекции 1 - 2

Так, график функции y = 1x имеет вер-

тикальную асимптоту x = 0 , поскольку

lim	1	= −∞ ,	lim	1	= +∞.
x→0−0	x		x→0+0	x

Для разыскания вертикальных асимптот кривой y = f (x)

1)находим на оси Ox точки разрыва функции f (x);

2)выделяем те из них, в которых хотя бы один из пределов функции f (x) (слева или

справа) равен +∞ или −∞. Пусть это будут точки x1, x2 ,..., xm , тогда прямые

x = x1

x = x2 ,…, x = xm будут вертикальными асимптотами графика функции

y = f

(x).

Например,

для кривой

y =

вер-

x2 −1

тикальными

асимптотами

будут

прямые

x = −1

x =1.

Вертикальная

прямая

x = x0

может оказаться

асимптотой

гра-

фика функции

y = f (x)

и в том случае,

когда точка

является концом интерва-

ла,

в котором определена функция f (x).

Это будет тогда, когда

x0 - левый конец

интервала

lim

f (x)= +∞

или

-∞, либо когда x0 - правый конец интерва-

x→x0 +0

ла

lim f

(x)= +∞

или

-∞. Например, функция y = ln x определена в ин-

x→x0

−0

тервале 0 < x < +∞,

и для нее lim ln x = −∞, так что прямая x = 0 (ось Oy )

x→0+0

является вертикальной асимптотой графика функции y = ln x .

1.1.4. Горизонтальные асимптоты

Прямая y = b называется правой горизонтальной асимптотой графика

функции y = f (x), если lim f (x)= b .

y = b

x→+∞

Прямая

называется левой горизонтальной асимптотой графика

функции y = f (x), если lim f (x)= b .

x→−∞

Функция f (x) в этом случае представима в виде f (x)= b +α(x), где

lim α (x)= 0 .

x→±∞

Исследование функций и построение графиков

179

Возможны следующие ситуации:

1)не существует ни левой, ни правой горизонтальной асимптоты ( f (x) = x2 );

2)существует левая горизонтальная асимптота и не

существует правой ( f (x)= ex , lim f (x)= 0 , y = 0 - ле-

x→−∞

вая горизонтальная асимптота);

3) существует правая горизонтальная асимптота и не

существует левой ( f (x) = e−x , lim f (x) = 0 , y = 0 -

x→+∞

правая горизонтальная асимптота);

4) обе горизонтальные асимптоты существуют, но не

совпадают ( f (x) = arctgx , lim f	(x)= −	π	,	y = −			π	- ле-
x→−∞		2			π		2		π
вая горизонтальная асимптота;	lim f	(x)=			π	,	y	=	π	-
	x→+∞				2				2
	x→+∞				2				2

правая горизонтальная асимптота;

5) обе горизонтальные асимптоты существуют и сов-

падают ( f (x)=	1	, lim f (x)= lim f (x)= 0 , y = 0 - урав-
	x	x→−∞	x→+∞

нение обеих горизонтальных асимптот).

1.1.5. Наклонные асимптоты

Прямая y = kx + b

называется правой наклонной асимптотой графика

функции y = f

(

)

x→+∞

(

)

− kx −b

)

= 0 .

, если lim

В этом случае функция

f (x)

представима в виде f (x)= kx + b +α (x),

где lim α (x)= 0.

x→+∞

Существование асимптоты y = kx + b у кривой y = f (x) при x → +∞ означает, что при x → +∞ функция y = f (x) ведет себя «почти как линейная

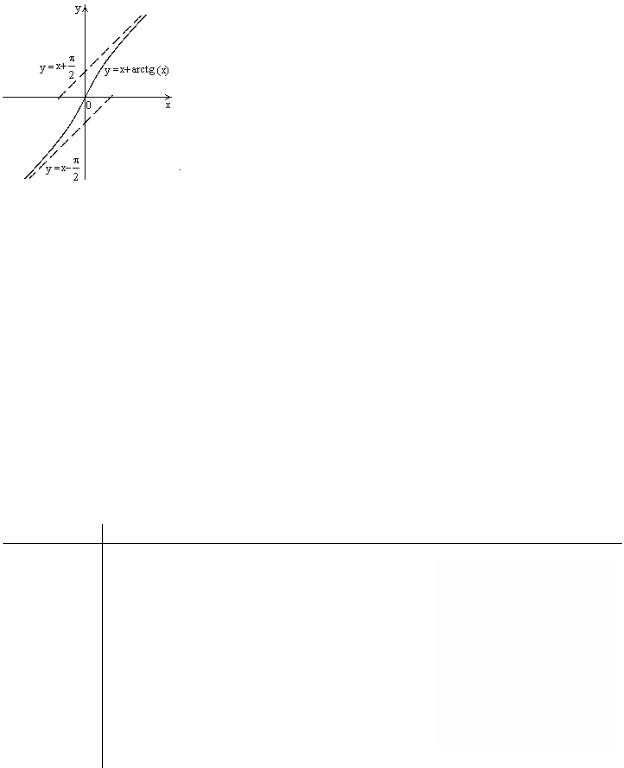
180	Лекции 1 - 2

функция», т.е. отличается от линейной функции y = kx + b на бесконечно малую функцию при x → +∞.

Т Для того чтобы график функции y = f (x) имел при x → +∞ наклонную асимптоту y = kx + b , необходимо и достаточно, чтобы существовали два

предела:

(x)

1) lim

= k ; 2)

lim

f (x)− kx = b .

x→+∞

Доказательство:

Необходимость.

Пусть

график

функции

y = f (x)

при

x → +∞

имеет

асимптоту

y = kx + b ,

т.е.

для

f (x)

справедливо

f (x)= kx + b +α (x), α(x)→ 0 при x → +∞ .

f (x)

α (x)

Тогда lim

= lim

k +

= k ,

x→+∞

lim f (x)

− kx = lim b +α (x) = b.

x→+∞

Достаточность.

Пусть существуют оба предела k

и b . Существование

предела для b позволяет утверждать, что разность

f (x)− kx −b является

бесконечно малой функцией при x → +∞ . Обозначив эту разность через α (x), получим f (x)= kx + b +α (x), где α(x)→ 0 при x → +∞ . Это означает, что график функции y = f (x) имеет наклонную асимптоту y = kx + b . Аналогично исследуется случай x → −∞.

Пример:

Найти асимптоты графика функции y =x+arctgx .

lim	x +arctg x		= k+	= lim		x +arctg x	= k− =1,
						x
x→+∞		x		π	x→−∞
b+ = lim		(arctg x)=			,
	x→+∞			2	π ,
b− = lim		(arctg x)= −				график имеет две
	x→−∞				2

несовпадающие наклонные асимптоты: ле-

вую y = x − π2 и правую y = x + π2 .

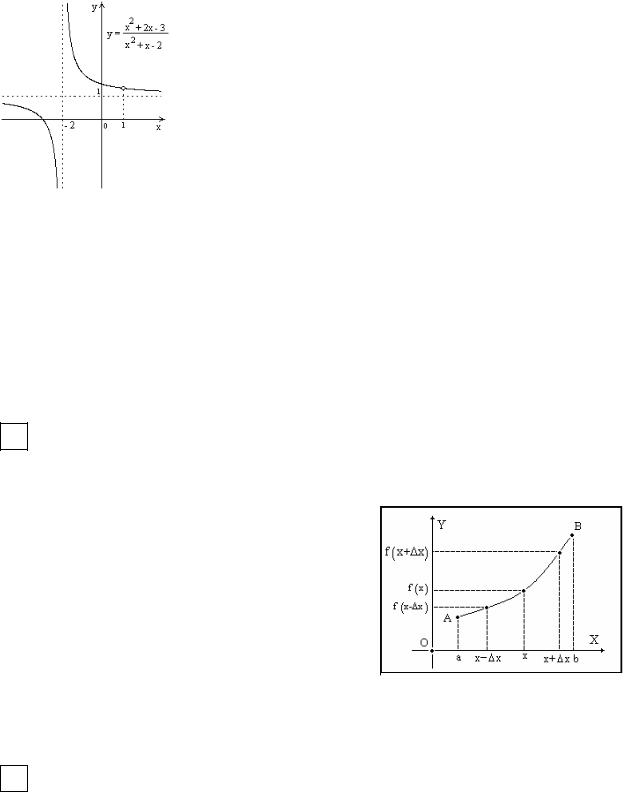
Исследование функций и построение графиков

181

Пример:

Построить график функции

y =

+ 2x −3

+ x − 2

без использования производной.

Решение:

Преобразуем выражение:

x2 + 2x −3

(x −1)(x + 3)

+ 2x −3

x +3

x2 + x − 2

(x −1)(x + 2)

+ x −2

x + 2

( x ≠1),

x + 3

= 1 +( x + 2 )

x + 2

x +

x + 2

т.е. y =

+1 , ( x ≠1). График этой функ-

x + 2

1 на две единицы влево, на од-

ции получается смещением графика y =

ну единицу вверх и выкалыванием точки графика с абсциссой x =1.

1.2. Исследование функций с помощью первой производной.

1.2.1. Монотонность функции

О Пусть функция f (x) определена на отрезке [a,b]. Если для любых x1, x2 [a,b] из условия x1 < x2 следует неравенство:

1)f (x1 )≤ f (x2 ), то функция f (x)

неубывающая на [a,b];

2)f (x1 )< f (x2 ), то функция f (x)

возрастающая на [a,b];

3)f (x1 )≥ f (x2 ), то функция f (x)

невозрастающая на [a,b];

4)f (x1 )> f (x2 ), то функция f (x)

убывающая на [a,b].

Функции всех этих типов носят общее название монотонных; возрастающие и убывающие функции называются строго монотонными.

ТПусть функция f (x): 1) непрерывна на отрезке [a,b]; 2) имеет производную f '(x) по крайней мере на интервале (a,b).

Для того чтобы функция f (x) на отрезке [a,b] была неубывающей (невозрастающей), необходимо и достаточно выполнение условия f '(x)≥ 0

182 Лекции 1 - 2

( f '(x) ≤ 0 ) для всех точек x из интервала (a,b).

Доказательство:

Необходимость. Пусть функция f (x) является неубывающей

на отрезке [a,b]. Докажем, что на интервале (a,b) производная f '(x) ≥ 0 . Возьмем точки x и x + ∆x в интервале (a,b). Так как по условию f (x) неубывающая, то при любом ∆x (положительном или отрицательном) знак ∆x и f (x + ∆x)− f (x) один и тот же, и поэтому

f (x + ∆x)− f (x) ≥ 0 .

∆x

Учитывая, что по условию в каждой точке x интервала (a,b) существует производная f '(x), из последнего равенства получим

f '(x)= lim	f (x +∆x)− f (x)	≥ 0 .

∆x→0	∆x
Итак, в любой точке интервала (a,b) имеем f '(x)≥ 0 .
Достаточность. Пусть f '(x)≥ 0	на интервале (a,b). Докажем, что функ-

ция f (x) - неубывающая на отрезке [a,b]. Действительно, пусть x1 < x2 - любые две точки отрезка [a,b].

По теореме Лагранжа f (x2 )− f (x1 )= f '(ξ )(x2 − x1 ), где x1 <ξ < x2 . Так
как f '(x)≥ 0 в каждой точке x интервала (a,b), то и f '(ξ )≥ 0 . Кроме
того x2 > x1 . Поэтому f (x2 )≥ f (x1 ). Итак, из неравенства x1 < x2 следует
неравенство f (x1 )≤ f (x2 ), а это и означает, что на отрезке [a,b]	функ-
ция f (x) неубывающая.
Таким образом, интервалы знакопостоянства производной f '(x)	явля-

ются интервалами монотонности функции	f (x).
Справедливо следующее утверждение (достаточное условие возрастания
функции): если f '(x)> 0 на интервале (a,b), то		f (x) на отрезке [a,b] воз-
растает. Однако если f (x) возрастает на	[a,b],	то отсюда не следует, что
f '(x)> 0 всюду на интервале (a,b).

Пример:

Функция f (x) = x3 возрастает на отрезке [−1,1], однако ее производная f '(x)= 3x2 обращается в нуль в точке x = 0 .

Рассмотрим возрастание или убывание функции в точке.

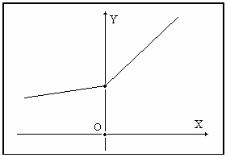
Исследование функций и построение графиков

183


	Функция f (x) называется возрастающей в точке x = x0 , если сущест-
О
	вует	такая окрестность (x0 −δ, x0 +δ ) точки x0 ,		в которой для	всех

	x < x0	имеем f (x) < f (x0 ), а для всех x > x0 верно		f (x) > f (x0 ).
	Функция f (x) называется убывающей в точке x = x0 , если существует
	такая окрестность (x0 −δ, x0 +δ ) точки x0 ,		в которой для всех		x < x0
	имеем f (x) > f (x0 ), а для всех x > x0 верно		f (x) < f (x0 ).

Следующая теорема выражает достаточные условия возрастания и убывания функции в точке.

f (x)

в точке

x = x0

имеет производную

f '(x). Если

Пусть функция

f '(x0 ) > 0 , то функция

f (x)

в точке

возрастает; если

f '(x0 ) < 0 , то

f (x) в точке x0 убывает.

Доказательство:

Пусть f '(x0 ) > 0 . Это означает, что

lim

f (x0

+ ∆x)− f (x0 )

> 0 .

∆x

∆x→0

δ > 0 , что

Но тогда существует такое

для всех ∆x , удовлетворяющих усло-

вию 0 <

∆x

<δ , верно неравенство

(x0 + ∆x)− f (x0 )

> 0 .

∆x

<δ величины f (x0 + ∆x)− f (x0 ) и ∆x

∆x

Отсюда следует, что при 0 <

имеют один и тот же знак: если ∆x <0,

то и

f (x0 + ∆x)− f (x0 )<0,

т.е.

f (x0 + ∆x)< f (x0 ); если же

∆x >0,

то и

f (x0 + ∆x)− f (x0 )>0,

т.е.

f (x0 + ∆x)> f (x0 ). Согласно определению, это и означает, что функция

f (x) в точке x0 возрастает.

f '(x0 )< 0 , то функция f (x) в

Аналогично можно доказать, что если

точке x0 убывает.

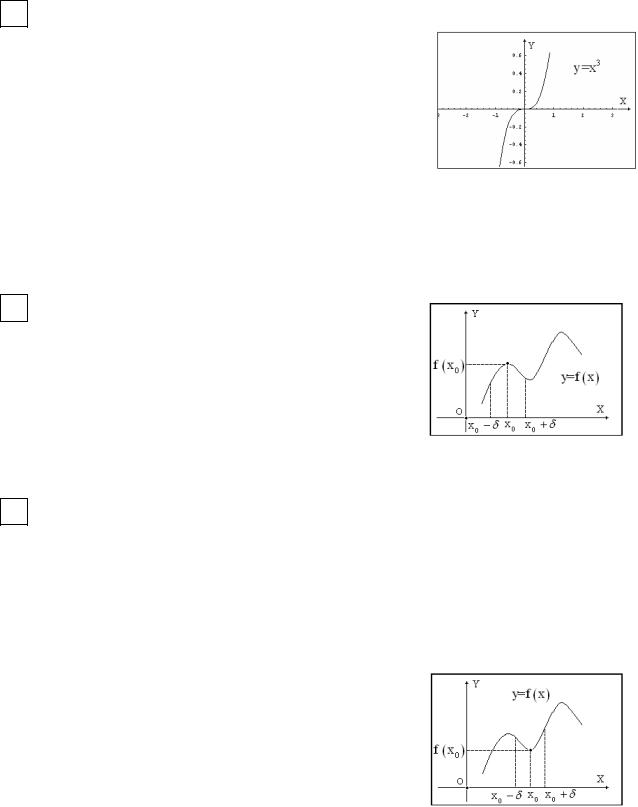
184	Лекции 1 - 2

!Теорема дает достаточные, но не необходимые условия возрастания и убывания функции в точке. Так, функция, гра-

фик которой приведен на рисунке, возрастает в точке x = 0 , но в этой точке производная функ-

ции не существует.

Функция f (x)= x3 возрастает в точке x = 0 , но

ее производная f '(x) в точке x = 0 обращается

внуль.

1.2.2.Локальный экстремум функции

ОПусть функция f (x) определена в некото-

рой окрестности точки x0 , включая и саму точку x0 . Точка x0 называется точкой ло-

кального максимума (минимума) функ-

ции f (x), если существует такое δ > 0 , что

для всех x из интервала (x0 −δ, x0 +δ )

верно неравенство:

∆f = f (x)− f (x0 ) ≤ 0 ( ∆f = f (x)− f (x0 ) ≥ 0 ).

ОЗначение функции f (x) в точке максимума называется локальным

максимумом, а значение функции в точке минимума - локальным минимумом данной функции.

Локальные максимум и минимум называются локальными экстрему-

мами.

Эти определения означают, что f (x0 ) - локальный максимум функции f (x), если существует такой интервал (x0 −δ, x0 +δ ), в котором f (x0 ) является наибольшим значением функции f (x), и f (x0 ) - локальный минимум функции f (x), если существует интервал

(x0 −δ, x0 +δ ), в котором f (x0 ) является наименьшим значением функции на этом интервале.

Термин локальный (местный) обусловлен тем, что введенное понятие экстремума связано с окрестностью данной точки в области определения функции, а не со всей этой областью. В дальнейшем слово «локальный» бу-

Исследование функций и построение графиков

185

дем для краткости опускать. Мы будем рассматривать лишь точки строгого максимума и минимума.

Точка x0 называется точкой строгого максимума (минимума) функции

f (x), если существует δ > 0 такое, что для всех

x , удовлетворяющих

условию 0 <

x − x0

<δ , верно строгое неравенство

f (x)− f (x0 )< 0 (со-

ответственно

f (x)

− f (x0 )> 0 ). В приведенном определении не предпо-

лагается непрерывности функции f (x) в точке x0 .

Пример:

x ≠ 0,

y = x

x = 0,

В точке 0 - максимум, хотя в ней нет не-

прерывности функции.

1.2.3. Необходимые условия экстремума


		f (x)	может иметь экстремум только в тех точках, в которых
Т	Функция
	ее производная		f '(x)		либо равна нулю, либо не существует.

	Доказательство:			x0 функция		f (x) имеет
	Пусть в точке
	производную и			f '(x0 )≠ 0 . Пусть для оп-
	ределенности		f '(x0 )> 0 . Тогда функция
	f (x) в точке x0			будет возрастающей. По-
	этому найдется такое δ > 0 , что для всех
	x из интервала			(x0 −δ, x0 )		верно нера-
	венство	f (x)< f (x0 ), а для всех x из ин-
	тервала	(x0 , x0 +δ )			верно	неравенство

f (x)> f (x0 ).

Из этого следует, что не существует окрестности точки x0 , в которой величина f (x0 ) была бы наибольшим или наименьшим значением функции f (x), и поэтому точка x0 не будет ни точкой максимума, ни точкой минимума функции f (x). Аналогичными рассуждениями придем к тому же выводу при f '(x0 )< 0 .

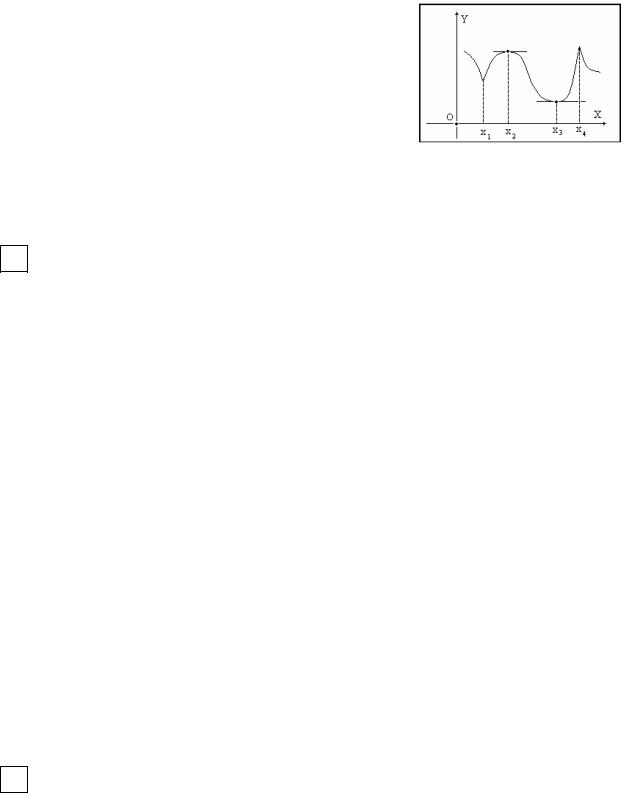
186	Лекции 1 - 2

Итак, если в точке x0 существует производная f '(x0 ) ≠ 0 , то в точке x0 не может быть ни максимума, ни минимума функции f (x). Следовательно, экстремум функции f (x) мо-

жет быть только в такой точке, в которой производная f '(x) либо равна нулю, либо не су-

ществует, что показано на рисунке.

Функция y = f (x) имеет экстремумы в точках x1, x2 , x3 , x4 ; при этом в точках x1 и x4 производная f '(x) не существует, а в точках x2 и x3 она равна нулю.

ОТочки, в которых выполняется необходимое условие экстремума для функции f (x), называются критическими точками этой функции. Они определяются как корни уравнения f '(x) = 0 и как точки, где f '(x) не существует (в частности, где f '(x) - бесконечно большая функция). Корни уравнения f '(x)= 0 называют стационарными точками функции f (x): скорость изменения f (x) в такой точке равна нулю.

Утверждение, обратное к теореме, неверно: не в каждой своей критической точке функция f (x) обязательно имеет максимум или минимум.

Например, для функции f (x)= x3 f	'(0)= 0 , поэтому точка x = 0 явля-
ется критической для данной функции. Но функция		f (x)= x3	в точке x = 0
экстремума не имеет: f (0)= 0 , для x < 0	f (x)< 0 ,	для x > 0	f (x)> 0 , так

что в	точке	x = 0	данная
	1
xsin		, x ≠ 0,	в точке
f (x) =	x		в точке

0, x = 0

экстремум отсутствует.

функция возрастает. Для функции

x = 0 производная не существует, однако

1.2.4. Достаточные условия экстремума

ТПусть x = x0 – критическая точка для функции f (x) и функция f (x)

непрерывна в точке x0 .

Пусть существует такое δ > 0 , что для всех x из интервала (x0 −δ, x0 )

производная f '(x)> 0, а для всех x из интервала (x0 , x0 +δ ) f '(x)< 0 , то есть при переходе x через точку x0 производная f '(x) меняет знак с плюса на минус. Тогда в точке x0 функция f (x) имеет максимум.

Исследование функций и построение графиков			187
Доказательство:
Так как по условию f '(x) > 0		в	интервале
(x0 −δ, x0 ), то на отрезке	[x0 −δ, x0 ]		функция
f (x) возрастает; так как	f '(x) < 0	в интервале
(x0 , x0 +δ ), то на отрезке	[x0 , x0 +δ ]		функция

f (x) убывает. Следовательно, f	(x0 ) есть наи-
большее значение функции f (x)	в окрестности (x0 −δ, x0 +δ ) точки x0 , а

это означает, что f (x0 ) есть локальный максимум функции f (x).

ТПусть x = x0 – критическая точка для функции f (x) и функция f (x) непрерывна в точке x0 .

Пусть существует такое δ > 0 , что для всех x из интервала (x0 −δ, x0 ) производная f '(x)< 0 , а для всех x из интервала (x0 , x0 +δ ) имеем f '(x)> 0, то есть при переходе x через точку x0 производная f '(x) меняет знак с минуса на плюс. Тогда в точке x0 функция f (x) имеет минимум.

1.2.5. Правило отыскания экстремумов функции

Чтобы найти точки максимума и минимума функции f (x), надо:

1). Найти производную f '(x), приравнять ее к нулю и решить полученное уравнение f '(x)= 0.

2). Найти точки, в которых производная f '(x) не существует. Эти точки и корни уравнения f '(x)= 0 будут критическими точками для функции

f (x).
3). Исследовать знак производной			f '(x) слева и справа от каждой критиче-
ской точки. Если при переходе x через критическую точку x0 произ-
водная f '(x) меняет знак с плюса на минус, то в точке x0				функция
f (x)	имеет максимум; если знак f '(x) меняется с минуса на плюс, то в
точке	x0 функция	f (x) имеет минимум. Если при переходе		x через
критическую точку		x0 знак	f '(x) не меняется, в точке x0	функция
f (x)	не имеет ни максимума, ни минимума.

188					Лекции 1 - 2
				Экстремум
	f ′(x0 − ∆x)	f ′ (x0 )	f ′(x0 + ∆x)	Экстремум
				нет
	> 0	0, ± ∞,	> 0
	> 0	0, ± ∞,	> 0
				max
	> 0	0, ± ∞,	< 0
	> 0	0, ± ∞,	< 0
				min
	< 0	0, ± ∞,	> 0
	< 0	0, ± ∞,	> 0
				нет
	< 0	0, ± ∞,	< 0
	< 0	0, ± ∞,	< 0

2.1. Исследование функций с помощью второй производной

2.1.1. Исследование функций на максимум и минимум

с помощью второй производной

ТПусть в точке x0 функция f (x) имеет первую и вторую производные, причем f '(x0 )= 0 , а f ''(x0 )≠ 0 . Тогда в точке x0 данная функция f (x) имеет максимум, если f ''(x0 )< 0 , и минимум, если f ''(x0 )> 0 .

Доказательство:

Точка x0 является критической точкой для данной функции f (x), так как f '(x0 )= 0 . Пусть f ''(x0 )< 0 . Из этого следует, что в точке x0 первая

производная	f '(x) убывает, то есть		существует такая окрестность
(x0 −δ, x0 +δ ) точки x0 , что для всех x			из интервала (x0 −δ, x0 ) верно
неравенство	f '(x)> f '(x0 )= 0 ,	а для всех x из интервала		(x0 , x0 +δ )
верно f '(x)< f '(x0 )= 0 .
Таким образом, при переходе x		через критическую точку x0		производ-

ная f '(x) меняет свой знак с плюса на минус. Следовательно, функция f (x) в точке x0 имеет максимум.

Подобными же рассуждениями доказывается, что если в критической
точке x0 вторая производная		f ''(x0 )> 0 , то функция f		(x) в точке x0
имеет минимум.

	f ′(x0 )	f ′′(x0 )	Экстремум
	0	< 0	max
	0	> 0	min
	0	0

Исследование функций и построение графиков

189

2.1.2. Направление выпуклости и точки перегиба кривой

Пусть кривая задана уравнением y = f (x) и пусть функция f (x) в точке x0 имеет конечную производную f '(x0 ), то есть в точке M 0 (x0 , f (x0 )) существует касательная к данной кривой, не параллельная оси Oy .

О	Если существует	такая	окрестность
	(x0 −δ, x0 +δ ) точки	x0 ,	что все точки

данной кривой, абсциссы которых содержатся в этой окрестности, расположены выше касательной к кривой в точке M0 ,

то говорят, что выпуклость данной кри-

вой в точке M0 направлена вниз.

Если все точки кривой с абсциссами из некоторой окрестности точки x0 находят-

ся ниже касательной к этой кривой в точ-

ке M 0 , то говорят, что выпуклость данной кривой в данной точке на-

правлена вверх.

ОБудем говорить, что график функции y = f (x), дифференцируемой на интервале (a,b), имеет на этом интервале выпуклость, направленную вверх (вниз), если график этой функции в пределах интервала (a,b) ле-

жит не выше ( не ниже) любой своей касательной. О графике, выпуклом вверх, часто говорят как о просто выпуклом, график, выпуклый вниз, называется вогнутым.

ТЕсли во всех точках интервала (a;b) функция f (x) имеет отрицатель-

ную вторую производную ( x (a;b) f ''(x)< 0 ), то график функции в этом интервале выпуклый вверх. Если x (a;b) f ''(x)> 0 - график

выпуклый вниз.

О Точка М0 (x0 , f (x0 )) называется точкой перегиба кривой y = f (x), если:

1) в точке x0 существует касательная;

2) существует такая окрестность

(x0 −δ, x0 +δ ) точки x0 , что для x < x0 из

190	Лекции 1 - 2

этой окрестности выпуклость кривой направлена в одну сторону, а при

x> x0 - в противоположную.

ТТочка М0 (x0 , f (x0 )) может быть точкой перегиба кривой y = f (x), только если f ''(x0 )= 0 (или f ''(x0 ) не существует).

Это условие не	является достаточным.	Так, например, для функции
f (x)= x4 имеем	f ''(x)=12x2 и f ''(0)= 0	, но точка O(0,0) не является

точкой перегиба кривой y = x4 : в этой точке выпуклость кривой направлена вниз.

ТПусть функция f (x) имеет вторую про-

изводную в некоторой окрестности точки

x0 ,	непрерывную в точке			x0 .	Если
f ''(x0 )= 0		и при переходе	x	через точку
x0	вторая	производная	f ''(x)		меняет
знак, то точка М0 (x0 , f (x0 ))				есть точка

перегиба кривой y = f (x).

Обобщение. Пусть кривая y = f (x) имеет в точке М0 (x0 , f (x0 )) касательную, параллельную оси Oy . Пусть функция f (x) в некоторой окрестности точки x0 , кроме, быть может, самой точки x0 , имеет непрерывную вто-

рую производную. Если		f ''(x)	в точке x0 равна нулю или не существует и
при переходе x через точку x0			производная f ''(x)		меняет свой знак, то точ-
ка М0 (x0 , f (x0 )) - точка перегиба кривой y = f (x).

f ′′(x0 − ∆x)	f (x)	f ′′(x0 )		f ′′(x0 + ∆x)	f (x)	Перегиб
> 0	вып. вниз	0,		> 0	вып. вниз	нет

> 0	вып. вниз	0,		< 0	вып. вверх	есть

< 0	вып. вверх	0,		> 0	вып. вниз	есть

< 0	вып. вверх	0,		< 0	вып. вверх	нет

Исследование функций и построение графиков

191

2.2. Общая схема исследования функции и построения графика

1.Найти область определения функции; найти область значений функции; найти точки пересечения графика с осями координат, указать интервалы знакопостоянства функции.

2.Проверить функцию на периодичность; проверить функцию на четность

инечетность.

3.Исследовать функцию на непрерывность, найти точки разрыва функции

иее односторонние пределы в этих точках; определить наличие горизонтальных, вертикальных и наклонных асимптот.

4.Вычислив первую производную, найти критические точки и интервалы монотонности функции, выделить точки локальных экстремумов.

5.Вычислив вторую производную, найти интервалы выпуклости и точки перегиба графика функции.

6.Построить график.

2.3. Примеры исследования функций
Пример:
Найти экстремумы функции f (x)= 3x2 3 − x2 .
Решение:
f ′(x)= 2	1 −2x ,	2	− 2x = 0 x1 = −1, x2 =1			,
	3 x	3 x
f ′(x) не существует в точке х3 = 0 .
х	(−∞; −1)	-1	(−1;0)	0	(0;1)	1	(1;∞)
f (x)	/ 2		2 0		/ 2		2
f ′(x)	+	0	–		+	0	–
		max		min		max
Вид графика функции f (x)= 3x2 3 − x2 :							2
							1.5
							1
							0.5
					-2	-1	1	2

192	Лекции 1 - 2

Пример:

Построить график функции y = xe−4 x . Решение:

1). x (-∞,∞), х0 = 0; y0 = 0 - точка пересечения с осями.

2). Функция общего вида.

3). f(x) – непрерывна всюду вертикальных асимптот нет.

= lim

= 0

= lim

= 0 ,

x→∞ e4 x x

x→∞ e4 x

y1 = 0 - наклонная (горизонтальная) асимптота при х →∞;

= lim

= ∞ наклонных асимптот при х →-∞ нет.

x→−∞ e4 x x

= 1 .

4). y′ = e-4x − 4xe−4 x = e−4 x (1

− 4x )

, y′ = 0 x

1 .

5). y′′ = -4e-4x

− 4e−4 x

+16xe−4 x = e−4 x (16x −8) ,

y′′ = 0

x 2 =

;

−∞;

;∞

2e2

y′

–

y′′

–

∩

max

∩

перегиб

Вид графика функции y = xe−4 x :

Пример:

Исследовать функцию y =	x3
		и построить ее график.
	2 (x +1)2

Решение:

1). Функция определена всюду, кроме точки x = −1.

Найдём точки пересечения графика с координатными осями. Для этого

	x3
решим уравнения	2(x +1)2 = 0 и y = 0 . х0 = 0; y0 = 0 - точка пересече-

ния с осями.

2). Функция общего вида.

3). Точка x = −1 является точкой разрыва 2-го рода. Отсюда следует, что график функции имеет вертикальную асимптоту x = −1.

Выясним, существуют ли наклонные асимптоты. Вычислим пределы:

k = lim	f (x)	= lim	x2	=	1	;
	x		2(x +1)2		2
x→∞		x→∞

Исследование функций и построение графиков

193

b = lim(

−

x) =

lim

− 2x2 − x

= −1.

2(x +1)2

(x +1)2

x→∞

2 x→∞

y = 1 x −1 является наклонной асимптотой.

x2 (x + 3)

4). Находим производную: y′ =

2(x +1)3

Знак производной определяется знаком дроби

x + 3

. Легко получить, что

x +1

приx < −3 и x > −1

y′ > 0 , а при −3 < x < −1 y′ < 0 . Интервалы возрас-

тания есть (−∞;−1)

и (−1;∞) ;

интервал убывания (−3;−1) . В области оп-

ределения функции производная существует всюду и обращается в нуль приx = −3 и x = 0 .

При x < −3 y′ > 0 , а приx > −3 y′ < 0 . Следовательно, точка x = −3 яв-
ляется точкой максимума.
Находим значение функции при x = −3 :	y( −3 ) =	( −3 )3	= −	27	= −3,375.
		8		8

При переходе	через другую критическую точку x = 0 производная знак
не меняет, т.е.	x = 0 не является точкой экстремума.

5). Находим вторую производную y′′ =

. Видим, что y′′ < 0 при

( x +1)

x < −1, интервал ( −∞;−1)

является областью выпуклости. y′′ < 0 , также

при −1 < x < 0 - это тоже область выпуклости;

y′′ > 0 при x > 0 - это об-

ласть вогнутости.

y′′ = 0 при x = 0 .

В области определения функции y′′существует всюду;

Так как при переходе через эту точку y′′

меняет знак,

то x = 0 есть абс-

цисса точки перегиба. Находим y(0) = 0.

(−∞;−3)

−3

(−3; −1)

−1

(−1;0)

(0;∞)

− 27

y′

–

y′′

–

∩

max

∩

перегиб

x→1+0

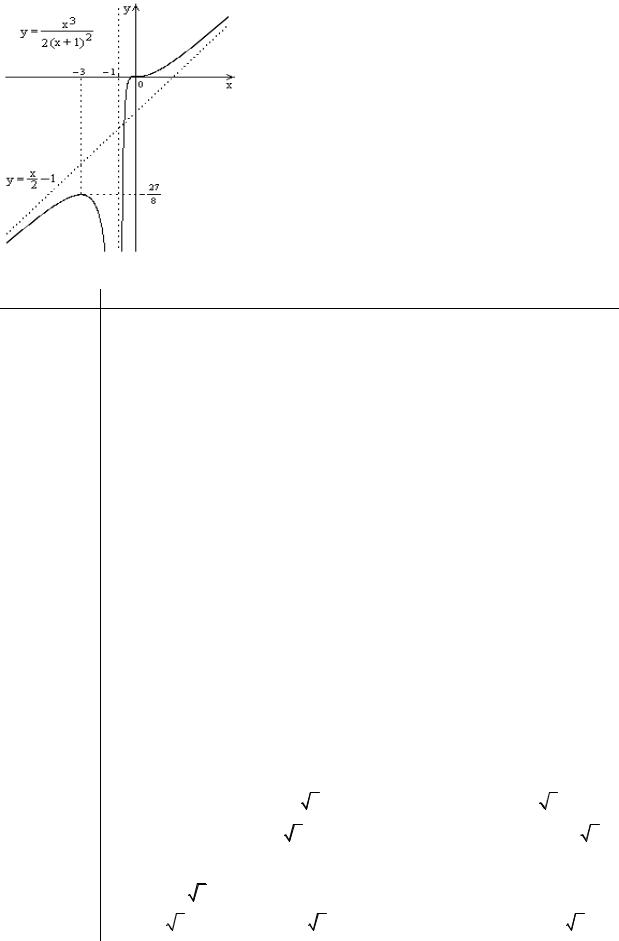
194			Лекции 1 - 2
	График y =	x3


		2 (x +1)2
	имеет вид:

Пример:

Исследовать функцию	y =	x3		и построить её график.
Исследовать функцию	y =	x2	−1	и построить её график.
		x2	−1
Решение:
1). Функция определена всюду, кроме точек x = ±1 .
Точки пересечения графика с координатными осями:					x3		= 0 x = 0	;
Точки пересечения графика с координатными осями:					x2	−1	= 0 x = 0	;
					x2	−1
y = 0 - точка пересечения с осями.
2). Функция нечетная,	f (−x)= − f (x), график симметричен относитель-

но начала координат, достаточно исследовать функцию при x ≥ 0 .

3). Точка x =1 является точкой разрыва 2-го рода, график функции имеет

вертикальную асимптоту x =1, lim f (x)= −∞, lim f (x)= +∞.

x→1−0

Выясним, существуют ли наклонные асимптоты. Вычислим пределы:

k = lim

f (x)

= lim

=1 ;

, т.е. y = x яв-

b = lim

− x

= lim

= 0

−1

x→+∞

x→+∞ x

ляется правой наклонной асимптотой (и левой, так как при операции симметрии прямая переходит сама в себя).

4). Находим производную:	y′ =	x2 (x2 −3)			. Знак производной определя-
		2
	(		x2	)
				−1
ется знаком x2 −3 . При x >	3 y′ > 0 , а при 0 < x <1 и 1 < x <					3 y′ < 0 .
Интервал возрастания - ( 3;∞); интервалы убывания - (0;1)						и (1; 3 ).

В области определения функции производная обращается в нуль при

x = 0 и x =	3 .
При x < 3	y′ < 0 , а приx > 3 y′ > 0 . Следовательно, точка x = 3 яв-

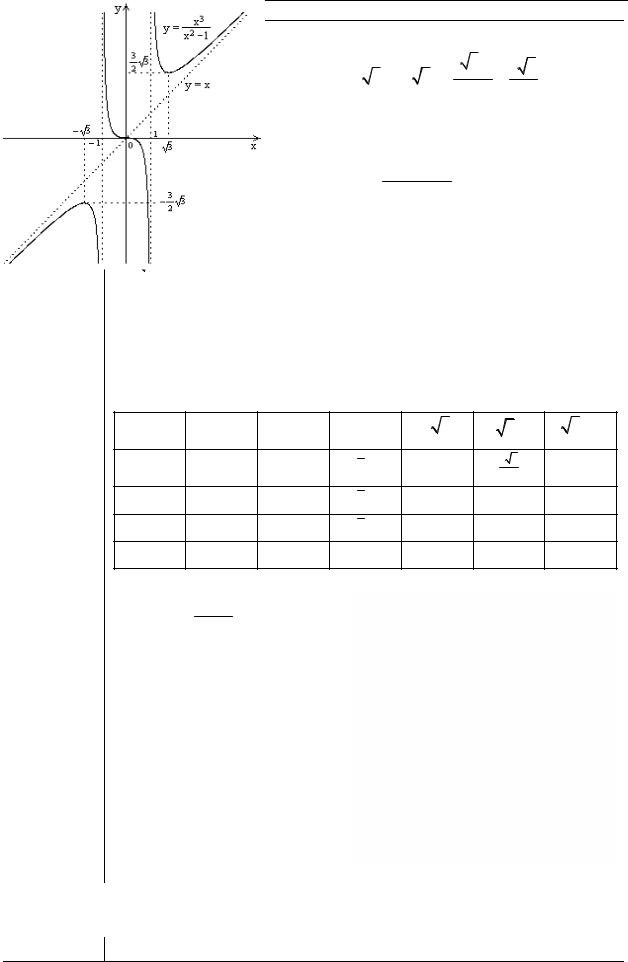
Исследование функций и построение графиков

195

ляется точкой минимума.

Находим значение функции при x =

3 :

y ( 3 )=

(

3 )3

При переходе через критическую точкуx = 0 производная знак не меня-

ет, т.е.

x = 0 не является точкой экстремума.

5). Находим вторую производную y′′ = 2x(x2 +33 ). Видим, что y′′ < 0 при

(

x2 −1

)

0 < x <1, на

интервале

(0;1)

график функции

выпуклый

вверх. При

x >

y′′ > 0 - график функции выпуклый вниз.

В области определения функции y′′существует всюду;

y′′ = 0 при x = 0 .

Так как при переходе через эту точку y′′

меняет знак,

то

x = 0 есть абс-

цисса точки перегиба.

Находим y(0) = 0.

(0;1)

(1; 3 )

( 3; ∞)

−

y′

–

y′′

–

перегиб

∩

min

График

y =

имеет вид:

x2 −1

Пример:

196

Лекции 1 - 2

Исследовать функцию y = 3

2x2 − x3

и построить её график.

Решение:

1). Функция определена при всех x . Для нахождения точек пересечения

с осями записываем уравнения

y = 0 и 3 2x2 − x3

= 0 ; получаем, что ось

Oy пересекается в точке с y = 0 , а ось Ox - в точках x = 0 и x = 2 .

2). Функция общего вида.

3). Точек разрыва нет. Так как нет точек разрыва 2-го рода, вертикальные

асимптоты отсутствуют. Ищем параметры наклонных асимптот.

k = lim

(x)

2x2 − x3

= lim

−1 = −1,

= lim

x→∞

b = lim( 3

2x2 − x3

+ x ) = lim x(1+ 3

−

1 ) =

x→∞

−2

1+ 3

−1

−1 x

= lim

x→∞

−

При вычислении второго предела использовано правило Лопиталя для

раскрытия неопределённости типа

Итак, у графика есть наклонная асимптота; еe уравнение y = −x + 2 .

4). Находим производную:

y′ =

4 −3x

. Знак производной опреде-

x(2 − x)2

ляется знаком выражения

4 −3x

. Видим, что в области x < 0

′

< 0 , при

0 < x <

y′ > 0

и при x >

y′ < 0 .

Получаем, что в области x < 0 функция убывает, при 0 < x <

- возрас-

тает и при

x > 4

- убывает.

′

Находим критические точки.

= 0

при

x = 3 ,

не существует при

x = 0 , x = 2 .

При переходе через x = 0 знак производной меняется с (-) на (+), т.е. это точка минимума.

При x = 0 производная не существует, значит, минимум острый.

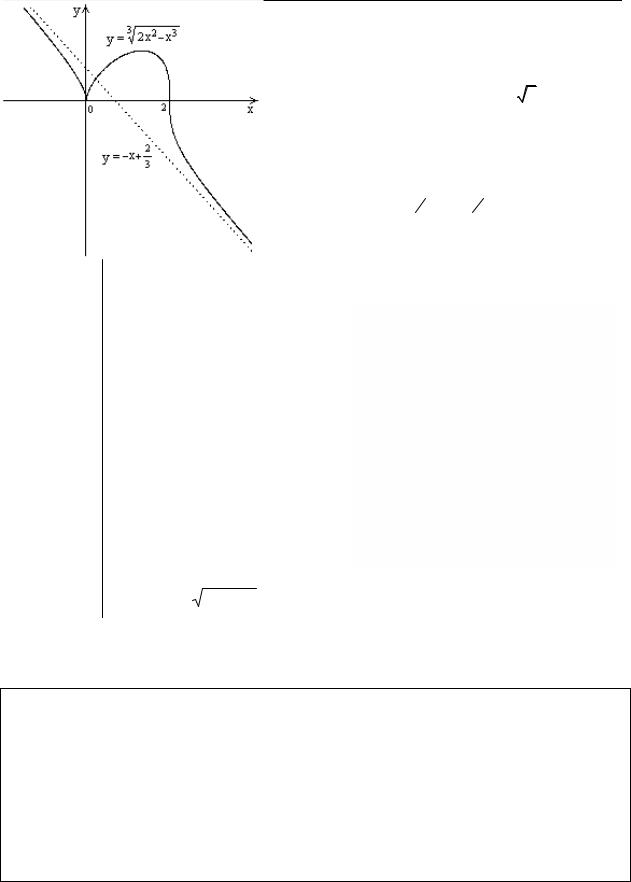
Исследование функций и построение графиков

197

y(0) = 0.

При переходе через вторую критическую точку x = 43 производная ме-

няет знак с (+) на (-) , т.е. при	x =	4	- максимум:		4	=	2	3	4 .
		3		y	3		3

При переходе через x = 2 знак производной не меняется, значит экстремума нет.

5). Находим вторую производную: y′′ = −				8			.
	9x	3	4	(2 − x)	5	3

Видим, что y′′ < 0 приx < 0 ; в этой области график выпуклый; y′′ < 0 при 0 < x < 2, т.е. интервал (0;2) также является областью выпуклости. При x > 2 y′′ > 0 , следователь-

но, при x > 2 график вогнут. Найдём точки перегиба. Вторая производная не существует при x = 0 и приx = 2 .

При переходе через первую точку знак y′′не меняется, а при переходе через вторую – меняется.

Итак, точкой перегиба является точка с координатами x = 2 , y( 2 ) = 0 .

График y = 3 2x2 − x3 имеет вид:

В результате изучения материала, изложенного в этих лекциях,

устудентов должны сформироваться следующие понятия:

точки разрыва,

асимптоты графика,

экстремумы функции,

точки перегиба.

Студент должен уметь:

применять общую схему исследования функции,

строить графики сложных функций.

Лекции 3 - 4 КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ В КОМПЛЕКСНОЙ ОБЛАСТИ

Комплексные числа – расширение множества действительных чисел, широко применяющееся в естественных и прикладных дисциплинах. Использование комплексных чисел позволяет наиболее естественным образом описать многие процессы, в частности, колебательные. Изучение функций комплексного переменного привело к углублению и расширению знаний о функциях действительных переменных и породило множество мощных вычислительных методов.

3.1.Комплексные числа. Основные определения. Алгебраическая форма комплексного числа

3.2.Изображение комплексного числа на плоскости. Тригонометрическая форма комплексного числа

3.3.Формула Эйлера. Показательная форма комплексного числа

3.4.Действия над комплексными числами

3.4.1.Сравнение, сложение и вычитание

3.4.2.Умножение, деление, возведение в целую степень

3.4.3.Комплексное сопряжение

3.4.4.Извлечение корня

3.5.Комплекснозначная функция действительного аргумента

4.1.Многочлены в комплексной области. Корни многочлена

4.2.Основная теорема алгебры

4.3.Примеры решения задач

4.4.Разложение рациональных дробей

4.5.Примеры решения задач

3.1.Комплексные числа. Основные определения. Алгебраическая форма комплексного числа

ОКомплексным числом называют упорядоченную пару действительных чисел z = (x, y ) со следующими свойствами:

1) два комплексных числа z1 = (x1 , y1 ) и z2 = (x2 , y2 ) равны тогда и толь-

ко тогда, когда x1 = x2 и y1 = y2 ;

2) сумма двух комплексных чисел z1 = (x1 , y1 ) и z2 = (x2 , y2 ) определяет-

ся следующим образом:

z1 + z2 = (x1 , y1 )+ (x2 , y2 )= (x1 + x2 , y1 + y2 ).

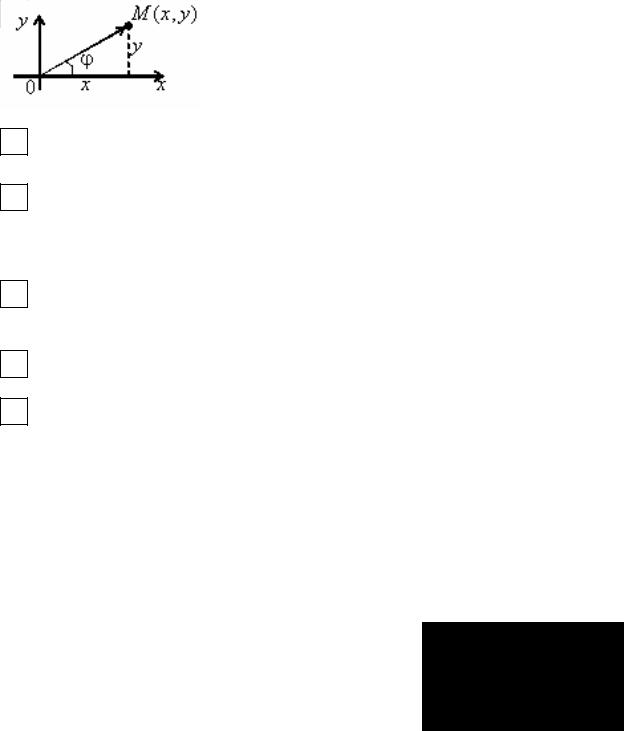
Комплексные числа. Многочлены в комплексной области

199

3) произведение двух комплексных чисел z1 = (x1, y1 ) и z2 = (x2 , y2 ) определяется следующим образом:

z1 z2 = (x1 , y1 ) (x2 , y2 ) = (x1 x2 − y1 y2 , x1 y2 + x2 y1 ).

!Действительные числа содержатся в множестве комплексных чисел, все они являются парами вида (x,0). В дальнейшем будем обозначать

(x, 0)= x .

ОПары вида (0, y) называются чисто мнимыми числами.

ОПара i = (0,1) носит специальное название - мнимая единица. Согласно свойству 3) i i = (−1,0)= −1.

СКаждое комплексное число z = (x, y) можно записать в виде суммы

действительного числа x = (x,0) и чисто мнимого числа iy = (0, y):

z= (x, y)= (x,0)+ (0, y)= x + iy .

ОДействительное число x = Re z называется действительной частью комплексного числа z , действительное число y = Im z называется мни-

мой частью z .

О Комплексное число z =0 , если x = Re z =0 и y = Im z = 0 .

ОЗапись z = x + iy называется алгебраической формой комплексного числа.

3.2.Изображение комплексного числа на плоскости. Тригонометрическая форма комплексного числа

Так как z = (x, y) определяется как пара действительных чисел, то естественной геометрической интерпретацией является изображение комплексного числа точкой М некоторой плоскости с координатами (x, y).

Такую плоскость называют комплексной, ось абсцисс - действительной осью, ось орди-

нат – мнимой осью. При этом устанавливается взаимно-однозначное соответствие между множеством всех комплексных чисел z = (x, y) и множеством

точек М(x, y) или множеством радиус-векторов OM .

200	Лекции 3 - 4
Введем на плоскости XOY полярные координаты (r, ϕ). Длина вектора
OM называется модулем комплексного числа z и обозначается	z	или r :

z = r = OM = x2 + y2 .

Угол ϕ между радиус-вектором OM и положительным направлением оси OX называют аргументом комплексного числа z: ϕ = Arg (z). Угол ϕ

определяется неоднозначно, с точностью до слагаемого 2πk . Удобно рабо-

тать с приведенным аргументом ϕ = arg (z), 0 ≤ϕ < 2π (либо −π ≤ϕ <π ).

Для числа z =0 +i0 аргумент не определён. При этом аргумент комплексного числа определяется следующим образом:


						y	, если x > 0,
			arctg
			arctg			x
						x
						y
						y	+π, если x	< 0, y > 0,	(для 0 ≤ϕ < 2π ).
			ϕ = arctg
			ϕ = arctg			x
						x
						y	−π, если x	< 0, y < 0.
			arctg
			arctg			x
						x
Практически, для определения ϕ = arg( z ) решают систему уравнений
cosϕ =	x	,	sinϕ =	y	и изображают			z вектором,	чтобы определить, в каком
cosϕ =	r	,	sinϕ =		и изображают			z вектором,	чтобы определить, в каком
	r			r

квадранте лежит точка. Так как x = r cosϕ , y = r sinϕ , то комплексное число z = x + iy можно записать в следующем виде: z = r(cosϕ +i sinϕ) , которое называют тригонометрической формой записи комплексного числа.

3.3.Формула Эйлера. Показательная форма комплексного числа

Используя формулу, полученную Эйлером: eiϕ = cosϕ +isinϕ (которая будет доказана позже, при изучении теории рядов), можно получить еще одну, показательную, форму комплексного числа: z = r eiϕ .

Комбинируя eiϕ = cosϕ +isinϕ и e−iϕ = cos(−ϕ)+ isin (−ϕ)= cosϕ −isinϕ ,

можно получить выражения cosϕ =	eiϕ + e−iϕ	, sinϕ =	eiϕ − e−iϕ	.
	2		2i

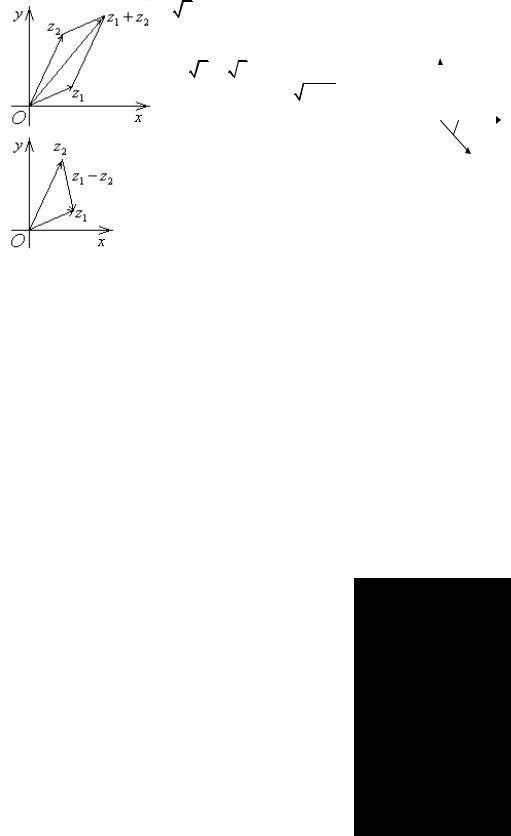
Комплексные числа. Многочлены в комплексной области

201

Пример:

Записать число z =

2 −i 2

в различных формах. Дать геометрическую

интерпретацию.

Решение:

Алгебраическая форма: z =

2 −i

2 ;

тригонометрическая

форма:

r =

= 2 + 2 = 2 ;

= cos

7π

−

= sin

ϕ=−π

7π

откуда ϕ = arg( z ) =

r=2

7π

z = 2

−i

= 2 cos

+isin

;

7π

показательная форма:

z = 2e 4 .

3.4. Действия над комплексными числами

Операции в арифметической форме производятся в соответствии с усло-
вием i i = (−1,0) = −1	и	с обычными правилами алгебры. Обозначим
z1 = (x1 , y1 ) = x1 + iy1 , z2 = (x2 , y2 ) = x2 + iy2 .
3.4.1. Сравнение, сложение и вычитание
Сравнение чисел	в	алгебраической форме:

z1 = z2 , если x1 = x2 и y1 = y2 .

Если числа заданы в тригонометрической или показательной форме: z1 = r1 (cosϕ1 + i sinϕ1 ) ,

z2 = r2 (cosϕ2 + i sinϕ2 ) или z1 = r1 eiϕ1 , z2 = r2 eiϕ2 ,

то z1 = z2 , если r1 = r2 ,

ϕ1 =ϕ2 + 2πk; k Z .

Сложение в алгебраической форме:

z1 + z2 = (x1 + x2 , y1 + y2 )= (x1 + x2 )+ i(y1 + y2 ).

Вычитание определяется как действие, обратное сложению: пусть z = z1 − z2 ,

тогда

z1 = z + z2 , z1 = x1 + iy1 = x + x2 + i(y + y2 ),

202	Лекции 3 - 4

откуда

z1 − z2 = (x1 − x2 )+ i(y1 − y2 ).

С геометрической точки зрения сложение (вычитание) комплексных чисел равносильно сложению (вычитанию) изображающих их векторов.

3.4.2.Умножение, деление, возведение в целую степень Умножение в алгебраической форме:

z1 z2 = (x1 + iy1 )(x2 + iy2 ) = x1 x2 + ix2 y1 + ix1 y2 + i2 y1 y2 = =(x1x2 − y1 y2 )+ i(x1 y2 + x2 y1 ).

В тригонометрической форме:

z1 z2 = r1 r2 (cosϕ1 + i sinϕ1 ) (cosϕ2 + i sinϕ2 ) =

=r1r2 (cosϕ1 cosϕ2 - sinϕ1sinϕ2 + i( sinϕ1 cosϕ2 + cosϕ1sinϕ2 ) =

=r1r2 (cos(ϕ1 +ϕ2 ) + i sin(ϕ1 +ϕ2 )) ,

т.е.

z1 z2 = r1 r2 (cos(ϕ1 +ϕ2 ) + i sin(ϕ1 +ϕ2 )).

В показательной форме:

z1 = r1 eiϕ1 , z2 = r2 eiϕ2 , z1 z2 = r1 r2 eiϕ1 eiϕ2 = r1 r2 ei(ϕ1 +ϕ2 ) ,

т.е. модуль произведения комплексных чисел равен произведению модулей, а аргумент – сумме аргументов сомножителей.

Деление определяется как действие, обратное умножению:

z= z1 = ((x1 , y1 )) = (x, y), z2 x2 , y2

откуда z1 = z z2 .

Запишем соответствующую формулу для алгебраической формы комплексного числа:

z1 = z z2 = (x1 , y1 )= (xx2 − yy2 , xy2 + x2 y),

откуда получаем систему двух линейных уравнений с двумя неизвестными:

xx2 − yy2 = x1xy2 + x2 y = y1

Решаем, используя формулы Крамера:

-y2

∆ = x22 + y22 ≠ 0; x =

; y =

x22 + y22

z1		=	x1 x2 + y1 y2			+ i	x2 y1 − x1 y2			.
z			2	+ y	2		2	+ y	2
	2		x		2		x		2
			2				2

Комплексные числа. Многочлены в комплексной области					203
В тригонометрической форме:
	z1	=	r1	[cos(ϕ1 −ϕ2 ) + i sin (ϕ1 −ϕ2 )] ,
	z2
			r2

в показательной форме:

z1 = r1 еi( ϕ1 −ϕ2 ) ,

z2 r2

т.е. модуль частного комплексных чисел равен частному модулей, а аргумент

– разности аргументов делимого и делителя.

Возведение в целую степень выводится на основе обобщения операции умножения:

z = r(cosϕ + i sinϕ ) , z2 = z × z = r2 (cos 2ϕ + i sin2ϕ ) ;

zn = z × z...× z = r2 (cos2ϕ +isin2ϕ) z × z...× z = rn (cos nϕ + i sin nϕ) ;

n	n-2
zn = rn (cos nϕ + i sin nϕ) ;

z = reiϕ , zn = r neinϕ .

Сравним последние две формулы:

еinϕ = cos nϕ + isin nϕ , с другой стороны:

еinϕ = (еiϕ )n = (cos ϕ + i sin ϕ)n

(cos ϕ + i sin ϕ)n

= cos nϕ + isin nϕ . Послед-

нее соотношение называется формулой Муавра.

Пример:

Найти z11 , если z =1−i .

Решение:

arg z = −π

( z расположено в IV квадранте).

2 e−i

Тогда z =

4 .

−i

11π

= ( 2)

= 2

cos

+i sin

−

3π

−i sin

3π

−i

(1+i).

= 2 2

cos

= 2 2

−

= −2

3.4.3. Комплексное сопряжение

О	Комплексным числом, сопряженным к z = x + iy , называется комплекс-
	ное	число z , отличающееся от z только знаком мнимой части:

	z = x −iy .
Свойства операции сопряжения:
1°.			= z ;
		z
2°.		z = z тогда и только тогда, когда z - действительное число;

204

Лекции 3 - 4

3°.

z1 ± z2

4°.

z1 z2

(z )

5°.

(z2 )

6°.

z = x2 + y2 .

Докажем некоторые соотношения.

В алгебраической форме: z = x +iy, z = x - iy .

Вычислим:

а)

z + z = (x +iy)+ (x −iy)= 2x , следовательно,

z + z = 2x ; z − z = 2iy ;

б)

zz = (x +iy)(x −iy)= x2 + y2 , следовательно:

z z = x2 + y2 .

Тогда

z z

(x1x2 + y1 y2 )

+ i(x2 y1

− x1 y2 )

x22

+ y22

z2 z2

x1x2 + y1 y2

+ i

x2 y1 − x1 y2

+ y2

x2 + y2

В тригонометрической форме:

z =

(cosϕ +isinϕ) ;

(cosϕ −isinϕ) =

(cos(−ϕ) + isin(−ϕ)) .

В показательной форме:

z =

eiϕ ,

e−iϕ .

Геометрически - комплексное сопряжение есть операция симметричного отражения вектора, соответствующего числу z относительно действительной оси.

Вывод: пользуясь алгебраической формой комплексного числа, можно производить операции сложения, умножения, вычитания по обычным правилам умножения многочленов. При делении комплексных чисел эффективно использовать прием умножения числителя и знаменателя на число, сопряженное знаменателю.

Свойства операций сложения и умножения:

1°. z1 + z2 = z2 + z1 ,

2°. (z1 + z2 )+ z3 = z1 + (z2 + z3 ),

3°

4°.

5°.

z1z2 = z2 z1 ,

(z1z2 )z3 = z1 (z2 z3 ),

(z1 + z2 )z3 = z1z3 + z2 z3 .

Комплексные числа. Многочлены в комплексной области								205
Пример:	и arg z для числа:
Найти z	и arg z для числа:	z =1+i .						z=1+i
Решение:			y		π		1	z=1+i
z =1+i ,	z = 1 +1 = 2 ,	α = arctg	y	= arctg1 =	π	.	1
			x		4			α
							0	α
							0	1

3.4.4. Извлечение корня

Определяется как действие обратное возведению в степень.
Число b называется корнем n-ой степени из числа z					и обозначается b = n z ,
если bn = z .
Пусть z = reiϕ ,	а b = ρeiϕ и r, θ известны. Найдемρ,θ .					Два комплексных
числа равны bn	= z , если равны их модули			ρn = r ρ = n		r	и аргументы от-
личаются на	2kπ . nθ =ϕ	+ 2kπ θ =		ϕ + 2kπ ,	n reiϕ		= n r ei	ϕ+2кπ	или
								n
	ϕ	2π		n

окончательно n	reiϕ = n r ei( n +k		) .
		n

Здесь k может принимать все возможные целые значения.

Различных (неодинаковых) значений корней будет ровно n, и они будут соответствовать значениям k = 0, 1, 2, …, n-1.

	ϕ
b = n r ei n		, k = 0 ,
0
	ϕ	2π
b = n r ei( n		+	n ) , k =1,
1
	ϕ		2π
b = n r ei( n		+2 n ) , k = 2 ,
2
	= n r ei	ϕ	2π	) , k = n −1.
b	= n r ei	( n	+(n−1) n	) , k = n −1.
n−1

Если же, например, k = n , то

аналогично

Вывод: значений.

b = n r ei(	ϕ		2πn		ϕ		ϕ
b = n r ei(	n	+	n	)	= n r ei( n	+2π )	= n rei n ei2π =
n
					ϕ
	=		n rei n 1 = b → b = b ,
					0		n 0

bn+1 = b1 и т.д.

корень n-й степени из комплексного числа имеет n различных

206	Лекции 3 - 4

!Числа b0 ,b1 ,...,bn−1 имеют одинаковый модуль, и так как аргументы отличаются, следовательно, значения корня будут изображаться точками на окружности.

Пример:

Вычислить и изобразить на комплексной плоскости 4 i Решение:

Запишем число i в показательной форме:

πk

; z = 4 w =

+2πk

w = i = e

2 = e4

= e

2 .

Возможно четыре различных значений корня, соответ-

ствующих

k =0,1, 2, 3 :

= ei 8 , (k = 0) ,

= ei(

z = ei( 8 +

2 ) , (k =1) , z

8 +π ) , (k = 2) ,

+3 2 ) , (k = 3) . z

получен

из корня

z0 поворотом на

против часовой стрелки, z2 из z0

поворо-

том на π и т.д.

Пример:

Вычислить 6 1 + i 3 ; изобразить схематично значения корня на комплексной плоскости. Решение:

w =1 + i 3 = 2ei					π
w =1 + i 3 = 2ei					3 ;
1						π	+ 2πk
	z	= 6 2 = 2		; θ =		3		; k = 0,1, 2,3, 4,5 .
			6			3
			6				6
							6

Начальный аргумент при k = 0 равен θ = 18π .

Значения корня:

2 ei

7π

2 ei

13π

z = 6

, z

= 6

, z = 6

19π

2 ei

25π

2 ei

31π

= 6

2 ei 18 , z = 6

18 , z = 6

18 .

Соответствующие 6 точек располагаются в вершинах правильного шестиугольника на окружности радиусом 6 2 .

Пример:

Решить уравнение z 2	+ z +1 = 0 .
Используя формулу	для	решения квадратного уравнения и полагая
−1 = i , имеем: z =	−1 + i	3 , z	2	= −1 −i 3 .
1	2		2	2
	2			2

Рассмотренное уравнение имело вещественные коэффициенты. Пусть коэффициенты комплексные.

Комплексные числа. Многочлены в комплексной области

207

Пример:
	Решить уравнение z 2 + (−3 + i2)z + 5 −i = 0 .
	По формуле квадратного уравнения
	z =	−( −3 + 2i ) + ( 2i −3 )2 −4( 5 −i )			= 3 −2i + −15 −8i .
		2			2
	Число, стоящее под знаком квадратного корня, можно было бы записать
	в показательной форме, а затем по известному правилу извлечь из него
	корень. Однако можно поступить иначе. Положим
	−15 −8i = x + iy.
	Возводим обе части в квадрат и находим
	−15 −8i = x2 − y2 + 2ixy , откуда x2				− y 2 = −15 ; 2xy = −8 .
	Эта система имеет решения: x1 =1, y1				= −4, x2 = −1, y2 = 4; поэтому
	z = 3 − 2i + (1 − 4i) = 2 −3i, z		2	= 3 − 2i + (−1 + 4i) =1 + i.
	1	2	2		2
		2			2

3.5. Комплекснозначная функция действительного аргумента

ОЕсли каждому действительному t ставится в соответствие комплексное z,

то z = z(t) называют комплекснозначной функцией действительного аргумента.

z = eiϕ - комплекснозначная функция действительного аргумента ϕ . В

алгебраической форме:	z(t) = x(t) + i y(t) . Так как z(t)	соответствует вектору
с координатами х(t) и	y(t) , то задание функции z(t)	эквивалентно заданию

вектора функции скалярного аргумента.

Теория комплекснозначных функций скалярного аргумента совпадает с теорией векторной функции скалярного аргумента.

z'(t) = x′(t) + iy′(t) - формула дифференцирования комплекснозначной функции.

4.1. Многочлены в комплексной области. Корни многочлена

О Многочленом называется функция вида:

Pn( z ) = a0 zn + ... + an−2 z2 + an−1z + an ; a0 ≠ 0 ,

где n – степень многочлена (n – натуральное), а коэффициенты a0 ,..., an

могут быть как действительными, так и комплексными, z – комплексная переменная. При a0 =1 многочлен называется приведённым.

О Рациональной дробью называется отношение двух многочленов

208	Лекции 3 - 4

Pm ( z ) = b0 zm + b1 zm−1 + ... + bm−1 z + bm . Pn( z ) a0 zn + a1 zn−1 + ... + an−1 z + an

При m < n дробь называется правильной, при m ≥ n дробь называется не-

правильной.

Неправильную дробь всегда можно разложить на сумму многочлена и правильной дроби; вид многочлена находится при делении «уголком» или по схеме Горнера. Свойство деления можно записать следующим образом:

Pm ( z ) = Ql ( z ) + Rp ( z ) . Pn ( z ) Pn ( z )

Здесь Ql ( z ), Rp ( z )- многочлены степени l и p соответственно;

Ql ( z ) - частное (целая часть дроби); l ≤ m l + n = m , Rp ( z ) - остаток ( p < n ).

Пример:

2z3 +3z2 +6z −3

= 2z +1+

3z −4

z2 + z +1

Если Rp

( z ) =0

Pm( z )

= Ql ( z ) ; Pm( z ) = Pn( z ) Ql ( z ) . В этом случае

Pn ( z )

говорят о делении нацело.

ОКорнем многочлена Pn( z ) называют число z0 , удовлетворяющее уравнению Pn( z ) =0 или в развёрнутом виде.

a0 zn + ... + an−2 z2 + an−1z + an = 0; a0 ≠ 0 .

Данное уравнение является алгебраическим уравнением n-й степени.

ТТеорема Безу. Остаток, получаемый при делении Pm( z )на (z-a), равен

Pm( a )

Доказательство:

По условию Pn (z) = P1 (z) = z-a . По основному свойству: Ql (z) = Qm-1(z) , Rp ( z ) = R0 ( z ) = R0 . Тогда Pm( z ) = Qm−1( z ) ( z − a ) + R0

Положим z = a , тогда получим равенство Pm (a) = R0 , что и требовалось доказать.

СДля того чтобы многочлен Pn( z ) делился на выражение (z-a) без остат-

ка, необходимо и достаточно, чтобы число z = a было корнем этого мно-

гочлена. Таким образом, если z = z0	- корень Pn( z ), то
Pn( z ) =( z − z0 ) Qn−1( z ) . Другие корни Pn( z )	следует искать из уравне-
ния: Qn-1 (z) = 0 и т.д.

Комплексные числа. Многочлены в комплексной области

209

Пример:

Проверить, что z =1 является корнем многочлена

P (z) = z3

+ z 2 + 3z −5

и найти другие корни многочлена.

Решение:

P3 (1) =1 +1 + 3 −5 = 0 , то

z =1 является корнем

Так

как

многочлена

P3 (z) и многочлен P3 (z) делится на z −1 без остатка.

−

z 3

+ z 2

+ 3z − 5 | z −1

z 3

− z 2

z 2 + 2z + 5

− 2z 2

+ 3z

P (z) = (z −1)(z2

+ 2z + 5).

2z 2

− 2z

− 5z − 5

5z − 5

Для

отыскания

других

корней

многочлена

решим

уравнение

z 2

+ 2z + 5 = 0 :

z = −1 ±

1 −5 = −1 ± 2i.

Итак,

многочлен

(z) = z3

+ z 2 + 3z −5 имеет один действительный корень

=1 и два

комплексно-сопряженных корня z2 = −1 + 2i , z3 = −1 − 2i.

ОЕсли Pn ( z ) =( z − z0 )k Qn−k ( z ) , где Qn-k ( z0 ) ≠ 0, то z0 называют корнем кратности к многочлена P n (z) .

Пример:

P 3 (z) = z3 +3z2 +3z +1 = (z +1)(z +1)(z +1) = (z +1)3 ; z0 = −1- корень кратности 3.

4.2. Основная теорема алгебры

ТЛюбой многочлен P n( z ) при n ≥1 имеет хотя бы один корень (действи-

тельный или комплексный).

С1). Каждый многочлен Pn ( z ) имеет ровно n корней, если каждый корень считать столько раз, какова его кратность.

2). (с учетом теоремы Безу) Всякий многочлен n-й степени разлагается на n линейных множителей вида z − zk и множитель, равный коэффици-

енту при zn . Pn ( z ) = a0 ( z − z1 )( z − z2 )...( z − zn ) .

Для случая кратных (повторяющихся) корней формула группируется следующим образом:

210							Лекции 3 - 4
P ( z ) = a	n	( z − z	)k1 ( z − z	2	)k2 ...( z − z	m	)km	(*)
n	n	1		2		m
здесь zi – корни кратности ki , i =1,2,…,m, k1 + k2 + ...+ km = n
Рассмотрим случай многочленов с действительными коэффициентами.

Т	Если многочлен Pn ( z ) с действительными	коэффициентами имеет ком-
	плексный корень z0 = α +iβ кратности к,	то он имеет и комплексно-
	плексный корень z0 = α +iβ кратности к,	то он имеет и комплексно-

сопряженный корень z0 =α −iβ той же кратности.

Вывод: комплексные корни многочлена с действительными коэффициентами появляются сопряженными парами.

ТМногочлен с действительными коэффициентами разлагается на линейные и квадратичные множители с действительными коэффициентами. Рассмотрим линейные множители вида ( z − zi ) , где zi - действительное

число, и объединим множители вида (z − zl )(z − zl ) , где zl - комплексное

число. Тогда ( z − zl ) ( z − zl ) = z2 − z( zl + zl ) + zl zl .

Но zl + zl = (α + iβ) + (α −iβ) = 2α, zl zl =(α + iβ ) (α −iβ ) =α2 + β2

являются действительными числами, обозначим их p и q соответственно. Тогда (z − zl )(z − zl ) = z2 + pz + q, где p, q – действительные числа, а

квадратный трехчлен имеет только комплексные корни и не разлагается на линейные множители с действительными коэффициентами. Таким образом, многочлен Pn (z) с действительными коэффициентами имеет следующее раз-

ложение:

Pn( z ) = a0 ( z − z1 )s1 ( z − z2 )s2 …( z − zi )si ( z2 + p1 z + q1 )k1 …( z2 + p j z + q j )k j ,

где s1 + s2 +…+ si + 2k1 +…+ 2k j = n .

!Данное выражение представляет собой произведение множителей двух типов:

1). Линейные множители ( z − zi )si , где zi - действительный корень крат-

ности Si .				(z2 + pz + q)kj с
2). Квадратичные	множители					действительными
коэффициентами p,	q и отрицательным дискриминантом D = p2 -4q < 0 .
	2		k j			k j
Данные множители	(z	+ pz + q)					соответствуют
				= (z − z j ) (z − z j )
паре комплексно-сопряженных корней z j ,z j					кратности k j .

Комплексные числа. Многочлены в комплексной области

211

Пример:

Разложить на множители P(x) = х3 +1 .

Линейные множители (действительные корни): x1 = −1 ; х3 +1 делится на х+1 без остатка, P (х)= х3 +1 = (х+1)(х2 − х+1) , у трехчлена действительных корней нет.

Найдем пару комплексно-сопряженных корней:

x2,3 =

1± 1-4

1± −3

1±

3 −1

1±i 3

1+i 3

1−i 3

P (x)

= (x +1) x −

x −

4.3. Примеры решения задач

Пример:

Разложить на множители многочлен P4 (z) = z 4 +1.

Решение:

Очевидно, действительных корней многочлен не имеет, находим комплексные корни:

	4					iπ									i( π+2kπ )
z	4		= −1+ 0i = e			iπ	;	4	−1	+ 0i = e							4			; где					k = 0;1;2;3.
z			= −1+ 0i = e				;		−1	+ 0i = e										; где					k = 0;1;2;3.
											π					3π							5π							7π
Корни многочлена:									z = ei 4				; z		= ei			; z		= ei					; z			= ei				.
Корни многочлена:									z = ei 4				; z	2	= ei	4		; z	3	= ei			4		; z		4	= ei		4		.
									1					2					3								4
Пары z1 , z4 ; z2 , z3								- сопряженные: z 4 +1 = (z − z1 )(z − z4 )(z − z2 )(z − z3 );
объединим попарно сомножители:
z4 +1 = (z2 − z(z + z								4	) + z z		4	)(z2 − z(z					2	+ z			) + z			2	z	) ,
					1			4		1	4						2			3				2	3
z		+ z		4	= cos π +i sin π +cos 7π +i sin 7π =																				=		2		+i		2		+	2	−i	2	= 2 ,
z		+ z			= cos π +i sin π +cos 7π +i sin 7π =																				=				+i				+		−i		= 2 ,
1					4			4					4					4									2			2				2		2
z1 z4					4			4					4					4									2			2				2		2
z1 z4					=1.
Аналогично, z2 + z3								= −		2,			z2 z3 =1.
Тогда					P ( z ) = z 4 +1 = ( z 2						+			2z +1)( z 2						−		2z +1).
					n

212

Лекции 3 - 4

Пример:

Дать геометрическое описание множества всех

точек

комплексной

плоскости, удовлетворяющих условиям:

1 ≤

≤ 5

≤ 0

Imz

Решение:

Запишем

в алгебраической форме z = x + yi , тогда

из условия :

1 ≤

+ y

≤ 5

≤ x

+ y

≤ 5

−5 −1 0 1 5

y ≤ 0

≤ 0

Геометрически: нижняя половина кольца с внутрен-

ним радиусом R1

= 1 и внешним R2 = 5.

Пример:

Представить

тригонометрической

показательной

формах числа

= 2 + 2 i; z

= 5 −12i;

= −i.

Решение:

eiϕ1

z = x + iy =

;

= π ,

1 + 1 = 1

= ei

π + i sin π ;

ϕ = arctg

;

= cos

25 +144 =

169 =13 ;

ϕ2

−

;

ϕ2

− угол, лежащий в IV четверти.

= arctg

arctg

−

= 13e

=13 cos arctg

−

+i sin arctg −

;

1 + 0 = 1;

ϕ3 = −

;

z3 = e

−i

= cos

−i sin

Пример:

Выполнить действие:

+ 2

i 9

+ 2i8 +i7

+11

i 2 + 2

Решение:

Поскольку i2

= −1;

=1,... i9

= i,

i8 = +1, i7

= −i.

+ 2

−1 + 2

i9 + 2i8 + i7 +11

i2 + 2

+ 2

−i +11

−1 +

= 13i +i −i = 13i .

Комплексные числа. Многочлены в комплексной области

213

Пример:

Вычислить 4

2 +

2i .

Решение:

ϕ+2πk

z = 4

; где k = 0; 1; 2; 3 .

= 2 + 2 = 2; ϕ = arctg

π ;

ϕ - угол, лежащий в I четверти.

9π

17π

25π

z = 4 2ei

; z = 4 2ei

; z = 4

2ei

; z = 4 2ei

Пример:

Разложить многочлен

x4 + 6x3 + 25x2 + 68x

на множители с действи-

тельными коэффициентами.

Решение:

x1 = 0 . Подбором находим

x2 = −4 , с помощью деления “уголком” по-

лучаем:

x4 + 6x3 + 25x2 + 68x

= x

+ 2x +17; D = 4 − 4 17 < 0 .

x( x + 4 )

Тогда разложение имеет вид :

x4 + 6x3 + 25x2 + 68x = x( x + 4 )( x2 + 2x +17 ) .

Пример:
	Решить биквадратное уравнение z4 + 4z2 + 3 = 0 .
	Решение :	(		)(		)	= 0 .
	z4 + 4z2 + 3 =	(	z2	)(	z2 + 3	)
	z4 + 4z2 + 3 =		z2	+1	z2 + 3
	z1,2 = −1 = 0 ± i ; z3,4 = − 3 = 0 ± i 3 .

Пример:

Разложить многочлен на квадратные множители при условии, что задан один из корней.

x4 +8x3 + 21x2 +8x + 20; x1 = −4 + 2i .

Решение:

Поскольку для многочлена с действительными коэффициентами корни появляются только сопряженными парами, то x2 = −4 − 2i . Соответст-

вующий квадратный трехчлен:

( x − x1 )( x − x2 ) =( x + 4 − 2i )( x + 4 + 2i ) =(( x + 4 )2 − 4i2 ) =

= x2 +8x + 20.

Делением начального многочлена получаем :

x4 +8x3 + 21x2 +8x + 20 =( x2 +8x + 20 )( x2 +1).

214

Лекции 3 - 4

Пример:

Найти множество точек комплексной плоскости, удовлетво-

ряющих условию

z −i

=1.

Решение:

z −1 = x + iy − i = x + i( y −1) = x2 + ( y −1)2 =1,

x2 + ( y −1)2 =1. Следовательно, искомое множество со-

стоит из точек окружности единичного радиуса, центр кото-

рой имеет координаты (0;1) .

4.4. Разложение рациональных дробей

Т	Всякую правильную рациональную дробь можно разложить на сумму
	простейших дробей четырех типов:

		A	;	A	;	Bx +C	;	Bx +C	, p2 − 4q < 0 .
				(x - a)k		x2 + px + q		(x2 + px + q)k
		x - a

При этом каждому действительному корню а кратности m в разложении знаменателя Pn (x) соответствует сумма

A1	+	A2	+ ...+	Am	.
		(x - a)2		(x - a)m
x - a

Каждой комплексно сопряженной паре корней zi ,zi кратности m соответствует сумма

	M1x + N1	+		M 2 x + N2	+ ...+	Mm x + Nm	.
			(x2 + px + q)2			(x2 + px + q)m
	x2 + px + q
Коэффициенты Ai ,Mi ,Ni				находятся методом неопределённых коэффи-

циентов при одинаковых степенях x в числителях после приведения к общему знаменателю правой части разложения.

Пример:

Разложить на суммы простейших дробей правильную дробь

(

x2 −

1 (x −2)

)

Преобразуем знаменатель, пользуясь формулой разности квадратов:

(

)

− 2)= (x −1)(x +1)(x − 2);

−1

(x −1)

, (x +1)

,(x −2)

;

x −1

x +

x −

(

)

−

1 (x

−

x −1 x +1 x −2

Комплексные числа. Многочлены в комплексной области							215

	x = A1 (x +1)(x −2) + A2 (x −1)(x − 2) + A3 (x −1)(x +1) .
	Первый способ нахождения коэффициентов.
	Равенство справедливо для любого x , в том числе и для
	x= −1: −1 = A2 (−2)(−3)
	x = 2: 2 = A3 (1) 3
	x =1: 1 = A1 2 (−1)
	A = − 1		, A = − 1		, A = 2
1		2	2	6	3	3
		2		6		3

Второй способ нахождения коэффициентов.

Многочлены равны, когда равны коэффициенты перед одинаковыми степенями x.

x2 : A + A + A = 0;
1		2			3
x1 : −A −3A =1;
1				2
x0 : −2A +				2A − A = 0
	1				2	3
A = − 1				, A = − 1 ,				A = 2 .
1		2			2	6		3	3
		2				6			3
Третий способ:
Комбинация первого и второго способов.
Ответ:					x			= −	1	−	1	+	2	.
Ответ:	(	x			)		2)	= −		−		+		.
	(				)
			2	−	1 (x	−			2(x −1)		6(x +1)		3(x − 2)
			2	−		−			2(x −1)		6(x +1)		3(x − 2)

Пример:

x2 −1 = ? x(x2 +1) 2

Порядок многочлена x (x2 +1)2 в знаменателе равен 5.

;

B1x + D1

B2 x + D2

+1)

;

(x2 +1)

(x2 +1)2

x2 −1

A B x + D B x + D

;

x(x2 +1)2

(x2 +1)

(x2 +1)2

x2 −1 = A( x2 +1 )2 +(B1 x + D1 )x( x2 +1) +(B2 x + D2 )x ; x =0 : A = −1;

x4 : A + B1 = 0 ; x3 :D1 = 0 ;

x2 : 2 A + B1 + B2 = 1 ;

x: D1 + D2					= 0;
A = −1, B1 =1, D1 = 0, D2 = 0, B2 = 2 .
	x2 −1				= −	1	+	x	+			2x			.
(		2	)	2		x		x2 +1		(		2	)	2

x x			+1								x		+1

216 Лекции 3 - 4

Пример:

Разложить рациональную дробь на сумму простейших, предварительно

выделив целую часть:

x3 − x +8

x3 − 2x2 + x + 4

Решение:

x3 − x +8

2x2 − 2x + 4

Разделив «уголком», получим:

=1 +

−

2x2 + x + 4

− 2x2 + x +

Разложим

на

множители

знаменатель:

= −1;

x3 − 2x2 + x + 4

= x2

− 3x + 4;

x +1

x3 − 2x2 + x + 4 = (x +1)(x2

− 3x + 4).

2x2 − 2x + 4

Bx + C

= Ax2

− 3Ax + 4 A + Bx2 + Bx + Cx + C .

(x +1)(x2 − 3x +

x +

x2 − 3x +

x2 :

A + B = 2

A =1;

x1 : −3A + B +C = −2

B =1;

4A +C = 4

C = 0.

Искомый результат:

x3 − x +16

1 +

x3 − 2x2 + x + 4

x +1

− 3x +

4.5. Примеры решения задач

Пример:

Разложить на суммы простейших дробей дробь x310+ x .

Решение:

Знаменатель P3 (x) = x3 + x , корни x1 = 0; x2,3 = 0 ± i .

P3 (x) = x(x2 +1).

10	=	A	+	Bx +C	=	Ax2 + A + Bx2 +Cx	.
x3 + x		x		x2 +1		x( x2 +1)

Приравниваем числители и коэффициенты при одинаковых степенях x :

10 = Ax2 + A + Bx2 + Cx;

: A + B =

A =10;

C = 0

B = −10; .

A =10

C = 0,

тогда искомое разложение имеет вид:

−

10x

x3 + x

x2 +1

Комплексные числа. Многочлены в комплексной области

217

Пример:
Разложить неправильную дробь на сумму многочлена и простейших
дробей.
	x4 + 3x3 + 3x2 + 9			= x +			9 −9x		.
	x3 + 3x2 + 3x + 9						(x + 3)(x2 + 3)

	9 −9x	=		A		+	Bx + C	.
	(x + 3)(x2 + 3)		x +		3
							x2 + 3

9 −9x = Ax2 + 3A + Bx2 + Cx + 3Bx + 3C.

x2 : A + B = 0

A = 3;

B = −3;

:C +3B = −9

C = 0,

:3A +3C = 9

Ответ:

+ 3x3 + 3x2 + 9

= x +

−

+ 3x2

+ 3x + 9

x + 3

2 + 3

Пример:

Разложить правильную рациональную дробь на сумму простейших дробей

3x2

(x −1)2 (x2 + x +1)

3x2

Cx + D

(x −1)2 (x2 + x +1)

x −1

(x −1)2

x2 + x +1

Ax3 − A + Bx2 + Bx + B + Cx3 − 2x2 + Cx + Dx

2 − 2Dx + D

(x −

1)2 (x2 + x +1)

Приравниваем коэффициенты :

A +C = 0

A =1;

A −2C + D = 3

=1;

B +C −2D = 0

C = −1;

D = 0.

−A + B + D = 0

Тогда искомое разложение

3x2

−

(x −1)2 (x2 + x +1)

x −1

(x −1)2

x2 + x +1

В результате изучения материала, изложенного в этих лекциях, у студентов должны сформироваться следующие понятия:

комплексные числа и формы их записи,

действия над комплексными числами,

многочлены в комплексной области. Студент должен уметь:

преобразовывать комплексные числа из одной формы в другую,

сравнивать, складывать, вычитать, умножать, делить комплексные числа, возводить в целую степень, извлекать корни целых степеней в удобной для каждого действия форме;

разлагать рациональные дроби на сумму элементарных.

Лекции 5 - 6 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Интегральное исчисление возникло из потребности создать общий метод разыскания площадей, объемов и центров тяжести. В зародышевой форме такой метод применялся еще Архимедом. Систематическое развитие он получил в 17-м веке, в тесной связи с возникшим тогда же дифференциальным исчислением. В данных лекциях рассматривается первая часть задачи – вычисление первообразной как операция, обратная дифференцированию.

5.1.Основные определения

5.2.Свойства неопределенного интеграла

5.3.Таблица основных интегралов

5.4.Методы интегрирования

5.4.1.Непосредственное интегрирование

5.4.2.Замена переменной в неопределенном интеграле

5.4.3.Интегрирование по частям

5.4.4.Возвратное интегрирование

6.1.Интегрирование рациональных дробей

6.1.1.Интегрирование простейших дробей

6.1.2.Общая схема интегрирования рациональной дроби

6.2.Интегрирование выражений, содержащих тригонометрические функции

6.2.1.Интегралы, содержащие произведение

тригонометрических функций вида ∫sinm xcosn xdx . 6.2.2. Интегралы вида ∫cosαxcosβxdx;

∫cosαx sinβxdx; ∫sinαxsinβxdx.

6.3.Интегрирование иррациональных выражений

6.3.1.Линейные иррациональности

6.3.2.Дробно-линейные иррациональности

6.3.3.Квадратичные иррациональности - тригонометрические подстановки

6.3.4.Интегрирование дифференциальных биномов

6.3.5.Метод неопределенных коэффициентов

для интегрирования иррациональностей 6.3.6. Подстановки Эйлера

Неопределенный интеграл

219

5.1. Основные определения

ОФункция F (x) называется первообразной для функции f (x) на интервале (a, b), если F (x) дифференцируема на (a, b) и F′(x) = f (x) .

Пример:

F (x)= x2	f (x)=2x, (-∞,∞) ,
F (x)= sin x	f (x)=cos(x), (-∞,∞) ,
F (x)= x	f (x)= =	1	, (0, ∞)

	2	x

ТЕсли F1 (x) и F2 (x) – две первообразные для функции f (x) на интервале (a, b), то они могут отличаться лишь на постоянную,

т.е. F1 (x)= F2 (x)+ C , где C – постоянная. Доказательство:

Положим Φ (x)= F1 (x)− F2 (x).

Φ′(x)= F1′(x)− F2′(x)= f (x)− f (x)= 0 , следовательно, по теореме Лагранжа Φ (x)= C .

(F (x)+C)′ = F′(x)+C′ = f (x)+ 0 = f (x).

CЕсли F (x) – одна из первообразных для функции f (x), то любая ее первообразная имеет вид: Φ(x)= F (x)+ C , где C – постоянная.

ОСовокупность всех первообразных для функции f (x) на интервале

(a, b) называется неопределенным интегралом от функции f (x) и

обозначается символом ∫ f (x)dx , где ∫ – знак интеграла, f (x) – подынтегральная функция, f (x)dx – подынтегральное выражение.

ТТеорема об интегрируемости непрерывных и монотонных функций

Если f (x)- непрерывна или кусочно-монотонна на [a,b], то она интегрируема на [a,b].

220	Лекции 5 - 6

5.2. Свойства неопределенного интеграла

Из определения следует, что неопределенный интеграл обладает следующими свойствами:

1)dF (x) = f (x) dx ;

2)∫dF (x)= F (x)+ C ;

3)	∫		∫	f (x) dx			, где C – постоянная;
3)	Cf	(x) dx = C		f (x) dx			, где C – постоянная;
4)	f (x)± g (x) dx =				∫	f (x)	dx ±	∫	g (x) dx ;
	∫				∫			∫
5)	Если	∫ f (x)dx = F (x) + C , то ∫ f (ax + b)dx = 1F (ax + b)								+ C .
									a

(Доказательство свойства 5 проведем позднее).

5.3. Таблица основных интегралов

∫0dx = С, ∫dx = x +C

∫xα dx =	xα+1	+C ( α ≠ -1)
	α +1

∫x-1dx = ∫dxx = ln x + C

∫axdx = ax + C, a >0, a ≠ 1 ln a

∫exdx = ex + C

∫sin xdx = −cos x +C

∫cos xdx = sin x + C

∫cosdx2 x = tg x +C

∫sindx2 x = −ctg x +C

∫

= arcsin

+C,

a2 − x2

∫

= ln

x + x2 − a2

x2 − a2

= ln (x + x2 + a2 )+ C

∫

+ a

∫a2 dx+ x2 = 1a arctg ax + C (a ≠ 0)

∫shx dx = chx + C

∫chx dx = shx + C

∫chdx2 x = thx +C

∫shdx2 x = −cthx +C

∫		dx		=	1	ln	x + a	+C

	a	2	2		2a		x − a
		− x

Неопределенный интеграл

221

!Производная любой элементарной функции сама является элементарной функцией. Интегралы от некоторых элементарных функций не выражаются через элементарные функции, они называются неберущимися.

Пример:

∫e−x 2 dx – неберущийся интеграл.

5.4.Методы интегрирования

5.4.1. Непосредственное интегрирование

Отыскание неопределенных интегралов с помощью свойств интегралов, таблицы интегралов и алгебраических преобразований подынтегральной функции называется непосредственным интегрированием.

Пример:

∫2

2 x

)

dx = ∫(2250)

dx =

(2250)x

dx = ∫(2 3

ln 2250

+ C

2) ∫(x5 + x7 +8 x )dx =

8x3/ 2

+C =

16x3/ 2

+C.

3/ 2

5.4.2. Замена переменной в неопределенном интеграле

ТПусть функция x =ϕ(t ) определена и дифференцируема на некотором множестве {t} и пусть {x} – множество всех значений этой функции. Пусть для функции f (x) существует на множестве {x} первообразная функция F (x), т.е. ∫ f (x)dx = F (x)+ C . Тогда всюду на множестве {t}

для функции

f ϕ(t ) ϕ′(t )

существует первообразная функция, равная

(

))

∫

(

)

(

))

, т.е.

)

ϕ′

dt = F

+ C .

f ϕ

Доказательство:

Пусть F′(x)= f (x), ∫ f (x)dx = F (x)+C . По правилу дифференцирова-

ния

сложной

функции

F ϕ(t )

dF (x)

= f ϕ(t ) ϕ′(t ), значит,

∫

(

)

(

)

(

dx dt

ϕ′

dt = F

))

+ C , что и требовалось доказать.

f ϕ

222

Лекции 5 - 6

Пример:

Пусть ∫ f (t )dt = F (t )+C .

∫

f (ax)dx = t = ax, x

, dx =

∫ f (t )dt =

= 1

F (t )+C = 1 F

(ax)+C ,

t = x +b,

∫

=∫ f (t )dt = F (t )+C = F (x +b)+C ,

f (x +b)dx = x

= t −b,

dx = dt

= ax +b,

∫

f (ax +b)dx = x =

−

= ∫ f (t )

F (t )+C =

F (ax

+b)+C .

dx =

Пример:

1). ∫sin (8x − 2)dx = −

1 cos (8x − 2)+ C ;

t =

x −1,

x = t2 +1,

=∫

(t2

+1) t 2t dt =

∫x x −1dx =

dx =

2t dt

= 2∫(t4 +t2 )dt = 2 t5 +

2 t3

+C =

(x −1)5 + 2

(x −1)3 +C .

x = 2t,

3)∫ dx = 1 ∫ dx = ∫ dt = tg t

1+ cos x 2 cos2 2x cos2 t

!Частным случаем замены является преобразование подынтегральной функции, связанное с подведением под знак дифференциала части подынтегральной функции.

Вэтом случае замена носит характер переобозначения.= =t 2dx = 2dt + C = tg 2x + C .,x

Пример:

1)		xdx	=		12 d (x2 +1)	=	t = x2	+1 =
	∫ x2 +1			∫	x2 +1
							{	}

= 12 ∫dtt = 12 ln t +C = 12 ln (1+ x2 )+C .

Неопределенный интеграл

223

2) ∫

= ∫(5x −2)−1/ 2 dx = 1 ∫(5x −2)−1/ 2 d(5x −2)=

5x −2

={t = 5x − 2}= 1 ∫t−1/ 2dt = 1

t1 / 2

+C = 2

5x − 2 + C .

5 1/ 2

3) ∫

sin x cos xdx =∫

sin xd sin x = {t = sin x} = ∫t 2 dt =

+C =

= 2 (sin x)2

+C .

Дополнительные примеры:

Пример:

sin x

= cos x

∫tg x dx = ∫

dx =

= −∫

= −ln

+C = −ln

cosx

+C .

cos x

du = −sin x dx

Пример:

t = 1 − x, x = 1 −t,

∫(2x +3)

(1 − x)

dx = −dt,

= −∫(5 −2t )

t8 dt =

2x +3 = −2t + 5

=−∫(25t8 −20t9 +4t10 )dt = − 259 t9 + 1020 t10 − 114 t11 =

=− 259 (1 − x)9 + 2 (1 − x)10 − 114 (1 − x)11 +C .

Пример:

t = x +

∫sin x + cos x

∫

sin

dt = dx

x +

+C =

+C .

Пример:

∫1 − sinx

x = ∫ 1x

dx − ∫ sin x x dx .

1 )

2 )

1) ∫

1 dx = ∫x−1/ 2dx = x1/ 2

+C ;

1/ 2

sin

x = t,

2) ∫

dx =

= ∫sin t 2dt = 2cost + C = 2 cos x + C .

∫

1−sin

x dx = 2 x + 2cos

x +C .

224

Лекции 5 - 6

Пример:

+ e

t = e

∫

dx = ∫

dx =

1−e

dt = e

= ∫

dt = −∫ 1+

dt = −{t + 2ln

−1

}+C = = −e x − 2 ln

e x −1

+C .

−t

t −1

Пример:

t = ln (tg x),

ln (tg

1 dx

dx =

∫ sin 2x

cos2 x

sin x cos x

2dx

= 1 dt

sin 2x

1∫t dt = t2 +C = 1 ln2 tg x +C .

24 4

Пример:

∫ cos x dx

= sin x,

= ∫

esin x −1

= cos x dx

et −1

домножим и разделим числитель

= 2∫

и знаменатель на e

и на

2et

−1

u =

−1

= u2 +1,

dt = 2∫

= 2∫

2 et

−1

= 2arctgu +C =

du =

−1

= 2arctg esin x −1 +C .

Пример:

ln(arccos x)dx

t = ln(arccos x)

∫ 1− x2 arccos x

dt = arccos x

−

1− x

= −∫t dt = −

+ C = −

1 ln2

(arccos x)+ C .

5.4.3. Интегрирование по частям

d (u v)= (u v)′dx = (u 'v + v'u)dx = u 'vdx + v'udx = vdu +udv ; d (uv)= udv + vdu ; udv = d (uv)− vdu ; ∫udv = ∫d (uv)− ∫vdu ;

∫udv = uv − ∫vdu - формула интегрирования по частям.

Неопределенный интеграл

225

Эта формула используется в тех случаях, когда новый интеграл проще исходного.

1. В интегралах вида ∫Pk (x)ex dx ; ∫Pk (x)sin x dx ; ∫Pk (x)cos x dx за u обозначается многочлен порядка k Pk (x) ;

Пример:
u = x	dv = sin xdx
∫x sin xdx =
du = dx v = −cos x

=-x cos x + ∫cos xdx = −x cos x +sin x +C .

!Формулу интегрирования по частям можно применять повторно.

Пример:

∫x2 cos x dx = u = x

dv = cos x dx

du = 2xdx

v = sin x

= x2 sin x − 2∫xsin x dx =

u = x

dv = sin x dx

= x2 sin x −2 (−x cos x − ∫(−cos x)dx)=

v = −cos x

du = dx

= x2 sin x + 2x cos x −2sin x +C .

Пример:

u = x dv

= dx 2x

x 2x dx =

x 2

−

dx =

x 2

−

+C .

∫

du = dx

v =

ln2

(ln2)2

ln2

Пример:

∫x sh x dx =

u = x

dv = sh x dx

= x ch x − ∫ch x dx = x ch x −sh x +C .

v = ch x

du = dx

2. В интегралах вида ∫Pk (x)ln x dx ,

∫Pk (x)arcsin x dx ,

∫Pk (x)arccos x dx ,

∫Pk ( x )arctg xdx , ∫Pk ( x )arcctg xdx за u обозначается логарифм или обратная тригонометрическая функция.

Пример:
		u	= arctg x, dv					= dx
					dx				=
	∫arctg x dx =				dx				=
		du =					, v = x
		du =		1	+ x	2	, v = x
				1	+ x
	xarctgx − ∫	xdx	= xarctgx − 12 ln (1+ x2 )+C
	xarctgx − ∫	1+ x2	= xarctgx − 12 ln (1+ x2 )+C

226

Лекции 5 - 6

Пример:

= ln(tg x)

dv = sin x dx

∫sin x ln(tg x)dx =

v = −cos x

du =

tg x

cos

= −cos xln(tg x)−∫(−cos x)

= −cos xln(tg x)+ ∫

tg x

cos2 x

sin x

=−cos xln(tg x)+ln tg 2x +C .

5.4.4.Возвратное интегрирование

Так называемое возвратное интегрирование применяется при вычис-

лении интегралов вида:

∫eax cosbx dx ,

∫eax sin bx dx ,

∫cos(ln x)dx ,

∫sin (ln x)dx

и подобных.

Пример:

∫eax sin bx

dx .

Обозначим I = ∫eax sin bx dx . Тогда

u = e

dv = sin bx dx

∫

eax sin bx dx =

cos bx

du = ae

v = −

∫e

= −

cos bx +

cos bx dx = −

cos bx +

I1 .

Полученный интеграл I1

возьмем по частям:

u = e

dv = cos bx dx

∫

cos bx dx =

= −

cos bx +

sin bx

du = aeax dx

v =

sin bx

ax sin bx

−

sin bx dx

= −

cos bx +

−

I .

b ∫

То есть

I = −

cosbx

sin bx

−

I . Выразим отсюда искомый

интеграл I : ∫eax sin bx dx =

eax (asin bx

−bcosbx)

+C .

a2 +b2

6.1. Интегрирование рациональных дробей

ОРациональной дробью называется отношение двух алгебраических многочленов


Неопределенный интеграл									227
	P (x)			b xm + b xm−1		+... + b		x + b
	m		=	0	1	m−1		m		.
	R	(x)		a	xn + a xn−1	+... + a	n−1	x + a	n
	n			0	1		n−1		n

6.1.1. Интегрирование простейших дробей

ОПравильные дроби четырех типов:

1) x −Aa ;

2) (x − a)k , где k – целое положительное число, k >1,

Ax + B

3) x2 + px + q ;

Ax + B

4) (x2 + px + q)k , где x2 + px + q – квадратный трехчлен

с отрицательным дискриминантом p2 − q < 0 ,

называют простейшими дробями.

Методы интегрирования простейших дробей

∫

Adx

= A∫

d (x − a)

= Aln

x − a

+ C ;

x − a

∫

Adx

=Aln

x − a

+ C .

x − a

(x − a)−n+1

∫

Adx

A∫(x − a)

−n

d (x − a)

= A

−n +1 + C =

+ C ;

(x − a)n

(1 − n)

(x − a)n−1

∫

Adx

+ C .

(x − a)n

1 − n

(x − a)n−1

Для вычисления интеграла ∫

Ax + B

разобьем его на два интегра-

x2 + px + q

ла, первый из которых Ia в числителе содержит дифференциал знамена-

теля, а второй Ib

не содержит x в числителе.

Обозначим u = x2 + px + q du = (2x + p)dx .

∫

Ax + B

2x + p

B − Ap / 2

dx =

∫

+ ∫

dx ;

x2 + px + q

+ px + q

x2 + px + q

228

Лекции 5 - 6

+C =

x2 + px + q

+C ,

∫

= B

−

+ px +

+ q −

Здесь мы выделили полный квадрат в знаменателе и учли, что q −

> 0 .

t = x + p / 2,

Сделаем замену переменной

dt = dx,

= q − p2 / 4 .

тогда

B − Ap / 2

x + p / 2

Ib =

B −

arctg

+ C .

∫t

+ a

q − p2 / 4

4. Рассмотрим интеграл ∫

Ax + B

dx .

+ px + q)

Аналогично тому, как это было сделано для интеграла 3, заменим

u = x2 + px + q du = (2x + p)dx .

Разобьем интеграл на два интеграла:

∫

Ax + B

dx =

∫

2x + p

dx + ∫

(B − Ap / 2)

dx .

(x2 + px + q)k

(x2

+ px + q)k

(x2

+ px

+ q)k

u−k +1

Ia =

∫uk

+ C = −

+ C .

(1 − k )

(k −1)(x2 + px + q)k −1

t = x + p / 2,

∫

Ib = B −

(

)

+ px + q

q − p

/ 4

= B

−

B −

, где

Ik =

∫(t2 + a2 )

Неопределенный интеграл

229

Вычислим

Ik = ∫(t2 +dta2 )k

Имеем

u =

dv = dt

+ a

)

+ a

) −a

+ 2k

dt =

-k2tdt

(t2

+ a2 )k

∫ (t

2 + a2 )k +1

v = t

+ a

)

k +1

+ 2k

∫

− 2ka

∫

(t2 + a2 )k

(t2 + a2 )k +1

Ik = (t2 +ta2 )k + 2kIk − 2ka2 Ik+1 ;

Ik +1 =	t	+	2k −1 Ik .
	2ka2 (t2 + a2 )k
			2ka2

Получена рекуррентная (возвратная) формула, выражающая значение инте-

грала от k +1 -

й степени через значение интеграла от k

- й степени. Зная

I =

= 1 arctg

+ C , по формуле можно найти I

, затем, используя I

∫t2

+ a2

найти I3 и т.д.

Пример:

∫

x −1

dx .

x2 + x +1

Правильная дробь типа 3.

x −1

2x +1

−1−1/ 2

∫

dx =

t = x

+ x +1

∫

dx + ∫

dx =

+ x +1

= (2x +1)dx

∫

−

∫

x2 + x +1

= 1 ln

+C = 1 ln

+ x +1

+C ,

v = x +1/ 2,

= −

∫v2 + ( 3 / 2)2

2 ∫(x +1/ 2)2 +3/ 4 dv = dx

= − 3

arctg

(x +1/ 2) 2 +C .

2x +1

Ответ:

1 ln x2 + x +1 −

3arctg

+C .

230	Лекции 5 - 6

6.1.2. Общая схема интегрирования рациональной дроби ∫Pm (z) dz Pn (z)

1. Если дробь Pm ( z ) неправильная ( m ≥ n ), то путем деления числителя на

Pn( z )

знаменатель получают многочлен и правильную рациональную дробь.

P ( z )	= Ql	( z ) +	Rp	( z )	, где Ql	( z ), Rp ( z )- многочлены степени l и p со-
m

Pn ( z )			Pn ( z )

ответственно;Ql ( z ) - частное (целая часть дроби); l ≤ m, l + n = m Rp ( z ) - остаток ( p<n ).

2.Интегрируют многочлен.

3.Находят корни знаменателя правильной рациональной дроби и разлагают знаменатель на квадратичные и (либо) линейные множители с вещественными коэффициентами.

4.Записывают разложение полученной правильной дроби на простейшие.

5.Интегрируют каждую простейшую дробь.

Вывод: интеграл от рациональной дроби выражается через элементарные функции: рациональные дроби, arctg(t) и ln(t) .

Пример:

Вычислить∫

xdx

(

)

−1 (x − 2)

Решение:

Разлагаем правильную дробь

на сумму простейших:

(

x2 −1 (x −2)

)

;

(

−1 (x −2)

(x-1)

(x +1)

(x − 2)

)

x= A(x +1)(x − 2) + B(x −1)(x − 2) + C(x −1)(x +1) ;

x=1:1 = −2A, A = − 12 ;

x= −1: −1 = B(−2)(−3), B = − 16 ;

x = 2 : 2 = C(1)(3),

C =

2 .

= −

−

(x2 −1)(x −2)

2(x −1)

6(x +1)

3(x − 2)

По свойству линейности:

∫

dx = −

−

(x2 −1)(x − 2)

x −1

x +1

x − 2

= − 1 ln

x −1

− 1 ln

x +

2 ln

x −2

+C .

Пример:

Неопределенный интеграл

231

Вычислить ∫

+ 2x4 + 2x2 −1

dx .

(

x2 +1

)

x6 + 2x4 + 2x2 −1

- неправильная дробь.

(

)

x2 +1 2

Выделим целую часть:

x6 + 2x4 + 2x2 −1

= x

−1

x(x2 +1)2

x(x2

1)2

Разложим правильную дробь на сумму простейших

x2 -1

B x + D

x(x2 +1)2

= x

(x2

+1)2 .

x2 -1 = A(x2 +1)2 + x(x2 +1) (B x + D ) + x(B x + D ) ;

x = 0 : −1 = A;

x4 : Ax4 + B x4 =

0, A + B

0, B =1;

x3 : D = 0;

x2 : 2A + B + B

=1, B

x : D1 + D2 = 0, D2 = 0;

x2 -1

;

= − x +

x(x2 +1)2

(x2 +1)

(x2 +1)2

∫

+ 2x4 + 2x2 −1

(

)

= ∫xdx − ∫dxx + ∫

dx + 2∫

dx =

(x2 +1)

(

)

−ln

∫

d (x2 +1)

∫

d (x2 +1)

(x2 +1)

(x2 +1)2

−ln

ln (x2 +1)−

+C .

(

)

232	Лекции 5 - 6

6.2.Интегрирование выражений, содержащих тригонометрические функции

6.2.1.Интегралы, содержащие произведение тригонометрических функций вида ∫sinm xcosn xdx .

1.Пусть n и m - четные, неотрицательные числа. m = 2k , n = 2l, k, l Ν. В

подынтегральной функции степени понижаются посредством перехода к двойному аргументу:

cos2 x =

1 + cos 2x , sin2 x = 1 −cos 2x ;

1 sin 2x .

sin xcos x =

Пример:

1+cos 2x 2

∫

cos xdx =

∫

dx =

cos 2xdx +

cos 2xdx =

sin 2x +

∫(1+cos 4x)dx =

sin 2x +

sin 4x +C .

Пример:

∫sin 2

x cos 4

xdx = ∫(sin x cos x)2 cos2

xdx =

= ∫

sin 2 2x (1 + cos 2x)

∫sin

2xdx +

∫sin

2x cos 2xdx =

∫

1 −cos 4x dx =

− sin 4x + C .

∫

sin 2 2xd(sin 2x) =

sin3 2x + C .

=16x − sin644x + 481 sin3 2x +C .

2.Пусть хотя бы одно из чисел n и m - нечетное положительное.

От нечетной степени отщепляется один сомножитель и заносится под

знак дифференциала d, а оставшаяся подынтегральная функция выражается через функцию, стоящую под знаком дифференциала по формуле sin2 x + cos2 x =1 .

	Неопределенный интеграл	233
	Пример:
	∫sin3 x cos5 xdx = ∫sin3 x cos4 x cos xdx =

=∫sin3 x cos4 xd sin x =∫sin3 x (1−sin2 x)2 d sin x =

=∫(sin3 x − 2sin5 x +sin7 x)d sin x = 41 sin4 x − 31 sin6 x + 81 sin8 x +C ;

1−cos

d cos x

∫

sin

dx = ∫

sin

x sin xdx

= −∫

(

)

−

+C .

cos

2 cos

3. Пусть n и m - таковы,

что m + n = −2k , где k Ν,

то есть сумма m + n

является четным отрицательным целым. Используется подстановка tgx = t , с

использованием формулы: 1+ tg2 x = cos12 x .

sin

xdx

−5 = −2

sin

x dx

tg3 x d (tg x)= tg

+ C

∫

cos5 x

tgx = t

∫cos3 x cos2 x

∫

6.2.2. Интегралы вида ∫cosαxcosβxdx; ∫cosαxsinβxdx; ∫sinαxsinβxdx.

Для вычисления следует перейти к сумме функций и сумме интегралов:

cosαx cos βx = 21 cos (α − β )x + cos (α + β )x ,

cosαx sin βx = 21 sin(α − β )x + sin(α + β )x ,

sinαx sin βx = 21 [cos (α − β )x − cos (α + β )x ] .

6.2.3. Универсальная тригонометрическая подстановка

Интегралы вида ∫R(sin x, cos x )dx , где R (sin x,cos x)= R(u,v) – рацио-

нальная функция двух переменных, u = sin x,v = cos x , вычисляются с помо-

щью так называемой универсальной тригонометрической подстановки

t = tg	x	. Подстановка	t = tg	x	сводит указанный интеграл к интегралу от
	2
			2

дробно-рациональной функции от одной переменной t .

234

Лекции 5 - 6

Рассмотрим:

2tg

2 sin

cos

2 sin

cos

sin x =

;

2 x

1 +t2

cos

+ sin

cos

1 +tg

1 + tg

2 x

−tg

cos2

−sin

cos

1 −t

cos x =

;

cos

+ sin

2 x

+ tg

1 + t2

cos

x = 2arctgt, dx =

2dt

1 +t2

Формулы универсальной тригонометрической подстановки имеют вид:

dx =

2dt

; sin x =

;cos x

1 −t2

;

tgx =

;

1 + t

+ t2

−t2

∫

R (sin x,cos x)dx =

∫

;1 − t

2dt

+ t

1 + t

Пример:

2dt

= tg

dx =

, sin x =

∫sin x

1+t2

+t2

)

2dt

1+t2

= ∫

(

= ∫

= ln

+C.

(

)

Пример:

					x
		t = tg
		t = tg		2
				2
							1 −t 2
							1 −t 2
	dx	cos x		=			1 + t 2
		=							=
∫4 cos x + 3sin x + 5		=					2t		=
∫4 cos x + 3sin x + 5							2t
		sin x =
		sin x =				1 + t 2
					2dt
					2dt
		dx =
		dx =	1 + t					2
			1 + t

Неопределенный интеграл

235

2dt

= ∫

1 +t2

= ∫

1 −t2

1+ t2

4 − 4t2 +6t +5 +5t2

t2 +6t +9

1 + t2

+ t

1+ t2

= 2∫

+C = −

+C.

= −

(t +3)2

t +3

!Если подынтегральная функция R (sin x, cos x) является четной функци-

ей sin x , cos x , то более эффективной, чем подстановка t = tg 2x , является подстановка t = tgx .

Пример:

∫

= ∫

∫

dtgx

a2 sin2 x +b2 cos2 x

cos2 x (a2 tg2 x +b2 )

x + a2

={t = tgx}=

∫

arctg

+C =

arctg a tgx +C

Вообще говоря, перечисленные методы не исчерпывают всех способов вычисления интегралов от тригонометрических функций.

Пример:

cos x

dx =

sin x = t

∫cos x

∫cos2 x

∫1 −sin 2

dt = cos xdx

1 1+t +(1−t )

1 dt

∫

∫(1+t )(1−t ) dt

∫

−

2 ln

−1

1−t

1+t

1−t2

1 ln

1 + t

+ C =

1 ln

1 + t

+ C =

1 ln

1 + sin x

+ C =

t −1

sin x −1

+ cos

sin

+ C

= ln

+ C.

− cos

sin

∫

= ln

+C.

cos x

236	Лекции 5 - 6

6.3. Интегрирование иррациональных выражений

6.3.1. Линейные иррациональности

Рассмотрим интегралы вида

			m1		m2	mk
∫			n		n	n
∫	R			, (ax +b) 2 ,..., (ax +b)
	R	x, (ax + b) 1		, (ax +b) 2 ,..., (ax +b)		k dx ,

где (ax +b) ni - линейные иррациональности-корни порядка ni, а R(x,y,z,...) - дробно-рациональная функция своих аргументов.

Пусть S – общий знаменатель дробей	m1	,	m2	, ...,	mk	, тогда подстановка
			n
	n				n
	1		2		k

ts = ax + b сводит указанный интеграл к интегралу от дробно-рациональной функции одного аргумента.

Пример:

					(2x -1)																	1				3								4									t4 +1					3
													dx				=							,				, S = 4, t							= 2x				−1 ; x		=					; dx = 2t			dt		=
∫ 4 (2x -1)3 +													dx				=					2		,		4		, S = 4, t							= 2x				−1 ; x		=			2		; dx = 2t			dt		=
∫ 4 (2x -1)3 +												1										2				4																		2
= ∫			t2		2t3dt				=			2∫			t2		(t3 +1 −1)										dt = 2∫t					2	dt		- 2∫		t2 dt			=
= ∫			t		3	+1			=			2∫						t	3		+1						dt = 2∫t						dt		- 2∫		t	3	+1	=
			t			+1												t			+1																t		+1
=		2	t	3		−	2	∫			dt3					=		2		t	3				2			t	3	+1	+ c =					2					3			2			3			+ c .
		2		3			2				dt3							2			3		-		2	ln			3						=	2		(2x -1)			4	−		2	ln	(2x -1)4		+1
	3						3			t	3	+		1				3					-	3		ln									=	3		(2x -1)			4	−		3	ln	(2x -1)4		+1
	3						3			t		+		1				3						3												3								3

6.3.2. Дробно-линейные иррациональности

, ... , ax

Интегралы

вида

∫

R x, ax + b n1

+ b nk dx , где

R( x, y,...) –

cx + d

+ d

дробно-рациональная функция, вычисляются

при

помощи

подстановки

ax + b = tS

, где S

– общий знаменатель дробей

m1 ,..., mk .

cx + d

Пример:

∫

1+ x

dx =

(1+ x)2

1-x

Неопределенный интеграл

237

1 + x

= t

, 1 + x = t

− xt

x + xt

= t

−1, x(1 + t

)

= t

−1,

1-x

−1

+1 − 2

−2

x =

, x =

, dx =

+ t2

+ t2 )2

1 + t2

= ∫

4tdt

∫

4t2dt

+ t

−1

(1+ t2 )2

(t2 +1+t2 −1)2

4t2dt

1-x

= ∫

= ∫t2

= − t +c = -

+c .

(2t2 )2

1+ x

6.3.3.Квадратичные иррациональности - тригонометрические подстановки

Интегралы вида ∫R(x, ax2 +bx + c )dx , где ax2 + bx + c - квадратичная

иррациональность, а R( u,v ) - дробно-рациональная функция своих аргументов, выделением полного квадрата в квадратном трехчлене и заменой

u = x + 2ba приводятся к интегралу одного из следующих трех типов:

1)∫R (u, l2 −u2 )du ;

2)∫R (u, l2 + u2 )du ;

3)∫R (u, u2 −l2 )du ,

ккоторым применяют тригонометрические подстановки соответственно:

1)u = l sint или u = l tht ,

2)u = l tg t или u = l sht ,

3)u = cosl t или u = l cht ,

после чего подынтегральная функция сводится к тригонометрической.

Пример:

∫ 5 + 2x - x2 dx = ∫ 5 −( x2 − 2x)dx = ∫ 5 - ( x -1)2 +1 dx = ∫ 6 - ( x -1)2 dx =

x -1 = u		∫ 6 - u2 du =
=	=	∫ 6 - u2 du =
dx = du
					u
= u = 6 sin		t	, du = 6 cos t dt ;	t = arcsin		=
= u = 6 sin		t	, du = 6 cos t dt ;	t = arcsin	6	=
					6
= ∫	6 - 6 sin2 t		6 cos t dt = 6∫	cos2 t dt =	6 ∫(1 + cos 2t)dt =
					2

238

Лекции 5 - 6

= 3t

sin

2t + c =

3 arcsin

x -1

sin 2arcsin

x -1

+ c =

x -1

= 3arcsin

sin 2α + c = {sin 2α = 2 sin α cos α} =

x -1

(x -1)2

= 3arcsin

−

+ c .

Частные случаи квадратичных иррациональностей

Интегралы вида ∫

выделением полного квадрата в знаме-

+ bx + c

нателе сводятся к табличным.

Пример:

∫

+ 2x +

+ 2x +1+ 4

= ∫

d (x +1)

= ln

x +1

+ 2x +5

+ c

( x +1)

Для интегралов вида

∫

Ax + B

в числителе выделяется произ-

+ bx + c

водная квадратного трехчлена, стоящего в знаменателе, и интеграл сво-

дится к табличному, либо рассмотренному ранее.

Пример:

∫

5x - 3

dx =

2x2 +8x +1

5 (4x +8) -13

(4x +8)dx

= ∫

dx =

∫

-13∫

2x2 +8x +1

∫

d (2x2 +8x +1)

−

∫

2x +8x

x2 + 4x +

+ 4 −4

2 2x2 +

8x +1 −

∫

d (x + 2)

(x + 2)2 −

2 2x2 +8x +1 −

4x +

+ c .

x + 2 + x2 +

Неопределенный интеграл

239

Пример:

x = atg t,

dx = a

cos

∫(x2 + a2 )3 / 2

cos2 t

∫

+ a

cos

∫cos t dt

sint +C = ={возвращаемся к старой переменной} =

tg t

+c =

+c .

1+tg 2t

a2 a2 + x2

Интегралы

вида

где

k ≤ 2 , подстановкой

∫(x − a)k

ax2 + bx + c

x − a = 1t ; dx = −t12 dt приводятся к предыдущему случаю.

Пример:

-1

x =

; dx =

dt; t =

∫ x x2 +1

= ∫

= −∫

+ c =

= −ln

t + 1+t2

1+t

1+t2

−ln

1 +

+ c .

6.3.4. Интегрирование дифференциальных биномов

Выражение вида xm (a +bxn )p dx , где m,n, p - рациональные дроби, a,b − const , называется дифференциальным биномом.

ТИнтеграл от дифференциального бинома приводится к интегралу от рациональной функции в трех случаях подстановками Чебышева. В остальных случаях интеграл не вычисляется через элементарные функции. Случай 1: p - целое число.

240			Лекции 5 - 6
Используется подстановка x = ts , где s –			НОК знаменателей дробей
m и n (НОК - наименьшее общее кратное).
Случай 2:	m +1	- целое число.
Случай 2:		- целое число.
	n

Используется подстановка a + bxn = ts , где s – знаменатель дроби p .

Случай 3: mn+1 + p - целое число.

Используется подстановка ax−n + b = ts , где s – знаменатель дроби p .

Пример:

∫

= ∫x−1

(1 + x2 )−

1 .

2 dx , m = −1, n = 2, p = −

m +1

= 0 - целое - случай 2, используется замена

1 + x2

= t2 , x2 = t2

−1, x = t2 −1,

dx =

2tdt

t2 −1

∫

t dt

∫

= −∫

t +1

+c =

= − 2 ln

t −1

t2 −1 t2 −1 t

t2 −1

1−t2

= ln

−

+c = ln

x2 +1 −1

+c.

x2 +1 +1

6.3.5.Метод неопределенных коэффициентов для интегрирования иррациональностей

В общем случае интегралы вида ∫				Pn (x)				можно вычислить, ис-
В общем случае интегралы вида ∫				ax	2			можно вычислить, ис-
пользуя следующую формулу:				ax		+ bx + c
пользуя следующую формулу:
	Pn (x)	dx = Q	(x) ax2	+ bx	+ c + λ			dx	,
∫		dx = Q	(x) ax2	+ bx	+ c + λ		∫ ax2 + bx + c		,
	ax2 + bx + c	n−1
	ax2 + bx + c

где Qn−1 (x) - многочлен степени n-1 с коэффициентами, подлежащими определению. Число λ и неопределенные коэффициенты многочлена Qn−1 (x) находятся дифференцированием вышеприведенной формулы.

Пример:

∫			x2	dx = ( Ax + B) x2 + x +1 + λ∫		dx	.
	x	2	+ x +1		x	2
						+ x +1

Дифференцируем по х

Неопределенный интеграл

241

= A x2 + x +1 +

( Ax + B) (2x +1)

+ λ

x2 + x +

+ x +1

2 x2 + x +1

Находим неопределенные коэффициенты.

= A(x

+ x +1)+( Ax

+ B)

+λ .

x2 : 2 A =1; x : A + B +

= 0; x0 : A +

+ λ = 0,

A =

, B = −

= −

, λ = −1 .

x2dx

−

+ x +1 −

∫ x2 + x +1

8 ∫

x2 + x +1

x −

+ x +1 −

x +

+ x +1

+ C .

, где k – любое, подстановкой

Интегралы виды

∫(x − a)k

x − a = 1 , dx = −

ax2 + bx + c

приводятся к предыдущему случаю.

Пример:

∫

−1 =

; dx = −

(x −

+3x +1

= −∫

t3dt

= − ∫

t2dt

+ t

1 + t

+ 5t

+ 3

+5t +1 +

= −

−

∫ 5t2 +5t +1

6.3.6. Подстановки Эйлера

В общем случае интегралы вида

∫R(x,

ax2 +bx+c)dx

можно вычис-

лить, используя подстановки Эйлера.

Указанные подстановки классифицируются по виду коэффициентов a, b, c. Предполагается, что квадратный трехчлен не имеет равных действительных корней, так что корень из него не может быть заменен рациональным выражением.

242

Лекции 5 - 6

Первая подстановка Эйлера: a > 0

Используется замена

ax2 + bx + c = t ±

ax .

Выберем

для

определенности знак

Возведем

в квадрат и

выразим

x =

t2 − c

. Поскольку x -

рациональная функция от t, то dx и t +

ax есть

b − 2t

также рациональные функции от t.

Пример:

∫

; x2 +1 = x + t; x2 +1 = x2 + 2xt + t2 ,

x2 +1

−t2

+ t

x =

−

;

dx =

−

dt = −

dt ,

x2 +1 =

1−t2

1−t2 + 2t2

1+t2 .

1+t

−∫

= −∫

= −ln

=ln

+ c .

1+t2

x2 +1 − x

Избавимся от иррациональности в знаменателе дроби под знаком лога-

рифма, умножив числитель и знаменатель на выражение

x2 +1 + x , то-

гда: ln

= ln

x2 +1 + x

= ln (

+1 + x).

− x

( x2 +1)

− x2

Вторая подстановка Эйлера: c>0

Используется замена

ax2 + bx + c = xt ± c . Выберем для определенно-

сти знак «+».

Пример:

∫

; 1 + x2 = xt +1, 1+ x2 = x2t2 + 2xt +1; x2 = x2t2 + 2xt; x = xt2 + 2t ,

1 + x2

x =

; dx =

2(1 −t2 )+ 2t 2t

2 − 2t2 + 4t2

dt =

2(1 + t2 )

dt ,

1 −t 2

(

)

(

)

(

)

1 −t

1+ x2 =

t 2t

+1 =

2t2 +1−t2

1+t2

1−t2

∫

= ∫

2 (1+t2 )dt

= 2∫

= ln

t +1

1+ x

(1−t

)

2 (1+t

)

−t

t −1

(1−t2 )

Неопределенный интеграл

243

x2 +1

−1

x2 +1 −1+ x

= ln

x2 +1

−1

x2 +1 −1− x

Третья подстановка Эйлера

В этом случае квадратный трехчлен имеет действительные корни α и β .

Используется замена

ax2 + bx + c = (x −α)t .

Пример:

∫

; x2 −1 = (x −1)(x +1), x2 −1 = (x −1)t ,

x2 −1

(x −1)(x +1)= (x −1)2 t2 , (x +1)= (x −1)t2 ,

t2 =

x +1

;t =

x +1

; x +1 = xt2

−t2 ,

x −1

x =

t2 +1

;dx =

2t (t2 −1)−2 (t2 +1)

dt = −

dt ,

(

)

t2 −1

(

)

−

−1

x2 −1 =(x −1)t =

t2 +1 −1 t =

−1

−4t

(

t2 −1

∫

=∫

)

=−2∫

=2∫

x2 −1

t2 −1

1−t2

(

)

t2 −1

t +1

x +1

x +1 + x −1

= ln

x −1

= ln

t −1

x +1

−1

x +1 − x −

x −1

x −1+2 x2 −1 + x +1

(x + x2 −1)

x +

−1

+c .

= ln

x +1− x +1

!На самом деле во всех возможных случаях достаточны первая и третья подстановки. Действительно, если квадратный трехчлен имеет действительные корни, то применима третья подстановка. Если действительных

корней нет, т.е. дискриминант

b2 −4ac <0 , то трехчлен

244			Лекции 5 - 6
ax2 + bx + c =	1	(( ax + b )2 −( b2 − 4ac ))	при всех значениях x имеет знак a.
	4a

Случай a<0 нас не интересует, так как радикал в этом случае вовсе не имеет вещественных значений, значит проходит первая подстановка для a>0.

В результате изучения материала, изложенного в этих лекциях, студенты должны знать:

таблицу основных интегралов;

основные методы интегрирования (непосредственное интегрирование, замена переменной, интегрирование по частям).

Студент должен уметь:

вычислять интегралы от основных типов функций (рациональные дроби, выражения, содержащие тригонометрические функции, иррациональные выражения).

Лекции 7 - 8 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Развитая в прошлой лекции техника вычисления первообразных находит конкретные геометрические и механические приложения в виде определенного интеграла, вычисление которого через основную формулу интегрального исчисления (формулу Ньютона – Лейбница) сводится к вычислению первообразных.

7.1.Определенный интеграл и его свойства/ Основные определения

7.2.Геометрический смысл определенного интеграла

7.3.Теоремы существования

7.4.Свойства определенного интеграла

7.5.Формула Ньютона-Лейбница

7.6.Замена переменной в определенном интеграле

7.6.1.Интегралы от четных и нечетных функций

7.7.Интегрирование по частям

8.1.Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур

8.1.1.Вычисление площади в прямоугольных координатах

8.1.2.Параметрическое задание линий

8.1.3.Вычисление площадей, фигур, граница которых задана кривыми в параметрической форме

8.1.4.Полярные координаты на плоскости

8.1.5.Связь полярных координат с декартовыми

8.1.6.Примеры уравнений линий в полярной системе координат

8.1.7.Площадь криволинейного сектора в полярной системе координат

8.2.Вычисление длины дуги кривой

8.2.1.Вычисление длины плоской кривой в прямоугольных координатах

8.2.2.Вычисление длины плоской кривой в параметрической форме

8.2.3.Вычисление длины дуги пространственной кривой в параметрической форме

8.2.4.Дифференциал длины дуги кривой

8.2.5.Длина кривой, заданной в полярных координатах

8.2.6.Площадь поверхности вращения

8.3.Вычисление объемов тел

8.3.1.Вычисление объемов по заданным площадям поперечных сечений

8.3.2.Вычисление объемов тел вращения

246	Лекции 7 - 8

7.1.Определенный интеграл и его свойства. Основные определения

ОПусть на [a, b] задана непрерыв-

ная функция f (x). Разобьем [a, b]

на n частей точками деления: a = x0 < x1 < x2 < ... < xn = b .

Обозначим: +x1 = x1 − x0 ,

+x2 = x2 − x1 ,… +xi = xi − xi−1 ….

В каждом из отрезков [xi−1 ,xi ] возьмем по точке ξi [xi−1 ,xi ].

				x
				x
x0ξ1 x1 ...		–	xn−1xn


	Рис. 1.1

Составим сумму: Sn = f (ξ1 )+x1 + f (ξ2 )+x2 +... + f (ξn )+xn = ∑ f (ξi )+xi .

i=1

Геометрически Sn есть алгебраическая сумма площадей прямоугольни-

ков, имеющих основания ∆хi и высоты f (ξi). Sn называют интегральной
суммой для		f (x)	на [a, b].
Sn зависит от способа разбиения [a, b] на отрезки [xi−1 ,xi ]							и от выбора
точек ξi внутри [xi−1 ,xi ].
Каждому разбиению соответствует своя Sn .
Таким	образом,		получается последовательность {Sn} . Обозначим
max+xi	-	наибольшую		из	длин	отрезков разбиения	и устремим
max+xi → 0 .
Если при любых разбиениях [a, b]						таких, что max+xi → 0 , и при любом
			n
выборе точек ξi Sn = ∑ f (ξi )+xi стремится к одному пределу S,								то этот
			i=1				[a, b]
предел называется определенным интегралом от f (x) на							[a, b]	и обо-
значается ∫b		f (x)dx . Таким образом, по определению
	a
		b			n
		∫ f	(x)dx =	lim	∑ f (ξi )+xi ;
		a		max+xi →0 i=1

а называется нижним пределом интеграла, b – верхним пределом.

Если ∫b f (x)dx , то f (x) называется интегрируемой на [a, b].

Определенный интеграл

247

7.2. Геометрический смысл определенного интеграла

Геометрически определённый интеграл ∫b f (x)dx представляет собой ал-

гебраическую сумму площадей фигур, ограниченных графиком функции у =f(х), осью Ох и прямыми х = а и х = b, причем площади, расположенные выше оси Ох, входят со знаком плюс, а площади, расположенные ниже оси Ох, - со знаком минус.

7.3. Теоремы существования

ТЕсли f (x) непрерывна на [a, b], то она интегрируема на [a, b].

ТЕсли f (x) кусочно-непрерывна на [a, b] (имеется конечное число точек разрыва первого рода), то она интегрируема на [a, b].

ТЕсли f (x) монотонна на [a, b], то она интегрируема на [a, b].

	В определении ∫b	f (x)dx
!			пределы удовлетворяют ограничению			a < b .
			пределы удовлетворяют ограничению			a < b .
	a
	Снимем это ограничение.		Если a < b , то ∫b	f (x)dx = −∫a	f (x)dx .	Пусть
			a	b

также ∫a f (x)dx =0 .

Пример:

Вычислить∫b kxdx как предел интегральных сумм.

Решение:

+xi = b −n a =+x ; x0 = a;

x1 = x0 ++x;

x2 = x1 ++x = x0 + 2+x.

Пусть ξi = xi−1 (левые концы каждого отрезка)

ξ1 = x0 ; ξ2		= x1 и так далее.				= k (b − a)∑xi −1 =
Sn	= ∑ f (ξi )+xi		= ∑kxi −1 b − a			= k (b − a)∑xi −1 =
	n		n					n
	i =1		i =1		n		n	i =1
	k (b − a)			(b − a)
=		∑ a	+ (i −1)			=
=	n	∑ a	+ (i −1)	n		=
	n	i		n

248	Лекции 7 - 8

	k (b − a)			(b −
=		∑a +
=	n	∑a +		n
	n		i	n

= k (b − a){an2 + bn2 − n 2n

Пусть n → ∞(+x → 0)

∑(i

k (b − a)

(b − a) n (n −1)

−

na +

(b − a)n}.

= k

(

)

kxdx = k

(

)

, lim S

−a2

∫

−a2

n→∞

7.4. Свойства определенного интеграла

1.Независимость величины интеграла от обозначения переменной интег-

рирования: ∫b f (x)dx = ∫b f (t )dt .

2.Линейность определенного интеграла. Если f1 и f2 интегрируемы на [a,b] и А, В – произвольные числа, то

∫b [Af1 + Bf2 ]dx = A∫b

f1dx + B∫b

f2dx .

Доказательство:

Для интеграла в левой части

(ξ

)+ Bf

(ξ

) +x =

∑

i=1

= ∑Af1 (ξi )+xi + ∑Bf2 (ξi )+xi =

i=1

(ξi )+xi .

= A∑ f1

(ξi )+xi + B∑ f2

i=1

По условию

∑ f1

(ξi

)+xi → ∫ f1 (x)dx ,

∑ f2

(ξi )+xi

→

∫ f2 (x)dx .

i=1

f1dx + B

f2dx

Таким образом,

lim

правой части A

∫

lim

ле-

max+xi →0

вой части ∫b [Af1 + Bf2 ]dx = A∫b f1dx + B∫b f2dx , что и требовалось доказать.

3.Аддитивность (разбиение промежутка интегрирования на части). Для любых трех чисел a , b , c справедливо равенство:

∫b f (x)dx = ∫c f (x)dx + ∫b f (x)dx

при условии, что все три интеграла существуют.

Определенный интеграл											249
Доказательство:					b
			b		b	где c - точка деления [a, b].
Пусть a < c < b . Составим ∑ для ∫						где c - точка деления [a, b].
			a		a
c	c		b				b		b	c	b
∑ соответствует	∫	; ∑ соответствует ∫						, ∑ =		∑	+ ∑ перей-
a	a		c				c		a	a	c
дем к пределу при max+xi → 0 : ∫b					f (x)dx = ∫c			f	(x)dx + ∫b		f (x)dx .
				a			a			c
Если a < b < c , то ∫c		= ∫b	+ ∫c	; ∫b	= ∫c	− ∫c	= ∫c		+ ∫b .
	a	a	b	a	a	b		a	c

Теоремы об оценке определенного интеграла

ТСохранение интегралом знака функции. Пусть 1) f (x) интегрируема

на [a, b]; 2)

f (x) ≥ 0

для любых x [a,b], тогда ∫b

f (x)dx ≥ 0 .

Доказательство:

= n f

(ξ

)+x

≥ 0 lim S

≥ 0 , то есть

f (x)dx ≥ 0 , что и требовалось

∑

n→∞

∫

i=1

доказать.

Интегрирование неравенств.

Пусть 1)

f (x),

(x)

интегрируемы на [a, b]; 2)

f (x)≥ g (x) для любых

x [a,b], тогда:

∫b

f (x)dx ≥ ∫b g (x)dx .

Доказательство:

f (x)− g (x)≥ 0 ∫b f (x)− g (x) dx ≥ 0 .

			a
		∫b	f (x)dx − ∫b g (x)dx ≥ 0 ∫b		f (x)dx ≥ ∫b g (x)dx
		a	a	a		a
	Теорема об		оценке. Пусть 1)	f (x)		интегрируема	на	[a, b];
Т	Теорема об		оценке. Пусть 1)	f (x)		интегрируема	на	[a, b];
	2) m и M -наименьшее и наибольшее значения функции						f (x),	тогда
	2) m и M -наименьшее и наибольшее значения функции						f (x),	тогда
	m(b − a)≤ ∫b	f (x)dx ≤ M (b − a).
	a

250	Лекции 7 - 8

Доказательство:

Из условия теоремы m ≤ f (x) ≤ M .

Интегрируем неравенство 1:

∫b mdx ≤ ∫b f (x)dx ≤ ∫b Mdx .

Из линейности ∫b mdx = m∫b dx = m(b − a).

ТТеорема о среднем. Если f (x) непрерывна на [a,b], то c [a,b] такая,

что ∫b f (x)dx = (b − a) f (c).

		a
Доказательство:									∫b
Из		теоремы			об	оценке	m ≤	1		f (x)dx ≤ M , то есть

								(b − a) a
1			∫b	f (x)dx = µ ,		где m ≤ µ ≤ M .

	(b − a) a			f (x)
Так как					непрерывна, то она принимает все промежуточные значе-

ния между m и M. Следовательно, при некотором значении с (c [a,b]) f (c)= µ , то есть ∫b f (x)dx = (b − a) f (c).

						a
			f (c)=	1			∫b	f (x)dx		называется средним значением функции
!	Число			1
!	Число
					(b - a) a
					(b - a) a
	f (x)	на отрезке [a, b].
Пример:
Пример:
								1	dx .
			Оценить интеграл ∫						dx .
			Решение:					0	1+ x 4
			Решение:
			Имеем 1 ≤ 1 + х4 ≤ 2 при 0 ≤ х ≤ 1,
			1 ≤	1		≤1,
			2	1+ x 4
			т.е. m = 1 , М = 1, b − а = 1.
				2
			Следовательно,					1	1	dx ≤ 1.
			Следовательно,					1	≤ ∫	dx ≤ 1.
								2	0	1+ x 4

Определенный интеграл

251

Пример:
			1
	Определить знак интеграла ∫x3e x dx , не вычисляя его.
	Решение:		−1
	Решение:	1	0	1
		1	0	1
	Разобьём интеграл на два ∫x3 exdx = ∫x3 exdx + ∫x3 exdx =
		−1	−1	0
	={поменяем в первом интеграле пределы}=
	−1	1
	= − ∫ x3 ехdx + ∫x3 ехdx =
	0	0
	={заменим в первом интеграле х → (−х), тогда:}=
	1	1	1	1
	= − ∫(− x)3 е−х d(−x) + ∫x3 ехdx = − ∫ x3 e−xdx + ∫x3 ехdx =
	0	0	0	0
	1
	= ∫x3 (ex − e−x) dx, на отрезке х [0, 1],			х3 ≥ 0, ех − е−х ≥ 0,
	0
		1
	следовательно, ∫x3 (ex − e−x) dx ≥ 0, т.е. знак интеграла - плюс.
		0

Производная интеграла по верхнему пределу (теорема Барроу)

Рассмотрим некоторый промежуток [a, b], f (x)- функция, интегрируемая на [a, b], d – фиксированная точка из [a,b], х – любая точка из [a, b]. Из интегрируемости f (x) на [a, b] следует интегрируемость f (x) на [d ,x]. Ес-

ли верхний предел меняется, то меняется и значение интеграла ∫x		f (t )dt , т.е.
	d
можно сказать, что на [a, b] задана функция F (x): F (x) = ∫x	f (t )dt .
d

ОФункция F (x) называется интегралом с переменным верхним пределом.

водная от интеграла по переменному верхнему пределу равна результату подстановки значения верхнего предела в подынтегральную функцию f (x).

Доказательство:

По определению производной F′(x)= lim F (x ++x)− F (x)

+x→0 +x

252					Лекции 7 - 8
	x++x		x
F (x ++x)− F (x)= ∫		f (t )dt − ∫ f (t)dt		= {из	свойства аддитивности}=
	d		d
x	x++x	x	x++x
= ∫ f (t )dt + ∫ f (t )dt − ∫ f			(t)dt = ∫ f	(t )dt = f (µ)+x , x < µ < x ++x ,
d	x	d	x
lim	F (x ++x)− F (x)	= lim	f (µ), так	как	µ → x при +x → 0 , то
lim	+x	= lim	f (µ), так	как	µ → x при +x → 0 , то
+x→0	+x	+x→0		f (x).
lim f (µ) = lim f (µ) = f (x) F ′(x) =				f (x).
+x→0	µ→x

ТТеорема Коши. Всякая непрерывная на [a, b] функция f (x) имеет в

этой области первообразную F (x)= ∫x f (t )dt или, так как первообразная

определяется с точностью до константы, F (x)= ∫x f (t )dt + C , C −const .

!(Обобщение теоремы Барроу). Если функции ϕ (x) и ψ (x) дифферен-

цируемы в точке х [a, b]						и f (t )	непрерывна при ϕ(a)≤ t ≤ψ (b), то
	ψ (x)	′	(	)		(	)			.
	∫		(	)		(	)			.
		f (t)dt =	f ψ (x) ψ		′	(x)− f ϕ (x) ϕ		′	(x)
		f (t)dt =	f ψ (x) ψ			(x)− f ϕ (x) ϕ			(x)
ϕ(x)		x

Пример:

I(х) = ∫e−t 2 dt, найти I′(х).

Решение:

Учтём ϕ(х) = 0, т.е. ϕ′(х) = 0, ψ(х) = х2. I′(х) = e −(x2 )2 (х2)′ = 2хe−x4 .

7.5. Формула Ньютона-Лейбница

Т Пусть f (x) непрерывна на [a, b], тогда

∫ f (x)dx = F (b)− F (a)= F (x) ba .

Доказательство:

По теореме Коши из условия непрерывности f (x) следует существова-

ние F (x)= ∫x f (t )dt + C .

Определенный интеграл						253
Положим, x = a		F (a)= ∫a	f (t )dt + C ,		то	есть C = F (a). Положим,
		a
x = b F (b)= ∫b	f (t)dt + F (a) ∫b			f (t )dt = ∫b		f (x)dx = F (b)− F (a), что и
a			a		a

требовалось.

Таким образом, для вычисления определенного интеграла от непрерывной функции f (x) нужно:

1) не обращая внимания на пределы интегрирования найти первообразную F (x) для подынтегральной функции (по правилам вычисления

неопределенного интеграла);

2)вычислить F (b)− F (a).

Пример:

∫b kxdx = k ∫b xdx = k

= k (b2

− a2 ).

π∫sin xdx = −cos x

π0 = −cosπ + cos 0 = 2 .

Пример:

Вычислить ∫

x ln x

Решение:

e2 d(ln x)

∫

= ln

ln x

= ln(ln e ) − ln(ln e) = ln 2

≈ 0,69.

x ln x

ln x

Пример:

Вычислить

∫4

cos

Решение:

π 4

tgx

π∫

cos2 x

= tg

− tg 6

= 1 −

7.6. Замена переменной в определенном интеграле

ТПусть 1) f (x) непрерывна на [a, b]; 2) x = g (t ) - непрерывно дифференцируема на [α, β] ([a,b] - область значений g (t ) при изменении

254	Лекции 7 - 8
t [α,β]); 3) a = g (α ), b = g (β ), тогда ∫b	β
t [α,β]); 3) a = g (α ), b = g (β ), тогда ∫b	f (x)dx = ∫ f (g (t))g′(t )dt - форму-
a	α

ла замены переменной под знаком определенного интеграла. Доказательство:

Левая часть ∫b f (x)dx = F (b)− F (a).

Здесь F (x) = F (g (t )).

Ft′ = Fx′ xt′ = F ′(g (t )) g′(t );

F ′(g (t ))= F ′(x) = f (x) = f (g (t )).

Таким образом, Ft ' = f (g (t )) g' (t ), следовательно, F (g (t )) является первообразной для функции f (g (t )) g' (t ) на [α,β].

Правая часть ∫ f (g (t )) g '(t )dt = F (g (β ))− F (g (α )), то есть

∫ f (g (t )) g '(t )dt = F (b)− F (a). Левая часть равна правой части, что и тре-

бовалось доказать.

Пример:

x = r sin t,

0=r sinα,

α = 0

∫ r2 − x2 dx =

= r cos tdt,

r=r sin β,

= π∫/ 2

r2 −r2 sin2 tr cos tdt = π∫/ 2 r2 cos2 tdt =

π∫/ 2 (1+ cos 2t )dt =

πr2

sin 2t

Пример:

= x =

dx=-

,1=

,α =1,2 =

∫1 x x2 +1

∫1

=ln (t+

t2 +1)

= −∫2

tdt

11 =

ln (1+

2 )-ln

5 .

2 1+t

1+t

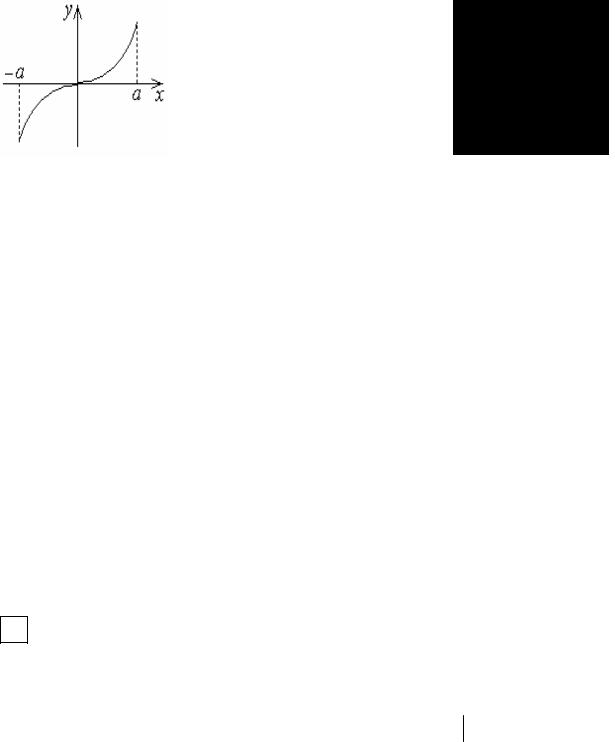
Определенный интеграл			255
7.6.1. Интегралы от четных и нечетных функций на [−a,a]
1) f (x) - четная ( f (−x) = f (x)).
∫a	f (x)dx = ∫0	f (x)dx + ∫a	f (x)dx .
−a	−a	0

∫

−a

x = −t, dx = −dt
		=
f (x)dx =	−a = −α, a = α	=
	0 = −β, β = 0
	0 = −β, β = 0

= −∫0

f (−t )dt = ∫a

f (t )dt = ∫a

f (x)dx ,

∫a

f (x)dx = 2∫a

f (x)dx .

−a

f (x) - нечетная функция

( f (−x) = − f (x)).

∫a

f (x)dx = ∫0

f (x)dx + ∫a

f (x)dx .

−a

x = −t, dx = −dt

∫

f (x)dx = −a = −α, a = α =

−a

0 = −β,

β = 0

= −∫0

f (−t )dt = ∫0

f (t )dt = −∫a

f (x)dx ,

∫a

f (x)dx =0 .

−a

7.7. Интегрирование по частям

Т Пусть u (x) и v (x) имеют на [a, b] непрерывные производные, тогда

b u (x)v′(x)dx = u (x)v (x)	b	− b u′(x)v (x)dx .
b u (x)v′(x)dx = u (x)v (x)	b	− b u′(x)v (x)dx .
∫	a	∫
a		a

Или: так как v '(x)dx = dv , u '(x)dx = du , то ∫b udv = uv

ba − ∫vdu .

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.11.201947.16 Кб2Лекции по бухгалтерской отчетности.doc
#
14.02.2015692.22 Кб33Лекции по ВССиТ.doc
#
16.09.2019877.06 Кб20Лекции по деревянным конструкциям.doc
#
14.02.201539.01 Mб49Лекции по истории.rtf
#
14.02.20152.87 Mб1608Лекции по коллоидной химии.pdf
#
14.02.20159.7 Mб918Лекции по математике.pdf
#
11.09.2019160.26 Кб1Лекции по социологии_на печать.doc
#
03.08.201954.95 Кб13Лекции по статистике.docx
#
14.02.2015147.88 Кб13Лекции по экономике.docx
#
14.02.20156.17 Mб59лекции.doc
#
14.02.20151.07 Mб339ЛЕКЦИи.doc