
Rogozin-fiz2
.pdfW = |
1 |
|
|
∑ qk q'. |
(1.3.11) |
|||
|
|
|
|
|||||
|
4πε0 k |
rk |
|
|||||
Тогда и для потенциала ϕ = ∑ϕk , или |
|
|
||||||
k |
1 |
|
|
|
∑ qk , |
|
||
ϕ = |
|
|
|
(1.3.12) |
||||
|
4πε |
|
|
|
||||
|
|
0 |
|
k |
r |
|
||
|
|
|
|
k |
|
|||
т.е. потенциал поля, создаваемый системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. А вот напряженности складываются при наложении полей – век-
торно. По этой причине потенциалы полей считать проще, чем напряженности.
Вернемся к работе сил электростатического поля над зарядом q. Выразим работу через разность потенциалов между начальной и конеч-
ной точками: |
|
A12 =W1 −W2 = ϕ1q −ϕ2q = q(ϕ1 −ϕ2 ). |
(1.3.13) |
Таким образом, работа над зарядом q равна произведению заряда |
|
на убыль потенциала, т.е. |
|
A = q(ϕ1 −ϕ2 )= qU ; |
|
A = qU , |
(1.3.14) |
где U – напряжение.
Аналогия с гравитационным полем:
A = mgh1 − mgh2 = m(gh1 − gh2 ),
здесь gh – смысл потенциала, а m – заряда гравитационного поля. Итак, потенциал –rскалярная величина, поэтому пользоваться и вы-
числять φ проще, чем E . Приборы для измерения разности потенциалов широко распространены.
Формулу A∞ = qϕ можно использовать для установления единиц
потенциала: за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного положительного заряда необходимо совершить работу, равную единице.
ВСИ единица потенциала 1 В=1 Дж/1Кл.
Вфизике часто используется единица энергии и работы, называе-
мая электрон-вольт (эВ) – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1 В, т.е.
1 эВ =1,6 10−19 Кл В =1,6 10−19 Дж.
31

1.3.4. Связь между напряженностью и потенциалом
Итак, электростатическоеr поле можно описать либо с помощью
векторной величины E , либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее.
Изобразим перемещение заряда q по произвольному пути l
(рис. 1.3.2) в электростатическом поле E .
Работу, совершенную силами электростатического поля на беско-
нечно малом отрезке dl, можно найти так: |
|
dA = Fldl = Elqdl, |
(1.3.15) |
где El – проекция E на dl ; dl – произвольное направление перемещения заряда.
С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем, равна убыли потенциальной энергии заряда,
перемещенного на расстоянии dl: |
|
|
|
|
|
|
|||||
dA = −qdϕ; Elqdl = −qdϕ , |
|
|
|||||||||
отсюда |
|
dϕ |
|
|
|
|
|
|
|
|
|
E = − |
. |
|
|
|
|
|
(1.3.16) |
||||
|
|
|
|
|
|
||||||
l |
|
dl |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
Для ориентации dl (направление перемещения) в пространстве надо |
|||||||||||
знать проекции E на оси координат: |
|
|
|
|
|
||||||
Ex = −∂ϕ; |
Ey = − |
∂ϕ |
; Ez = − |
∂ϕ |
; |
||||||
|
∂x |
|
|
|
∂y |
|
∂z |
|
|||
r |
∂ϕr |
− |
∂ϕr |
∂ϕ r |
|
(1.3.17) |
|||||
E = − |
∂x |
i |
∂y |
j − |
∂z |
k. |
|
||||
|
|
|
|
|
|
|
|
||||
По определению градиента сумма первых производных от какойлибо функции по координатам есть градиент этой функции, т.е.
gradϕ = ∂∂ϕx ri + ∂∂ϕy rj + ∂∂ϕz kr,
grad ϕ – вектор, показывающий направление наибыстрейшего увели-
чения функции. |
|
между E и φ записывается так: |
|
Тогда коротко связьr |
(1.3.18) |
||
|
E |
= −gradϕ, |
|
или так: |
r |
|
(1.3.19) |
|
E = − φ, |
||
Знак минус говорит о том, что вектор E направлен в сторону уменьшения потенциала электрического поля.
32

1.3.5.Безвихревой характер электростатического поля
Из условия E = − φ следует одно важное соотношение, а именно:
величина векторного произведения [ ,E] для стационарных электрических полей всегда равна нулю. Действительно, по определению,
имеем
|
|
ri rj kr |
|
ri rj kr |
|
|
|
|||||||||
r |
|
∂ ∂ ∂ |
|
∂ |
|
∂ ∂ |
|
|
, |
|||||||
[ ,E] = |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
ϕ = 0 |
|
|
∂x ∂y ∂z |
∂x ∂y ∂z |
||||||||||||||
|
|
|
|
|
|
|||||||||||
|
∂ϕ∂ϕ∂ϕ |
|
∂ |
|
∂ ∂ |
|
|
|
||||||||
|
|
∂x ∂y ∂z |
|
|
|
|
|
|||||||||
|
|
|
∂x |
|
∂y |
|
∂z |
|
|
|
||||||
поскольку определитель содержит две одинаковые строки.
Величина [ ,E] |
называется ротором, или вихрем, и обозначается |
|
r |
|
|
как rot E. |
|
|
Мы получаем важнейшее уравнение электростатики |
|
|
|
rot E = 0 . |
(1.3.20) |
Таким образом, кулоновское электростатическоеполе – безвихревое.
Согласно теореме Стокса между контурным и поверхностным ин-
тегралами существует следующая связь: r
∫(E,dl) = ∫rot EdS = 0,
L S
где контур L ограничивает поверхность S, ориентация которой определяется направлением вектора положительной нормали n :
dS = nrdS .
Поэтому работа при перемещении заряда по любому замкнутому пути в электростатическом поле равна нулю.
1.3.6.Силовые линии и эквипотенциальные поверхности
Направление силовой линии (линии напряженности) в каждой точке
совпадает с направлением E . Отсюда следует, что напряженность E
равна разности потенциалов U на единицу длины силовой линии.
Именно вдоль силовой линии происходит максимальное изменение
потенциала. Поэтому всегда можно определить E между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическомr поле силовые линии – прямые. Поэтому здесь
определить E наиболее просто:
33

E = U . |
(1.3.21) |
l |
|
Теперь дадим определение эквипотенциальной поверхности. Вооб-
ражаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности –
φ = φ(x, y, z) = const. |
(1.3.22) |
Графическое изображение силовых линий и эквипотенциальных поверхностей показано на рис. 1.3.3.
Рис. 1.3.3
Вектор напряженности E в каждой точке направлен по нормали к эквипотенциальной поверхности.
Эквипотенциальных поверхностей можно провести сколько угодно много. По rгустоте эквипотенциальных поверхностей можно судить
о величине E ; это будет при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине. r
Формула E = −gradφ выражает связь потенциала с напряженно-
стью и позволяет по известным значениям φ найти напряженность поля в каждой точкеr . Можно решить и обратную задачу, т.е. по известным
значениям E в каждой точке поля найти разность потенциалов между двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть вычислена как
2 r r
A12 = q∫(E,dl).
1
С другой стороны, работу можно представить в виде
2 |
r |
r |
A12 = q(ϕ1 −ϕ2 ), тогда ϕ1 −ϕ2 = ∫ |
(E,dl). |
|
1 |
|
|
34
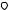
Интеграл можно брать по любой линии, соединяющей точку 1 и точку 2, ибо работа сил поля не зависит от пути. Для обхода по замкнутому контуру ϕ1 = ϕ2 получим
∫(E,dl) = 0,
т.е. пришли к известной нам теореме о циркуляции вектора напряженности. Из обращения в нуль циркуляции вектора E следует, что линии
E электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах (истоки) и на отрицательных зарядах заканчиваются (стоки) или уходят в бесконечность (рис. 1.3.3).
Это соотношение верно только для электростатического поля. Впоследствии мы с вами выясним, что поле движущихся зарядов не является потенциальным и для него это соотношение не выполняется.
1.3.7. Расчет потенциалов простейших электростатических полей
Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами.
Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостями
Связь напряженности с потенциалом E = − |
dφ |
, тогда |
|
dl |
|||
|
|
||
dφ = −Edl , |
(1.3.23) |
||
где E = σ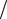 ε0 – напряженность электростатического поля между заря-
ε0 – напряженность электростатического поля между заря-
женными плоскостями, найденная в п. 1.2.5 с помощью теоремы Остроградского – Гаусса; σ = q/S – поверхностная плотность заряда.
Теперь, чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение (1.3.23):
|
|
|
|
|
|
2 |
|
|
σ x2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
∫dϕ = − |
|
|
|
∫dx; |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
ε0 x |
|
|
|
|
|
|
|||
|
|
|
σ |
|
|
|
|
|
|
|
|
1 |
|
σ |
|
|
|
|
ϕ − ϕ |
|
= − |
(x |
|
− x |
), или ϕ |
|
−ϕ = |
(x |
|
− x ). |
(1.3.24) |
||||||
|
|
|
|
|
|
|||||||||||||
1 |
2 |
|
ε0 |
2 |
|
1 |
|
|
|
|
2 |
1 |
ε0 |
2 |
1 |
|
||
При x1 = 0 |
и x2 = d |
ϕ |
|
−ϕ = |
σd . |
|
|
|
|
(1.3.25) |
||||||||
|
|
|
|
|
|
|
2 |
1 |
|
ε0 |
|
|
|
|
|
|
||
На рис. 1.3.4 изображена графическая зависимость напряженности E и потенциала φ от расстояния между плоскостями.
35

Рис. 1.3.4
Разностьпотенциаловмеждуточкамиполя, образованногозаряженной бесконечнодлиннойцилиндрическойповерхностью
В п. 1.2.5 с помощью теоремы Остроградского – Гаусса была вычислена напряженность поля для бесконечного цилиндра. Воспользовавшись полученным результатом, найдем разность потенциалов для этой поверхности.
|
|
|
2 |
|
λ |
r2dr |
|
|
|||
Так как dφ = −Edr, то ∫dϕ=− |
|
∫ |
r |
, отсюда найдем разность |
|||||||
2πε |
|||||||||||
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
0 r |
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
потенциалов в произвольных точках 1 и 2: |
|
|
|
||||||||
ϕ |
2 |
−ϕ = − |
λ |
ln r2 = − |
q |
ln r2 . |
|||||
|
|
||||||||||
|
1 |
|
2πε0 |
|
r1 |
|
2πε0l r1 |
||||
|
|
|
|
|
|
||||||
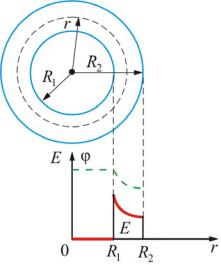
На рис. 1.3.5 изображена зависимость напряженности E и потенциала φ от r. (Здесь и далее E изображена сплошной линией, а φ –
пунктирной.)
|
λ |
|
ln |
1 |
= const внутрина |
|
|
|
|
||
2πε |
|
|
R |
||
|
0 |
|
|||
|
|
|
|
|
|
φ = поверхностицилиндра; |
|||||
|
λ |
|
|
r |
|
|
|
|
|
|
|
2πε |
|
ln |
R − внецилиндра |
||
|
|
||||
|
|
0 |
|
|
|
Рис. 1.3.5
36
Разность потенциалов между обкладками цилиндрического конденсатора
Проведя выкладки, как и в предыдущем случае, получим разность потенциалов, которая будет равна
ϕ |
2 |
− ϕ = − |
λ |
ln r2 . |
(1.3.27) |
|
|||||
|
1 |
2πε0 |
r1 |
|
|
|
|
|
|
Таким образом, внутри меньшего цилиндра имеем φ = const , Е = 0;
между обкладками потенциал уменьшается по логарифмическому закону, а вторая обкладка (вне цилиндров) экранирует электрическое поле, и φ и Е равны нулю:
На рис. 1.3.6 изображена зависимость напряженности E и потенциала φ от r.
|
λ |
|
ln |
R2 |
= const −внутрименьшего |
|||
|
|
|
|
|
||||
2πε |
|
R |
||||||
|
|
0 |
|
1 |
|
|
|
|
цилиндра (r < R1 ); |
||||||||
|
λ |
|
|
r |
|
|
||
|
|
|
|
|
||||
φ = |
|
|
ln |
|
|
−междуцилиндрами |
||
2πε0 |
R1 |
|||||||
|
|
|
|
|||||
(R < r < R |
); |
|||||||
|
1 |
|
|
|
|
2 |
|
|
0 − вне цилиндров.
Рис. 1.3.6
Разность потенциалов между точками поля, образованного заряженной сферической поверхностью
Напряженность поля сферы (рис. 1.3.7) определяется формулой
|
|
|
|
|
E(r) = |
|
|
|
q |
|
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
4πε0r2 |
|
|
|
|
|
|
|
||||||||
Так как dφ = −Edr , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
r2 |
q dr |
|
q |
|
1 |
|
r |
|
q |
|
1 |
|
1 |
|
q |
|
|||||
|
|
|
|
|
|
||||||||||||||||
φ1 − φ2 = ∫ |
|
|
|
2 |
|
|
|
|
|
||||||||||||
|
|
|
= |
|
|
− |
|
|
r1 |
= |
|
|
|
|
− |
|
, т.е. φ = |
|
. |
||
4πε0 r |
2 |
|
|
|
|
|
|
4πε0r |
|||||||||||||
r1 |
|
|
4πε0 |
|
r |
|
|
4πε0 r1 |
|
r2 |
|
||||||||||
37
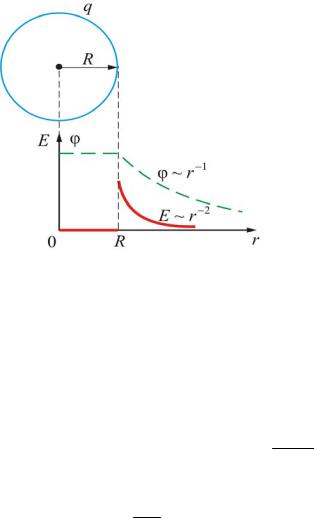
|
q |
|
|
|
σR |
|
|
|
|
|
|
|
= ε |
|
= const − внутрии |
4πε |
|
R |
|
||||
|
|
0 |
|
|
|
0 |
|
φ = на поверхностисферы (r ≤ R); |
|||||||
|
q |
|
|
|
|
|
|
|
|
|
|
|
− внесферы(r > R). |
||
4πε |
|
r |
|||||
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
Рис. 1.3.7
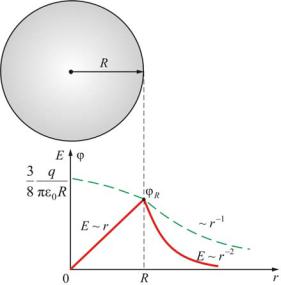
Разность потенциалов внутри равномерно заряженного шара
Имеем диэлектрический шар (рис. 1.3.8), заряженный с объемной плотностью
ρ = 4π3qR3 .
Напряженность электрического поля внутри равномерно заряжен-
ного шара E(r) = ρr . 3ε0
Теперь найдем разность потенциалов внутри шара:
|
|
2 |
|
|
ρ |
2 |
|
|
|
ρ |
(r2 −r2 ), |
||
ϕ |
2 |
−ϕ = −∫ Edr = − |
|
|
∫rdr = − |
|
|||||||
|
|
|
|
|
|||||||||
|
1 |
|
|
3ε0 1 |
|
|
|
6ε0 2 1 |
|||||
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
или |
|
|
|
|
|
|||
|
|
|
|
|
|
q(r2 |
−r2) |
|
|
|
|||
|
|
ϕ −ϕ |
2 |
= |
|
2 |
1 |
|
. |
|
|||
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
4πε02R3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Отсюда находим потенциал шара.
38
|
3q |
|
|
−вцентрешара (r = 0); |
|||||
|
|
|
|
|
|||||
8πε |
|
R |
|||||||
|
|
0 |
|
|
|
|
|
|
|
|
q |
|
|
|
|
r 2 |
|
||
|
|
|
|
|
3− |
|
|
− |
|
|
|
|
|
R |
2 |
||||
8πε0 R |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
φ = внутришара(r ≤ R); |
|||||||||
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4πε0 r −на поверхностии |
|||||||||
|
|||||||||
внешара(r ≥ R).
Рис. 1.3.8
Из полученных соотношений можно сделать следующие выводы:
•С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.
•Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
•Потенциал поля – всегда непрерывная функция координат.
Контрольные вопросы. Упражнения
1.Какова связь между напряженностью и потенциалом электростатического поля? Выведите ее и объясните. Каков физический смысл этих понятий?
2.Чему равна работа по перемещению заряда вдоль эквипотенциальной поверхности?
3.Дайте определения потенциала данной точки электростатического поля и разности потенциалов двух точек поля. Каковы их единицы?
4.С помощью теоремы Остроградского – Гаусса рассчитайте и изобразите графически:
•разность потенциалов между точками поля, образованного заряженной бесконечнодлиннойцилиндрическойповерхностью;
•разность потенциалов между обкладками конденсатора;
•разность потенциалов между точками поля, образованного заряженной сферической поверхностью;
•разность потенциалов внутри равномерно заряженного шара.
5. По поверхности сферы радиусом 30 см распределен заряд 4 нКл. Чему равен потенциал в центре сферы?
39
1.4. Диэлектрики в электростатическом поле
1.4.1. Поляризация диэлектриков
Все известные в природе вещества, в соответствии с их способностью проводить электрический ток, делятся на три основных класса:
диэлектрики, полупроводники и проводники. Если удельное сопротив-
ление у проводников равно ρпр =10−8 −10−6 Ом·м, то у диэлектриков
ρд =108 −1018 Ом·м, а полупроводники занимают промежуточную об-
ласть – ρд > ρп/п > ρпр.
В идеальном диэлектрике свободных зарядов, т.е. способных пере-
мещаться на значительные расстояния (превосходящие расстояния между атомами), нет. Но это не значит, что диэлектрик, помещенный в электростатическое поле, не реагирует на него, что в нем ничего не происходит.
Любое вещество состоит из атомов, образованных положительными ядрами и отрицательными электронами. Поэтому в диэлектриках происходит поляризация.
Смещение электрических зарядов вещества под действием электрического поля называется поляризацией. Способность к поляризации является основным свойством диэлектриков.
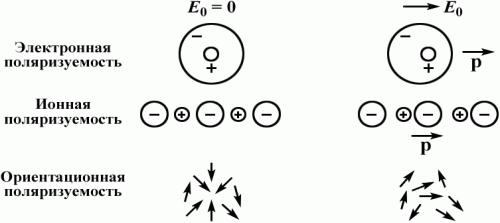
Поляризация диэлектрика включает составляющие – электронную, ионную и ориентационную (дипольную). На рис. 1.4.1 проиллюстрированы механизмы этих видов поляризации.
Рис. 1.4.1
Электронная поляризуемость обусловлена смещением электронной оболочки атома относительно ядра. Ионная поляризуемость вызвана смещением заряженных ионов по отношению к другим ионам. Ориен-
40
