Воскобойников Задорожный Основы MathCAD

a x2 + b x + c 0 solve,x →

Приведем пример решения тригонометрического уравнения.

Пример 8.1.2

2. Второй метод состоит в использовании меню Символы (Symbols)на панели инструментов.

Для этого:

•Введите выражение левой части уравнения.

•Выделите переменную. Если переменная встречается в выражении несколько раз, выделите её в любом месте выражения (переменная должна быть охвачена уголком голубого цвета).

•Выберите из главного меню: Символы Переменная Вычис-

лить (Symbols Variable Solve).

Пример 8.1.3:

Задание:

А. Решите уравнения относительно θ: cos(θ) + 2·sin(θ)

sin(θ) + sin(2·θ)

Б. Решите уравнения относительно x: x2 - 5·x + z

5x3 - 24x2 -1 e-x – ax2

8.2. Решение уравнения с одним неизвестным (функция root)

Для численного решения простейших алгебраических уравне-

ний вида F(x)=0 можно использовать функцию root. Функция root

имеет две формы вызова: root(f(x),x) и root(f(x),x,a,b).

root(f(x),x) - здесь функция root возвращает с заданной точностью значение переменной x, при котором выражение или функция f(x) обращается в 0. Перед вызовом функции необходимо задать начальное значение переменной x. Если уравнение имеет несколько корней, то последующие вычисляются следующим образом: для нахождения второго корня первый исключается делением функции F(x) на (x-x1); для нахождения третьего корня делением функции F(x) на (x-x1)(x-x2) исключаются первый и второй корни и т.д. Функция реализует вычисление итерационным методом, до тех пор, пока два последовательных вычисленных значений x, удовлетворяющих условию решения не будут отличаться на величину погрешности. Погрешность задаётся системной переменной TOL. По умолчанию TOL=0x10-3. Как и любую переменную TOL можно переопределить.

Перед решением уравнения желательно построить график функции f(x). По графику будет видно, имеет ли функция действительные корни (пересечение с осью). Если есть, то надо выбирать начальное значение ближе к корню. Если корней несколько, то, за-

84

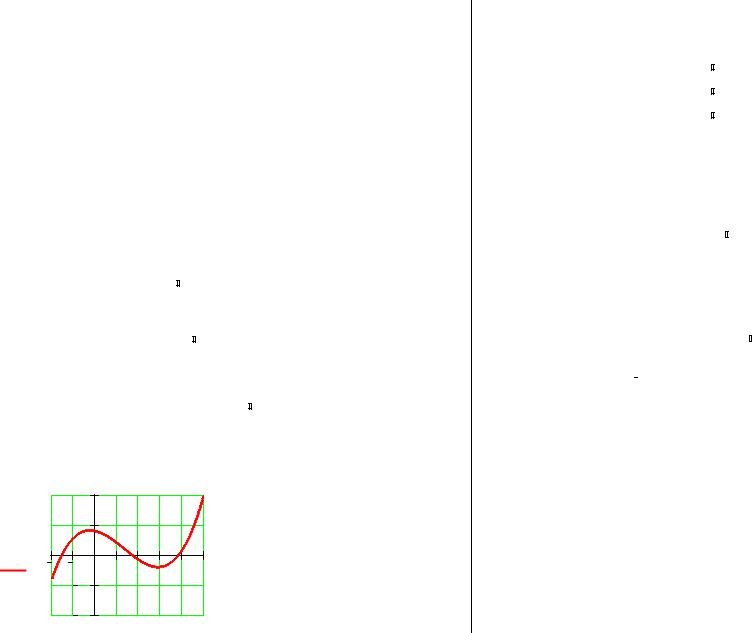
давая свое начальное приближение, можно вычислить каждое из них.

root(f(x),x,a,b) – здесь a и b это границы численного интервала для поиска корней. При этом нет необходимости задавать начальное значение x, поскольку переменная определена в заданном интервале [a,b].

Рассмотрим пример решения уравнения : 2x3 – 8x2 - 4x +20 = 0.

•Запишем коэффициенты уравнения в виде:

a3 := 2 a2 := −8 a1 := −4 a0 := 20

•Определим функцию:

f(x) := a3 x3 + a2 x2 + a1 x + a0

•Зададим начальное приближение:

x:= 0

•Найдем первый корень:

•Найдем второй корень:

•Найдем третий корень:

Построим график функции f(x) (рис 8.1):

25

50

Рис. 8.2.1. График функции f(x)

По графику видно, что корни уравнения лежат в интервалах: [-2; -1], [1.5; 2] и [3.5; 4]. Найдем их с помощью второго вида вызова функ-

ции root(f(x),x,a,b).

Поиск экстремальных значений

С помощью функции root можно определить экстремумы функции. Для этого находим значения x, при котором производная функции равна нулю. По графику видно, что первый экстремум лежит в интервале [-1; 0]

и его значение равно: f(xe1) =

а второй – в интервале [2.5; 3.5]

f(xe2) =

Задание: Решить уравнения графически и численно; найти экстре-

мумы:

А. x2 – 2 + 0.5x = 0; Б. 2x4 – x2 – 10 = 0; В. x3 – 10x + 2 =0.

8. 3. Вычисление корней полиномов (функция polyroots)

Для вычисления всех корней алгебраического уравнения порядка n,

имеющего вид

anxn + … + a2x2 + a1x + a0

рекомендуется использовать функцию polyroots. При вызове функции polyroots надо определить вектор коэффициентов полинома (начиная со свободного члена) и затем использовать его как ар-

гумент это функции - polyroots(ν). Здесь ν – вектор коэффициентов

алгебраического уравнения. Пример: Решим уравнение x3 – 3x -1 = 0

Вектор создается с помощью панели Матрицы . В примере для матрицы устанавливаются параметры: 1 столбец и 4 строки.

Другой способ вычисления корней полинома с помощью функции polyroots заключается в следующем:

•Определить полином как функцию;

•Использовать в панели Символы ключ ‘coeffs’, формирующий вектор коэффициентов.

Пример 8.3.1.

f(x) := 3x3 − 4x + 5

Задание 8.3.1. Решите уравнения:

1.x3 + (3 + 2i)x2 + (-4 + 6i)x – 8i = 0;

2.2x4 – x2 – 10 = 0;

3.3x4 + 4x3 – 12x2 – 5 = 0.

8.4. Решение систем линейных уравнений

Система линейных алгебраических уравнений (СЛАУ) представляется в виде:

a1,1x1 + a1,2x2 + … + a1,mxm = b1 a2,1x1 + a2,2x2 + … + a2,mxm = b2

. . .

an,1x1 + an,2x2 + … + an,mxm = bn

n уравнений относительно m неизвестных. В матричном виде систему можно записать как

Ax = b,

где A – матрица размерности n x m, b – вектор правой части. Условием наличия решения являются: а) матрица A является квадратной, т.е. n=m; б) матрица A является невырожденной, т.е. ее определитель не равен нулю.

Для вычисления СЛАУ следует использовать функцию lsolve, обращение к которой имеет вид: lsolve(A,b), где A – матрица системы, b – вектор правой части. Решение СЛАУ – вектор с т проекциями.

Пример 8.4.1. Дана система уравнений

2x1+12x2 4 = 40x2 + 7x3 = 410x1+5x2 =- 20

Используя функцию lsolve, найти решение этой системы и выполнить проверку найденного решения.

Определим матрицу коэффициентов:

Задание 8.4.1. Решите системы уравнений:

100x1+ 6x2 2x3 = 200 А. 6x1+ 200x2 10x3 =600

x1 2x2 100x3 =500

10x1 + x2 + x3 =12 Б. 2x1+10x2 + x3 =132x1+ 2x2 +10x3 =14

8.5. Решение систем нелинейных уравнений

Для решения систем уравнений надо использовать специальный вычислительный блок Given, имеющий следующую структуру:

<Начальные условия> Given

<Уравнение> <Ограничения>

<Вызов функции Find или Minerr>

Ключевое слово Given показывает Mathcad, что далее следует система уравнений. Между левой и правой частями уравнений или неравенств должны стоять знаки =, >, <, ≤, ≥, которые вводятся из панели Булево.

Функция Find(z1, z2, … ) – возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных. Пример 8.5.1. Решить систему нелинейных алгебраических уравнений:

89

y −3 x −8 = 0

y − x2 = 0

Определим начальные приближения для решения этой системы. Построим графики (рис. 8.5.1) указанных функций, чтобы фиксировать точки их пересечений:

y1(x)

y2(x)

x

Рис 8.5.1. График функций Найдем первый корень.

•Зададим начальные приближения для нахождения первого корня:

x := −2 y := 2

•Введем ключевое слово:

Given

•Введем уравнения:

y − 3 x − 8 0 y − x2 0

•Проекция первого решения

F := Find(x,y) F =

Найдем второй корень:

Пример 8.5.3. В качестве тестового функционала при поиске точки минимума часто используется функционал Розенброка:

f (x, y) =100 (y − x 2 ) + (1 − x)2 .

«Поверхность» этого функционала напоминает глубокий овраг, что сильно осложняет работу многих алгоритмов минимизации. Требуется вычислить точку минимума функционала при ограничениях:

x ≥ 0; y ≥ 0; y ≤ 9 − x .

Документ MathCAD решения этой задачи показан на рис. 8.5.1.

f ( x , y) = 3.538 × 10− 8

Рис. 8.5.2. Минимизация функции Розенброка

Задание 8.5.1. Используя блок Given, решить следующие системы уравнений:

Проверить найденные решения.

ТЕМА 9. РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ

В практике выбора решения наиболее часто мы обращаемся к задачам оптимизации. Например, в ряде задач проектирования существует необходимость определить значения параметров, которые доставляют максимум или минимум некоторому функционалу (или целевой функции), зависящему от этих параметров. Если на значения этих параметров не накладываются какие-либо ограничения (например, требование положительности), то приходим к задаче безус-

ловной оптимизации (или оптимизации без ограничений). Если за-

даны ограничения, определяющие допустимые значения парамет-

ров, то приходим к задаче условной оптимизации (оптимизации с ограничениями). Вторая задача отличается от первой тем, что решение ищется только среди допустимых значений или, иначе, на до-

пустимом множестве параметров.

9.1. Решение оптимизационных задач без ограничений

Для этого используются две функции MathCAD:

•Maximize(f,<список параметров>) – вычисление точки максимума;

•Minimize(f,<список параметров>) – вычисление точки мини-

мума,

где f – имя минимизируемого функционала, определенного до обращения к функции; <список параметров> – содержит перечисление (через запятую) имен параметров, относительно которых решается оптимизационная задача.

Функции Maximize и Minimize возвращают вектор неизвестных, при которых исследуемая функция имеет максимальное или минимальное значение соответственно.

Перед обращением к функциям Maximize, Minimize надо обязательно задать начальное значение параметров оптимизации.

Пример 9.1.2. Дан функционал:

Определить значения u, v, при которых f(u,v) достигает максимального значения.

Документ MathCAD, решающий эту задачу приведен на рис. 9.1.1. В последних строках документа выполнена проверка найденного решения на максимум.

Определить точки минимума и максимума этих функционалов.

9.2. Решение оптимизационных задач с ограничениями

Используются те же функции Maximize, Minimize, но должны использоваться в составе блока решения Given (см. (7.2)). Перед блоком решения надо задать начальные значения искомых переменных. Внутри блока задаются ограничения в виде равенств или нера-

венств, определяющие допустимую область значений параметров оптимизации.

Пример 9.2.1. Дан функционал:

Определить значения a, b, доставляющие максимальное значение функционала (9.2.1) и удовлетворяющие неравенствам (9.2.2).

Документ MathCAD, решающий эту задачу, показан на рис. 9.2.1. Точка «старта» алгоритма берется из допустимой области, определяемой ограничениями (9.2.2).

Рис. 9.2.1. Условная максимизация функционала (9.2.1) Пример 9.2.3 (задача линейного программирования). Цех мало-

го предприятия должен изготовить 100 изделий трех типов

(x1, x2 , x3 ) и не менее 20 штук изделий каждого типа. На изделия

уходит 4, 3.4 и 2 кг металла соответственно, при его общем запасе 340 кг, а также расходуются по 4.75, 11 и 2 кг пластмассы, при ее общем запасе 700 кг. Прибыль, полученная от каждого изделия равна 4, 3 и 2 р. Определить, сколько изделий каждого типа необходимо выпустить для получения максимальной прибыли в рамках установленных запасов металла и пластмассы.

Документ MathCad, решающий эту задачу приведен на рис. 9.2.3.

Рис. 9.2.3. Решение задачи линейного программирования

Пример 9.2.4 (задача нелинейного программирования). Пусть вектор v состоит из трех проекций и дан функционал:

N (v) = v 2 + 2v1 −v2 + 2v3.

Вычислить точку минимума этого функционала при ограничениях:

3

∑vi =1, vi ≥ 0.2, i =1,3.

i=1

Документ MathCAD, решающий эту задачу, показан на рис. 9.2.4.

Рис. 9.2.4. Решение задачи нелинейного программирования

Задание 9.2.1 (задача линейного программирования). Дан функционал:

F(x) = 2x0 +9x1 +15x2 .

Определить точку максимума этого функционала при ограничениях:

x0 ≥ 0; x1 ≥ 0; x2 ≥ 0; 7x0 + 3x1 + x2 ≤ 47; 0.5x0 −3x1 +8x2 ≤ 25;

9x0 + 2x1 −10x2 ≤ 29.

Вычислить значения функционала в этой точке. Ответ: максимум функционала достигается в точке (0, 13, 8).

Задание 9.2.2 (задача линейного программирования). Из металлического листа прямоугольной формы необходимо сварить бак максимального объема. Размеры листа L=1, M=2. Необходимо про-

извести вырез по углам прямоугольника на величину a и сформировать стороны бака.

Определить величину a, при которой объем бака, будет максимальным.

Ограничения: a< L2 и a< M2 .

Рис.9.2.6. Заготовка для бака

Задание 9.2.3 (задача квадратичного программирования). Дан функционал:

Q(u, v,ω) = u(15 −u) +5v(20 −v) + 2ω(12 −ω).

Определить точку максимума этого функционала при ограничениях:

u ≥ 0; v ≥ 0; ω ≥ 0; 3u +2v +4ω ≤100;

u +7v +ω ≤ 90.

Ответ: максимум функционала достигается в точке (7.5, 10, 6).

ограничениях:

u ≥ 0; v ≥ 0; ω ≥ 0; 3u +2v +4ω ≤100;

u +7v +ω ≤ 90.

Ответ: максимум функционала достигается в точке (7.5, 10, 6).

ТЕМА 10. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Большинство сложных физических и научно-технических задач базируются на решении систем дифференциальных уравнений. В MathCAD имеется много встроенных функций для решения обыкновенных дифференциальных уравнений и систем дифференциальных уравнений.

10.1Решение одного обыкновенного дифференциального

уравнения

MathCAD позволяет без дополнительных преобразований численно решить дифференциальное уравнение, явно разрешенное относительно старшей производной (рис. 10.1).

а) б)

Рис. 10.1. Примеры уравнений, разрешенного (а) и неразрешенного (б) относительно старшей производной

Решение осуществляется с помощью специального блока Given-Odesolve, состоящего из следующих компонент:

•Ключевое слово Given.

•Дифференциальное уравнение, записанное в традиционной математической форме со следующими особенностями: а) вместо простого знака равенства «=» используется оператор логического равенства (вводится из панели Булево); б) при обозначении интегрируемой функции всегда указывается аргумент (то есть вместо функции x(t) нельзя писать просто x); в) при записи производных использу-

ются либо стандартные операторыи, либо ставятся (с помощью Ctrl-F7) символы производной, например x’(t), x’’(t).

• Указание начальных или конечных граничных условий интег-

рируемой функции и ее производных (за исключением старшей),

входящих в уравнение. Значения вводятся в традиционной форме с использованием оператора логического равенства. Число значений должно совпадать с порядком уравнения. Для уравнения второго по-

рядка вида должны быть заданы начальные значения функции и ее первой производной, например x(0) = 1; x’(0) = 0,5. Для ввода символа производной «’» используется комбинация клавиш Ctrl-F7.

4. Обращение к функции Odesolve(x,xk,n), здесь первый аргумент x- всегда имя независимой переменной; второй аргумент xk - конечное значение независимой переменной; третий (необязательный) аргумент n - количество шагов интегрирования, за которые должно быть найдено решение. Odesolve возвращает решение в виде функции (а не в виде массива), представляющей приближенное (численное) решение дифференциального уравнения на заданном интервале времени. Данная функция может быть использована для определения значений интегрируемой функции в различных точках, а также для построения графика.

Пример 10.1. Решим дифференциальное уравнение

4 x''(t) + x(t) t при граничных условиях x(C)=A и x(D)=B; найдем значения x и построим график решения.

A := 4 B := 10 C := −3 D := 6

Given

x( t)

d x( t) dt

t

10.2.Численное решение систем обыкновенных дифференциальных уравнений

Дифференциальные уравнения, входящие в систему, должны иметь первый порядок (то есть содержать только первые производные). Все уравнения должны быть предварительно разрешены относительно производных и записаны в нормальной форме вида

.

Для преобразования уравнений в нормальную форму есть два основ-

ных подхода:

1.Понижение порядка уравнений путем замены переменных.

2.Приведение системы дифференциальных уравнений к явному виду путем ее решения относительно производных.

Для решения систем дифференциальных уравнений используются функции Odesolve и rkfixed.

Обращение к функции Odesolve выглядит так:

Odesolve((вектор имен неизвестных),x,xk,n).

Обращение к rkfixed выглядит так: rkfixed(y ,x1, x2 ,npoints, D), где

y=вектор начальных условий размерности n;

x1, y2 = граничные точки интервала, на которых ищется решение; npoints = число точек, в которых ищется решение;

D(x,y) = функция, возвращающая значение в виде вектора из n элементов, содержащие первые производные неизвестных фукций.

Пример 10.2. Решим систему дифференциальных уравнений с помощью функции Odeselve:

2 x'(t) + x(t) − y(t) + z(t) 0 , z' (t) − z(t) x(t) + y(t) ,

4 y'(t) + y(t) x(t) + z(t) , с граничными условиями.

Приведем документ Mathcad с решением системы ДУ

Given

d z(t) − z(t) x(t) + y(t) dt

Условия:

x(0) 0 y'(0) −1 z'(0) −1

Пример 10.3. Решим систему дифференциальных уравнений с помощью функции rkfixed:

u’’ = 2v , v’’ =4v – 2u

с начальными условиями: u’(0) = 1.5, u(0) = 1.5, v(0) = 1, v’(0) = 1.

Приведем документ Mathcad с решением системы ДУ