Воскобойников Задорожный Основы MathCAD

Mathcad включает два набора функций для чтения и записи данных:

• READ, WRITE и APPEND - читаютилизаписывают одно числовое значение за раз. Эти функции используются с неструктурированными данными.

•READPRN, WRITEPRN и APPENDPRN - считывают целую матрицу из файла со строками и столбцами данных или записывают в виде такого файла матрицу из Mathcad, т.е. выполняют действия со структурированными данными.

Если два равенства в рабочем документе используют WRITE или WRITEPRN с одним аргументом, данные из второго равенства запишутся поверх данных из первого. Используйте APPEND или АРPENDPRN, если нужно сохранить первую порцию данных. Эти функции дописывают новые данные к существующему файлу. ЕслифункцииAPPENDPRN, READPRN иWRITEPRN добавляют, считываютизаписываютвфайлпрямоугольнуюматрицу (число— частныйслучайматрицыразмерностью 1x1), тофункцииAPPEND, READ иWRITE добавляют, считываютизаписываютодночисло,

Функции Read, Writer Append могут использоваться с дискретными аргументами, остальные — нет.

Итак, формат функций доступа к файлам:

•v:=READ("file") - cчитывает значение из файла данных. Возвращает скаляр.

•WRITE("file"):= vi - записывает значение в файл данных. Если файл уже существует, заменяет его на новый файл.

•APPEND("file"):= vi - дописывает значение к существующему файлу.

•А : = READPRN("file") - читает структурированный файл данных. Возвращает матрицу. Каждая строка в файле данных становится строкой в матрице. Число элементов в каждой строке должно быть одинаковым.

•WRITEPRN("file") := A - записывает матрицу в файл данных. Каждая строка матрицы становится строкой в файле.

•APPENDPRN("file"):= А - дописывает матрицу к существующему файлу. Каждая строка в матрице становится новой строкой в файле данных. Существующий файл должен иметь столько же столбцов, как и матрица А.

Замечание. Создаваемый в MathCAD файл данных достаточно просто просмотреть и отредактировать в текстовом редакторе, отображающем ASCII-данные. Примерами таких редакторов может служить программа Блокнот, входящая в состав Windows (Программы Стандартные), а также редакторы языков программирования – PASCAL, СИ и др.

Здесь предполагается, что :

А - обозначает массив (вектор или матрицу); vi - обозначают отдельные элементы вектора v;

file- - любое допустимое имя переменной Mathcad; i - дискретный аргумент.

ВНИМАНИЕ: Привводевназваниефункцииименифайланезабывайтеставитькавычки. Еслинеуказыватьрасширение, поумолчанию подразумевается расширение.prn

Пример5.1.

•С помощью палитры матрица построим матрицу А и транспонируемеёвматрицу АТ .

• Создадим на диске “С: “ в директории “temp” файл с именем primer.prn, содержащийзначениематрицыАТ.

WRITEPRN("C:\temp\primer") := АT

• Проверим результат. С помощью проводника Windows откроем диск “ С: ” и перейдем в директорию “temp”. Найдем созданный файл primer.prn и с помощью программы “блокнот ” прочитаем его. Закройте файл, чтобыобеспечитькнему доступиздругихпрограмм.

•Аналогично построим матрицу В и транспонируем её в матрицу ВТ

идобавим транспонированнуюматрицу ВТ ксозданному файлу:

APPENDPRN("C:\temp\primer.prn") := ВT.

• Проверимполученныйрезультатспрограммы “Блокнот”. Считаем данныеизэтогофайлавматрицу К:

К:= READPRN("C:\temp\primer.prn")

Прочитаем содержимоематрицыК. Дляэтогонаберем: “К=” Наэкранеполучимзначение

K =

Пример 5.2. Записать в файл матрицу В, k-й столбец которой есть выборка из нормального распределения с математическим ожиданием μ0 =10 и среднеквадратическим отклонением σ0 = 2

(дисперсия соответственно σ02 = 4 ).

Фрагмент документа, осуществляющий запись структурированного файла, приведен на рис. 5.1. В окне программы Блокнот хорошо видна структура сформированного файла (число строк n = 5, число столбцов m = 4).

B k := rnorm(n,μ0,σ0)

WRITEPRN ( file_2 ) := B

Рис. 5.1. Запись структурированного файла

Задание 5.1. Составить фрагмент документа MathCAD, формирующий файл, содержащий два столбца:

рый формировал файл, содержащий кроме матрицы В, определяемой условиями примера 5.1, добавленную в конец файла матрицу С размерности 8×m , k-й столбец которой есть выборка из нормально-

го распределения с математическим ожиданием μ0 =10 и дисперси-

ей σk2 = 0.01 + k, k = 0, m −1.

ТЕМА 6. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

При выполнении обработки экспериментальных данных обычно возникает задача аппроксимации результатов эксперимента или приближенного вычисления значений функции в промежутках между узловымиточками(интерполяция) изаихпределами(экстраполяция). Интерполяция заключается в нахождении того или иного аппарата, позволяющего вычислять значения у(х) и промежутках между точками.

Другим понятием является аппроксимация. Обычно это подмена исходной зависимости какой-либо достаточно простой функцией или легко вычисляемой функцией. Система Mathcad предоставляет возможность аппроксимации двумя важными типами функций: ку- сочно-линейной и сплайновой.

6.1. Одномернаялинейнаяинтерполяцияиэкстраполяция

При кусочно-линейной интерполяции вычисления дополнительных точек выполняются по линейной зависимости. Графически это означает просто соединение многих точек отрезками прямых. Это выполняется с помощью функции linterp (vx, vy, x). Она соединяет точки данных отрезками прямых, создавая таким образом ломаную. Для заданных векторов абсцисс vx и ординат vy узловых точек и заданного аргумента х функция linterp возвращает значение функции при ее кусочно-линейной аппроксимации (интерполяции). Аргументы vx и vy должны быть векторами одинаковой длины.

Вектор vx должен содержать вещественные значения, расположенные в порядке возрастания.

Рассмотрим пример получения линейной интерполяции.

5 4.5

4.5 4.5

1.Установим значения вектора vx в возрастающем порядке с помощью функции сортировки по 0-му столбцу:

data1׃=csort(data,0) fit(1) = 1.144

2. Выведем значения отсортированной матрицы data1:

fit(7) = 4.5

3.Введем переменные vx и vy, где vx - это вектор значений x,

аvy – вектор значений y:

vx := data1 0 vy := data1 1

4.Получим функцию fit(x), интерполирующую значенияе данных:

fit(x) := linterp(vx,vy,x)

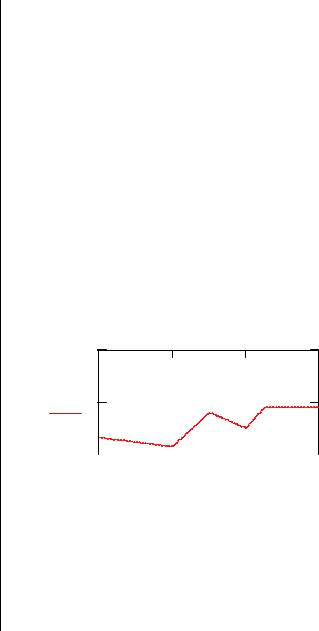
5. Построим график функции fit(x):

10

fit ( x) 5

Рис.6.1

6.Отдельные значения fit(x) внутри отрезка можем получить подставляя соответствующие значения x:

6.2.Одномерная сплайновая интерполяция и экстраполяция

Линейная интерполяция при небольшом числе узловых точек (менее 10) оказывается довольно грубой. Для экстраполяции функция linterp не применима, так как при экстраполяции используются отрезки прямых, проведенных черездвекрайниеточкиипоэтому за пределами диапазона узловых точек может вести себя непредсказуемо.

Болееточныйрезультатдает сплайноваяинтерполяция. Сплайнинтерполяция позволяет провести кривую через набор точек таким образом, что первые и вторые производные кривой непрерывны в каждой точке. Эта кривая образуется путем создания ряда кубических полиномов, проходящих через наборы из трёх смежных точек. Кубические полиномы затем состыковываются друг с другом, чтобы образовать одну кривую. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закрепленную в узловых точках.

Для осуществления сплайновой интерполяции и экстраполяции Mathcad предлагает четыре встроенные функции cspline, pspline, lspline и interp. Первые три из них служат для получения вторых производных сплайн-функций при различных видах продолжения (экстраполяции) и отличаются только граничными условиями:

•lspline(vx, vy) - возвращает вектор vs вторых производных и генерирует кривую сплайна, которая приближается к прямой линии в граничных точках;

•pspline(vx, vy) - возвращает вектор vs вторых производных и генерирует кривую сплайна, которая приближается к параболе в граничных точках;

•cspline(vx, vy) - возвращает вектор vs вторых производных и генерирует кривую сплайна, которая может быть кубическим полиномом в граничных точках.

Четвертая функция interp(vs, vx, vy, x) возвращает интерполируемое значение y(х) для заданных векторов vs, vx, vy и заданного значения х.

Таким образом, сплайн-интерполяция проводится в два этапа. На первом с помощью функции cspline, pspline или lspline отыскивается вектор vs вторых производных функции у(х), заданной векторами vx и vy ее значений (абсцисс и ординат). Затем на втором этапе для каждой искомой точки вычисляется значение у(х) с помощью функции interp.

Пример сплайновой интерполяции. Используем данные представленные в примере с линейной интерполяцией. Приведем сплайновую интерполяцию тремя видами— кубическим, линейным и параболическим.

1. С помощью функций cspline (кубический), lspline (линейный) и pspline (параболический) вычислим, соответственно, векторы vsc, vsl и vsp, которые содержат вторые производные интерполяционной кривой в рассматриваемых точках.

vsc := cspline(vx ,vy) vsl := lspline(vx ,vy) vsp := pspline(vx ,vy)

2. Найдем с помощью функции interp интерполирующие значения y(x) для каждой искомой точки по всем трем вариантам интерполяции:

fitsc (x) := interp(vsc ,vx ,vy ,x) fitsl(x) := interp(vsl ,vx ,vy ,x) fitsp(x) := interp(vsp ,vx ,vy ,x)

3. Для сравнения определим значения функции y при значении x=1 и x=7 для разных сплайн-фукций:

4. Построим графики сплайн-интерполяции

fitsc(xj) fitsl(xj) fitsp(xj)

xj

Рис.6.2. Графики интерполяции

Полученные кривыесоответствуютсплайнамскубическим, линейнымиквадратическим продолжением.

Нетрудно заметить, что при линейной интерполяции (рис.6.1) график оказывается слишком грубым — отчетливо видны точки перегибов, совпадающие с узловыми точками. В то же время сплайновая интерполяция (рис. 6.2), несмотря на малое число точек, в этом примере (их всего 6), дает прекрасные результаты: график функции оказывается плавным и точки его перегиба вообще незаметны.

Задание 6.1. Выполните сплайновую интерполяции скубическим, линейнымиквадратическим продолжением для данных:

x=(0.4 1.6 3.1 4 4.2 5) y=(25 11 9.4 16.2 21.2 26).

6.3Регрессия

Вотличие от функций интерполяции, рассмотренных выше, функции регрессии не требуют, чтобы аппроксимирующая кривая или поверхность проходила через точки данных. Функции регрессии гораздо менее чувствительны к ошибкам данных, чем функции интерполяции. Метод регрессии заключается в сле-

дующем. Пусть значения функции yi заданы на множестве значений аргумента xi (i=0…N).Требуется найти аппроксимацию

(приближение) F(x, K0, K1, … , Km) = K0F0(x) + K1F(x)+…+KmFm(x) такое, чтобы функция F(x) проходила как можно ближе к точкам (xk, yk). Если в качестве меры близости мы возьмем сумму квадратов отклонений (F(xi)-yi)2, то получим задачу среднеквадратической аппроксимации. В этом случае го-

ворят о регрессии методом наименьших квадратов. Функция регрессии является линейной комбинацией функций F0(x), F(x), … Fm(x), причем сами функции могут быть нелинейными. Нашей целью является отыскание коэффициентов Ki. Для решения этой задачи может быть использована функция linfit(x,y,F), где x

– вектор значений аргумента, y – вектор значений функции в точках xi, F – вектор функций, составляющих функциональный базис. Функция linfit возвращает вектор K коэффициентов регрессии, при которой среднеквадратичная погрешность приближения исходных точек, оказывается минимальной.

Пример 6.1. Построим аппроксимацию, используя набор функ-

•определим векторную функцию, описывающую функциональный базис:

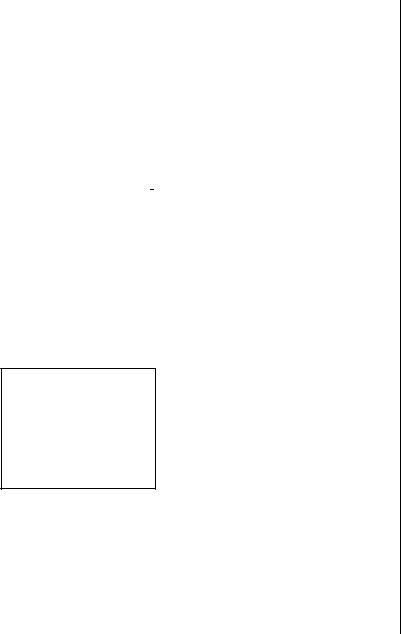
1

x

F(x) := x2

ex

•найдем коэффициенты аппроксимации Ki:

K := linfit(x,y ,F) K =

•для того, чтобы визуально оценить качество аппроксимации, построим совмещенные графики исходной и аппроксимирующей функций:

yi

g(s)

xi ,s

Задание 6.1: найдите аппроксимацию функции, заданной в точках

x:= (0.5 1 1.2 1.6 2 2.7 3.2 6),

в функциональном базисе, составленном из функций: F0=1/x; F1=1; F2=x. Постройте совмещенные графики.

Задание 6.2: найдите аппроксимацию функции y=cos(x) полиномом 4 степени на отрезке от –π /2 до π /2.

Задание 6.3: найдите аппроксимацию функции, заданной в

в функциональном базисе, составленном из функций: F0= ln(x); F1=sin(x); F2=3x. Постройте совмещенные графики.

ТЕМА 7. ВЫЧИСЛЕНИЕ РАЗВЕТВЛЯЮЩИХСЯ АЛГОРИТМОВ И ЦИКЛОВ

7.1. Вычисление разветвляющихся алгоритмов

Используемые в расчетах функции не всегда бывают непрерывными. Часто при разных значениях аргумента функция описывается разными выражениями. Отслеживание изменений функций и “склеивание ” отдельных выражений в непрерывную функцию осуществляется с помощью оператора условий – if и операций отношений. Разветвляющийся алгоритм вычисления таких функций состоит из нескольких возможных ветвей. Выбор конкретной ветви зависит от выполнения (или не выполнения) заданных условий на значения переменных алгоритма.

Оператор условий – if имеет следующий формат вызова: if (условие, выражение1, выражение2)

и используется для определения поведения функции слева и справа от точки разрыва. Точка разрыва определяется условием, задаваемым в структуре if (). Если условие выполняется, то функция принимает значение выражение1. Если не выполняется, то - выражение2. Оператор условий if вводится с клавиатуры.

Аргумент условие может быть любым, но чаще всего в условии используются операторы отношений: │ ═ │ ≥ │ ≥ │> │< │ ≠ │, выражающие отношения между сопоставляемыми числами (здесь

вертикальные черточки являются разделительным символом при перечислении). Операторы отношений вводятся из палитры Булево:

Рис. 7.1. Палитра инструментов Булево

Рассмотрим несколько примеров.

Пример 1.

Пусть имеем функцию f(x) = x2 – 1; x -2,2; x=0.1.

График f(x) имеет вид:

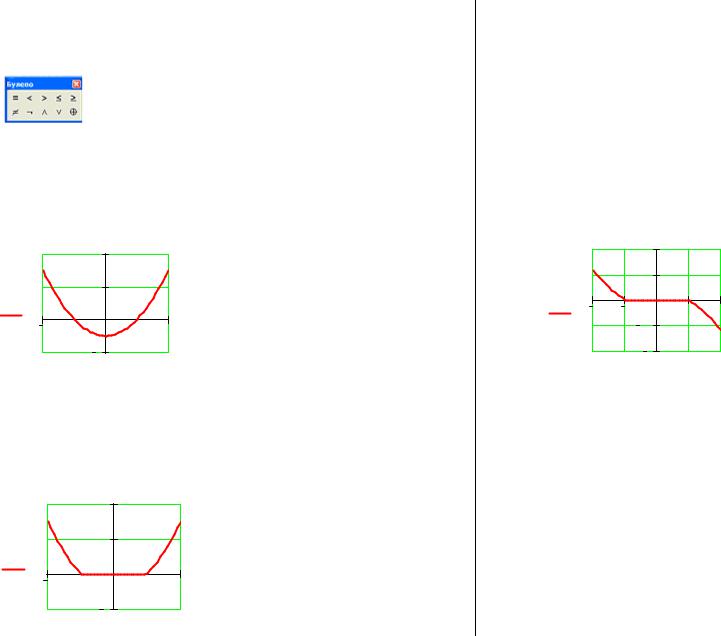
Далее, пусть функция g(x) = f (x), если f (x)>0, иначе (т.е. при отрицательных значениях f (x)) принимает значение равное 0. Запишем выражение разветвляющейся функции g(x):

g(x) := if(f(x) > 0,f(x) ,0)

График такой функции имеет вид:

Рис.7.3. График разрывной функции Если в разветвляющемся алгоритме количество ветвей больше двух,

то в качестве выражение2 будет вновь использована функция условия if.

Пример 2.

Для проверки более сложных условий используются четыре логические операции:

¬ - логическое отрицание;- исключающее ИЛИ;

- логическое ИЛИ;

- логическое И.

Пример 3. Условие определяет только положительное значение функции f(x) и определяет, что значение переменной x больше, чем - 1.8, но НЕ превышает значение 1.8. Функция и график функции показаны на рис.7.5.

g1(x) := if[(f(x) > 0) (x ≥ −1.8) ¬(x ≥ 1.8) ,f(x) ,0]

Рис.7.5. График функции с логическими условиями Задание. Используя условную функцию if, запрограммируйте

следующие разветвляющиеся алгоритмы. Постройте их графики (диапазон изменения x выберите самостоятельно).

В MathCAD имеется ряд встроенных функций, которые возвращают результат, зависящий от знака или величины аргумента, и могут использоваться при программировании разветвляющихся алгоритмов. Приведем некоторые из них:

•ceil (x) – наименьшее целое, большее или равное x;

•trunc (x) – целая часть вещественного числа x;

•floor (x) – наибольшее целое, меньшее или равное x;

•round (x, n) – округленное значение вещественного x с точностью до n знаков после десятичной точки;

•Ф(x) – функция Хевисайда – равна 0 при x < 0 и 1 в противном случае;

• sign (x) – функция знака (равна 0 если x = 0; -1, если x <0 и 1, если x >0);

ях.

7.2. Программирование циклических алгоритмов

Циклическим алгоритмом (или просто циклом) называется ал-

горитм, содержащий вычисления, повторяющиеся при различных значениях некоторой переменной, названной параметром цикла, а сами повторяющиеся вычисления составляют тело цикла.

Типы циклов. По способам организации цикла можно выделить:

а) цикл типа арифметической прогрессии; б) итерационный цикл.

Особенностью цикла типа арифметической прогрессии является изменение параметра цикла по закону арифметической прогрессии, и поэтому можно, не выполняя цикла, определить количество повторений цикла.

В итерационном цикле невозможно «априори», т.е. не выполняя вычислений, определить число повторений тела цикла из-за разнообразных условий завершения цикла.

Программирование цикла типа арифметической прогрес-

сии. Параметр такого цикла задается дискретной переменной (называемой также ранжированной переменной), и тогда конструкции, входящие в тело цикла, располагаются начиная от этого описания и до конца документа MathCAD или до конструкции, переопределяющей дискретную переменную – параметр цикла.

Пример 7.2.1. Сформировать вектор z из n элементов, определяемых соотношением:

zi = (i + 4)

В этом примере i – параметр цикла, а тело цикла (вычисление элементов zi ) будет повторено n = 10 раз, т.е. алгоритм является циклом типа арифметической прогрессии. На рис.7.6. показано реше-

ние.

Рис. 7.6. Формирование вектора z

Пример 7.2.2. Сформировать матрицу (двумерный массив) по следующему правилу:

Очевидно, что этот цикл имеет уже два параметра: i – параметр, определяющий номер строки; j – параметр, определяющий номер столбца матрицы. Напомним, что такой цикл называется двойным циклом.

Рис. 7.7. Формирование двумерного массива (матрицы В )

Заметим, что в приведенных на рис. 7.6. и 7.7. фрагментах системная переменная ORIGIN=1.

Программирование итерационных циклов. Для этого исполь-

зуется функция until, записываемая в виде:

until (<выражение. 1>,<выражение. 2>).

Эта функция принимает значение равное выражение. 2 , если выражение. 1 больше или равно 0. Как только выражение. 1 принимает отрицательное значение, функция until принимает значение 0,

и дальнейшее выполнение функции прекращается. Это свойство по-

зволяет применять функцию until для программирования итерационных циклов.

Пример 7.2.3. Вычислить приближенное значение квадратного корня методом Ньютона из числа 64, используя итерационную процедуру:

где ε – заданная точность вычисления корня квадратного. Даже задав конкретные значения a,ε (например, а = 64, ε = 0.01), невозможно априори определить количество повторений цикла.

xT =

Вектор i имеет 13 элементов, тогда как вектор значений х – только 8. Это указывает на то, что когда функция until принимает значение 0, она дальнейшее выполнение функции прекращает.

Задание.

ТЕМА 8. РЕШЕНИЕ УРАВНЕНИЙ

8.1. Символьное решение уравнений

Символьное решение уравнения может осуществляться двумя разными методами:

1. При помощи символьного ключевого слова solve (решить) из панели Символы.

Символьное ключевое слово solve , может быть использовано при решении уравнений или неравенств. Уравнение может содержать пользовательскую функцию. Символьный знак равенства в уравнениях может быть введен из панели Булево или с клавиатуры, печатая 'Ctrl=’. После запятой вводится переменная, значения которой необходимо вычислить.

Пример: вычислите значения x, удовлетворяющие уравнению x3 - 3x - 1 = -1.

Для этого:

•введите выражение левой части уравнения

•вызовите панель символьных вычислений, включив флажок

Вид/Панели инструментов/Символы.

•В появившейся панели нажмите кнопку solve (решить). Получим solve, → .

•Слева от слова solve поле-метка заполнится уравнением, а в позицию справа от слова solve введите имя переменной x, относительно которой нужно решить уравнение.

•Щелкните мышью по свободному месту на листе

Результат будет изображен справа от стрелки, находящейся вслед за именем переменной.

Получим

x3 − 3x − 1 −1 solve,x →

Заметим, что решение представлено столбцом матрицы. Теперь решим неравенство x3 - 3x - 1 > -1

x3 − 3x − 1 > −1 solve,x →

Отметим, что первое решение определяет область значений x при

Второе решение показывает, что область значений x удовлетворяет

условию x > 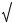3.

Следующий пример показывает как решить квадратное уравнение в общем виде.

Пример 8.1.1