Задачи к экзамену
.docx
Задача 1. Код
Морзе - типичный пример неравномерного
двоичного кода
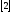 .
В нем символы
.
В нем символы
 и
и
 применяются лишь в двух сочетаниях –
как одиночные (
применяются лишь в двух сочетаниях –
как одиночные ( и
и
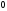 )
или как тройные (
)
или как тройные (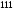 и
и
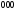 ).
Сигнал, соответствующий
).
Сигнал, соответствующий
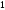 ,
называется точкой, а
,
называется точкой, а
 –
тире. Символ
–
тире. Символ
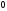 используется как знак, отделяющий точку
от тире, точку от точки и тире от тире.
Совокупность
используется как знак, отделяющий точку
от тире, точку от точки и тире от тире.
Совокупность
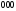 применяется как знак разделения кодовых
слов.
применяется как знак разделения кодовых
слов.
Задача 2. Пусть
алфавит
 источника состоит из символов
источника состоит из символов
 ,
,
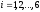 .
Вероятности появления символов на
выходе источника, соответственно, равны
.
Вероятности появления символов на
выходе источника, соответственно, равны
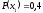 ,
,
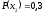 ,
,
 ,
,
 ,
,
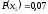 и
и
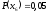 .
Процедура Шеннона-Фано построения
неравномерного кода без укрупнения
алфавита источника задается табл. 1.1
.
Процедура Шеннона-Фано построения
неравномерного кода без укрупнения
алфавита источника задается табл. 1.1
 .
.
Таблица 1.1. Кодирование источника по методу Шеннона-Фано
|
|
|
Выбор символов неравномерного кода |
|
||||
|
1 |
2 |
3 |
4 |
|
|||
|
|
0,4 0,3 0,1 0,08 0,07 0,05 |
0 1 1 1 1 1 |
0 1 1 1 1 |
0 0 1 1 |
0 1 0 1 |
1 2 4 4 4 4 |
|
На
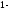 ом
этапе множество символов делим на
ом
этапе множество символов делим на
 части:
части:
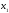 и
и
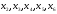 ;
на
;
на
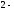 ом
-
ом
-
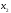 и
и
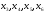 ;
на
;
на
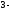 ем
-
ем
-
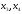 и
и
 ;
на
;
на
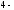 ом
-
ом
-
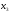 и
и
 ,
,
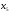 и
и
 .
Более вероятным символам источника
присвоим кодовые слова меньшей длины
.
Более вероятным символам источника
присвоим кодовые слова меньшей длины
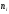 .
Построили префиксный код. Средняя длина
кодового слова (среднее число символов
кода на один символ источника)
.
Построили префиксный код. Средняя длина
кодового слова (среднее число символов
кода на один символ источника)
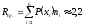 .
.
Задача
3. Каждое
кодовое слово наиболее простого из
линейных систематических двоичных
кодов
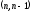 содержит
содержит
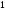 проверочный символ, равный сумме по
проверочный символ, равный сумме по
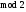 всех информационных символов. Это - код
с проверкой
на четность. Для
него кодовое расстояние
всех информационных символов. Это - код
с проверкой
на четность. Для
него кодовое расстояние
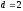 ,
что позволяет гарантированно обнаружить
лишь однократные ошибки. Слова такого
кода имеют только четные веса. Вероятность
пропуска ошибки в
,
что позволяет гарантированно обнаружить
лишь однократные ошибки. Слова такого
кода имеют только четные веса. Вероятность
пропуска ошибки в
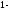 ом
приближении равна вероятности искажения
ом
приближении равна вероятности искажения
 х
символов:
х
символов:
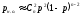 .
.
Есть видоизмененный
способ контроля на четность.
Последовательность информационных
символов
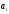 ,
где
,
где
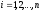 ,
разбивается на
,
разбивается на
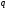 строк по
строк по
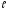 символов в каждой так, что
символов в каждой так, что
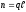 .
Контрольные разряды
.
Контрольные разряды
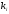 ,
где
,
где
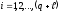 ,
выделены каждой строке и каждому столбцу
по следующей схеме:
,
выделены каждой строке и каждому столбцу
по следующей схеме:
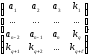
Контроль на четность
делается по строкам и по столбцам. Если,
например, нарушение четности обнаружено
для
 -ой
строки и
-ой
строки и
 -ого
столбца, то символ
-ого
столбца, то символ
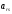 матрицы - ошибочный. Исправление
обнаруженной ошибки достигается заменой
этого символа (
матрицы - ошибочный. Исправление
обнаруженной ошибки достигается заменой
этого символа (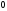 - на
- на
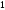 или
или
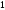 - на
- на
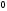 ).
).
Задача 4. Пусть
дискретный источник равновероятно
выдает двоичную цифру
 или
или
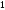 каждые
каждые
 секунд. Количество информации, доставляемое
цифрой,
секунд. Количество информации, доставляемое
цифрой,
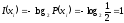 (бит),
(бит),
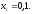 Пусть последовательные цифры на выходе
источника статистически независимы,
то есть источник не имеет памяти. Всего
есть
Пусть последовательные цифры на выходе
источника статистически независимы,
то есть источник не имеет памяти. Всего
есть
 возможных
возможных
 битовых
блоков источника, каждый – с вероятностью
битовых
блоков источника, каждый – с вероятностью
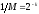 и длительностью
и длительностью
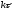 .
Собственная информация блока за время
.
Собственная информация блока за время
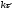 равна
равна
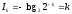 (бит).
(бит).
Определим условную собственную информацию
 (2.3)
(2.3)
где
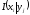 - собственная информация события
- собственная информация события
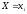 при известном
при известном
 .
.
Комбинируя (2.1), (2.2) и (2.3), получим
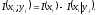 (2.4)
(2.4)
Средняя взаимная
информация случайных величин
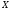 и
и
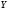 в расчете на символ
в расчете на символ
 (2.5)
(2.5)
где
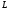 и
и
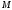 - объемы алфавитов
- объемы алфавитов
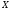 и
и
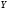 ,
соответственно. Можно показать, что
,
соответственно. Можно показать, что
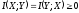 ,
и
,
и
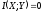 для статистически независимых
для статистически независимых
 и
и
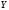 .
.
Средняя условная собственная информация - условная энтропия,
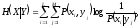 (2.6)
(2.6)
где
 - неопределенность в значениях
- неопределенность в значениях
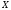 (дополнительная информация, содержащаяся
в
(дополнительная информация, содержащаяся
в
 )
после наблюдения
)
после наблюдения
 .
.
Энтропия источника равна его средней собственной информации на символ,
 (2.7)
(2.7)
Из (2.1), (2.5), (2.6) и (2.7) следует
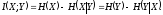 (2.8)
(2.8)
Из (2.8) и
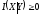 следует
следует
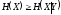 и
и
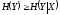 ,
где равенство верно, если
,
где равенство верно, если
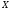 статистически не зависит от
статистически не зависит от
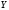 .
Величина
.
Величина
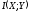 равна уменьшению среднего значения
неопределенности значений
равна уменьшению среднего значения
неопределенности значений
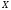 (
(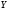 )
за счет измерения
)
за счет измерения
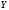 (
(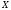 ).
Пусть
).
Пусть
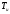 - длительность символа источника.
Производительность
источника
- среднее количество информации,
выдаваемое им в единицу времени,
- длительность символа источника.
Производительность
источника
- среднее количество информации,
выдаваемое им в единицу времени,
 (2.9)
(2.9)
Задача 5. Возьмем
источник, выдающий последовательность
независимых символов:
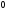 - с вероятностью
- с вероятностью
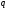 ,
и
,
и
 - с вероятностью
- с вероятностью
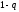 .
Энтропия двоичного источника
.
Энтропия двоичного источника
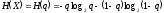 .
Максимальное значение
.
Максимальное значение
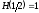 бит (при равновероятных символах), а
минимальное -
бит (при равновероятных символах), а
минимальное -
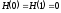 (если возможна передача лишь одного
символа).
(если возможна передача лишь одного
символа).
Для источника с
объемом алфавита
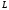 выразим
выразим
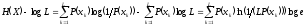 .
.
Так как
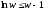 (
(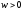 ),
то
),
то
 ,
или
,
или
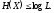 (2.10)
(2.10)
Наибольшее значение:
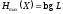 (информационная
емкость алфавита
источника), достигается, если символы
равновероятны:
(информационная
емкость алфавита
источника), достигается, если символы
равновероятны:
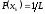 ,
,
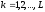 .
Для передачи количества информации
.
Для передачи количества информации
 от источника с энтропией
от источника с энтропией
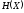 требуется
требуется
 символов, а от источника с энтропией
символов, а от источника с энтропией
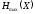 - минимальное их число
- минимальное их число
 (2.11)
(2.11)
где
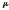 - допустимая
степень сжатия сообщений,
- допустимая
степень сжатия сообщений,
 .
Величина
.
Величина
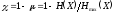 называется избыточностью
источника.
называется избыточностью
источника.
Пусть есть блок
из
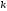 случайных величин
случайных величин
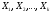 с совместной вероятностью
с совместной вероятностью
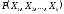 .
Пусть
.
Пусть
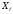 ,
,
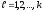 ,
имеет алфавит
,
имеет алфавит
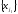 ,
,
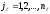 ,
с объемом
,
с объемом
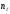 .
Энтропия этого блока, согласно (2.7),
.
Энтропия этого блока, согласно (2.7),
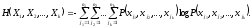 (2.12)
(2.12)
Так как
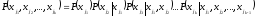 ,
из (2.12) следует
,
из (2.12) следует
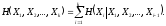 (2.13)
(2.13)
Так как
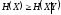 ,
где
,
где
 и
и
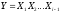 ,
из (2.13) имеем:
,
из (2.13) имеем:
 (2.14)
(2.14)
где равенство
верно, если
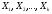 не зависят друг от друга.
не зависят друг от друга.
Задача 6 . Из
(2.17)
выразим
дифференциальную энтропию гауссовской
величины
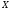 с распределением
с распределением
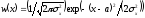 ,
средним
,
средним
 и дисперсией
и дисперсией
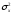 :
:
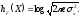 (2.18)
(2.18)
При заданной
дисперсии среди случайных непрерывных
величин с разными законами распределения
наибольшую дифференциальную энтропию
имеет гауссовская величина
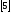 .
.
Условная
дифференциальная энтропия
случайной непрерывной величины
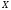 при заданной
при заданной
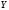 :
:
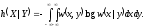 (2.19)
(2.19)
Учитывая (2.16),
(2.17) и (2.19),

 ,
найдем
,
найдем
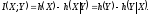 (2.20)
(2.20)
Задача 7. Пусть
случайная величина
 ,
где
,
где
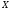 и
и
 - независимые гауссовские величины с
дисперсией
- независимые гауссовские величины с
дисперсией
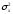 и
и
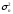 ,
соответственно. Рассмотрим
,
соответственно. Рассмотрим
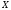 и
и
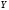 как амплитуды импульсов на входе и
выходе канала, соответственно, а
как амплитуды импульсов на входе и
выходе канала, соответственно, а
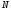 - как аддитивный шум, добавляющийся к
импульсам при передаче по каналу.
Согласно центральной
предельной теореме
теории вероятностей (ЦПТ)
- как аддитивный шум, добавляющийся к
импульсам при передаче по каналу.
Согласно центральной
предельной теореме
теории вероятностей (ЦПТ)
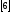 ,
величина
,
величина
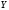 - тоже гауссовская с дисперсией
- тоже гауссовская с дисперсией
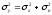 .
С учетом (2.18) ее дифференциальная энтропия
равна
.
С учетом (2.18) ее дифференциальная энтропия
равна
 .
Из (2.19) следует
.
Из (2.19) следует
 .
Но
.
Но
 и
и
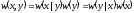 ,
так что условная дифференциальная
энтропия
,
так что условная дифференциальная
энтропия
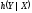 гауссовской величины
гауссовской величины
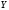 зависит лишь от дисперсии шума
зависит лишь от дисперсии шума
 :
:
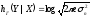 .
Выражения для
.
Выражения для
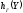 и
и
 подставим в (2.20). Найдем среднюю взаимную
информацию для изучаемого канала:
подставим в (2.20). Найдем среднюю взаимную
информацию для изучаемого канала:
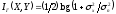 .
При введенных ограничениях
.
При введенных ограничениях
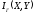 - максимально возможное количество
информации об отсчете входного в канал
сообщения в одном отсчете выходного
сообщения.
- максимально возможное количество
информации об отсчете входного в канал
сообщения в одном отсчете выходного
сообщения.
Задача 8.
Пусть
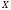 и
и
 - случайные двоичные
- случайные двоичные
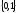 величины на входе и выходе канала. Пусть
входные символы равновероятны. Условные
вероятности выходных символов при
известном входе заданы как
величины на входе и выходе канала. Пусть
входные символы равновероятны. Условные
вероятности выходных символов при
известном входе заданы как
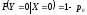 ,
,
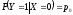 ,
,
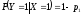 и
и
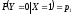 .
Найдем, сколько информации об
.
Найдем, сколько информации об
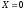 и
и
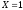 содержит событие
содержит событие
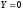 :
:
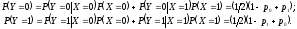
Взаимная
информация о символе
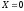 при наблюдении
при наблюдении
 равна
равна

Взаимная
информация о символе
 при наблюдении
при наблюдении
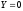 равна
равна
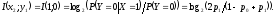
Для
канала без
шумов
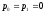 ,
так что
,
так что
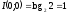 бит. Значит, если выход точно определяет
вход, нет потери информации. При обрыве
канала
бит. Значит, если выход точно определяет
вход, нет потери информации. При обрыве
канала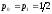 ,
так что
,
так что
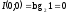 - канал непригоден.
- канал непригоден.
Пусть
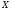 - сообщение источника в канал, а
- сообщение источника в канал, а
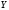 -
сообщение, принимаемое приемником.
Тогда
-
сообщение, принимаемое приемником.
Тогда
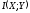 в (2.8) - среднее количество информации,
получаемое приемником с приходом
символа, а ненадежность
в (2.8) - среднее количество информации,
получаемое приемником с приходом
символа, а ненадежность
 - среднее количество информации, теряемое
в канале связи. Шумовая
энтропия
- среднее количество информации, теряемое
в канале связи. Шумовая
энтропия
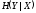 зависит лишь от помех в канале. Пусть
зависит лишь от помех в канале. Пусть
 - среднее время передачи символа по
каналу. Среднее количество информации,
передаваемое по каналу в единицу времени,
- скорость
передачи информации по каналу
- среднее время передачи символа по
каналу. Среднее количество информации,
передаваемое по каналу в единицу времени,
- скорость
передачи информации по каналу
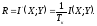 (3.4)
(3.4)
Задача
9. Согласно
(2.6) и (3.1), в
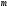 -ичном
симметричном канале без памяти условная
энтропия
-ичном
симметричном канале без памяти условная
энтропия
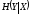 не зависит от передаваемых символов:
не зависит от передаваемых символов:
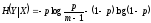 .
Максимальное значение энтропии
.
Максимальное значение энтропии
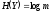 при равновероятных символах
при равновероятных символах
 (см. (2.10)). Выражения для
(см. (2.10)). Выражения для
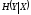 и
и
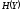 подставим в (2.8). С учетом (3.10) пропускная
способность изучаемого канала
подставим в (2.8). С учетом (3.10) пропускная
способность изучаемого канала
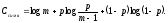 (3.11)
(3.11)
Из
(3.11) видно, что минимальное значение
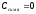 при
при
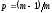 .
Тогда, согласно (3.1),
.
Тогда, согласно (3.1),
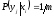 ,
так что каждый входной символ равновероятно
переходит в любой выходной. Наблюдая
выходные символы, нельзя предпочесть
ни один из входных. Это означает обрыв
канала -
передача информации по каналу бесполезна.
Тот же результат следует при случайном
угадывании входных символов в точке
приема. Из (3.11) для двоичного канала
максимальное значение
,
так что каждый входной символ равновероятно
переходит в любой выходной. Наблюдая
выходные символы, нельзя предпочесть
ни один из входных. Это означает обрыв
канала -
передача информации по каналу бесполезна.
Тот же результат следует при случайном
угадывании входных символов в точке
приема. Из (3.11) для двоичного канала
максимальное значение
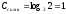 бит и при
бит и при
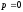 ,
и при
,
и при
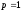 .
Случай
.
Случай
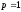 описывает состояние канала с обратной
работой.
Тогда при передаче по каналу все
описывает состояние канала с обратной
работой.
Тогда при передаче по каналу все
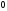 переходят в
переходят в
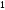 ,
а
,
а
 - в
- в
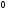 .
Если это заранее известно, при
.
Если это заранее известно, при
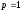 сообщение декодируют по правилу:
сообщение декодируют по правилу:
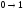 ,
,
 .
.
Из
(2.8), (2.10) и (3.10) найдем пропускную способность
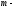 ичного
канала с памятью и аддитивным шумом:
ичного
канала с памятью и аддитивным шумом:
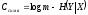 .
Величина
.
Величина
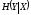 - степень неопределенности в значениях
- степень неопределенности в значениях
 (дополнительная информация в
(дополнительная информация в
 )
при известном
)
при известном
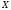 .
За счет памяти канала эта степень
становится меньше, а пропускная
способность – больше
.
За счет памяти канала эта степень
становится меньше, а пропускная
способность – больше
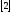 .
.
Задача 10. Возьмем
ДИБП с символами
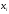 ,
,
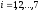 ,
имеющими заданные вероятности выбора.
Надо построить двоичный код (
,
имеющими заданные вероятности выбора.
Надо построить двоичный код (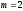 ).
).
Построим кодовое
дерево (см. рис. 4.1). Символы источника
расположим в порядке убывания их
вероятностей. Пусть
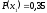 ,
,
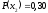 ,
,
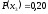 ,
,
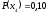 ,
,
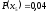 ,
,
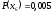 и
и
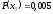 .
Кодирование начнем с
.
Кодирование начнем с
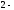 х
наименее вероятных символов
х
наименее вероятных символов
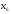 и
и
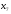 .
Их объединим (см. рис. 4.1). Верхнему
ветвлению присвоим кодовый символ
.
Их объединим (см. рис. 4.1). Верхнему
ветвлению присвоим кодовый символ
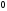 ,
а нижнему -
,
а нижнему -
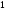 .
Сложим вероятности этих ветвей. Общему
узлу присвоим суммарную вероятность
.
Сложим вероятности этих ветвей. Общему
узлу присвоим суммарную вероятность
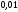 .
Теперь есть исходные символы:
.
Теперь есть исходные символы:
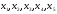 ,
и новый символ
,
и новый символ
 ,
полученный объединением
,
полученный объединением
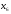 и
и
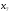 .
На следующем этапе снова объединим
.
На следующем этапе снова объединим
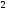 наименее вероятных символа
наименее вероятных символа
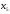 и
и
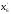 с суммарной вероятностью
с суммарной вероятностью
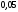 из набора:
из набора:
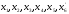 .
Переходу от символа
.
Переходу от символа
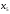 присвоим кодовый символ
присвоим кодовый символ
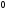 ,
а переходу от символа
,
а переходу от символа
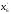 -
-
 .
Процедуру продолжим, пока не исчерпаем
все возможные символы источника.
Результат – кодовое дерево с ветвями,
содержащими искомые кодовые слова.
.
Процедуру продолжим, пока не исчерпаем
все возможные символы источника.
Результат – кодовое дерево с ветвями,
содержащими искомые кодовые слова.
Кодовые слова (см.
табл. 4.1) получаются, если двигаться от
самого правого узла дерева, переходя к
самому левому узлу. Среднее число кодовых
символов на символ источника
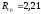 бит/символ, а энтропия источника -
бит/символ, а энтропия источника -
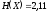 бит/символ.
бит/символ.
0,35
0,30
0,20
0,10
0,04
0,005
0,005
Рис. 4.1. Построение кодового дерева
Таблица 4.1. Кодовые слова кода Хаффмена и их характеристики
|
Символ |
Вероятность |
Собственная информация |
Код |
|
|
0,35 |
1,5146 |
00 |
|
|
0,30 |
1,7370 |
01 |
|
|
0,20 |
2,3219 |
10 |
|
|
0,10 |
3,3219 |
110 |
|
|
0,04 |
4,6439 |
1110 |
|
|
0,005 |
7,6439 |
11110 |
|
|
0,005 |
7,6439 |
11111 |
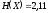
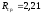
На
предпоследнем шаге процедуры кодирования
был равный по вероятности выбор между
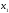 и
и
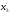 .
Здесь были соединены
.
Здесь были соединены
 и
и
 .
Вместо этого в альтернативном коде
можно было бы соединить
.
Вместо этого в альтернативном коде
можно было бы соединить
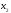 и
и
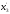 ,
получив символ
,
получив символ
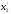 .
На последнем шаге построения кодового
дерева соединялись бы символы
.
На последнем шаге построения кодового
дерева соединялись бы символы
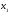 и
и
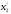 .
Для альтернативного кода среднее число
битов на символ тоже равно
.
Для альтернативного кода среднее число
битов на символ тоже равно
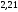 ,
как и для кода на рис. 4.1. То есть, полученные
коды одинаково эффективны. Назначение
,
как и для кода на рис. 4.1. То есть, полученные
коды одинаково эффективны. Назначение
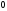 верхнему переходу и
верхнему переходу и
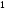 - нижнему (менее вероятному) переходу,
выбрано произвольно. Поменяв местами
- нижнему (менее вероятному) переходу,
выбрано произвольно. Поменяв местами
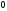 и
и
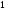 ,
получим еще два эффективных префиксных
кода.
,
получим еще два эффективных префиксных
кода.
Задача 11.
Возьмем гауссовский источник без памяти
с ФПВ
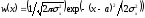 ,
математическим ожиданием
,
математическим ожиданием
 и дисперсией
и дисперсией
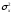 .
Из (5.1) для среднеквадратичной ошибки
на символ (
.
Из (5.1) для среднеквадратичной ошибки
на символ (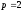 )
в качестве меры искажения
)
в качестве меры искажения
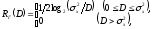
где при
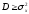 никакой информации передавать не надо.
никакой информации передавать не надо.
Задача 12.
Оптимальный
 уровневый
(
уровневый
(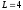 )
неравномерный квантователь для
гауссовской амплитуды сигнала с нулевым
средним и единичной дисперсией, согласно
(5.3), описан в табл. 5.2.
)
неравномерный квантователь для
гауссовской амплитуды сигнала с нулевым
средним и единичной дисперсией, согласно
(5.3), описан в табл. 5.2.
Таблица 5.2. Уровни
оптимального
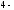 уровневого
неравномерного квантователя
уровневого
неравномерного квантователя
|
Уровень
|
|
1 -0,9816 -1,510 2 0,0 -0,4528 3 0,9816 0,4528 4
|
|
|
Вероятности
символов на выходе квантователя:
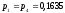 - для двух внешних уровней и
- для двух внешних уровней и
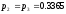 - для двух внутренних уровней. Тогда
энтропия дискретного источника
- для двух внутренних уровней. Тогда
энтропия дискретного источника
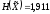 бит/символ.
бит/символ.
Квантователь
превращает непрерывную амплитуду
источника в дискретную. Дискретные
амплитуды трактуем как символы
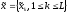 с вероятностями
с вероятностями
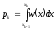 .
Выход квантователя можно подвергнуть
энтропийному кодированию для повышения
эффективности сжатия данных. При
независимых отсчетах амплитуды сигнала
на выходе квантователя получим дискретный
источник без памяти с энтропией
.
Выход квантователя можно подвергнуть
энтропийному кодированию для повышения
эффективности сжатия данных. При
независимых отсчетах амплитуды сигнала
на выходе квантователя получим дискретный
источник без памяти с энтропией
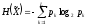 .
.
Задача 13. У систематического кода с порождающей матрицей

кодовое слово -
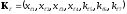 ,
где
,
где
 -
-
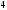 информационных бита,
информационных бита,
 -
-
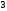 проверочных бита,
проверочных бита,
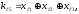
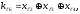 и
и
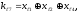 Кодер для этого кода
Кодер для этого кода
 показан на рис. 6.1.
показан на рис. 6.1.
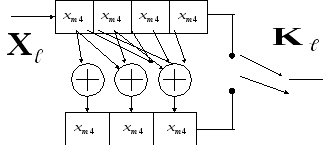

Рис.
6.1 Схема кодера блокового линейного
кода
Для любого линейного
кода
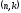 существует дуальный
(двойственный)
код
существует дуальный
(двойственный)
код
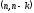 .
Любое кодовое слово
.
Любое кодовое слово
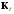 кода
кода
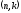 ортогонально любому кодовому слову
дуального кода. Порождающая матрица
ортогонально любому кодовому слову
дуального кода. Порождающая матрица
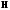 размерности
размерности
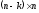 дуального кода имеет
дуального кода имеет
 линейно независимых векторов-строк,
причем
линейно независимых векторов-строк,
причем
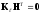 ,
(6.2)
,
(6.2)
где
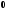 - вектор-столбец из
- вектор-столбец из
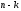 нулей. В частности,
нулей. В частности,
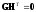 ,
где
,
где
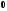 - матрица из нулей размерности
- матрица из нулей размерности
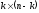 .
Для систематического кода с порождающей
матрицей
.
Для систематического кода с порождающей
матрицей
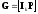 дуальный код имеет порождающую матрицу
дуальный код имеет порождающую матрицу

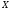

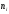
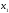
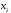
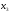
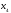

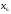
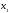
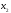
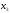


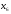

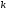
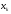
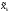
 1,510
1,510