1 семестр / Определённые интегралы. Кленина

Переходя к пределу в каждой интегральной сумме I и In , имеем

Получили, что значение предела интегральной суммы I nlim In

n

lim f ci xi зависит от выбора точек ci xi 1,xi a,b , следова-

n i 10

b

тельно не существует nlim In , а значит и не существует f x dx для

a

функции Дирихле f x .

Утверждение. Неограниченная на отрезке a,b функция y f x

не интегрируема на этом отрезке.

Доказательство. Пусть T – такое разбиение отрезка a,b , в кото-

i 1

разбиения T может быть сколь угодно большим по абсолютной величине за счет выбора точки c j Îéêëx j-1,x j ùúû . Поэтому не существует конеч-

b

ного предела функция y = f (x), а значит и интеграла f x dx .

a

11

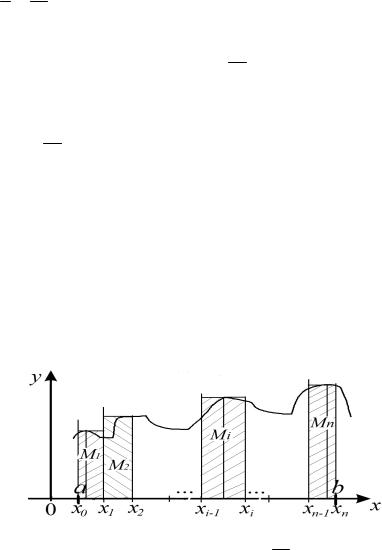
1.2. Геометрический смысл определенного интеграла

Пусть на отрезке a,b задана непрерывная неотрицательная функция y f x .

Геометрический смысл определенного интеграла от неотрицатель-

ной функции состоит в том, что определенный интеграл численно равен площади криволинейной трапеции. Покажем это.

Разобьем отрезок a,b на n частей с помощью точек

x0 a,x1,x2. ,xn b .

Функция y f x достигает своего наибольшего и наименьшего

значения на каждом отрезке x0,x1 , x1,x2 , , xi 1,xi , , xn 1,xn . Пусть M1,M2, ,Mi , ,Mn – наибольшие значения функции на каж-

дом отрезке x0,x1 , x1,x2 , , xi 1,xi , , xn 1,xn соответственно. По-

строим сумму S Sn M1 x1 M2 x2 Mi xi M n xn (см. рис. 1.3), которая называется верхней суммой функции y f x для полученного

разбиения отрезка a,b . Верхняя сумма Sn равна площади, заштрихо-

ванной части на рис. 1.3 ступенчатой фигуры, которая содержит криволинейную трапецию.

Множество Sn верхних сумм заданной функции y f x для всевозможных разбиений отрезка a,b является ограниченным снизу.

Пусть m1,m2, ,mi , ,mn – наименьшие значения функции на каж-

дом отрезке x0,x1 , x1,x2 , , xi 1,xi , , xn 1,xn соответственно. Построим сумму s sn m1 x1 m2 x2 mi xi mn xn (см. рис. 1.4),

которая называется нижней суммой функции y f x для полученного разбиения отрезка a,b .

Рис. 1.3. Разбиение криволинейной трапеции для построения верхней суммы Sn

12

Нижняя сумма sn равна площади, заштрихованной части на рис. 1.4 ступенчатой фигуры, которая содержится в криволинейной трапеции.

Рис. 1.4. Разбиение для построения нижней суммы sn

Следовательно, множество sn нижних сумм заданной функции

y f x для всевозможных разбиений отрезка a,b является ограни-

ченным сверху.

Верхняя и нижняя сумма зависят от n – числа разбиений отрезкаa,b . Верхняя Sn и нижняя sn суммыобладаютследующими свойствами.

Для верхней Sn , нижней sn и интегральной In сумм справедливо неравенство sn In Sn .

Для функции y f x на любом отрезке xi 1,xi выполняются не-

i 1,2, ,n можно выбрать так, что интегральная сумма будет удовле-

творять неравенствам 0 Sn In и 0 In sn i 1,2, ,n . Доказательство. Пусть T – фиксированное разбиение отрезка

a,b . Для функции y f x на любом отрезке xi 1,xi выполняются неравенство mi f ci Mi для произвольно выбранных тачек ci , гдеMi и mi – наибольшее и наименьшее значения функции y f x на отрезкеxi 1,xi . Для любого числа 0 промежуточные точки ci на отрезкахxi 1,xi i 1,2, ,n можно выбрать так, чтобы имело место неравен-

ство 0 Mi f ci b a .

13

Умножим каждое из этих неравенств на длину соответствующего отрезка и сложим полученные произведения, получим

i 1

ную сумму In . Получили одно из требуемых неравенств: 0 Sn In . Аналогично, для заданного числа 0 промежуточные точки ci на отрезках xi 1,xi i 1,2, ,n можно выбрать так, чтобы имело место

неравенство 0 f ci mi b a . Умножим каждое из этих неравенств на длину соответственного отрезка и, складывая полученные произведе-

i 1

сумму In .

Получили одно из требуемых неравенств: 0 In sn , что и требо-

валось.

Свойство 2. Если разбиение T отрезка получено путем добавления

новых точек к точкам разбиения T этого отрезка, то верхняя сумма Sk

разбиения T , а именно: sk sn .

Другими словами: при увеличении числа отрезков, на которые разбивается заданный отрезок a,b путем добавления новых точек деления,

нижняя сумма sn может только возрастать, а верхняя сумма Sn – только убывать.

14

Доказательство. Разбиение T может быть получено из разбиения T путем последовательного добавления к разбиению T новых точек, поэтому сформулированное свойство достаточно доказать для случая, когда к разбиению T добавляется одна точка (см. рис. 1.5). Пусть эта точка x xi 1,xi разбиения T отрезка a,b .

отрезках x0,x1 , x1,x2 , , xi 1,xi , , xn 1,xn .

частями отрезка xi 1,xi и не превосходят наибольшего значения Mi функции y f x на всем отрезке xi 1,xi . Так как Sn (верхняя сумма

Заменяем xi xi xi и группируем, вынося общий множитель,

получаем Sn Sn 1 Mi Mi xi Mi Mi x 0.

15

Тогда Sn Sn 1 0 или Sn 1 Sn , то есть при добавлении новых точек деления на отрезке a,b верхняя сумма Sn – убывает. Доказательство того, что при добавлении новых точек деления на отрезке a,b нижняя сумма sn возрастает, проводится аналогично.

Свойство 3. Пусть T и T – любые два разбиения отрезка a,b . Тогда нижняя сумма одного из этих разбиений не превосходит верхнюю

сумму другого разбиения. Именно, если s , S и s , S – нижние и верхние суммы разбиений T и T соответственно, то выполняются неравен-

sn In Sn . Отсюда делаем вывод, что нижняя сумма заданного разбие-

ния не превосходит верхнюю сумму этого же разбиения, а именно,

sn Sn .

Пусть T – разбиение отрезка a,b , полученное объединением раз-

биений T и T , причем общие точки разбиений T и T учитываются один раз. Разбиение T может быть получено из разбиения T путем до-

бавления к нему точек разбиения T . Обозначим S и s – верхнюю и нижнюю суммы разбиения T соответственно.

Учитывая свойство 2 и то, что если s и S – соответственно ниж-

ние и верхние суммы разбиения T , получаем s s S S .

Но разбиение T можно рассматривать, как разбиение T путем добавления к нему точек разбиения T , тогда по свойству 2, учитывая

что s и S – соответственно нижние и верхние суммы разбиения T , имеем s s S S .

Сравнивая последние два неравенства, получаем s s S S и s s S S .Следовательно, s S и s S ,чтоитребовалосьдоказать.

Свойство 4. Множество S верхних сумм данной функции y f x для всевозможных разбиений отрезка a,b ограничено снизу, а множество s нижних сумм ограничено сверху.

16

Доказательство. Из свойства 3 следует, что S s и S s , то есть любая верхняя сумма заданной функции y f x не меньше неко-

торой фиксированной нижней суммы. Следовательно, множество S верхних сумм ограничено снизу.

Аналогично, из свойства 3 следует: s S и s S , то есть любая

нижняя сумма заданной функции y f x не превосходит некоторой фиксированной верхней суммы. Следовательно, множество s нижних сумм ограничено сверху.

j 1,2, ,n,n 1, стремятся к некоторым пределам s и S соответ-

ственно, а именно существуют lim sn s и lim Sn S .

n n

Доказательство. Последовательность sn является неубываю-

щей, то есть при добавлении новых точек деления на отрезке a,b для нижних сумм выполняется неравенство sn sn 1 (свойство 2). Кроме того

последовательность sn является ограниченной сверху (свойство 4).

По известной теореме Вейерштрасса (см, например, [9], с.71, теорема 3.15): всякая неубывающая последовательность ограниченная сверху имеет предел, следовательно, существует nlim sn s .

Аналогично, последовательность Sn является невозрастающей, то есть при добавлении новых точек деления на отрезке a,b для верхних сумм выполняется неравенство Sn Sn 1 (свойство 2).

Кроме того последовательность Sn является ограниченной снизу

(свойство 4).

По известной теореме Вейерштрасса (см., например, [9], с.71, теорема 3.15): всякая невозрастающая последовательность, ограниченная

снизу, имеет предел, следовательно, существует lim Sn S . Свойство 5

n

доказано.

17

Свойство 6. Для непрерывной функции y f x на замкнутом от-

Теорема. Для того чтобы ограниченная на отрезке a,b функция y f x была интегрируема на этом отрезке, необходимо и достаточно, чтобы для любого 0 нашлось такое разбиение T отрезка a,b , для

которого выполняется неравенство S s .

Доказательство. Необходимость. Пусть функция y f x явля-

ется интегрируемой на отрезке a,b ,то есть существует интегралфункции y f x ,какконечныйпределпоследовательностиинтегральныхсумм:

18

где S , s – верхняя и нижняя суммы разбиения T . Построим две новые интегральные суммы. Для этого выберем на каждом отрезке

i 1

ки выберем так, чтобы выполнялись неравенства:

S s S In In In In In In s .

19

Согласно свойству 1 для любого фиксированного разбиения T и

0 In s 3 i 1,2, ,n .

Известны теоремы о предельном переходе в неравенствах

(см., например, [9], с.68, теорема 3.13): если элементы сходящейся последовательности In , начиная с некоторого номера n , удовлетворяет

нюю S суммы, а также используя свойство модуля.

n N следует In I .Достаточностьдоказанаиснейдоказанатеорема. Сформулируем эквивалентную теорему о необходимом и доста-

и наименьшее значения функции y f x соответственно, на отрезке

xi 1,xi a,b .

Отметим, что колебание функции y f x на отрезке xi 1,xi является неотрицательным числом, так как на каждом отрезке xi 1,xi выполняется неравенство Mi mi , i 1,2,3, ,n .

20