
Поташев
.pdfКАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Памяти профессора Владимира Васильевича Клокова
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО МЕХАНИКЕ СПЛОШНОЙ СРЕДЫ
Учебно-методическое пособие
Казань - 2010
УДК 531.01
Печатается по решению Редакционно-издательского совета ФГАОУВПО «Казанский (Приволжский) федеральный университет»
методической комиссии механико-математического факультета Протокол № 2 от 26 ноября 2010 г.
заседания кафедры аэрогидромеханики Протокол № 1 от 28 октября 2010 г.
Составитель
канд. физ.-мат. наук, К.А. Поташев
Рецензент
канд. физ.-мат. наук, доц. Е.И. Филатов
Практические занятия по механике сплошной среды: Учебно-
методическое пособие / К.А. Поташев. – Казань: Казанский университет, 2010. – 44 с.
Учебно-методическое пособие предназначено для использования студентами и преподавателями механико-математического факультета при изучении и изложении курса механики сплошной среды. Пособие содержит набор задач по основам тензорного исчисления и их приложениям к задачам механики. Материал изложен в форме отдельных занятий, состоящих из перечня основных формул и определений, примеров решения типовых задач и набора дополнительных заданий.
© Казанский университет, 2010
3
СОДЕРЖАНИЕ |
|
ЗАНЯТИЕ 1. Криволинейные координаты. Базисные векторы. Метрическая |
|
матрица. Сопряженный базис ................................................................................. |
5 |
ЗАНЯТИЕ 2. Преобразование координат. Инвариантные объекты ................. |
11 |
ЗАНЯТИЕ 3. Операции над тензорами. Физические компоненты вектора..... |
16 |
ЗАНЯТИЕ 4. Альтернирование и симметрирование. Тензорная поверхность, |
|
главные значения и главные направления........................................................... |
19 |
ЗАНЯТИЕ 5. Дифференцирование вектора и тензора по координате ............. |
23 |
ЗАНЯТИЕ 6. Основные дифференциальные операторы ................................... |
27 |
ЗАНЯТИЕ 7. Лагранжево и эйлерово описание сплошной среды. |
|
Материальная производная по времени .............................................................. |
31 |
ЗАНЯТИЕ 8. Приложения к механике. Перемещение. Деформация ............... |
34 |
ЗАНЯТИЕ 9. Приложения к механике. Напряжения. Уравнения равновесия 39 |
|
Справочный материал............................................................................................ |
43 |
Литература .............................................................................................................. |
44 |
4
ЗАНЯТИЕ 1. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ. БАЗИСНЫЕ ВЕКТОРЫ. МЕТРИЧЕСКАЯ МАТРИЦА.
СОПРЯЖЕННЫЙ БАЗИС
Основные формулы и определения
Соглашение о суммировании (правило суммирования Эйнштейна): при наличии у некоторого одночлена двух индексов, обозначенных одной и той же буквой и расположенных один вверху (контравариантный индекс), а другой внизу (ковариантный индекс), предполагается суммирование по всем значениям, которые может принимать данный индекс (для трехмерного пространства – от единицы до трех). Индексы, по которым осуществляется суммирование, называются немыми индексами (так как их буквенное обозначение не влияет на результат). Например:
3
aibi = ∑aibi = a1b1 + a2b2 + a3b3 .
i=1
Координатной поверхностью xi = const называют геометрическое место точек, для которых указанная координата постоянна. Например, в координатной плоскости yOz декартовой прямолинейной системы координата x ее точек постоянна и равна нулю.
Координатной линией называют геометрическое место точек, для которых одна и только одна координата переменна. Координатные линии – пересечения координатных поверхностей.
Если координатные линии прямолинейны, то система координат называется прямолинейной. В противном случае система координат является криво-
линейной.
Базисные векторы Эi (или векторы базиса) по определению равны
|
|
|
|
(x |
i |
i |
, x |
j |
, x |
k |
|
i |
, x |
j |
, x |
k |
) |
|
Э = |
∂ r |
= |
lim |
r |
|
+ x |
|
|
) − r |
(x |
|
|
||||||
∂ xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
i |
|
xi →0 |
|
|
|
|
|
xi |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x j , xk =const
направлены по касательным к координатным линиям в данной точке в сторону возрастания соответствующей координаты (индексы i, j, k могут принимать значения 1, 2, 3 и расположены в циклическом порядке). Концы векто-
ров, стоящих в числителе дроби, лежат на координатной линии xi .
В отличие от прямолинейных координатных систем в криволинейных системах координат векторы не являются свободными, так как направления и, вообще говоря, величины базисных векторов зависят от точки приложения.
Метрическая матрица
5
g |
g |
g |
|
= (g |
|
) |
g11 |
g12 |
g13 |
|
ij |
||
21 |
22 |
23 |
|
|
|
|
g31 |
g32 |
g33 |
|
|
|
|
позволяет выразить квадрат расстояния между парой бесконечно близких точек в виде:
ds2 = g |
ij |
dxi dx j . |
(1.1) |
|
|
|
Компоненты метрической матрицы могут быть вычислены как скалярное произведение базисных векторов:
gij = Эi × Эj .
Сопряженной матрицей или обратной к метрической матрице ( gij ) на-
зывается матрица (gij ), если элементы этих двух матриц связаны следующим образом:
gij g jk = δik или g jk = G jk* g ,
g ,
где G jk* – элементы транспонированной матрицы (G jk ); G jk – алгебраиче-
ское дополнение к элементу g jk , g = 
 gij
gij 
 – определитель матрицы (gij ).
– определитель матрицы (gij ).
G jk = A jk (-1) j +k , A jk – миноры к элементу g jk , δi j – символ Кронекера, определяемый как
|
δi j = 1, |
i = j . |
||
|
|
|
{0, |
i ¹ j |
Сопряженный (обратный, контравариантный) базис векторов Э j опре- |
||||
деляется выражением: |
|
|
|
|
|
|
Э j = g ji Э . |
||
|
|
|
|
i |
Величины с нижней индексацией называются КОвариантными, с верх- |
||||
ней индексацией – КОНТРАвариантными. |
||||
Примеры решения задач |
|
|
|
|
Задача 1.1. Дать развернутую запись выражений Miiiiiα ; aiδi j ; δii ; aα bα j . |
||||
Решение. |
|
|
|
|
1. M1iii1α + M 2i2iiα + M3i3iiα , индекс α – |
свободный (по нему нет суммирования); |
|||
a1, |
j =1 |
|
||
|
2 , |
|
= a j ; |
|
2. aiδi j = a1δ1j + a2δ2j + a3δ3j = a |
j = 2 |
|||
|
3 |
, |
|
|
a |
|
j = 3 |
|
|
6
3. δ 1 |
+ δ 2 |
+ δ 3 |
= 3; |
4. a1b |
+ a2b |
+ a3b |
. |
1 |
2 |
3 |
|
1 j |
2 j |
3 j |
|
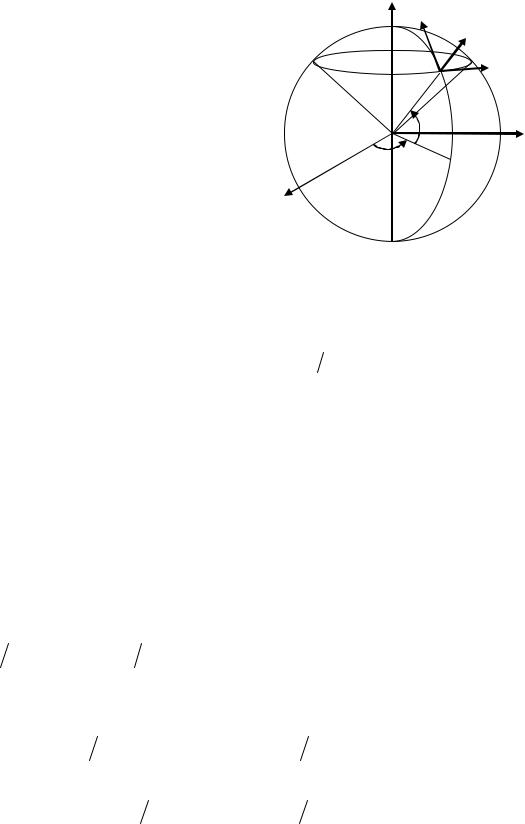
Задача 1.2. Определить координатные поверхности и координатные линии сферической системы координат r,ϕ, λ . Показать, что касательные к координатным линиям в точке M сферической системы координат взаимно перпендикулярны.
Решение. |
Используем |
обозначения |
x |
x1 = r , x2 = ϕ , |
x3 = λ (рис. 1). |
Координатная |
z |
Э3 Э1 |
|
M Э2 x1
x3
y
x2
поверхность x1 = const – сфера радиуса r = x1
с центром в точке O ; координатная поверх- |
Рис. 1 |
|
ность x2 = const – полуплоскость, |
проходящая через ось Oz и точку M ; ко- |
|
ординатная поверхность x3 = const |
– коническая поверхность, ось симметрии |
|
которой – Oz , образующая, составляет с осью угол π 2 − x3 . |
||
Координатная линия x1 – луч, проходящий через O и M ; координатная |
||
линия x2 – окружность радиуса |
x1 cos x3 , |
плоскость которой параллельна |
xOy ; координатная линия x3 – полуокружность радиуса x1 , лежащая в координатной плоскости x2 = const .
Касательные лежат во взаимно перпендикулярных плоскостях, следовательно, они взаимно перпендикулярны.
Задача 1.3. Определить модули векторов базиса введенной сферической
системы координат в точке M . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Э |
|
= |
lim |
|
r |
x1 |
|
|
= lim |
|
x1 |
x1 |
|
= 1, здесь r = MN , где M и N - точки, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
x1 →0 |
|
|
|
|
|
|
|
x1 →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x2 , x3 =const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
лежащие на координатной линии x1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
Э |
|
= |
lim |
|
r x2 |
|
|
= |
lim |
|
|
x1 cos x3 x2 |
x2 |
|
= |
|
|
|
x1 cos x3 |
|
, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
x2 →0 |
|
|
|
|
|
|
|
|
|
x2 →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
x1 , x3 =const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
Э |
|
= |
|
lim |
|
r |
x3 |
|
|
= lim |
|
x1 x3 |
x3 |
|
|
|
= |
|
x1 |
|
. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
x3 →0 |
|
|
|
|
|
|
|
|
|
|
x3 →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x1 , x2 =const
7

Задача 1.4. Найти компоненты gij в произвольной точке для сферической
системы координат. Записать компоненты сопряженной метрической матрицы.
Решение. Запишем выражение длины внутренней диагонали прямоугольного параллелепипеда, сторонами которого являются dx1 , x1 cos x3 dx2 ,
x1 dx3 :
ds2 = (dx1 )2 + (x1 cos x3 dx2 )2 + (x1 dx3 )2 .
Сравнивая полученное соотношение с выражением (1.1), получаем матрицу:
|
1 |
0 |
0 |
|
|
|
|||
(gij ) = |
0 |
(x1 cos x3 )2 |
0 |
. |
|
|
|
(x1 )2 |
|
|
0 |
0 |
|
|
|
|
|
|
|
Это симметричная матрица с нулевыми недиагональными элементами, что характерно для ортогональных систем координат.
Вычисляя по указанным правилам компоненты сопряженной метрической матрицы, получим:
|
1 |
0 |
0 |
|
|
|
|||
(gij ) = |
0 |
(x1 cos x3 )−2 |
0 |
. |
|
|
|
(x1 )−2 |
|
|
0 |
0 |
|
|
|
|
|
|
|
|
Задача 1.5. Найти разложение базисных векторов Э j по базисным векто- |
||||||||||||||
рам Эi |
в точке M в случае введенной сферической системы координат. |
|
|||||||||||||
|
Решение. |
Э2 = g 2i Эi = (x1 cos x3 )−2 |
|
|
|
|
= (x1 )−2 |
|
|
||||||
|
|
Э1 = g1i Эi = Э1, |
Э2 , Э3 = g3i Эi |
Э3. |
|
||||||||||
|
Дополнительные задачи |
|
|
|
|
|
|
|
|
|
|
||||
|
Задача 1.6. Упростить выражения δ 2ni , |
δ i A |
δ j , |
δ i |
δ j , |
δ i |
δ jδ k , |
δ i |
δ j Ak , |
||||||
|
|
|
|
|
|
i |
|
2 |
ji 1 |
j |
k |
j |
k i |
j |
k i |
δ i |
Ak , |
B xi x j |
, если B |
= −B |
ji |
. |
|
|
|
|
|
|
|
|
|
j |
i |
ij |
ij |
|
|
|
|
|
|
|
|
|
|
|
|
Задача 1.7. Показать, что (Pijk + Pjki + Pjik ) xi x j xk = 3 Pijk xi x j xk .
Задача 1.8. Для заданных матриц
8
|
2 |
0 |
3 |
|
, (xi ) = (2,1, 4) , ( yi ) = (3, 7, -1) |
(aij ) = |
5 |
1 |
2 |
|
|
|
4 |
5 |
7 |
|
|
|
|
|
вычислить |
|
а) |
a x j , |
б) a xi , в) |
a xi y j , г) |
a yi x j , |
д) a |
δ j , |
||||
|
|
|
|
|
|
|
ij |
ij |
ij |
ij |
ij |
i |
е) |
a − |
2 |
δ l |
a |
xi y j . |
|
|
|
|
|
||
|
|
|
|
|
|
|||||||
|
ij |
5 |
|
j |
ll |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Задача 1.9. Решить задачи 1.2-1.5 в случае цилиндрической системы коор- |
|||||||||||
динат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 1.10. Сколько |
различных |
соотношений |
содержит |
выражение |
|||||||
gij |
= Эi |
× Эj ? |
|
|
|
|
|
|
|
|||
Задача 1.11. Доказать, что gij = Эi × Э j .
Задача 1.12. Доказать, что Эi × Эj = δ ij .
Задача 1.13. Доказать, что Эi = gij Э j .
Задача 1.14. Определить компоненты метрической матрицы для косоугольной системы координат, первая ось которой параллельна оси абсцисс декартовой системы координат, а вторая ось образовывает с первой угол α .
Задача 1.15. Найти вектора сопряженного базиса, если
|
|
|
|
+ 8 k . |
Э1 = 3i |
+ 8 k , Э2 = i |
+ 2 k , Э3 = 2 i |
+ 5 j |
Задача 1.16. Указать, какая из систем координат с метрической матрицей
g11 |
0 |
0 |
|
|
1 |
cosθ12 |
cosθ13 |
|
|
1 |
0 |
0 |
|
|||||
а) |
0 |
g |
22 |
0 |
, |
б) cosθ |
1 |
|
cosθ |
23 |
|
, в) 0 |
1 |
0 |
||||
|
0 |
|
|
|
|
|
12 |
cosθ |
|
1 |
|
|
0 |
0 |
1 |
|
||
0 |
g |
33 |
cosθ |
23 |
|
|||||||||||||
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
||
является 1) ортонормированной, 2) нормированной неортогональной, 3) ортогональной ненормированной.
Задача 1.17. В некоторых случаях, например при изучении течения в тонком слое вблизи тела, удобно использовать специальную криволинейную систему координат. Если течение рассматривается как плоское, система координат вводится в плоскости следующим образом. Пусть в плоскости течения
граница тела |
– |
гладкая |
кривая |
L , заданная параметрически |
|
|
|
длина дуги кривой L . Тогда в окрестности |
|
r = f (s) = a (s)i |
+ b (s) j , где s – |
|||
кривой каждой точке с радиус-вектором r |
с помощью рассматриваемой сис- |
|||
9
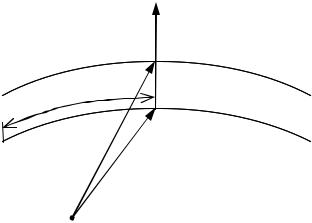
темы координат можно поставить в |
|
|
|
n |
|||
соответствие пару чисел ( s, h) , опре- |
|
|
|
||||
|
|
|
|
||||
деляемых из уравнения (рис. 2) |
|
|
|
|
|||
|
r = f ( s) + n ( s) h , |
|
|
|
r h |
||
|
|
|
s |
||||
где n (s) – |
единичная нормаль к кри- |
|
|
L |
|||
|
|
|
|||||
|
|
|
|
||||
вой L , h – |
расстояние до L . |
O1 |
|
|
f (s) |
||
Найдите базис системы коорди- |
|
|
|
|
|||
нат x1 = s , |
x2 = h |
и |
ковариантные, |
|
|
|
|
контравариантные |
и |
смешанные |
|
O |
Рис. 2 |
||
компоненты ее метрического тензо- |
|
|
|
||||
|
|
|
|
||||
ра.
10
ЗАНЯТИЕ 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. ИНВАРИАНТНЫЕ ОБЪЕКТЫ
Основные формулы и определения
Преобразование координат характеризуется соотношениями
x |
i |
= x |
i |
1 |
2 |
3 |
= x |
i |
(x |
j |
|
|
(x ' ,x ' |
,x ') |
|
') и выражает отображение областей изменения пе- |
|||||
ременных xi |
и x 'j |
друг на друга. Штрих в дальнейшем означает переменную |
||||||||
в новой системе координат. Отображение является непрерывным, взаимно однозначным, если якобиан преобразования 
 ¶xi
¶xi 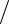 ¶x 'j
¶x 'j 
 ¹ 0,¥ ; при этом якоби-
¹ 0,¥ ; при этом якоби-
ан обратного преобразования 
 ¶x 'i
¶x 'i 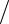 ¶x j
¶x j 
 ¹ ¥ , 0.
¹ ¥ , 0.
При переходе от одной системы координат к другой используются фор-
мулы преобразования:
|
|
i |
|
|
¶xi |
1 |
|
|
|
¶xi |
2 |
¶xi |
3 |
|
¶xi |
j |
|||||
дифференциала: |
dx |
|
= |
|
|
dx ' |
+ |
|
|
dx ' + |
|
|
dx ' = |
|
|
dx ', |
|||||
|
|
1 |
2 |
3 |
|
j |
|||||||||||||||
|
|
|
|
|
¶x ' |
|
|
|
|
|
¶x ' |
|
¶x ' |
|
|
¶x ' |
|
||||
базисных векторов: |
Э = |
¶r |
= |
|
¶r |
|
|
¶x 'j |
= ¶x 'j |
Э¢ , |
Э j = |
¶x j |
Э'm , |
||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
i |
|
|
¶xi |
|
|
¶x 'j ¶xi |
¶xi |
j |
|
|
¶x 'm |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
компонент метрической матрицы:
|
|
|
|
α |
β |
× Э¢ |
α |
β |
|
|
|
g |
ij |
= Э × Э |
j |
= ¶x ' |
¶x ' |
Э¢ |
= ¶x ' ¶x ' g ' |
, |
|||
|
i |
¶xi |
¶x j |
α |
β |
¶xi |
¶x j |
αβ |
|
||
|
|
|
|
|
|
|
|
||||
компонент вектора:
компонент тензора второго ранга:
g |
ij |
= |
¶xi |
|
¶x j |
|||||
|
α |
|
|
|
β |
|
|
|||
|
|
|
¶x ' |
|
¶x ' |
|||||
|
|
|
ai |
= |
|
¶xi |
|
|||
|
|
|
¶x¢ j |
|||||||
|
|
|
|
|
|
|
||||
|
T |
= |
¶x¢i |
|
¶x¢ j |
|||||
|
|
|
|
|
|
|||||
|
|
αβ |
|
¶xα |
|
¶xβ |
||||
|
|
|
|
|
||||||
Инвариантными относительно преобразования координат называют свойства, не меняющиеся при названном преобразовании. В частности, инвариантным является квадрат расстояния между близкими точками (форма записи остается неизменной):
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
β |
|
|
¶x |
i |
|
γ |
¶x |
j |
|
|
ν |
|||
|
2 |
|
|
|
|
i |
|
|
|
j |
|
¶x ' |
|
¶x ' |
|
|
|
|
|
|
|
|||||||
ds |
|
= g |
|
dx |
dx |
|
= |
|
|
|
|
|
g ' |
|
|
|
dx ' |
|
|
|
dx ' = |
|||||||
|
ij |
|
|
i |
|
|
j |
|
|
γ |
|
|
ν |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
¶x |
|
¶x |
αβ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
α |
|
|
β |
|
|
|
|
γ |
ν |
|
|
¶x ' |
α |
|
¶x ' |
|
2 |
|
|||||
|
|
= δ |
δ |
|
|
|
|
|
|
|
|
|
|
'dx |
β |
'= ds |
. |
|||||||||||
|
|
γ |
|
g ' dx ' dx ' = g ' dx |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
ν |
|
|
αβ |
|
|
|
|
|
|
αβ |
|
|
|
|
|
|
|
|
|
|||
Вектор a – линейная комбинация базисных векторов, инвариантная относительно непрерывного, однозначного преобразования координат:
a = ai Э = |
¶xi |
a¢ j ¶x¢γ |
Э¢ = δ γ a¢ j Э¢ = a¢ j Э¢ . |
|||
|
||||||
i |
¶x¢ j |
¶xi |
γ |
j |
γ |
j |
|
|
|
|
|
||
Вектор может быть записан в ко- и контравариантных компонентах:
11
