
Поташев
.pdf
|
|
1 |
|
2 |
2 |
|
1 |
3 |
1 |
2 |
1 |
|
3 |
||
I1 = SpT , I2 |
= |
|
SpT |
- SpT , I3 |
= |
|
Sp T - |
|
Sp T ×Sp T + |
|
SpT . |
||||
2 |
3 |
2 |
6 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4.10. Показать, что след антисимметричной части тензора второго ранга равен нулю.
Задача 4.11. Найти главные значения и главные направления тензора T ,
|
7 |
3 |
0 |
|
если в декартовой системе координат (Tiiki ) = |
3 |
7 |
4 |
. |
|
0 |
4 |
7 |
|
|
|
Задача 4.12. В ортогональной декартовой системе координат найти главные значения и главные направления симметричной части тензора с компо-
|
|
a 2a |
2a |
||||
|
ij |
|
|
|
|
|
|
нентами (T |
) = |
0 |
a |
2a |
. |
||
|
|||||||
|
|
|
0 |
0 |
a |
|
|
Задача 4.13. Непосредственным вычислением найти инварианты тензора с
|
6 |
-3 |
0 |
|
. Ответ: I1 = 20, I2 = 123, I3 = 216 . |
компонентами (Tij ) = |
-3 |
6 |
0 |
|
|
|
0 |
0 |
8 |
|
|
|
|
|
22

ЗАНЯТИЕ 5. ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА И ТЕНЗОРА ПО КООРДИНАТЕ
Основные формулы и определения
Коэффициенты связности (символы Кристоффеля первого рода) Γαk i
вводятся при дифференцировании базисных векторов:
¶ Э |
k |
|
¶ Эα |
α |
|
k |
α |
Эk , |
|
Э |
|||
¶ xi |
= Gα i |
¶ xi |
= -Gk i |
|
||
|
|
|
|
|
и могут быть вычислены по формулам
|
|
1 |
|
¶ gi s |
|
¶ gk s |
|
¶ gk i |
|
||
Gil k |
= |
|
gl s |
|
+ |
|
- |
|
. |
(5.1) |
|
2 |
¶ xk |
¶ xi |
¶ xs |
||||||||
|
|
|
|
|
|
|
|||||
Дифференцирование вектора по координате:
– ковариантная производная от контравариантных компонент:
|
|
|
α |
|
¶ w |
|
|||
º (Ñi |
wα )Эα = |
¶ w |
+ wβ Gαβ i Эα , |
|
|
¶ xi |
|||
¶ xi |
|
|
||
– ковариантная производная от ковариантных компонент:
|
|
|
|
|
¶ wα - w |
|
¶ w |
º (Ñ w |
) Эα = |
||||
|
|
|||||
¶ xi |
i |
α |
|
¶ xi |
β |
|
|
|
|
|
|
||
Дифференцирование тензора по координате:
Gαβ i Эα .
|
|
|
|
α β |
|
|
|
¶T |
|
¶T |
|
||||
º (Ñi |
T α β )Эα Эβ = |
|
+ T k β Gαk i |
+ T α k Gkβi Эα Эβ . |
|||
¶ xi |
¶ xi |
||||||
|
|
|
|
||||
Символический вектор-оператор Гамильтона «набла»: Ñ = Ñi Эi .
Градиент скалярной функции: |
|
|
|
∂ψ |
|
|
|
|
|
|
|
||
gradψ = Ñψ (xi ) = Ñi Эi ψ = Ñi ψ Эi = |
Эi . |
|||||
¶ xi |
||||||
|
|
|
|
|
||
Производная функции по направлению n : |
|
|
||||
∂ψ |
|
n |
|
|
||
|
= Ñψ × |
|
. |
|
(5.2) |
|
¶ n |
|
n |
|
|
|
|
Примеры решения задач
Задача 5.1. Вычислить коэффициенты связности в сферической и цилиндрической системах координат.
Решение. С использованием соотношения (5.1) получим, что в сферической системе координат отличны от нуля лишь компоненты
23

G122 = -x1 cos2 x3 , |
G133 = -x1, |
G122 = G212 =1 x1 , |
|||
G232 = G322 = - tg x3 , |
G133 = G313 |
= 1 x1 , G322 |
= |
1 |
sin (2 x3 ), |
|
|||||
|
|
|
2 |
|
|
в цилиндрической системе координат отличны от нуля лишь следующие компоненты
|
|
|
Γ2 = Γ2 |
= 1 r , Γ1 |
= −r . |
|
|||||||
|
|
|
21 |
12 |
|
|
|
22 |
|
|
|
|
|
|
Задача 5.2. Определить производную |
|
тензора первого ранга (вектора) |
||||||||||
= a |
i |
|
|
1 |
|
2 |
, x |
3 |
, считая, |
что он задан в цилин- |
|||
a |
|
Э по каждой из трех координат x , x |
|
|
|||||||||
|
|
|
i |
(x1 = r, x2 = ϕ, x3 = z ) |
|
||||||||
дрической системе координат |
следующим образом: |
||||||||||||
a1 = 2 r 2 + 3 z , a2 = 0 , a3 = 5 r + 2 z2 . |
|
|
|
|
|
|
|
|
|
||||
|
Решение. Производной тензора первого ранга по координате является |
||||||||||||
|
|
|
|
∂ a |
|
= (Ñ j |
ai )Эi = bi Эi , |
|
|||||
также тензор первого ранга b = |
|
компоненты которого |
|||||||||||
¶ x j |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– ковариантные производные компонент исходного тензора:
|
|
|
|
|
|
|
bi = Ñ j ai = |
|
|
¶ ai |
|
+ ak Gik j . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
¶ x j |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда компоненты результирующего вектора запишутся так |
||||||||||||||||||||||||||||||
|
|
1 |
|
¶ a1 |
|
1 1 |
|
2 1 |
|
|
3 1 |
|
|
¶ a1 |
|
|
|
|
||||||||||||
|
|
b |
|
= |
|
|
+ a G |
|
+ a |
|
|
|
G |
2 j |
+ a |
|
|
G |
3 j |
= |
|
|
, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
¶ x j |
|
1 j |
|
|
|
|
|
|
|
|
|
|
|
¶ x j |
|
|
|
|
|||||||
|
|
|
|
= |
+ a G |
|
+ a |
|
|
G |
|
|
+ a |
|
G |
|
|
|
|
|
|
|
||||||||
|
|
b |
2 |
¶ a2 |
2 |
2 |
2 |
|
3 |
2 |
= a G |
2 |
, |
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
¶ x j |
|
|
1 j |
|
|
|
|
|
|
2 j |
|
|
|
|
|
3 j |
|
|
1 j |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
b |
3 |
= |
¶ a3 |
|
1 |
3 |
+ a |
2 |
G |
3 |
|
+ a |
3 |
G |
3 |
= |
|
¶ a3 |
. |
|
|
|
||||||
|
|
|
|
|
+ a G |
|
|
|
|
2 j |
|
3 j |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
¶ x j |
|
1 j |
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ x j |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В частности, при j = 1 получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
b1 = ¶ a1 = |
¶ (2 r 2 + 3 z ) |
= 4 r, b2 = a1 G2 = 0, b3 = |
¶ a3 |
= |
|
¶ (5 r + 2 z2 ) |
= 5 |
|||||||||||||||||||||||
|
¶ x j |
|
||||||||||||||||||||||||||||
¶ x1 |
¶ r |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
¶ r |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и результирующий тензор первого ранга принимает вид b = 4 r Э1 + 5 Э3 . |
||||||||||||||||||||||||||||||
Аналогично, |
при |
j = 2 |
получим |
b = (2 r + 3 z r )Э2 . При j = 3 – |
||||||||||||||||||||||||||
b = 3Э1 + 4 z Э3 .
Задача 5.3. Напряженное состояние в любой точке сплошной среды задано тензором
24

|
|
3 x y |
5 y2 |
0 |
|
|
Σ = |
|
|
2 |
|
|
|
|
5 y |
|
0 |
2 z . |
||
|
|
0 |
|
2 z |
0 |
|
|
|
|
|
|
|
|
Определить вектор напряжения в точке P (2;1; 
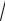 3 ) на площадке, касательной
3 ) на площадке, касательной
в этой точке к цилиндрической поверхности y2 + z2 = 4.
Решение. Компоненты напряжения в точке P принимают значения
|
6 |
|
5 |
|
0 |
|
|
|
Σ = |
|
|
|
|
|
|
|
. |
5 |
|
0 |
|
2 |
3 |
|||
|
|
|
|
|
|
|
|
|
0 |
2 |
3 |
0 |
|
|
|||
|
|
|
|
|||||
Единичный вектор нормали в точке P определяется вектором
gradϕ = Ñ( y2 + z2 - 4) = 2 y j + 2 z k .
Следовательно, в точке P : Ñϕ = 2 j + 2 
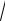 3 k .
3 k .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда единичный вектор нормали в точке |
P есть |
+ 3 k 2 . Век- |
|||||||||||||||||||||
n |
= j 2 |
||||||||||||||||||||||
тор напряжения на площадке, перпендикулярной к n в точке P , равен |
|||||||||||||||||||||||
6 |
5 |
|
0 |
|
|
|
0 |
|
|
|
5 / 2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
. |
|
|
|
|
|
||
5 |
0 |
|
2 3 |
1/ 2 |
3 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 2 3 |
0 |
|
|
|
|
3 2 |
|
|
|
3 |
|
|
|
|
|
|||||||
Дополнительные задачи
Задача 5.4. Вывести формулу ковариантного дифференцирования ковариантных по обоим индексам компонент тензора второго ранга.
Задача 5.5. Вывести формулу ковариантного дифференцирования тензора
третьего ранга T = T××αγ β ×Эα Эβ Эγ .
Задача 5.6. Исходя из определения базисных векторов, доказать, что
Gαi j = Gαj i .
Задача 5.7. В цилиндрической системе координат найти ковариантные производные от ковариантных компонент вектора W :
W1 = 3 x1 sin x2 , W2 = (x1 )2 cos x3 , W3 = (x3 )2 ln x1 .
Задача 5.8. Вычислить ковариантные производные от компонент вектора в сферической системе координат:
w1 = 2 x1 cos x3 , w2 = ln x1, w3 = tg x2 .
25

Задача 5.9. Доказать равенства:
а) Ñi (wα + vα ) = Ñi wα + Ñi vα , б) Ñi (wα vβ ) = (Ñi wα )vβ + wα Ñi vβ .
Задача 5.10. В цилиндрической системе координат найти ковариантные производные от ковариантных компонент тензора:
|
1 |
3 |
0 |
|
1 |
tg x |
2 |
|
|
x ln x |
|
x |
|
|
|
||||
(Tij ) = |
0 |
|
x3 ctg x2 |
|
) |
0 |
|
|
. |
|
1 |
2 |
0 |
1 |
2 |
|
2 |
|
|
x tg x |
|
(x |
sin x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
Задача 5.11. Найти производную функции λ = x2 + 2 x y - z2 по направлению, заданному единичным вектором n = (2 7; -3
7; -3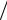 7; -6
7; -6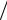 7).
7).
Задача 5.12. Задано скалярное поле температуры T = T ( x, y, z ) = x y - 5 z . В точке пространства ( x = 2, y = 3, z = 0) определить максимально и минимально возможные значения ее производной по направлению.
Задача 5.13. В точке пространства с координатами |
x = y = z = 0 заданы |
||
значение давления |
|
|
+ 4 k . Определи- |
p = 1 и градиент давления grad p =1i |
+ 3 j |
||
те приближенно значение давления в точке, расположенной в малой окрестности данной точки и имеющей координаты x = 0.01, y = 0.02 , z = −0.01.
|
Задача 5.14. Найти выражение ковариантной производной от компоненты |
||||
T |
α × тензора 2-го ранга со смешанным строением индексов. |
||||
×β |
|
|
|
|
|
|
Задача 5.15. Напряженное состояние в любой точке сплошной среды за- |
||||
дано тензором |
|
|
|
|
|
|
|
3 x2 |
4 x y −5 z |
||
|
Σ = |
4 x y |
0 |
0 |
. |
|
|
−5 z |
0 |
0 |
|
|
|
|
|
|
|
Определить вектор напряжения в точке P (
 2; 2;1) на площадке, касательной в этой точке к цилиндрической поверхности y2 + 2 x2 = 8 .
2; 2;1) на площадке, касательной в этой точке к цилиндрической поверхности y2 + 2 x2 = 8 .
26
ЗАНЯТИЕ 6. ОСНОВНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ
Основные формулы и определения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Градиент (тензорное произведение набла): |
|
|
grad ( |
) = Ñ ( |
) , |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gradψ (xi ) |
= |
∂ψ |
|
|
Эi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.1) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ xi |
|
|
|
|
|
|
|
div ( |
) = Ñ ×( |
) , |
|
||||||||||||||||||||||||||||||
Дивергенция (скалярное произведение набла): |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶ (aα |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
= Ñi |
|
|
i |
= |
|
¶ ai |
+ a |
k |
|
|
i |
|
= |
1 |
|
|
|
g |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
div a |
|
a |
|
|
|
|
|
|
Гk i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
(6.2) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
¶ xi |
|
|
|
|
|
|
|
|
|
|
¶ xα |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Ротор (векторное произведение набла): |
|
|
|
|
|
|
|
|
rot ( |
) = Ñ´( |
). |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
(rotV )k |
|
= ε k i |
j Ñi V j |
= |
|
|
|
(Ñi V j - Ñ j Vi ), |
|
|
|
|
|
|
|
|
(6.3) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где i, j, k |
образуют циклическую перестановку (1,2,3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
D( |
|
) = div (grad ( |
)) |
|
|
|
|
|
|
|
|
|
)). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Лапласиан: |
|
|
|
|
|
|
|
|
= Ñ ×(Ñ ( |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
1 ¶ |
|
|
|
|
|
|
|
|
|
|
|
|
¶ψ |
|
|
|
¶ |
|
|
|
|
|
¶ψ |
|
|
¶ |
|
|
|
|
¶ψ |
|
|
|||||||||||||||||||||||||||||
Dψ = |
|
g |
|
|
|
|
g |
+ |
|
|
|
g g |
+ |
|
g |
|
g |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
33 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
22 |
|
|
|
|
|||||||||||||||
|
|
g |
|
¶x1 |
|
|
|
|
g11 |
|
|
|
¶x1 |
|
¶x2 |
|
|
|
|
|
g22 |
¶x2 |
|
|
¶x3 |
|
|
|
g33 |
|
|
¶x3 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Псевдотензор Леви-Чевиты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
, если (i, j, k )-четная перестановка, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε i j k = |
|
|
|
|
|
|
g , если (i, j, k )- нечетная перестановка, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0, если индексы повторяются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, если (i, j, k ) -четная перестановка, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εi j k |
|
|
|
|
|
g , если (i, j, k )- нечетная перестановка, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
= - |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0, если индексы повторяются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторное поле a (xi ) |
|
называется потенциальным, если существует та- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
кое скалярное поле ϕ (xi ), что a = grad ϕ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Векторное поле a (xi ) |
называется безвихревым, если всюду rot a = 0 . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Векторное поле является соленоидальным, если его поток через любую поверхность равен нулю, что равносильно условию div a = 0 .
27
Примеры решения задач Задача 6.1. Записать градиент скалярной функции в декартовой и сфери-
ческой системе координат. |
|
|
|
|
|
Решение. Для декартовой системы координат: |
|
|
|||
gradψ ( x, y, z ) |
= ∂ψ i + |
∂ψ j + |
∂ψ k . |
||
|
∂ x |
|
∂ y |
∂ z |
|
Для сферической системы координат: |
|
|
|
|
|
gradψ (r,ϕ, λ ) = |
∂ψ |
|
∂ψ |
∂ψ |
|
∂ r Э1 |
+ |
∂ϕ Э2 + ∂ λ |
Э3 . |
||
Задача 6.2. Записать дивергенцию вектора в декартовой и сферической системе координат.
Решение. Согласно (6.2) для декартовой системы координат:
|
( x, y, z ) = |
∂ a |
x |
+ |
∂ ay |
+ |
∂ a |
z . |
div a |
|
|
|
|||||
∂ x |
∂ y |
|
||||||
|
|
|
|
∂ z |
||||
Для сферической системы координат:
div a (r,ϕ, λ ) = |
∂ a1 |
+ |
∂ a2 |
+ |
∂ a3 |
+ |
1 |
(a1 2 r cos λ − a3 r2 sin λ ) = |
|||||
∂ r |
∂ϕ |
∂ λ |
r 2 cos λ |
||||||||||
|
|
|
|
|
|
|
|
||||||
= |
∂ a1 + |
∂ a2 |
+ |
∂ a3 |
+ |
2 a1 |
− a3 tg λ |
|
|
||||
∂ϕ |
∂ λ |
|
|
|
|||||||||
|
∂ r |
|
|
r |
|
|
|
|
|
||||
Задача 6.3. Выразить дивергенцию вектора через его физические компоненты в сферической системе координат.
Решение. Используя результат задачи 6.2 и соотношение (3.2), получим
div a (r,ϕ, λ ) = |
∂ ar + |
1 ∂ aϕ |
+ |
1 |
∂ aλ + |
2 ar |
− |
aλ |
tg λ . |
||
|
|
|
|
|
|
||||||
r cos λ ∂ϕ |
|
r |
|
||||||||
|
∂ r |
|
r ∂ λ |
|
r |
||||||
Здесь физические компоненты векторов обозначены символами соответствующих координат вместо нумерации и подписи «физ».
Задача 6.4. Для заданного поля скоростей сплошной среды
v |
x |
= x2 , v |
y |
= −3 y, v |
z |
= 0 |
|
|
|
|
вычислить изменение содержания данного вещества за единицу времени в объеме
V = {x [1, 2]} { y [2, 4]} {z [3, 15]} .
Решение. Изменение содержания вещества сплошной среды за единицу времени в объеме V есть разность между втекшим и вытекшим через ограничивающую объем поверхность количеством данного вещества. Это изменение может быть вычислено с использованием формулы Остроградского-Гаусса:
28
−dM = ∫ vn dS = ∫ div v dV .
S V
В рамках заданных условий это уравнение запишется в виде:
z2 |
y2 x2 |
z2 |
y2 |
(x2 − 3x) |
|
|
z2 |
y2 |
(−2 + 2)dydz = 0 . |
−dM = ∫ ∫ ∫ |
(2x − 3)dxdydz = ∫ ∫ |
|
x2 dydz = ∫ ∫ |
||||||
z1 |
y1 x1 |
z1 |
y1 |
|
|
x1 |
z1 |
y1 |
|
|
|
|
|||||||
|
|
|
|
||||||
Таким образом, для заданного поля скоростей в любой части полосы, ограниченной плоскостями x = 1 и x = 2 , изменения количества вещества не происходит.
Дополнительные задачи
Задача 6.5. Записать лапласиан скалярной функции в декартовой и сферической системах координат.
Задача 6.6. Выразить ротор вектора через частные производные его компонент. Записать ротор вектора в декартовой системе координат.
Задача 6.7. Записать дивергенцию вектора через его физические компоненты в цилиндрической системе координат.
Задача 6.8. Записать физические компоненты градиента скалярной функции в сферической и в цилиндрической системах координат.
Задача 6.9. Записать лапласиан скалярной функции в цилиндрической системе координат.
Задача 6.10. Показать, что тензор с компонентами |
Bik = εijk a j антисим- |
||||||||
метричен. |
|
|
|
|
|
|
|
|
|
Задача 6.11. Найти физические компоненты векторов gradψ , rotV |
и вы- |
||||||||
числить divV , |
ψ в цилиндрической системе координат, если |
|
|||||||
|
ψ = r 2 + sinϕ, V = z tgϕ Э + 4 r |
2 z Э + r sinϕ Э . |
|
||||||
|
|
|
|
|
1 |
|
2 |
3 |
|
Задача 6.12. Найти физические компоненты векторов gradψ , rotV |
и вы- |
||||||||
числить divV , |
ψ в сферической системе координат, если |
|
|||||||
ψ = ln r + cos λ, V = r cos λ Э + sinϕ tg λ Э + r |
2 cosϕ Э . |
|
|||||||
|
|
|
|
|
1 |
|
2 |
3 |
|
Задача 6.13. Для заданного поля скоростей сплошной среды |
|
||||||||
|
v |
x |
= 0, v |
y |
= y2 , v |
z |
= 3z |
|
|
|
|
|
|
|
|
|
|||
вычислить изменение содержания данного вещества за единицу времени в объеме
V = {x [0, 4]} { y [1, 2]} {z [1, 10]} .
29
Задача 6.14. Мгновенное поле скоростей твердого тела можно записать в
|
|
|
+ |
Э1 |
Э2 |
Э3 |
|
виде |
v |
= a |
b1 |
b2 |
b3 |
, где векторы a и b не зависят от положения рассмат- |
|
|
|
|
|
x1 |
x2 |
x3 |
|
риваемой частицы. Показать, что ротор этих скоростей равен 2bi , а дивергенция равна нулю.
Задача 6.15. Найти выражение ротора вектора скорости v = v (r,ϕ ) для плоского течения в полярных координатах и записать условие несжимаемости div v = 0 .
Задача 6.16. Упростить выражения а) rot grad f , б) div rot A .
Задача 6.17. Доказать, что а) всякое потенциальное векторное поле является безвихревым, б) всякое безвихревое поле является потенциальным.
Задача 6.18. Векторное поле a |
|
в сферических координатах имеет компо- |
||||
ненты |
|
|
|
|
|
|
a1 = |
2 k cos x2 |
, |
a2 = |
k sin x |
2 |
, a3 = 0 . |
(x1 )3 |
(x1 )2 |
|
||||
Доказать, что это поле потенциально и соленоидально, и найти его потенциал. Задача 6.19. Найти решения уравнения Лапласа ϕ = 0 в сферических координатах, если функция ϕ зависит лишь от одной сферической координаты
x1 , x2 или x3 . Рассмотреть все три случая.
30
ЗАНЯТИЕ 7. ЛАГРАНЖЕВО И ЭЙЛЕРОВО ОПИСАНИЕ СПЛОШНОЙ СРЕДЫ.
МАТЕРИАЛЬНАЯ ПРОИЗВОДНАЯ ПО ВРЕМЕНИ
Основные формулы и определения
Лагранжева (материальная) система координат ξ i связана с деформи-
рующейся средой.
Эйлерова (лабораторная) система координат xi связана с наблюдате-
лем. Если какое-либо свойство сплошной среды описано с помощью переменных Лагранжа (Эйлера), то имеем соответственно лагранжево (эйлерово) описание. Лагранжевы координаты фиксированных материальных частиц остаются неизменными в течение всего процесса движения сплошной среды.
Материальная (полная, индивидуальная, субстанционная) производная
|
|
d [ |
] = lim |
[ |
](t + Dt ) -[ ](t ) = ¶[ |
] |
|
|
|
= |
¶ [ |
] + (V ×Ñ)[ ]. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
t →0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d t |
|
|
|
|
|
|
|
|
|
|
|
Dt |
|
|
|
¶ t |
|
|
ξ i =const |
|
|
¶t |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ξ i =const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Примененный к вектору скорости V , оператор материальной производной |
|||||||||||||||||||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
dV |
= ¶V |
+ (V |
×Ñ)V |
= |
¶V +V ×gradV = |
¶V +V iÑ V . |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
dt |
|
¶t |
|
|
|
|
|
|
|
¶t |
|
|
|
|
|
|
|
¶t |
|
|
i |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Контравариантные компоненты вектора ускорения a = |
dV |
|
равны |
||||||||||||||||||||||||||||||||||
dt |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
j |
|
¶V j |
|
i |
|
|
|
j |
|
|
¶V j |
|
i ¶V j |
i β |
j |
|
|
dV j |
|
|
k |
j |
dV i |
||||||||||||
a |
|
= |
|
|
+V |
ÑiV |
|
= |
|
|
|
+V |
|
+V V |
Гβ i |
= |
|
|
+V |
|
|
Gk i |
|
. |
|||||||||||||
|
|
¶t |
|
|
|
¶t |
|
¶xi |
|
dt |
|
|
dt |
||||||||||||||||||||||||
Примеры решения задач |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Задача 7.1. Дано |
|
|
описание |
движения |
|
сплошной среды |
(континуума) |
||||||||||||||||||||||||||||||
x1 = ξ1 et |
+ ξ 3 (et |
|
−1), |
x2 = ξ 3 (et |
− e−t ) + ξ 2 , |
x3 = ξ 3 . |
а) С какой точки зрения |
||||||||||||||||||||||||||||||
описано движение? б) Убедиться, что лагранжевы координаты точек сплошной среды совпадают со значениями эйлеровых координат в началаный момент времени. в) Выразить лагранжевы координаты через эйлеровы.
Решение. а) Лагранжево описание. б) При t = 0 x1 = ξ1, x2 = ξ 2 , x3 = ξ 3 . в)
ξ1 = x1 e−t − x3 (1− e−t ), ξ 2 = x2 − x3 (et − e−t ), ξ 3 = x3 .
Задача 7.2. Определить компоненты вектора скорости точки сплошной среды как функции а) лагранжевых, б) эйлеровых координат и времени. Движение сплошной среды задано соотношениями задачи 7.1.
31
