Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Поташев

.pdf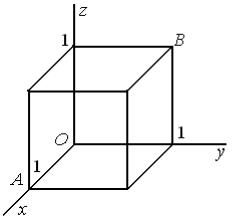

Скачиваний:

Добавлен:

10.02.2015

Размер:

466.82 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Решение.

V 1 =	∂ x1			= ξ1 et + ξ 3 et = (ξ1 + ξ 3 )et ,
а)	∂ t	ξ i =const
	∂ x2	ξ i =const		3 (et + e−t ), V 3 =	∂ x3

V 2 =			= ξ			= 0.
	∂ t		ξ i		∂ t	ξ i
			ξ i			ξ i

б) учитывая эйлерово описание движения, выразим ξ i через xi и t .В итоге имеем:

V 1 = x1 + x2 , V 2 = x3 (et + e−t ), V 3 = 0 .

Задача 7.3. Записать компоненты вектора a =

в сферической системе

координат.

Решение. Используя найденные ранее коэффициенты связности, полу-

чим:

a1 =

∂V 1

+ V 1

∂V 1

+ V 2

∂V 1

+ V 3 ∂V 1 − r cos2 λ (V 2 )2 − r (V 3 )2

∂t

∂r

∂ϕ

∂λ

a2 =

∂V 2 + V

1 ∂V 2 + V

2 ∂V 2

+ V 3 ∂V 2

2V 1V 2

−

2V 2V 3

∂ϕ

∂t

∂r

∂λ

tgλ

a3 =

∂V 3

+ V

1 ∂V 3

+ V

2 ∂V 3

+ V 3 ∂V 3

2V 1V 3

(V 2 )2 sin 2λ

∂t

∂r

∂ϕ

∂λ

Дополнительные задачи Задача 7.4. Какое из двух соотношений дает эйлерово описание преобра-

зования: 1) ξ i = ξ i (x j ,t ) 2) xi = xi (ξ j ,t ).

Задача 7.5. Описание движения сплошной среды, занимавшей первоначально куб с единичной стороной, дается выражениями задачи 7.1.

а) Какое движение совершает точка A (рис. 3)? в) Какое движение совершает точка B (рис. 3)? (Ответ: деформация чистого сдвига).

Задача 7.6. Дано поле скоростей в декартовой
системе координат V 1 =	x1	,	V 2 =	2 x2	,
						Рис. 3
1+ t			1+ t

V 3 =

3 x3

. Найти компоненты ускорения a =

d V

в эйлеровых и лагранжевых

d t

1+ t

переменных. Ответ:

2 x

6 x

{

= 0, a

= 2ξ

= 6ξ

+ t ) .

, a

(1 + t )2

(1+ t )2

}

Задача 7.7. Поле скоростей задано в переменных Лагранжа V 1 = −ξ 2 e−t , V 2 = −ξ 3 , V 3 = 2t . Найти компоненты ускорения в эйлеровой системе коор-

динат. Ответ: a1 = e−t (x2 + t x3 − t3 ), a2 = 0 ,							a3 = 2 .
Задача 7.8. Движение				континуума			задано	уравнениями:
x1 = A +	e− B λ	sin λ	( A + ω t ) ,	x2 = −B −		e− B λ	cos λ ( A + ω t ) ,	x3 = ξ 3 .	Дока-

	λ					λ

зать, что траектории всех частиц –					окружности, а величина скорости постоян-
на. Определить связь между				A и	B и лагранжевыми координатами ξ1, ξ 2 ,
совпадающими с x1 (0) , x2 (0) .
Задача 7.9. Дан			закон	движения			сплошной	среды	x = ξ1,

y = et (ξ2 + ξ3 )2 + e−t (ξ2 − ξ3 )2, z = et (ξ2 + ξ3 )2 − e−t (ξ2 − ξ3 )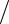2 . Определить компоненты скорости в эйлеровой и лагранжевой форме.

Задача 7.10. Задано поле перемещений в сопутствующей системе коорди-

нат u = (ξ1 − ξ 2 )2

Э1 + (ξ 2 + ξ 3 )2

Э2 − ξ1ξ 2 Э3 , являющейся в начальный мо-

мент времени декартовой прямоугольной. При ограничениях, принятых в теории малых деформаций, определите тензор деформаций и тензор поворота

в индивидуальной точке с лагранжевыми	координатами ξ1 = 0 , ξ 2 = 2 ,
ξ 3 = −1.
Задача 7.11. Вектор перемещения задан	в лагранжевых координатах

u1 = ξ1 (ea t −1), u2 = ξ 2 (eb t −1), u3 = ξ 3 (ec t −1). Найти вектор скорости v как

функцию эйлеровых координат xi .
Задача 7.12. Поле	скоростей	задано	вектором

v = (x1 )2 t Э1 + x2 t2 Э2 + x1 x3 Э3 . Определить скорость и ускорение частицы, находящейся в момент t = 1 в точке P (1,3, 2) .

ЗАНЯТИЕ 8. ПРИЛОЖЕНИЯ К МЕХАНИКЕ. ПЕРЕМЕЩЕНИЕ. ДЕФОРМАЦИЯ

Основные формулы и определения

Компоненты тензора деформаций могут быть выражены через компоненты вектора перемещений u j :

ε		=	1	(Ñ	u		+ Ñ u ).	(8.1)
	ij					j
		2		i			j i

Уравнения совместности в случае бесконечно малых деформаций:

¶2εij	+	¶2ε	km	-	¶2ε	ik	-	¶2ε jm	= 0 .	(8.2)
¶ xk ¶ xm		¶ xi ¶ x j			¶ x j ¶ xm			¶ xi ¶ xk

Тензор градиента скорости определяется матрицей, составленной из ча-

¶ vi

стных производных компонент вектора скорости сплошной среды .

¶ x j

Симметричная часть тензора градиента скорости представляет собой

тензор скоростей деформаций. Антисимметричная часть – тензор завихренности.

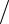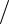Вихревой линией называется такая линия, касательная к которой в каждой точке движущейся среды направлена по вектору вихря q = Ñ ´ v . Уравнения вихревых линий имеют вид dx1q1 = dx2 q2 = dx3q3 .

Примеры решения задач Задача 8.1. Для некоторого момента времени задано векторное поле ско-

рости	течения		жидкости		в	декартовой	системе	координат
					+ 2 z k . Что можно сказать о характере движе-
v = vx i	+ vy j	+ vz k = x i		− 3 y z j	+ 2 z k . Что можно сказать о характере движе-

ния частицы среды, находящейся в данный момент времени в точке пространства с координатами x = 1, y = 2 , z = 3?

Решение. Поле скоростей позволяет определить поступательную, деформационную и вращательную составляющие движения любой частицы среды. Скорость движения данной частицы определяется подстановкой координат

частицы в векторное поле скорости: v = 2 i −18 j + 6 k .

Согласно физическому смыслу дивергенции вектора, для векторного поля скорости течения жидкости (при отсутствии в потоке внутренних источников массы) div v определяет относительную скорость изменения объема бесконечно малой индивидуальной частицы:

lim	Vɺ	= div v =	∂ x +	∂ (−3 y z )	+	∂ (2 z )	= −3 z + 3 .

V →0 V			∂ x	∂ y		∂ x

Для данной частицы div v = −6 < 0 , что говорит о проявлении в данный момент времени тенденции к сжатию частицы, уменьшению ее объема и увеличению плотности.

Согласно физическому смыслу ротора вектора, для векторного поля скорости течения жидкости rot v определяет мгновенную угловую скорость ω вращательного движения бесконечно малой индивидуальной частицы:

∂ (2 z )

∂ (−3 y z )

∂ (2 z )

∂ x

2ω = rot v

−

∂ z

∂ y

∂ x

∂ z

∂ (−3 y z )

∂ x

−

k = 3 y i .

∂ x

Для данной частицы 2ω = 6 i –

∂ y

ось вращения параллельна оси Ox , вращение

происходит против хода часовой стрелки по отношению к этой оси. Зависимость величин v, div v, rot v от координат говорит о том, что час-

тицы деформируемой среды в общем случае движутся с разными скоростями, испытывают различные деформации и вращательные движения.

Задача 8.2. Некоторое течение задано в декартовой системе координат по-

лем скоростей	1	= 0 ,	v	2		1	2	− (x	3	)	2		− B t	, v	3		(x	2	)	2
лем скоростей	v	= 0 ,	v		= A x x			− (x		)		e		, v		= A	(x		)

1	3	− B t	,	где
− x x	e		,	где

A, B – константы. Найти тензор градиента скорости и вычислить тензор скоростей деформации и тензор завихренности в точке P (1, 0, 3) в момент t = 0 .

Решение.

Тензор

градиента

скорости

равен

∂ vi

−2 x3

Ae− B t . Этот тензор можно вычислить в точке P в

∂ x j

−x

2 x

−x

момент t = 0 . Его симметричная и антисимметричная составные части являются тензорами скоростей деформации и завихренности, соответственно:

−1.5A

1.5A

A −6 A

−3A

−3A .

−3A

−1.5A −3A

− A

−1.5A 3A

− A

Задача 8.3. Доказать,

что

для

поля

скоростей

v = ( Ax3 − Bx2 )Э1 + (Bx1 − Cx3 )Э2 + (Cx2 − Ax1 )Э3

вихревые

линии являются

прямыми. Написать их уравнения. Доказать, что такое поле скоростей пред-

ставляет вращение абсолютно твердого тела, так как для него тензор скоростей деформаций равен нулю.

Решение.		По	определению	вектора	вихря
q = Ñ´ v = 2(C Э + A Э + B Э ) . Тогда уравнения				вихревых линий	будут
	1	2	3
A dx3 = B dx2 ,	B dx1 = C dx3 ,		C dx2 = A dx1 . Интегрируя их, найдем уравнения

вихревых линий в конечной форме x3 = B x2 / A + K1 , x2 = A x1 / C + K3 , где Ki – постоянные интегрирования.

¶ vi

Вычислим матрицу тензора градиента скорости:

¶ x j

x1 = C x3 / B + K2 ,

	0	-B	A
=	B	0	-C .
	-A	C
	-A	C	0

Поскольку этот тензор антисимметричен в любой точке сплошной среды, то его симметричная составляющая (тензор скоростей деформаций) представляет собой нулевой тензор также во всех точках сплошной среды.

Задача 8.4. Считая деформации малыми, записать выражения для геометрических компонент тензора деформаций в декартовой, цилиндрической и сферической системах координат.

Решение: а) декартова с.к.:

ε xx

¶ u x , ε yy = ¶u y , ε zz =

¶ u z ,

¶ x

¶ y

¶ z

¶ u x

¶ u y

¶ u x

¶ u z

¶u y

¶ u z

¶ z

¶ x

¶ z

¶ y

¶ x

б) цилиндрическая с.к.

ε rr =

¶ ur

, ε ϕϕ =

¶uϕ

+ r ur , ε rϕ

¶ ur

¶uϕ

2uϕ

¶ r

¶ϕ

¶ r

¶u z

ε zz =

¶u z

, ε ϕ z =

¶ uϕ

ε rz =

¶ur

¶ u z

¶ z

¶ r

¶ z

¶ϕ

¶ z

в) сферическая с.к.

ε rr

¶ ur

, ε ϕϕ = ¶uϕ

+ uλ sin λ cos λ + r ur sin2 λ,

¶ r

¶ϕ

ε rϕ

¶ur

¶ uϕ

2uϕ

λλ =

¶ uλ

+ r ur ,

¶ϕ

¶ λ

¶ r

ϕλ

¶uϕ

¶ uλ

cos λ

, ε

rλ

¶ ur

¶uλ

¶ λ

sin λ

¶ λ

¶ r

¶ϕ

Задача 8.5. Деформированное состояние сплошной среды задано матри-

																														( x			)				( x				)				x			x
																															1				2					2			2			1			3
цей	тензора										деформаций														(εij ) = (x2 )2														x3						(x3 )2						.				Удовлетворяются ли
																														1		x		3			(x			3	)		2			5
																														x		x					(x				)					5

уравнения совместности?
Решение. Из 81 уравнения совместности только шесть различны:
	∂2ε11											∂2ε22									∂2ε12
	∂2ε11								+			∂2ε22						= 2			∂2ε12							,				∂						−		∂ ε						+		∂ ε						+		∂ ε				=			∂2ε
	(∂ x					)										)																∂								∂ ε				23				∂ ε			31					∂ ε		12					∂2ε			11
				2				2						1			2						1		∂ x		2																	23							31							12								11		,
				2				2						1			2						1				2				∂ x1									∂ x1								∂ x2								∂ x3							∂ x2 ∂ x3					,
												(∂ x								∂ x											∂ x1									∂ x1								∂ x2								∂ x3							∂ x2 ∂ x3
	∂2ε				22				+			∂2ε			33				= 2		∂2ε					23							∂						∂ ε			23			−		∂ ε			31			+		∂ ε		12		=			∂2ε			22
					22										33											23			,													23								31							12								22		,
	(∂ x3 )2											(∂ x2 )2																	,																																						,
	(∂ x3 )2											(∂ x2 )2									∂ x2 ∂ x3										∂ x2								∂ x1								∂ x2								∂ x3						∂ x3 ∂ x1
	∂	2	ε33									∂	2	ε11							∂	2		ε31									∂						∂ ε			23			+		∂ ε			31		−			∂ ε		12		=				∂2ε		11
									+									= 2										,														23								31							12								11		.
																															∂ x					3						1								2							3					1			2		.
	(∂ x1 )						2			(∂ x3 )							2			∂ x			3				1				∂ x								∂ x								∂ x								∂ x						∂ x			∂ x
	(∂ x1 )									(∂ x3 )										∂ x					∂ x

Непосредственной подстановкой в них заданных компонент матрицы деформаций можно удостовериться, что уравнения совместности выполняются.

Дополнительные задачи
Задача 8.6. Дано поле перемещений	u1 = 3 x1 (x2 )2	,

u3 = (x3 )2 − x1 x2 . Определить тензор деформаций εi j (x1, x2 , x3 ) удовлетворяются ли условия совместности.

3(x

)

+ x

−x

(

ij )

3 x x

/ 2

Ответ:

3 x1x2

+ x3

x1 / 2

, да.

−x

/ 2

2 x

x / 2

u2 = 2 x3 x1 ,

и проверить,

Задача 8.7. Некоторое течение задано полем скоростей в декартовой сис-

теме координат	1	= 0 ,	v	2		1	2	− (x	3	)	2		− B t	, v	3		(x	2	)	2	1	3	− B t	, где
теме координат	v	= 0 ,	v		= A x x			− (x		)		e		, v		= A	(x		)		− x x	e		, где

A, B – константы. Найти градиент скорости ∂ vi ∂ x j для этого движения и вычислить компоненты тензора скоростей деформации ei j и тензора скоро-

стей поворота wi j в точке P (1, 0,3) в момент времени t = 0 . Будет ли сплошная среда сжиматься при таком движении?

Задача 8.8. Дано

стационарное

поле

скоростей

)

+ x

Э2 . Найти скорости относительно точ-

= ( x )

− x

Э1

+ (x )

Q2 (1, 3

4 ,3), Q3 (1, 7

8 ,3), отнесенные к

ки P (1,1,3)

частиц в точках Q1 (1, 0,3) ,

расстоянию от этих точек до точки P . К чему стремятся отнесенные скорости

точек Qi

при стремлении последних к точке P ?

Задача 8.9. Что можно сказать об изменении объема и формы индивидуальной частицы сплошной среды, деформированное состояние которой характеризуется тензором с матрицей

	1	2	3
(εij ) =	2	4	−5	?
	3	−5	−5
	3	−5	−5

Задача 8.10. Однородное тело подвергается деформации сдвига так, что все плоскости, параллельные плоскости x1Ox2 , переходят в себя и все точки

тела перемещаются в направлении единичного вектора l = l1 e1 + l 2 e2 , параллельного этой плоскости. Найти тензор деформации тела.

Задача 8.11. Малая деформация тела задается тензором

	8	-1 -1
(εij ) =	1	6	0	×10−6 .
	-5	0	0
	-5	0	0

а) Определить тензор чистой деформации и тензор поворота.

б) Найти главные коэффициенты и главные направления деформации тела. в) Найти направление оси вращения и угол поворота тела.

ЗАНЯТИЕ 9. ПРИЛОЖЕНИЯ К МЕХАНИКЕ. НАПРЯЖЕНИЯ. УРАВНЕНИЯ РАВНОВЕСИЯ

Основные формулы и определения


σij – компоненты тензора напряжений S сплошной среды.
Вектор полного напряжения σ					на площадке с единичной нормалью n
вычисляется по формуле
σ			Эi Э j	× nk Э = σ			n j Эi = σ		Эi .
σ	= S ×n = σ	ij	Эi Э j	× nk Э = σ		ij	n j Эi = σ	n i	Эi .	(9.1)
		ij			k	ij		n i
Нормальное σ n	и касательное τ				напряжения в любой точке сплошной

среды на площадке с единичной нормалью n определяются тензором напряжений в этой точке и ориентацией площадки:

σ	n	= σ ×n = σ	n i	Эi	× nk Э = σ		n i	ni ,		(9.2)
						k
									.
τ =		σ ×σ - (σ n )2		=		σ n i σ ni - (σ n )2				(9.3)

Главные площадки – площадки, на которых отсутствуют касательные напряжения. Направления по нормали к этим площадкам определяют главные направления тензора напряжений, а нормальные напряжения, действующие на этих площадках, называются главными напряжениями или главными значе-

ниями тензора напряжений. Главные оси и главные значения тензора напряжений определяются по аналогии с принципом нахождения главных осей и главных значений тензора.

Среднее напряжение выражается через первый инвариант:

σ = SI 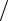3 = (σ1 +σ 2 +σ 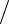3 )3 .

Интенсивность напряжений выражается через первый и второй инварианты тензора напряжений:

σi = 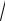2 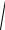3SII - S2I 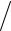2 .

Компоненты шарового тензора напряжений:

Sσ ij = σ gij

характеризуют лишь ту часть полных напряжений, которые вызваны изменением объема индивидуальных частиц и не связаны с их формоизменением.

Компоненты девиатора напряжения дополняют компоненты шарового тензора до полных напряжений:

Dσ ij = σ ij − σ gij

и характеризуют лишь ту часть полных напряжений, которые связаны лишь с изменением формы индивидуальных частиц и не связаны с изменением их объема.

Уравнения равновесия

∂σ ij	+ ρ b = 0 .	(9.4)
∂ x j	+ ρ b = 0 .	(9.4)
	i

Здесь ρ – плотность сплошной среды, bi – компоненты вектора распределенных массовых сил.

Примеры решения задач Задача 9.1. Напряженное состояние в некоторой точке задано тензором

aσ bσ

напряжений с матрицей

(σij ) = aσ

cσ . Определить константы a,b, c

bσ

cσ

так,

чтобы

вектор

напряжения

на

площадке с единичной нормалью

n =

Э +

в декартовой системе координат был равен нулю.

Решение. По уравнению (9.1) для данных тензора напряжений и вектора

нормали величина σ

= σ

n j должна быть равна нулю. Запишем это в мат-

ричной форме:

σ aσ bσ

a + b = −1,

aσ

cσ

, откуда a + c = −1,

bσ cσ σ

b + c = −1.

Решая эти уравнения, получим a = b = c = −1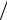2 . Тогда итоговая матрица тензора напряжений имеет вид:

	σ	−σ	2	−σ 2
(σij ) =	−σ 2	σ −σ 2			.
	−σ 2	−σ	2	σ
	−σ 2	−σ	2	σ

Задача 9.2. Напряженное состояние сплошной среды в декартовой прямо-

угольной системе координат задано полем тензора напряжений Σ с компо-

	2 x y	3 y2	0
нентами (σij ) =	3 y2	0	z	. Определите вектор полного напряжения, нор-
	0	z	1

мальное и касательное напряжения в точке P (2,1, 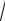3 ) на площадке, касатель-

ной к цилиндрической поверхности y2 + z2 = 4.

Решение. Компоненты напряжения в точке среды P принимают вид

	4	3	0
(σij ) =
(σij ) =	3	0	3	,

	0	3	1
	0	3	1

а единичный

вектор

нормали

точке

поверхности

grad Φ

F( x, y, z ) = y2 + z2 - 4 = 0 определяется вектором n=

grad F

= Ñ( y2

+ z2 - 4)

+ 2

(2 y j + 2 z k )

= 2 j

3 k ,

grad F

P = 4 , n=

j +

k .

В итоге вектор полного напряжения (9.1) определяется как

+ (σ 21 n1

σ = (σ11 n1 +σ12 n2 +σ13 n3 )i

+σ 22 n2 +σ 23 n3 ) j

+(σ 31 n1 +σ 32 n2 +σ 33 n3 )k

i +

+ 3 k ,

а нормальное (9.2) и касательное (9.3) напряжения будут равны:

σ n = σ n1 n1 +σ n 2 n2 +σ n 3 n3 =

×0 +

τ = σ n i σ ni - (σ n )2 = 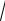39 .

Дополнительные задачи Задача 9.3. Тензор напряжений в точке сплошной среды задан матрицей

	7	0	-2	. Определите вектор полного напряжения σ n в данной точке
(σij ) =	0	5	0	. Определите вектор полного напряжения σ n в данной точке
	-2	0	4
	-2	0	4

на площадке, ориентация которой задается единичным вектором нормали

n = 2 Э1 - 2 Э2 + 1 Э3 . 3 3 3

Задача 9.4. Тензор напряжений в точке сплошной среды задан матрицей

	1	2	0
(σij ) =	2	3	5	. Определите нормальное напряжение в данной точке на пло-
	0	5	1
	0	5	1

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.09.2019634.88 Кб7Пособие_Веткиной_С.Н.l.doc
#
13.07.2019620.92 Кб15пособие_олимпCКОММЕНТАРИЯМИ.rtf
#
13.11.201993.49 Кб1Пособия за счет средств ФСС (Бератор 'Практичес...rtf
#
10.02.2015262.45 Кб5постановления кабМИНА.docx
#
03.05.2019105.98 Кб3постоянный ток.doc
#
10.02.2015466.82 Кб61Поташев.pdf
#
23.09.201964.61 Кб3Потребности.docx
#
23.09.201946.97 Кб9Потребность в познании, самопознании.docx
#
20.08.201962.73 Кб1почитайте, может поймете что нибудь).docx
#
13.08.2019241.66 Кб1Пояснительная записка. Линия метрополитена.doc
#
17.04.2019370.08 Кб5ПП р.docx