Поташев

a = ai Эi = a j Э j .

Здесь a j , ai – ко- и контравариантные компоненты вектора.

Тензор второго ранга – линейная комбинация диад базисных векторов, инвариантная относительно непрерывного, однозначного преобразования координат. Тензор второго ранга может быть записан в диадах векторов исходного и сопряженного базиса:

T = T αβ Эα Эβ = T×βi× Эi Эβ = Tα× ×j Эα Эj = Tαβ Эα Эβ .

Число индексов у компонент тензора T αβ определяет его ранг. Скаляр - тензор нулевого ранга, вектор – тензор первого ранга. Матрицей тензора называется матрица, составленная из его компонент.

Операция «жонглирования» индексами производится с использованием компонент метрической матрицы при переходе от ковариантных величин к контравариантным и наоборот. Например, для компонент вектора:

Диадой двух произвольных векторов a b является элемент девятимерного линейного пространства (тензор второго ранга), характеризуемый раз-

данного девятимерного пространства. Матрицей диады является матрица

щен. Скалярное же произведение впредь всегда будем обозначать точкой

( )×( ).

Метрический тензор в качестве компонент имеет элементы метрической матрицы.

12

Решение:

вектор в декартовой системе координат.

Решение. Для записи решения задачи необходимо отыскать компоненты вектора в декартовой системе координат.

Здесь при вычислении частных производных были использованы координаты точки приложения вектора. Таким образом, в декартовой системе координат:

Следует обратить внимание, что вектор a с теми же компонентами в сферической системе координат, но приложенный к другой точке пространства, имел бы иные компоненты в декартовой координатной системе.

Полученная матрица определяет компоненты тензора в базисе Эi Эk .

13

Задача 2.4. Доказать инвариантность и найти представления скалярного произведения векторов.

Задача 2.6. Записать матрицу диады, составленной из векторов a(1,0, 2) , b (0,3, −1) . В скобках указаны компоненты векторов в декартовой системе ко-

Дополнительные задачи

Задача 2.7. Показать, что компоненты тензора Кронекера δi j не изменяются при преобразованиях координат.

Задача 2.8. Найти связь между дифференциалами ковариантных компонент метрического тензора и дифференциалами его контравариантных ком-

понент. Ответ: dgij = −gim g jk dg mk .

Задача 2.9. Доказать, что если xi – декартовые координаты, а x 'j – произвольные криволинейные, связанные соотношением xi = xi (x 'j ), то компонен-

14

Задача 2.10. Задана прямолинейная, косоугольная система координат, угол между двумя координатными линиями в точке равен α , третья координатная линия перпендикулярна первым двум. Определить величины и на-

правления базисных векторов Эi и Эi .

Задача 2.11. Записать формулы преобразования сферической системы координат в цилиндрическую и найти якобиан преобразования.

Задача 2.12. Показать, что частные производные произвольной функции ϕ (x1, x2 , x3 ) преобразуются при переходе к новой системе координат как ковариантные величины.

Задача 2.13. Записать метрический тензор в сферической системе координат.

Задача 2.14. Получить формулы преобразования компонент Tαβ тензора при переходе от сферической системы к декартовой.

Задача 2.15. Составить матрицу из компонент следующего тензора второ-

Задача 2.16. Записать явный вид соотношений xi = xi (x′ j ) , если {xi } –

сферическая, а {x′i } – прямоугольная декартова СК. Найти якобиан преобра-

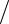зования ∂xi ∂x′ j . Для указанного перехода найти формулу преобразования

15

ЗАНЯТИЕ 3. ОПЕРАЦИИ НАД ТЕНЗОРАМИ. ФИЗИЧЕСКИЕ КОМПОНЕНТЫ ВЕКТОРА

Основные формулы и определения

Тензорное (внешнее) произведение тензоров есть тензор, ранг которого равен сумме рангов сомножителей, а компоненты произведению компонент сомножителей. В частном случае диада - тензорное произведение двух векто-

Сложение тензоров определяется только для тензоров одной валентности. Компоненты тензора суммы определяются как сумма компонент слагае-

Скалярное произведение тензоров вычисляется следующим образом:

Скалярное произведение тензоров – тензор, ранг которого меньше суммы рангов сомножителей на два.

Двойное скалярное произведение вычисляется следующим образом:

или при другом строении индексов:

Следом тензора называют двойное скалярное произведение тензора на метрический тензор:

Sp T = tr T = T : g .

Степенью n тензора называется последовательное n -кратное скалярное

n

произведение тензора самого на себя и обозначается T .

16

Физические компоненты вектора вводятся для ортогональных систем ко-

Дополнительные задачи Задача 3.3. В цилиндрической системе координат найти сумму тензоров:

Задача 3.4. Представить все формы записи тензора третьего ранга, используя тензорные произведения трех базисных векторов.

17

Задача 3.5. Найти выражение следа тензора второго ранга через его компоненты.

[T × D]× D .

Задача 3.7. Различаются ли матрицы, составленные из метрических коэффициентов смешанного типа, в декартовой, цилиндрической и сферической системах координат?

Задача 3.10. Пользуясь определением степени тензора, выразить компо-

ввести понятие физических компонент тензора второго ранга Tфизi j .

Задача 3.15. Доказать, что aфизi = aфиз i .

Задача 3.16. Записать выражение квадрата вектора в ортогональной системе координат через его физические компоненты.

18

ЗАНЯТИЕ 4. АЛЬТЕРНИРОВАНИЕ И СИММЕТРИРОВАНИЕ. ТЕНЗОРНАЯ ПОВЕРХНОСТЬ, ГЛАВНЫЕ ЗНАЧЕНИЯ

И ГЛАВНЫЕ НАПРАВЛЕНИЯ

Основные формулы и определения

Альтернирование и симметрирование тензора – выделение его антисим-

метричной и симметричной частей. Тензор называется симметричным (антисимметричным) по некоторой паре индексов, если компоненты его не меняются (изменяют только знак) при перестановке этих индексов местами. При выделении симметричной и антисимметричной частей тензоров второго ранга пользуются тождеством

Компоненты Sij , Aij представляют соответственно симметричную и антисим-

метричную части исходного тензора.

Тензорная поверхность симметричного тензора второго ранга в некоторой точке определяется уравнением:

Tij dxi dx j = C .

В осях, соответствующих главным направлениям, уравнение поверхности приводится к каноническому виду. Единичный вектор e , определяющий главное направление, удовлетворяет соотношению:

T -T g ×e = 0 ,

где T – величина соответствующего главного значения тензора.

Для нахождения главных значений и главных направлений тензора второго ранга необходимо выполнить следующую последовательность действий:

1.составить и решить относительно T характеристическое уравнение det (Tiiki -T δki ) = 0 ; в общем случае уравнение третьего порядка имеет

три решения, соответствующие трём главным значениям T(1) , T(2) , T(3) ,

2.для каждого найденного главного значения T(n) решить систему трёх уравнений (Tiiki -T δki )×e(kn) = 0 для отыскания трёх компонент соответст-

вующего главного направления e(n) = (e(1n) , e(2n) , e(3n) );

3.зная компоненты метрической матрицы пространства, нормировать найденные главные вектора.

19

Первый инвариант тензора второго ранга

I1 = T(1) + T(2) + T(3) .

Второй инвариант тензора второго ранга:

I2 = T(1) T(2) + T(2) T(3) + T(3) T(1) .

Третий инвариант тензора второго ранга:

I3 = T(1) T(2) T(3) .

Примеры решения задач

Задача 4.1. Установить, по каким парам индексов симметричен или антисимметричен тензор, если для его компонент выполняются равенства

αi j k l = αi k j l = −α j i k l = −αl j k i .

Решение. Из первого равенства можно заключить, что тензор симметричен по индексам (2, 3). Из второго (с учетом первого) – антисимметричен по (1, 2). Из последнего – антисимметричен по (1, 4). При решении подобных задач в сквозном равенстве необходимо сопоставлять выражения по принципу «каждый с каждым».

Задача 4.2. Определить матрицы компонент симметричной и антисимметричной частей тензора, если его компоненты заданы матрицей

1 2 3

(Tij ) = 4 7 8 .1 4 6

Решение. Используя тождество (4.1), получим

Задача 4.3. Найти главные значения и главные направления тензора T ,

Корни этого уравнения определяют три главных значения T(1) = 1, T(2) = 2 ,

T(3) = 4 .

20

довательно, для того, чтобы вектор главного направления не был нулевым,

Дополнительные задачи

Задача 4.4. Установить, по каким парам индексов симметричен или антисимметричен тензор, если для его компонент выполняются равенства