Metricheskie zadachi

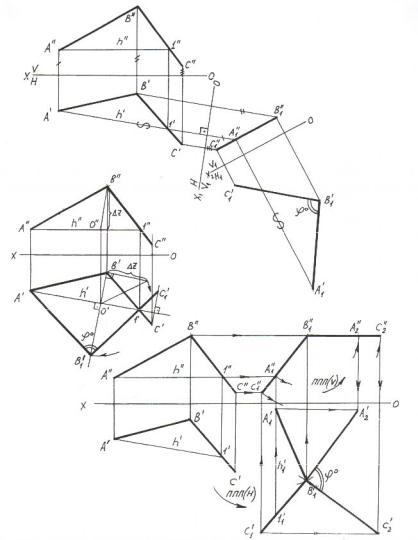
а)

б)

в)

Рисунок 5.4 – Определение плоского линейного угла между двумя прямыми:

а– переменной плоскостей проекций; б – вращением вокруг h;

в– плоско-параллельным перемещением

50

В первой задаче плоскость угла путём замены плоскостиV на V1 сначала переводится в проецирующее положение, а затем заменой Н на Н1 переводится в положение, параллельное плоскости Н1. На плоскость Н1 угол проецируется в натуральную величину.

Во второй задаче угол путём вращения вокруг горизонтали переводится в положение, параллельное плоскости Н. По окончании вращения угол проецируется на плоскость Н в натуральную величину.

В третьей задаче двумя плоско-параллельными перемещениями

ППП(Н) и ППП(V) переводится в положение, параллельное плоскости Н, и проецируется на неё в натуральную величину.

5.4 Определение угла между прямой и плоскостью

Определение угла между прямой и плоскостью является сложной геометрической задачей, которая может быть решена общегеометрическим методом и методом дополнительного угла.

Общегеометрический метод очень трудоёмок и включает в себя значительное количество построений. Предположим, требуется определить угол между прямой общего положенияАВ и плоскостью общего положения, заданной следами (рисунок 5.5,а). Задача решается в логической последовательности, исходящей из пространственного макета задачи (см. рисунок рядом с проекционным чертежом):

-строят точку встречи С прямой АВ с заданной плоскостью;

-опускают из точки В перпендикуляр на заданную плоскость;

-строят точку встречи перпендикуляра с плоскостью (точка D);

-соединяют точки С и D, определяют натуральную величину искомого угла ВСД путём построения натуральной величины треугольника ВСD на свободном поле чертежа. Перед этим предварительно определяют НВ сторон треугольника методом прямоугольного треугольника. Указанный способ редко используется в практике конструкторской работы.

51

а)

б)

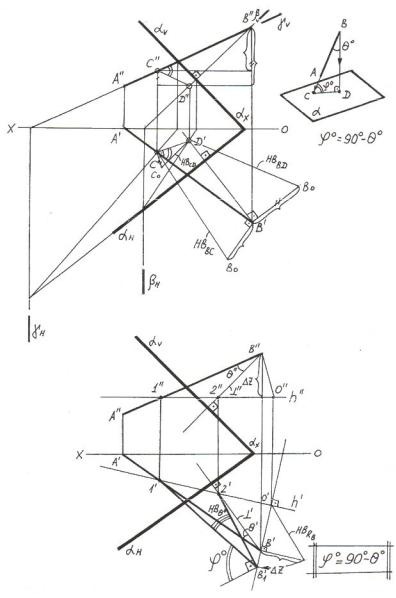
Рисунок 5.5 – Определение угла между прямой и плоскостью:

а – общегеометрическим методом; б – методом дополнительного угла

52

Более эффективным методом решения задачи является метод дополнительного угла. Дополнительным углом называется уголСВD, который образуется между заданной прямой и перпендикуляром, опущенным из любой точки прямой на заданную плоскость(см. дополнительную схему на рисунке5.5,а). Дополнительный угол СВD является вспомогательным углом, с помощью которого можно определить искомый угол. Искомый угол, как видно из схемы, может быть найден из математического выражения или графически, если достроить дополнительный угол до 90°.

На рисунке 5.5,б дано решение задачи методом дополнительного угла. Задача решается в такой последовательности:

-из точки В опускаем перпендикуляр на заданную плоскость;

-отмечаем проекции дополнительного угла;

-определяем натуральную величину дополнительного угла(например, методом вращения вокруг горизонтали);

-графическим путём достраиваем полученный дополнительный угол до 90° и получаем искомый угол.

5.5Определение угла между скрещивающимися прямыми

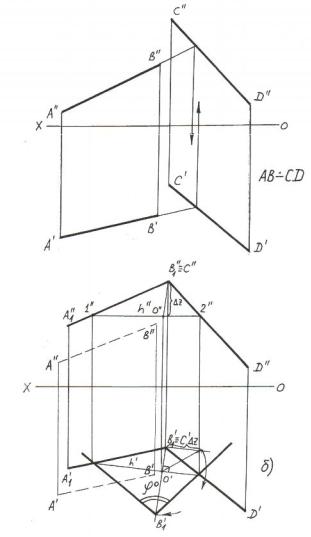
Угол между скрещивающимися прямыми (рисунок 5.6,а) является пространственным углом, в связи с чем его нельзя определить методами определения плоского угла без дополнительных преобразований. Путём преобразований угол между скрещивающимися прямыми можно привести к плоскому углу. Это осуществляют параллельным переносом одной из прямых в одну из точек другой прямой (в нашем примере прямая АВ параллельно перенесена в точку С прямой СD, точка В совмещена с точкой С). В результате описанного преобразования образуется плоский уголА1В1D1, натуральную величину которого можно определить описанным ранее методом(см. раздел 5.3.). На рисунке 5.6,б угол между двумя скрещивающимися прямыми определён методом вращения вокруг горизонтали.

53

а)

б)

Рисунок 5.6 – Определение угла между скрещивающимися прямыми

54

5.6Определение углов между плоскостью и плоскостями проекций

Общегеометрический метод решения упомянутой задачи заключается в том, что двугранные углы между плоскостью и плоскостями проекций заменяют плоскими углами, которые образуются с помощью линий наибольшего наклона к плоскостям проекци:йЛНН(Н), ЛНН(V) и ЛНН(W).

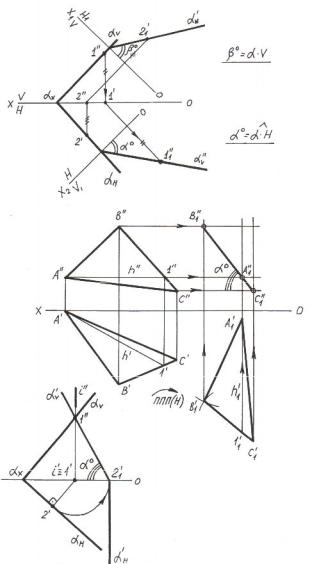
Углы между линиями наибольшего наклона и их соответствующими проекциями являются искомыми углами. ЛНН(Н) проводится перпендикулярно горизонтали или горизонтальному следу плоскости, ЛНН(V) – перпендикулярно фронтали или фронтальному следу плоскости, ЛНН(W) – перпендикулярно профильной прямой или профильному следу плоскости. После проведения в заданной плоскости линии наибольшего наклона угол её наклона к плоскости проекций может быть определён методом прямоугольного треугольника. На рисунке 5.7 представлено решение задачи на определение угла наклона плоскости треугольника АВС к плоскости проекций Н с помощью ЛНН(Н).

На рисунке 5.8 задача решена с помощью методов преобразования эпюра: методом перемены плоскостей проекций (рисунок 5.8,а), методом плоско-параллельного перемещения (рисунок 5.8,б) и методом вращения вокруг горизонтально-проецирующей оси i (рисунок 5.8,в). В последней задаче ось i проведена в произвольную точку1, взятую на фронтальном следе плоскости.

5.7Определение углов между двумя плоскостями

Угол между двумя плоскостями называется двугранным углом. Измерение двугранного угла на чертеже и на любой детали или конструкции представляет определённую сложность, так как он должен быть измерен строго в плоскости, перпендикулярной общему ребру двугранного угла (рисунок 5.9,а).

55

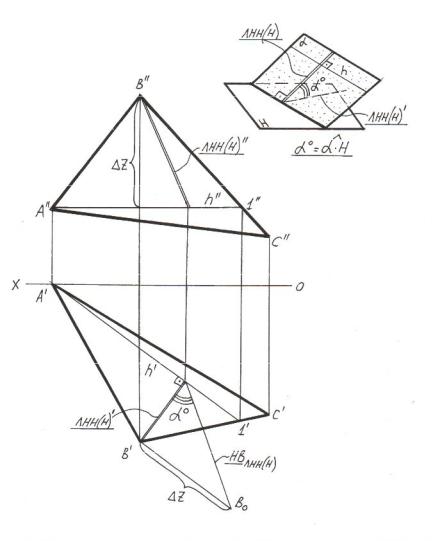
Рисунок 5.7 – Определение угла между плоскостью и плоскостью проекций с помощью линий наибольшего наклона

56

а)

б)

в)

Рисунок 5.8 – Определение угла между плоскостью и плоскостью проекций:

а – методом замены плоскостей проекций; б – методом плоско-параллельного перемещения; в – методом вращения вокруг проецирующих осей

57

а)

б)

в)

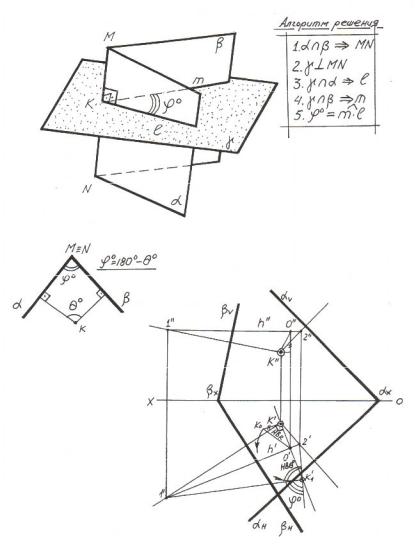
Рисунок 5.9 – Определение двугранного угла:

а – общегеометрическим методом; б, в – методом дополнительного угла

58

На этом рисунке представлен алгоритм решения задачи общегеометрическим методом. Алгоритм включает в себя следующие -по строения: находят линию пересечения граней угла; двугранный угол пересекают плоскостью, перпендикулярной общему ребру MN; нахо-

дят линии пересечения секущей плоскости с плоскостями граней (линии l и m); находят угол между линиями l и m, который будет являться искомым углом.

На рисунке 5.9,б представлена схема решения задачи методом дополнительного угла. Вывод формулы для определения двугранного угла ясен из рисунка. Если посмотреть вдоль общего ребра MN двугранного угла, то ребро «выродится» в точку, а грани угла – в линии. Угол между этими линиями – искомый угол. Если в створе угла взять любую точку и опустить из неё перпендикуляры на грани угла, то между перпендикулярами образуется угол, который называется дополнительным углом. Искомый двугранный угол может быть выражен через дополнительный угол как разность 180° и натуральной величины дополнительного угла.

На рисунке 5.9,в приведено решение задачи упомянутым методом. Натуральная величина дополнительного угла найдена методом вращения вокруг горизонтали. Двугранный угол между плоскостями найден графическим путём с учетом зависимости, приведённой на рисунке 5.9,б.

Наиболее эффективно задача на определение двугранного угла может быть решена методами преобразования, если общее ребро двугранного угла перевести из общего положения в проецирующее. При таком преобразовании общее ребро двугранного угла«вырождается» в точку, а грани угла – в линии. Угол между линиями является искомым двугранным углом.

На рисунке 5.10,а методом перемены плоскостей проекций определён двугранный угол при ребреВD, а на рисунке 5.10,б аналогичная задача решена методом плоско-параллельного перемещения.

59