
Metricheskie zadachi
.pdf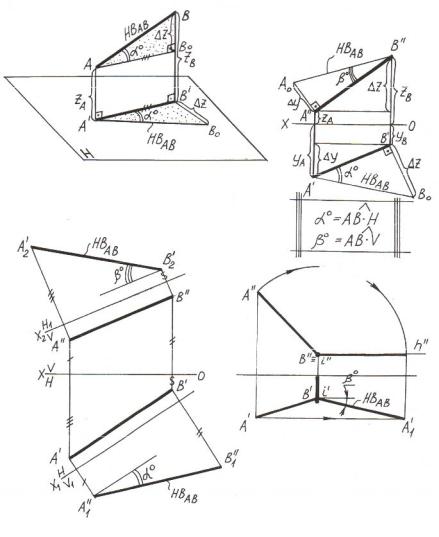
а) |
б) |
г)
в)
Рисунок 3.1 – Методы определения натуральной величины прямой по её проекциям
30
На рисунке 3.1,б приведён пример определенияНВ прямой АВ. Метод прямоугольного треугольника, как нетрудно убедиться из пространственного макета, позволяет одновременно определять углы наклона прямой к плоскостям проекций.
На рисунке 3.1,в натуральная величина прямой и углы её наклона к плоскостям проекций определены методом перемены плоскостей проекций.
На рисунке 3.1,г натуральная величина прямой и угол её наклона к плоскости проекций V определены методом вращения вокруг фрон- тально-проецирующей оси i.
3.2Определение натуральной величины плоских фигур
Как было показано ранее, плоские фигуры, расположенные в пространстве параллельно плоскости проекций, проецируются на эту плоскость в натуральную величину. Из этого свойства ортогонального проецирования следует вывод: для определения НВ плоской фигуры необходимо перевести её из общего положения в положение, параллельное какой-либо плоскости проекций, любым способом преобразования эпюра.
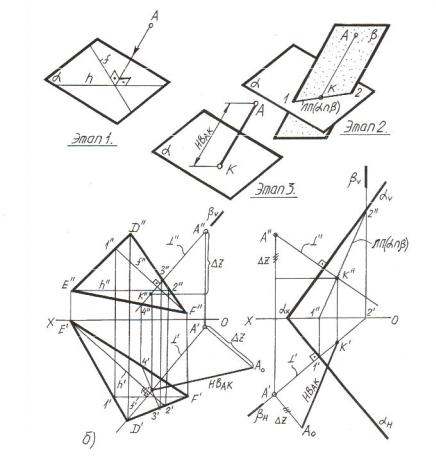
На рисунке 3.2,а приведён пример определения натуральной величины треугольника АВС методом вращения вокруг горизонтали. В задаче сторона ВС является горизонталью, в связи с чем метод вращения в данном случае является наиболее рациональным. При вращении будет перемещаться только точкаА. Натуральная величина радиуса вращения точки А определена методом прямоугольного треугольника. Натуральная величина радиуса вращения отложена вдоль плоскости вращения точки А и найдено конечное положение точки после вращения (А0).
На рисунке 3.2,б приведён пример определения НВ плоского угла методом перемены плоскостей проекций. Первой заменой V на V1 угол переводим во фронтально-проецирующее положение. Для этого в плоскости угла АВС проводим горизонталь и новую осьОХ1 располагаем перпендикулярно горизонтальной проекции горизонтали, в результате чего на новой фронтальной проекции плоскость угла «вырождается» в линию.
31

а)
б)
в)
Рисунок 3.2 – Методы определения натуральной величины плоских фигур
32
Второй заменой Н на Н1 плоскость угла располагаем параллельно новой плоскости проекций Н1, что позволяет получить натуральную величину угла на новой горизонтальной проекции угла.
На рисунке 3.2,в дан пример построения натуральной величины сечения шестигранной пирамиды. Пирамида усечена фронтальнопроецирующей плоскостью. В сечении пирамиды образуется многоугольник с эллипсом внутри от сечения отверстия. НВ сечения определена методом совмещения, т.е. вращением секущей плоскости вместе с расположенным в ней сечением вокруг горизонтального следа. Совмещённый фронтальный след при этом совпадает с осью ОХ. Ход построений ясен из рисунка.
33
4 МЕТРИЧЕСКИЕ ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ
МЕЖДУ ГЕОМЕТРИЧЕСКИМИ ОБЪЕКТАМИ
4.1 Определение расстояния между двумя точками
Задача на определение расстояния между двумя точками сводится к определению натуральной величины прямой, соединяющей заданные точки.
Расстояние между двумя точками– это, по сути дела, основная метрическая задача, так как большинство метрических задач в -ко нечном итоге сводится к решению этой основной задачи. Методы определения натуральной величины прямой изложены в разделе 3.1.
4.2 Определение расстояния от точки до плоскости
Рассмотрим общегеометрический метод решения задачи(рисунок 4.1,а). Решение задачи сводится к таким последовательным логическим действиям:
-из заданной точки опускаем перпендикуляр на заданную плоскость;
-находим точку встречи перпендикуляра с плоскостью (точка K);
-определяем натуральную величину расстояния между точками А и K.
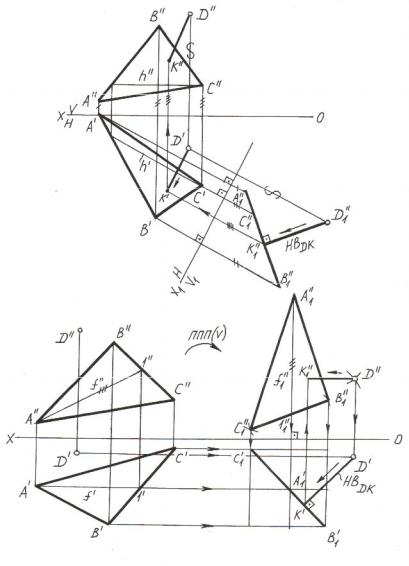
Эта схема решения задачи реализована в примерах на рисунках 4.1,б, в. В первой задаче проекции перпендикуляра проведены с помощью горизонтали и фронтали, проведённых в плоскости заданного треугольника. Во второй задаче проекции перпендикуляра проведены перпендикулярно следам плоскости в соответствии с алгоритмом проведения перпендикуляра к плоскости. Точки встречи перпендикуляра с плоскостью в обеих задачах определены с помощью вспомогательных плоскостей в соответствии с методикой решения задачи о пересечении прямой с плоскостью (см. раздел «Позиционные задачи» курса начертательной геометрии). Натуральная величина искомого расстояния определена методом прямоугольного треугольника.
34
а)
б) |
в) |
|
|
Рисунок 4.1 – Определение расстояния от точки до плоскости общегеометрическим методом
35
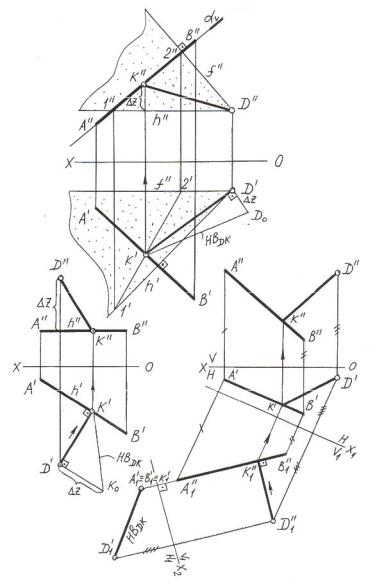
На рисунке 4.2,а рассмотрена задача на определение расстояния от точки до плоскости с использованием метода перемены плоскостей проекций. На рисунке 4.2,б аналогичная задача решена методом плоско-параллельного перемещения. В обеих задачах смысл решения сводится к следующему: чтобы реально увидеть в пространстве расстояние от точки до плоскости необходимо так установить направление взгляда, чтобы плоскость «выродилась» в линию. Тогда расстояние от точки до плоскости найдётся с помощью перпендикуляра, опущенного из точки на «вырожденную» линию плоскости. В связи с этим для решения задачи обоими методами необходимо перевести заданную плоскость из общего положения в проецирующее.
В первой задаче это достигнуто заменойV на V1, причем плоскость V1 располагаем перпендикулярно горизонтальной проекции горизонтали, в результате чего заданная плоскость становится фрон- тально-проецирующей.
Во второй задаче плоскость общего положения переведена в гори- зонтально-проецирующее положение путём плоско-параллельного перемещения относительно плоскости V так, чтобы фронталь f, проведённая в треугольникеАВС, стала перпендикулярной осиОХ, а следовательно, и плоскости проекций Н.
4.3 Определение расстояния от точки до прямой
Расстояние от точки до прямой измеряется с помощью перпендикуляра, опущенного из заданной точки на прямую.
Если прямая является прямой частного положения, то перпендикуляр проводится согласно теореме прямого угла (рисунок 4.3,а).
Если прямая занимает общее положение, то задача осложняется, так как в этом случае необходимо использовать специальные методы.
Общегеометрический метод (рисунок 4.3,б) предполагает следующие этапы решения задачи:
- через точку D проводим плоскость, перпендикулярную прямой АВ. Плоскость задаём пересекающимися горизонталью h и фронталью f. Их проекции проводим согласно алгоритму проведения перпендикуляра к плоскости (обратная задача);
36
а)
б)
Рисунок 4.2 – Определение расстояния от точки до плоскости методами преобразования эпюра
37
- находим точку встречи прямой АВ с проведённой плоскостью с помощью вспомогательной плоскости. Далее находим линию пересечения обеих плоскостей. Там, где линия 1–2 пересекает прямую АВ, находим точку встречи K;
-точки D и K соединяем, получаем проекции искомого перпендикуляра, т.е. проекции кратчайшего расстояния от точки до прямой;
-методом прямоугольного треугольника находимНВ расстоя-
ния.
На рисунке 4.3, представлено решение задачи методом перемены плоскостей проекций. Решение основано на том, что расстояние от точки до прямой определится, если посмотреть вдоль прямой линии.
Тогда прямая «выродится» в точку, а расстояние между двумя точками будет искомым. Таким образом, задача решается путём перевода прямой общего положения в проецирующее положение. Ход решения задачи ясен из чертежа.
4.4Расстояние между параллельными прямыми и плоскостями
Расстояние между параллельными прямыми и параллельными плоскостями определяется величиной перпендикуляра, опущенного из любой точки одной прямой или плоскости на другую прямую или плоскость.
Этот общегеометрический способ, аналогичный определению расстояния от точки до прямой или от точки до плоскости (см. разделы 4.2 и 4.3), достаточно трудоёмок, в связи с чем для решения упомянутых задач наиболее целесообразно применять методы преобразования эпюра.
Расстояние между двумя параллельными прямыми или двумя параллельными плоскостями определится, если направить взгляд вдоль прямых или плоскостей. При этом прямые «вырождаются» в точки, а плоскости – в линии. Расстояния между «вырожденными» точками или линиями являются искомыми расстояниями.
38
б)
а)
в)
Рисунок 4.3 – Определение расстояния от точки до прямой
39
