
Metricheskie zadachi
.pdf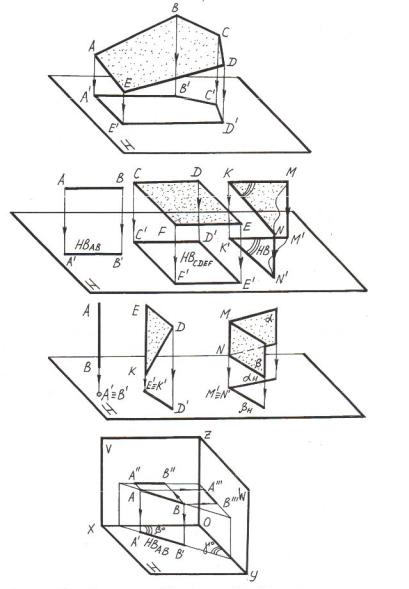
а)
б)
в)
г)
Рисунок 1.2 – Метрические свойства ортогонального проецирования
10
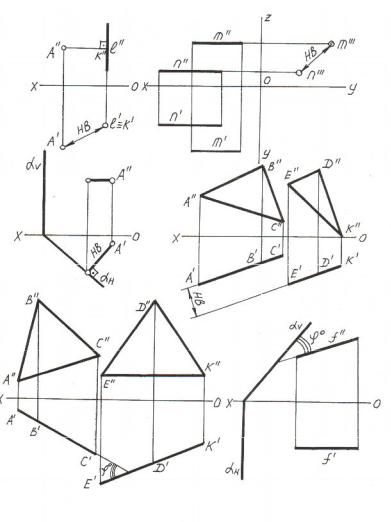
-плоская фигура или плоский угол, параллельные плоскости проекций, проецируются на эту плоскость в натуральную величину (см. рисунок 2.1,б);
-если плоская фигура и плоский угол перпендикулярны плоскости проекций, то они проецируются на эту плоскость в виде прямой линии («вырождаются» в линию) (см. рисунок 2.1,в);
-расстояние между геометрическими объектами изображается на проекциях в натуральную величину, если это расстояние параллельно плоскости проекций;
-расстояние от точки до прямой изображается на проекциях в натуральную величину, если прямая является проецирующей прямой
и«вырождается» на одной из проекций в точку. На рисунке 2.2,а показано расстояние между точкой и фронтально-проецирующей прямой;
-расстояние между параллельными прямыми изображается в натуральную величину, если они являются проецирующими и«вырождаются» на одной из проекций в точки (см. рисунок 2.2,б);
-расстояние от точки до плоскости изображается в натуральную величину, если плоскость является проецирующей и на одной из проекций «вырождается» в линию (см. рисунок 2.2,в);
-расстояние между двумя параллельными плоскостями изображается в натуральную величину, если плоскости являются одно- имённо-проецирующими и «вырождаются» на одной из проекций в линии (рисунок 2.2,г);
-угол между прямой и плоскостью изображается в натуральную величину, если плоскость является проецирующей, а прямая – линией уровня. В задаче на рисунке 2.2,д определён угол между фронталью и фронтально-проецирующей плоскостью;
-угол между двумя плоскостями изображается в натуральную величину, если обе плоскости являются одноимённо-проецирую- щими (или если их общее ребро является проецирующим) (см. рису-
нок 2.2,е);
-плоско-параллельный перенос геометрического объекта или плоскости проекций не изменяет вида и размеров проекции объекта.
11
а)
в)
б)
г)
д)
е)
Рисунок 2.2 – Частные случаи определения расстояний и углов между геометрическими объектами
12
а)

2.2 Теорема прямого угла
Теорема прямого угла является одной из основных теорем, определяющих многие построения в метрических задачах. Теорема заключается в следующем.
Пусть в пространстве имеется прямой уголАВС. Один катет АВ параллелен какой-либо плоскости Q, другой катет не параллелен и не перпендикулярен упомянутой плоскости (рисунок 2.3).
В пространстве угол АВС прямой. Докажем, что угол А/В/С/ тоже прямой. Фигура АВВ/А/ – прямоугольник, следовательно, отрезок АВ перпендикулярен проецирующей плоскости ВСС/В/, так как он перпендикулярен двум пересекающимся прямым ВС и ВВ/ по условию и построению. Но АВ параллельна А/В/, следовательно, А/В/ перпендикулярна плоскости ВСС/В/, поэтому А/В/ перпендикулярна В/С/, т.е. угол А/В/С/ равняется 90°.
Таким образом, если один катет прямого угла параллелен какойлибо плоскости (или плоскости проекций), а другой катет не параллелен и не перпендикулярен упомянутой плоскости, то прямой угол проецируется на эту плоскость в натуральную величину, т.е. в 90°.
Теорема прямого угла распространяется не только на пересекающиеся перпендикулярные прямые (рисунок 2.4,а), но и на перпендикулярные скрещивающиеся прямые (рисунок 2.4,б).
2.3 Перпендикуляр к плоскости
Из курса элементарной геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум любым пересекающимся прямым, находящимся в этой плоскости. Проведение перпендикуляра к плоскости (опускание перпендикуляра) и восстановление перпендикуляра из плоскости называется прямой задачей. Проведение плоскости перпендикулярно заданной прямой называется обратной задачей. В обоих случаях прямой задачи для того, чтобы опустить перпендикуляр на плоскость или восстановить (восставить) его из плоскости, необходимо в плоскости провести две пересекающиеся прямые, с помощью которых можно провести перпендикуляр к плоскости. При решении обратной задачи плоскость задают двумя пересекающимися прямыми или следами.
13
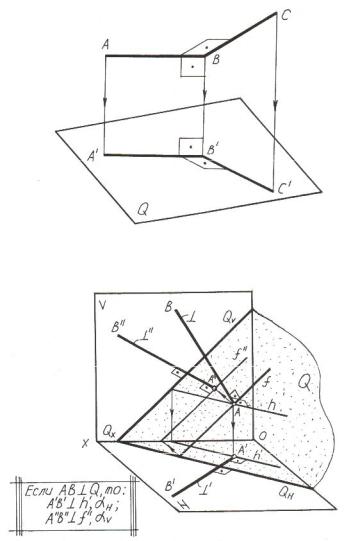
Рисунок 2.3 – Теорема прямого угла
Рисунок 2.5 – Вывод алгоритма проведения перпендикуляра к плоскости
14
а)
б)
Рисунок 2.4 – Использование теоремы прямого угла для пересекающихся и скрещивающихся прямых
15
Так как в начертательной геометрии рассматриваются не сами геометрические объекты, а их проекции, то необходимо рассмотреть вопрос о том, как проводить проекции перпендикуляра к плоскости. Для разработки алгоритма проведения проекций перпендикуляра к плоскости рассмотрим пространственный макет двух плоскостей проекций, в системе которых расположена плоскость общего положения Q (рисунок 2.5).
Возьмём в плоскости Q любую точку А и восстановим из неё перпендикуляр. Для этого в плоскости надо предварительно провести две пересекающиеся прямые. Наиболее целесообразно в качестве этих прямых взять горизонталь h и фронталь f.
Далее из точки А восстановим перпендикуляр так, чтобы он был перпендикулярен горизонтали и фронтали. Спроецируем точку А на плоскости проекций H и V. Из проекций точки А проведём горизонтальную и фронтальную проекции перпендикуляра.
В соответствии с теоремой прямого угла и исходя из пространственного макета проекции перпендикуляра должны быть проведены следующим образом:
-горизонтальная проекция перпендикуляра проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу плоскости;
-фронтальная проекция перпендикуляра проводится перпендикулярно фронтальной проекции фронтали или фронтальному следу плоскости.
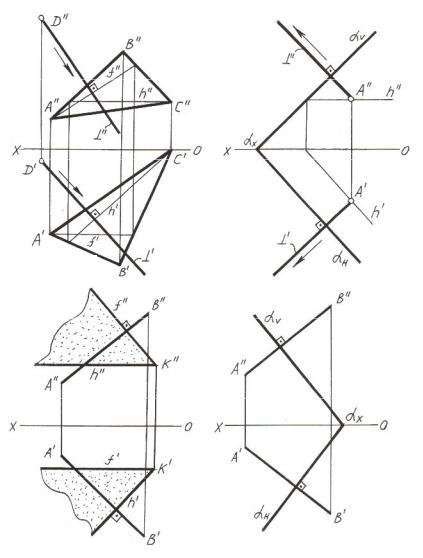
Правило проведения перпендикуляра к плоскости в алгоритмической форме записано на рисунке2.5. Если использовать алгоритм в направлении «слева-направо», то он позволяет решать прямую задачу, т.е. опускать перпендикуляр на плоскость или восстанавливать его из плоскости. Если использовать алгоритм в направлении«спра- ва-налево», то он позволяет проводить плоскость, перпендикулярную заданной прямой. На рисунке 2.6 представлены примеры решения прямой и обратной задач. На рисунке 2.6,а из точки D опущен перпендикуляр на плоскость треугольникаАВС. На рисунке 2.6,б из произвольной точки А, принадлежащей плоскости, заданной следами, восстановлен перпендикуляр, проекции которого проведены перпендикулярно следам заданной плоскости.
16
б)
а)
г)
в)
Рисунок 2.6 – Примеры решения прямой и обратной задач о перпендикуляре к плоскости
17
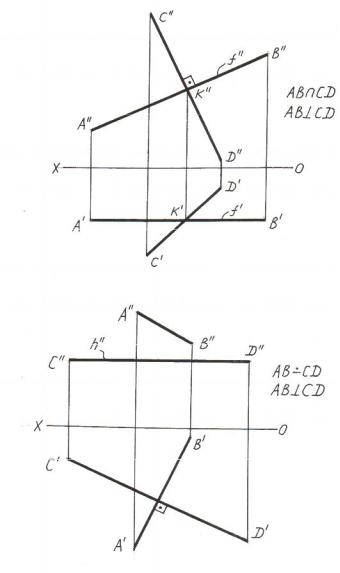
На рисунке 2.6,в, г показано, как надо проводить плоскость, проходящую через точкуK перпендикулярно заданной прямойАВ. В первом случае плоскость задана двумя пересекающимися прямыми – горизонталью и фронталью, а в другом случае – следами.
2.4 Перпендикулярность двух прямых
Перпендикулярность двух прямых частично рассмотрена в теореме прямого угла. Однако теорема прямого угла может быть использована лишь в том случае, когда один из катетов прямого угла параллелен какой-либо плоскости проекций.
Задача осложняется, если катеты прямого угла являются прямыми общего положения. В этом случае ни на одной проекции угол не изображается в натуральную величину.
Для решения задачи целесообразно использовать методы преобразования с целью перевода одной из сторон прямого угла из общего положения в частное.
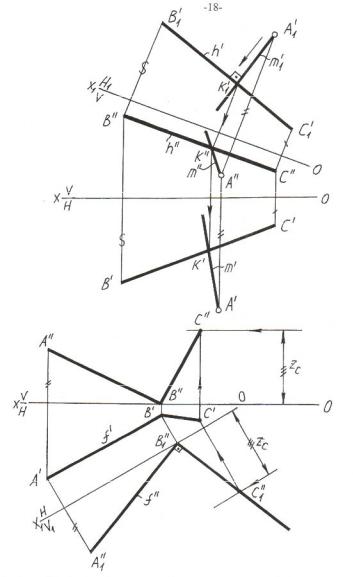
На рисунке 2.7,а представлено построение прямойm, проведённой через точку А перпендикулярно прямой ВС и пересекающей её в точке K. Задача решена методом перемены плоскостей проекций (заменой Н на Н1). В новой системе плоскостей проекций прямаяВС становится горизонталью, в связи с чем из новой горизонтальной проекции точки на основании теоремы прямого угла можно опустить перпендикуляр на прямую ВС.
На рисунке 2.7,б представлено решение задачи о построении прямого угла АВС, если заданы проекции стороны АВ.
Заменой плоскости V на V1 переводим прямую общего положения АВ в положение фронтали. Далее на основании теоремы прямого угла из точки В1// под углом 90° проводим направление другой стороны прямого угла, на которой берём произвольную точкуС1//, затем – произвольную точку С/. Точку С// находим с помощью аппликаты точки С.
Далее будет рассмотрен другой способ построения двух перпендикулярных прямых общего положения.
18
а)
б)
Рисунок 2.7 – Построение прямого угла между прямыми общего положения методом перемены плоскостей проекций
19
