Metricheskie zadachi

2.5 Перпендикулярность двух плоскостей

Из элементарной геометрии известно, что две плоскости будут взаимно перпендикулярными, если одна из них содержит прямую, перпендикулярную другой плоскости.

Поэтому построение плоскости, перпендикулярной заданной плоскости, можно провести двумя способами:

-проводим прямую, перпендикулярную заданной плоскости, затем через прямую проводим плоскость, перпендикулярную заданной плоскости;

-проводим прямую, принадлежащую или параллельную заданной плоскости, затем строим плоскость, перпендикулярную проведённой прямой.

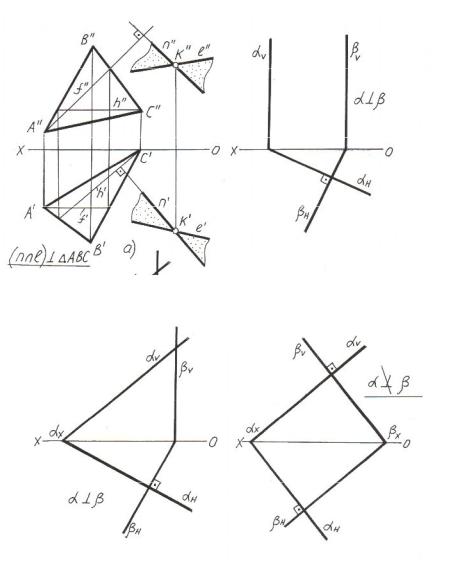
На рисунке 2.8,а представлена задача: через прямую l провести плоскость, перпендикулярную плоскости треугольникаАВС. Решение задачи: на прямой берём произвольную точкуK. Из точки K опускаем перпендикуляр на плоскость АВС, проведя предварительно в плоскости треугольника горизонталь и фронталь. Через точку K проводим ещё одну произвольную прямуюn. Две пересекающиеся прямые l и n задают искомую плоскость.

Если плоскости заданы следами, то возможны следующие случаи:

- две плоскости перпендикулярны, если они одноимённопроецирующие и их«собирательные» следы взаимно перпендикулярны (рисунок 2.8,б). Напомним, что «собирательный» след – это след проецирующей плоскости, который не перпендикулярен оси ОХ;

-плоскость общего положения и проецирующая плоскость перпендикулярны, если «собирательный» след проецирующей плоскости перпендикулярен одноимённому следу плоскости общего положения;

-если одноимённые следы двух плоскостей общего положения взаимно перпендикулярны, то это не является достаточным условием перпендикулярности плоскостей (рисунок 2.8,г).

20

г)

в)

Рисунок 2.8 – Примеры построения перпендикулярных плоскостей (а, б, в); г – неперпендикулярность двух плоскостей общего положения

21

2.6Использование методов преобразования в метрических задачах

Методы преобразования эпюра Монжа предназначены для перевода геометрических объектов из общего положения в частное, что значительно упрощает решение метрических задач по сравнению с использованием общегеометрических методов.

При решении метрических задач используются практически все методы преобразования: метод перемены плоскостей проекций, метод вращения вокруг проецирующих осей, метод вращения вокруг горизонтали или фронтали, метод совмещения и метод плоскопараллельного перемещения.

В настоящих методических указаниях приведены лишь краткие сведения о методах преобразования эпюра.

Метод перемены (замены) плоскостей проекций заключается в том, что геометрический объект остаётся неподвижным, а плоскости проекций заменяются другими плоскостями так, чтобы в новой системе плоскостей проекций геометрический объект стал занимать частное положение, т.е. параллельное или перпендикулярное новым плоскостям проекций.

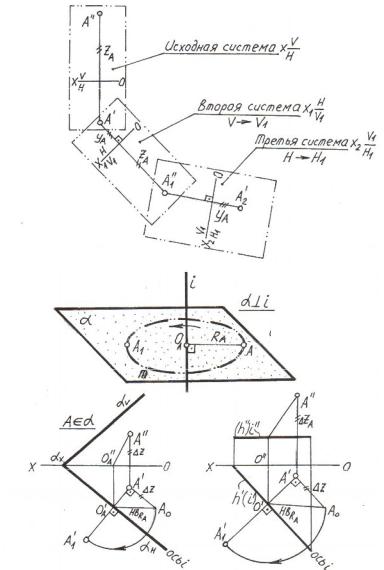
Для того чтобы построить новую проекцию точки при замене V на V1, необходимо от новой оси по новой линии связи отложить аппликату точки, взятой из предыдущей системы плоскостей проекций, а при замене Н на Н1 – ординату точки (рисунок 2.9,а).

Метод вращения вокруг проецирующей оси, вокруг следов плоскости (метод совмещения) и вокруг горизонтали или фронтали -за ключается в том, что геометрический объект вращают вокруг упомянутых осей до тех пор, пока он не займёт частное положение относительно неподвижных плоскостей проекций. Все методы вращения основываются на общих закономерностях вращения, называемых параметрами вращения (рисунок 2.9,б). К ним относятся ось вращения i, объект вращения А, плоскость вращения, центр вращения О, радиус вращения точки RА и траектория вращения m точки. Плоскость вращения всегда проводится перпендикулярно оси вращения.

22

а)

б)

г)

в)

Рисунок 2.9 – Методы преобразования эпюра:

а – метод перемены плоскостей проекций; б – метод вращения вокруг проецирующих осей; в – метод совмещения; г – метод вращения вокруг горизонтали

23

Для того чтобы определить конечное положение точки после вращения, необходимо отложить от центра вращения вдоль плоскости вращения радиус вращения точки в натуральной величине.

На рисунке 2.9,в показано вращение вокруг следа плоскости, на рисунке 2.9,г – вращение вокруг горизонтали.

Метод плоско-параллельного перемещения основан на плоскопараллельном движении объекта, при котором каждая его точка перемещается в плоскостях, параллельных какой-либо плоскости проекций. Различают плоско-параллельное перемещение относительно плоскости Н и относительно плоскости V – соответственно ППП(Н) и

ППП(V).

При ППП(Н) горизонтальная проекция объекта меняет своё положение, но не меняет своей конфигурации. Фронтальная проекция объекта меняет свою конфигурацию и каждая его точка перемещается по линиям, параллельным оси ОХ. При ППП(V) наблюдается противоположная картина.

Метод плоско-параллельного перемещения заключается в ,том что объект перемещают в пространстве плоско-параллельно так, чтобы он стал занимать частное положение относительно плоскостей проекций. Можно совершать одно или два плоско-параллельных перемещения.

Основными задачами методов преобразования являются:

-перевод прямой общего положения в положение горизонтали или фронтали;

-перевод прямой общего положения в проецирующее положение;

-преобразование плоскости общего положения в горизонтальную или фронтальную плоскость;

-преобразование плоскости общего положения в проецирующую плоскость (перпендикулярную Н или V).

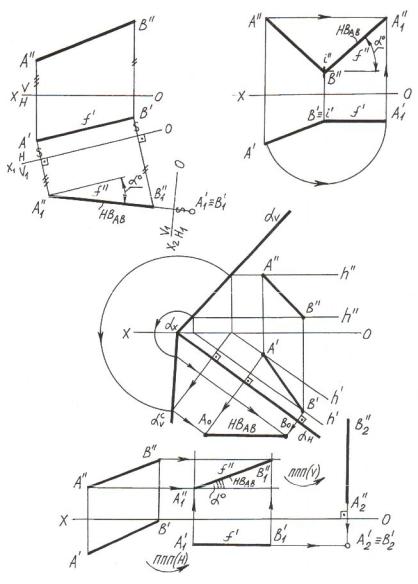
Приведём примеры вышеупомянутых преобразований. На рисунке 2.10 представлены методы перевода прямой общего положения в частное. На рисунке 2.10,а прямая общего положенияАВ путём замены V на V1 сначала переведена в положение фронтали (определены её натуральная величина и угол наклона к плоскостиН). Затем заменой Н на Н1 прямая преобразована в горизонтально-проецирующую прямую и «вырождена» в точку.

24

б)

а)

в)

г)

Рисунок 2.10 – Примеры преобразования прямой общего положения в прямую частного положения

25

На рисунке 2.10,б методом вращения вокруг горизонтально-про- ецирующей оси i прямая переведена из общего положения в частное и определены её натуральная величина и угол наклона к плоскости Н.

На рисунке 2.10,в методом совмещения заданной плоскости с плоскостью проекций Н определена натуральная величина прямой общего положения, принадлежащей плоскости. Построения ясны из приведённого чертежа.

На рисунке 2.10,г методом плоско-параллельного перемещения

ППП(Н) прямая общего положения переведена в положение фронтали (определены НВ прямой и угол наклона её к плоскости Н), а затем методом ППП(V) прямая преобразована в горизонтально-проеци- рующую прямую.

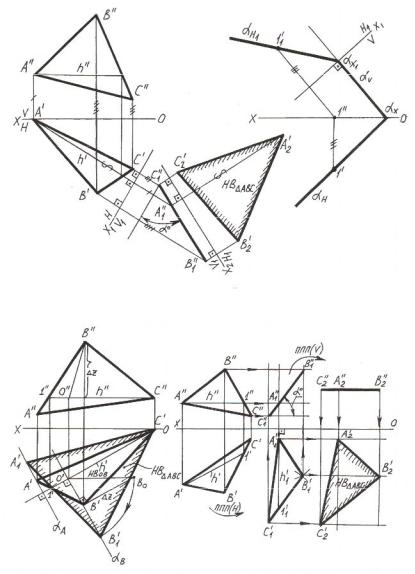
Перевод плоскости общего положения в плоскость частного положения представлен на рисунке2.11. Так, например, на рисунке2.11,а осуществлено преобразование плоскости АВС методом перемены плоскостей проекций. Сначала плоскость АВС преобразована во фронталь- но-проецирующую плоскость путём заменыV на V1. Для того чтобы плоскость стала фронтально-проецирующей, т.е. перпендикулярной новой плоскости V1, она должна содержать прямую, перпендикулярную V1.

В качестве такой прямой взята горизонтальh. После первой замены треугольник «вырождается» в линию. Второй заменой Н на Н1 плоскость АВС переведена в горизонтальную плоскость. Новая горизонтальная проекция треугольника является его натуральной величиной.

На рисунке 2.11,б представлено преобразование плоскости, заданной следами, в горизонтально-проецирующую плоскость методом замены плоскостей проекций. Новую плоскость проекций Н1 располагаем перпендикулярно фронтальному следу плоскости. С помощью точки 1, взятой произвольно на горизонтальном следе, строим новый горизонтальный след искомой плоскости.

На рисунке 2.11,в показано преобразование плоскости треугольника АВС в горизонтальную плоскость путём вращения его вокруг горизонтали. По окончании вращения плоскость треугольника становится параллельной плоскости проекций Н, и его новая горизонтальная проекция является натуральной величиной. На рисунке 2.11 представлены все параметры вращения: ось вращения, объекты вращения (точки А и В), плоскости вращения точек, центры их вращения, радиусы вращения и новое положение точек.

26

б)

а)

в)

г)

Рисунок 2.11 – Примеры преобразования плоскости общего положения в частное

27

На рисунке 2.11,г изображено преобразование треугольникаАВС сначала во фронтально-проецирующую плоскость методом ППП(Н), а затем – в горизонтальную плоскость методом ППП(V). После первого перемещения треугольник «вырождается» в линию, что позво-

ляет определить угол наклона плоскости треугольника к плоскости проекций Н. В результате второго перемещения определяется натуральная величина треугольника.

Все вышерассмотренные основные методики и положения являются теоретической основой решения всего многообразия метрических задач. В связи с этим изучение темы «Метрические задачи» необходимо начать с изучения теоретических основ начертательной геометрии.

28

3 МЕТРИЧЕСКИЕ ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ

ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ

3.1 Определение натуральной величины прямой

Основополагающим методом определения натуральной величины прямой по её проекциям является метод прямоугольного треугольника. Для пояснения метода рассмотрим пространственный макет (рисунок 3.1,а). Пусть в пространстве имеется прямая общего положения АВ. Спроецируем прямую на плоскость проекций Н. Получим горизонтальную проекцию прямой А/В/.

Она будет меньше самой прямой. Как же определить НВ прямой по её проекциям? Рассмотрим треугольник АВВ0 (в пространстве).

Треугольник АВВ0 – прямоугольный. Один катет треугольника равен горизонтальной проекции прямой. Другой катет является разностью аппликат концов отрезка АВ. Гипотенуза является натуральной величиной прямой.

Если этот треугольник построить на горизонтальной проекции прямой, то из него можно графически определитьНВАВ. Аналогично можно определить натуральную величину прямой и на других её проекциях. Таким образом, исходя из пространственного макета, можно сформулировать общее правило: для того чтобы определить НВ отрезка прямой по её проекциям, необходимо на одной из её проекций (на любой) построить прямоугольный треугольник, одним катетом которого является сама проекция прямой, а другим катетом – разность недостающих координат концов отрезка, тогда гипотенуза треугольника будет являться натуральной величиной отрезка прямой . Недостающей координатой является та координата, которая не участвует в построении проекции прямой. Например, горизонтальная проекция точки строится по координатамх и y, фронтальная проек-

ция – по х и z, профильная – по z и у. Координаты z, у и х соответственно являются недостающими.

29