
- •Типы решений
- •HFSS IE решатель
- •Гибридный метод конечных элементов и интегральных уравнений (FEBI)
- •Проблемы многоядерности
- •Производительность
- •Функциональные возможности
- •Проблемы параллельного программирования
- •Языки программирования
- •Специализированные библиотеки
- •Лекция 4 ТО САПР, ч.2
- •Адресация в сетях ТСР/IP.
- •- эскизирование с учетом ограничений. Чертеж временного характера, выполненный на любом материале от руки, в глазомерном масштабе, но с соблюдением пропорций элементов детали, называется эскизом.
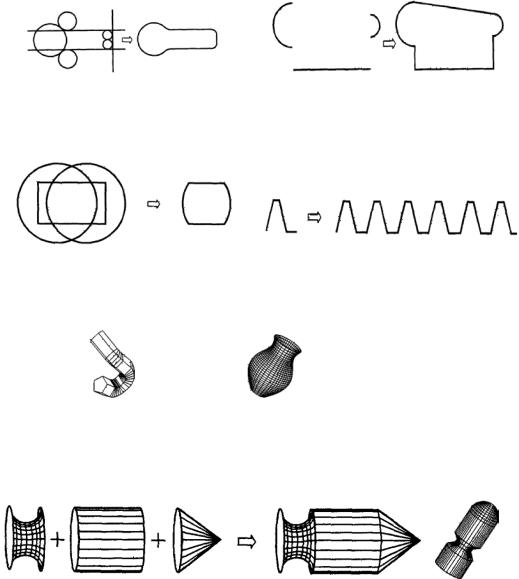
В математическом аппарате пакетов твердотельного моделирования реализованы функции построения поверхностей по образующим линиям. Конструктору предлагается обширный инструментарий создания и редактирования двумерных примитивов (прямых, дуг, окружностей, многоугольников и т.д.) и сложных контуров. Эти поверхности преобразуются в тела ограниченного объема и используются в топологических операциях с телами. Большинство машиностроительных деталей строится с использованием сложных формообразующих контуров. Рассмотрим некоторые способы получения сложного контура:
а) получение сложного контура по вспомогательным пересекающимся или касательным линиям. Возможно построение сложного контура одной полилинией за одну операцию.
б) Построение сложного контура с использованием непересекающихся дуг и отрезка
а) |
б) |
в) Формирование контура в результате топологических операций над замкнутыми контурами. Получение сложного контура в результате топологических операций пересечения прямоугольника и двух окружностей.
Получение сложного контура в результате применения к линейным элементам матрицы преобразований (сдвиг, поворот, копирование массивом и т.д.). г) получение незамкнутого контура как линейного массива шести копий исходного контура
в) |
г) |
Кроме функций построения базовых тел в пакетах твердотельного моделирования реализованы различные функции создания тел сложной внешней формы. Это так называемые кинематические тела протягивания и вращения. В качестве формообразующих могут использоваться кривые, двумерные примитивы, сложные замкнутые или незамкнутые контуры.
Рис. Кинематическое тело протягивания Рис. Тело вращения
Принципиальным становится этап концептуальной разработки изделия, анализа будущего изделия при наименьших затратах времени и других ресурсов. Концептуальная геометрическая модель задает скорость и низкую себестоимость процесса ее разработки, технологичность и удобство последующего использования. Процедура преобразования исходной модели в новую модель изделия называется модификация. Модификация модели зависит от способа ее построения и базируется на истории создания твердого тела.
Твердотельное моделирование наиболее часто используется в следующих случаях:
-при проектировании типовых деталей и узлов машиностроительных изделий
-для выполнения модификации модели с использованием истории ее создания
-для оценки свойств проектируемых деталей - площадь поверхности, масса, центр тяжести и т.п.
-для контроля взаимного расположения деталей и работы механизма
-для автоматизации подготовки КД и ТД с последующей обработкой на станках с ЧПУ
Когда конструкция будущей машины проработана в эскизах, определены размеры рабочих органов, рассчитаны нагрузки, то можно переходить к твердотельному моделированию отдельных деталей и сборок будущей машины. Наиболее удобной CAD – системой твердотельного моделирования являются для низшего класса AutoCAD, для среднего
SolidWorks/SolidEdge, КОМПАС-3D.
- эскизирование с учетом ограничений. Чертеж временного характера, выполненный на любом материале от руки, в глазомерном масштабе, но с соблюдением пропорций элементов детали, называется эскизом.
Существуют ограничения формы – это отношения между элементами контура (например, перпендикулярность между двумя линиями, касание между дугой и линией и т. п.) и размеров (система генерирует точный контур, удовлетворяющий данным размерам). Изменение геометрических ограничений и/или размеров приводит к различным телам, получаемых в результате данных операций. Этот подход и называется параметрическим моделированием, потому что различные тела
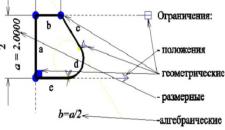
генерируются путем изменения параметров. Параметрами могут быть некоторые константы, входящие в геометрические и/или размерные ограничения, алгебраические ограничения. Ограничения (равно как и декларативные конструктивные элементы) не основаны на истории построения - т.е. при трансляции в другую систему нужно просто передать список ограничений вместе с геометрией - и все.
Параметрическое моделирование (параметризация) — моделирование (проектирование) с использованием параметров элементов модели и соотношений между этими параметрами. Конструктор в случае параметрического проектирования создаёт математическую модель объектов с параметрами, при изменении которых происходят изменения конфигурации детали, взаимные перемещения деталей в сборке. Параметризация позволяет за короткое время «проиграть» (с помощью изменения параметров или геометрических отношений) различные конструктивные схемы и избежать принципиальных ошибок.
Идея параметрического моделирования появилась ещё на ранних этапах развития САПР, но долгое время не могла быть осуществлена по причине недостаточной компьютерной производительности. Существует 3 подхода к созданию параметризованной геометрической модели изделия:
1.параметрическое конструирование (ПК); возможность создания геометрических моделей с использованием связей и правил, которые могут переопределяться и дополняться на любом этапе ее создания. Связи определяется в виде размерных, геометрических, алгебраических соотношений. Правила определяются как условия выполнения базовой операции.
2.ассоциативная геометрия (АГ) базируется на непосредственной взаимосвязи между объектами и создается на таких понятиях как параллельность, перпендикулярность, соосность, вертикальность, концентричность и пр.
3.объектно-ориентированное конструирование с использованием базовых операций добавления (удаление)
материала. Этот подход реализован на основе определенного набора правил и атрибутов, задаваемых при выполнении базовой операции в дополнение к уже заданным связям и ассоциативной геометрии. Например: сквозное отверстие - вычитание, причем под сквозным отверстием понимается правило, которое определяет сквозной проход в заданном месте через тело модели независимо от того, изменялась форма модели, или нет. После выполнения базовой операции ее топология должна сохраняться и распознаваться как базовая операция (отверстие, паз, округление), а также предоставлять возможность изменения определяющих ее геометрических параметров.
Параметризация модели основана на истории построения. История построения имеет иерархическую структуру и представляется в виде «дерева» построения. Она включает описание всех элементов, используемых для построения тела, параметры и последовательность выполненных операций. На нижнем уровне размещаются геометрические примитивы (плоские или объемные), параметры примитивов. На всех последующих уровнях могут размещаться сборки тел, полученные в результате преобразований над объектами нижнего уровня, а также промежуточные результаты топологических операций над отдельными конструктивными элементами. На верхнем уровне истории создания всегда находится результирующее тело (сборка, узел или агрегат).
Эта информация теряется при переносе из одной системы в другую. Нынешние трансляторы IGES и STEP не работают с описаниями ограниченных условий и историй, поэтому последующее редактирование создаваемых объектов становится затруднительным. Для обеспечения эффективной трансляции геометрических 3D моделей между различными CAD системами приходится разрабатывать специальные трансляторы, например программный комплекс 3DTransVidia (компания ТЕСИС, Россия).
Известным недостатком параметризации на основе истории построения является необходимость принятия решения о том, какие параметры модели могут быть изменены, прямо во время создания модели. Если позже по каким-то причинам пользователю нужно будет изменить параметр, который отсутствует в дереве, решение будет нелегким: переделать модель с нуля, либо использовать сложные оптимизационные алгоритмы в попытке подобрать желаемое значение искомого параметра путем варьирования значений параметров, определяющих модель. История построения обычно теряется при трансляции из одного формата CAD в другой. Транслируется только граничная модель тела, которая в таком случае называется «немой» геометрией.
Фичерсы — параметризованные объекты, привязанные к определенному геометрическому контексту. При модификации модели привязка сохраняется с соответствующей корректировкой фичерсов. Фичерсы — привычные пользователю конструкционно-технические элементы, такие как отверстия, фаски, скругления, ребра жесткости, центральные отверстия, канавки, которые помнят о своем окружении независимо от внесенных изменений. Возможно автоматически создавать любой объект и элемент (фаски, скругления) просто указывая их местоположение. После этого они остаются привязанными к грани при любом ее перемещении.
На рис. 18. показаны типовые технологические параметризованные макроэлементы – скругление (рис. 18. а), фаска
рис. 18. б), сквозное отверстие рис. 18. в), вырез рис. 18. г), выступ рис. 18. д), бобышка рис. 18. е). Преимущества параметрического моделирования особенно сильно проявляются при модификации полученного тела. Например, при увеличении высоты исходного параллелепипеда на рис. 18. в), высота отверстия также увеличится и оно останется сквозным. При использовании классического твердотельного моделирования отверстие не изменится при увеличении высоты параллелепипеда и перестанет быть сквозным.
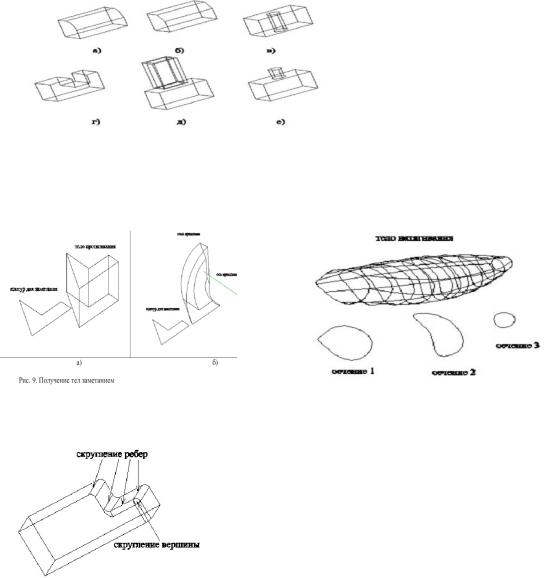
Рис.18
Функции параметрического моделирования создают тело перемещением параметрического плоского контура и накладыванием ограничений. Вращение или перемещение –sweeping, натягивание – skinning, поворот (вращение плоского контура) – swining, наложение ограничений и скругление поверхностей (фасок).
Функции заметания используют плоский замкнутый параметрический контур для получения модели тела. В этих функциях контур перемещается или вращается в пространстве чтобы сформировать тело. На рис. в одном случае получается тело протягивания, во втором - вращения.
Функция натягивания генерирует тело, создавая поверхность типа оболочки, заключающей некоторый объем для заданного набора сечений тела. Функции моделируют каркас тела очень близко к истинному каркасу, потому что базовые сечения описывают результирующее тело точно.
Функции сопряжения и скругления используются главным образом для модификации существующего каркаса тела.
- внесение изменений и перенос решений на новые платформы (технология синхронного моделирования).
До создания синхронной технологии существовали два основных способа 3D моделирования. Исторически первыми были системы с деревом построения. В них имеется графический интерфейс для отображения этот дерева, который допускает несложные манипуляции с ним. Между элементами дерева сохраняются взаимоотношения типа «родительпотомок». Размеры и взаимосвязи задаются, сохраняются и отслеживаются в дереве построений.
Второй способ - системы без дерева построения, или системы прямого моделирования, не использующие конструктивные элементы и практически не поддерживающие управление моделью при помощи размеров и геометрических взаимосвязей. Они базируются на B-Rep. Такие системы работают быстро и гибко, поскольку пересчет модели происходит только локально, в месте ее редактирования. Изменение предсказуемы и не требуют разработки стратегии. Синхронная технология является дальнейшим развитием технологии прямого моделирования, существующей как в Solid Edge, так и в NX сравнительно давно.
Технология текущих правил автоматически распознает взаимосвязи, такие как параллельность, касание, соосность, горизонтальность, вертикальность, и сохраняет их в процессе редактирования. Процедурные конструктивные элементы позволяют менять параметры отверстий, массивов, тонкостенных оболочек и скруглений в соответствии с концепцией поэлементного моделирования без наложения взаимосвязей между отдельными элементами модели.
Технология синхронного моделирования позволяет импортировать геометрию из других САПР, реализуя поэлементное моделирование без дерева построения и истории создания, задавая и синхронизируя параметры и правила проектирования в момент редактирования модели. Синхронная технология разработана на основе геометрического
ядра Parasolid, набора интегрированных модулей D-Cubed, использует пользовательский интерфейс в стиле Microsoft Office 2007, ленточное меню и воплощена в последних версиях продуктов Solid Edge, NX и CAM Express, анонсированных компанией Siemens PLM Software после 2008 г.
Визуализация используется как процесс представления данных для их более наглядного изображения и, в переносном значении, для описания психологических, литературных и др. процессов и понятий. Визуализации позволит рассмотреть модели зданий любым углом, увидеть множество движущихся людей и автомобилей, добавить растительность, световые блики, отражения в стёклах и полированных полах, показать реалистичные тени и воду. Наиболее распространена
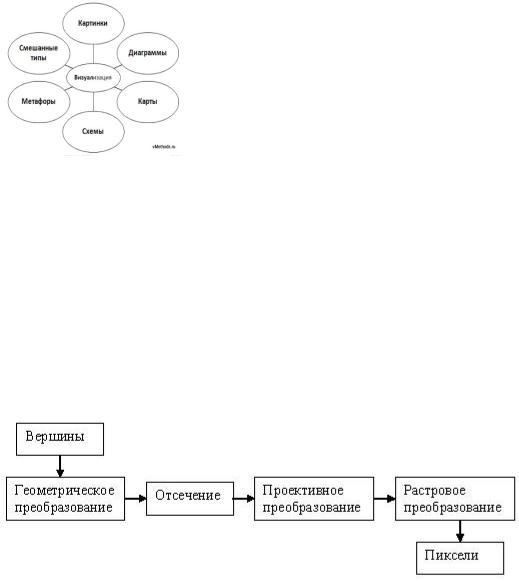
двумерная визуализация — изображение на плоскости и 3D - визуализация (на основе компьютерной техники и программного обеспечения - анимация, псевдостереоскопия).
Информация об изделии получается путем обработки пропускаемого, испускаемого или отраженного луча. Например, лучевой способ может быть основан на поглощении рентгеновских лучей, отражении ультразвуковых волн в направлении датчика, самопроизвольном испускании тканями инфракрасного излучения.
Созданный объект (процесс) можно «покрутить» в 3D вокруг своей оси, расположить удобнее для просмотра, выделить какую-либо деталь/часть/отсек и рассмотреть ее под нужным углом. При желании можно посмотреть любой разрез, цветом показать какое-либо из невидимых измерений (например, толщину), что упрощает и ускоряет процесс создания иллюстраций. 3D-визуализация может выявить, к примеру, нестыковку каких-либо деталей и другие ошибки, поэтому применяется предприятиями для сокращения расходов на проект. Например, система 3D-проектирования самолета Boeing 777 позволила разработчикам сэкономить 15% средств, затраченных на производство.
Большинство современных графических систем используют принцип конвейерной архитектуры. Построение некоторого изображения на экране монитора происходит поточечно, причем каждая точка проходит некоторый фиксированный цикл обработки. Сначала первая точка проходит первый этап этого цикла, затем переходит на второй этап, в это время вторая точка начинает прохождение первого этапа обработки и так далее, любая графическая система параллельно обрабатывает множество точек формируемого изображения. Такой подход позволяет существенно уменьшить время обработки всего изображения в целом, причем, чем сложнее изображение, тем больше получается выигрыш во времени. Конвейерная архитектура применяется для графических систем как на программном, так и на аппаратном уровне. На вход такого конвейера попадают координаты физической точки реального мира, а на выходе получаются координаты точки в системе координат экрана и ее цвет. В рассмотренном цикле обработки точки можно выделить несколько этапов, основными из них являются следующие:
1.Геометрические преобразования. На этапе геометрических преобразований координаты всех объектов реального мира приводятся к единой системе координат (мировая система координат). В компьютерной графике нередко используются приемы, с помощью которых сложные объекты представляются как совокупность простых (базовых) объектов, при этом каждый из базовых объектов может быть подвергнут некоторым геометрическим преобразованиям.
2.Отсечение. На этапе отсечения определяется, какие из точек попадут в поле зрения наблюдателя, и из этого множества
выбираются те, которые останутся видимыми. На этом этапе применяются алгоритмы удаления невидимых ребер и поверхностей.
3.Проецирование. На этапе проецирования координаты точки (до сих пор остающиеся трехмерными) преобразуются в координаты экрана с помощью преобразования проецирования.
4.Закрашивание. На этапе закрашивания осуществляется расчет цвета отображаемой точки с помощью методов локального или глобального закрашивания. Как правило, на этом этапе не удается использовать информацию об освещении всей сцены в целом, поэтому строятся модели освещенности различной степени детальности, которая во многом зависит от необходимости построения статического или динамического изображения.
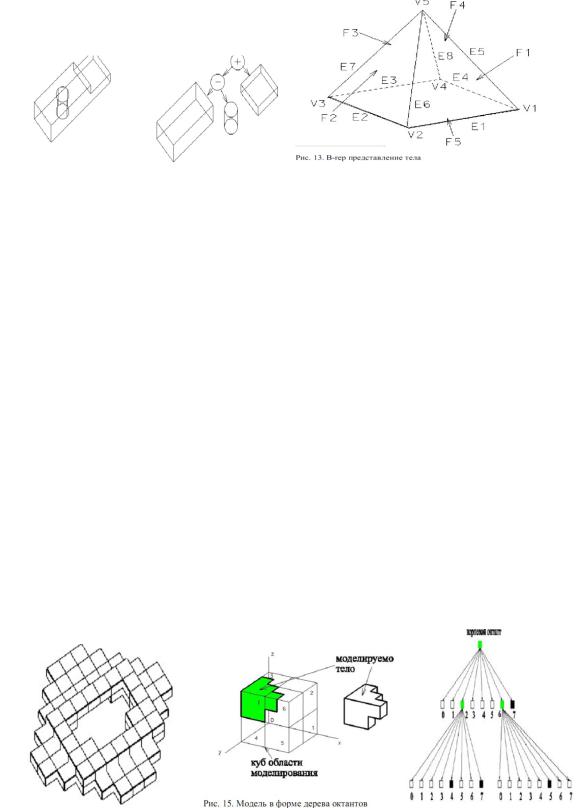
Рассмотрим структуры данных в различных форматах для однозначного математического описания тел. Можно выделить три основных структуры данных для твердотельного моделирования:
1. Представление конструктивной объемной геометрии (constructive solid geometry -CSG). CSG представление сохраняет в некотором графе хронологию применения булевых операций на примитивах. Этот граф называют CSG
деревом.
CSG представление имеет следующие преимущества:
-Структура данных, управление данными, проста и компактна.
-Тело, сохраненное в CSG дереве, будет всегда правильным телом.
-CSG представление тела может всегда преобразовано в соответствующее B-rep представление. Таким образом, CSG представление может быть связано соответствующим интерфейсом с прикладными программами, написанными для B-Rep.
- Параметрическое моделирование может быть легко реализовано путем изменения параметров соответствующих примитивов.
Недостатки:
- Поскольку CSG древовидная структура сохраняет последовательность применения булевых операций, то только эти операции разрешены в процессе моделирования, поэтому диапазон форм, которые будут смоделированы, строго ограничен. Кроме того, функции модификации типа сопряжения нельзя использовать.
- Требуется выполнить большой объем вычислений, чтобы из CSG дерева получить
информацию относительно граней, ребер и вершин и обеспечения связи между этими граничными объектами.
2.Граничное представление (boundary representation, B-Rep ) сохраняет граничную информацию для тела (вершины, ребра и грани вместе с информацией относительно того, как они связаны между собой). Эту структуру данных называют B- Rep структурой данных. Последовательность ребер для каждой грани определяется против часовой стрелки, когда тело рассматривается с его внешней стороны. Это правило позволяет иметь информацию о том, где находится внутренняя и внешняя часть тела, т.е. можно для любой точки определить, расположена ли она на внутренней или внешней части тела.
3.Декомпозиционная модель (decomposition model) сохраняет тело как агрегат из простых тел типа параллелепипедов. Можно выделить три типа таких моделей:
-Вокселные модели;
-Модели в форме дерева октантов (octree);
-Ячеечные модели.
Вокселная модель – это трехмерное расширение растрового представления двумерных форм (воксел - трехмерный аналог пиксела: pixel - picture element, voxel - volume element). Сначала создается квадрат области моделирования. Затем эта область разделяется на много маленьких квадратов линиями координатной сетки. Выбор интервалов между линиями координатной сетки зависит от желаемой точности представления. Квадрат области моделирования, содержащий много маленьких квадратов, представляется в компьютере двумерным массивом. Элементы массива, соответствующие маленьким квадратам, перекрывающим моделируемые объекты, имеют значение 1, а остающиеся элементы имеют значение 0. Таким образом, массив из 1 и 0 является растровым представлением двумерного объекта.
Представление трехмерного тела основано на такой же процедуре, как и растровое представление. Большой куб области моделирования разделяется на маленькие кубы, называемые вокселами, с помощью объемной сетки с равным шагом по осям x, y и z. Этот куб представляется в компьютере трехмерным массивом, каждый элемент которого имеет значение 1 или 0, в зависимости от позиции воксела в моделируемом теле. Хотя процесс получения вокселной модели почти такой же, как процесс растеризации, обнаружение перекрытия между телом и вокселом требует более сложных вычислений, чем вычисления в процессе растеризации.
Вокселные модели имеют следующие преимущества:
-Тело произвольной формы может всегда можно описать достаточно точно. Например, модели человеческих костей в томографии обычно представляются вокселными моделями.
-Легко вычислять массо-инерционные параметры тел простым суммированием соответствующих параметров вокселов.
-На таких моделях очень просто выполнять булевы операции.
-Легко моделировать препятствия при движении роботов.
Однако вокселные модели имеют и недостатки: - Требования к затратам памяти резко увеличивается при повышении точности моделирования. - Вокселные модели принципиально являются только приближенными.
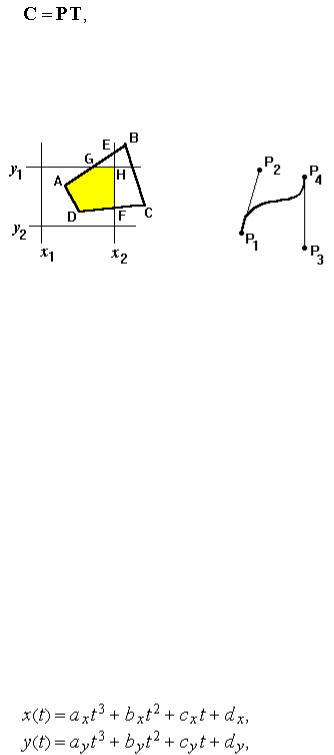
Рис. Дерево октантов -Модели в форме дерева октантов представляют тело как множество кубов, но при этом требования к затратам памяти
меньше, так как область моделирования делится на кубы по другому, чем для вокселных моделей. В вокселных моделях область моделирования разделяется на одинаковые по размерам кубы, независимо от представляемого тела. В моделях в форме дерева октантов, исходный куб области моделирования разделяется на восемь одинаковых кубов, которые в дальнейшем также делятся на восемь одинаковых кубов, соответственно, как показано на рис. 15.
Каждый куб - это одна восьмая по размерам от его родительского куба и поэтому он называется октантом. В свою очередь все октанты могут быть представлены как узлы дерева, в котором каждый узел имеет восемь ветвей.
Процедура получения модели в форме октантов следующая. Сначала создается исходный куб области моделирования, который полностью содержит тело, которое будет моделироваться. Этот куб называется корневым октантом. Затем
корневой октант разделяется на восемь октантов и рассматривается взаимное пространственное отношение каждого октанта относительно моделируемого тела. Если октант расположен полностью в теле, то он отмечается как "черный" (рис. 16.). Если он расположен полностью вне тела, он отмечается как "белый" (рис. 16.). Если он расположен частично внутри и частично снаружи тела, то он отмечается как "серый" (рис. 16.) и только такой октант разделяется в дальнейшем на восемь дочерних октантов. Октанты, отмеченные как черные или белые, далее не разделяются.
Этот шаг рекурсивно повторяется до тех пор, пока не останется более серых октантов. Множество черных октантов в полученном дереве и будут моделировать тело. Рис. 16. иллюстрирует дерево октантов, сгенерированное для тела, показанного на рис. 15. Число октантов, которые будут храниться в памяти, намного меньше, чем число вокселов в вокселных моделях, т.к. октанты отмеченные как черные или белые не участвуют далее в разделениях.
Ячеечные модели представляют тело как множество простых ячеек, как и в вокселных моделях. Однако в этих моделях не накладывается строгое ограничение на допустимую форму ячеек, которые используются. В результате любое тело может быть представлено только небольшим количеством простых ячеек. Разделение тела на множество конечных элементов (МКЭ) при анализе тел на прочность является типичным примером ячеечного моделирования.
CATIA (Computer Aided Three-dimensional Interactive Application) – это система
автоматизированного проектирования для машиностроения. Она основана на использовании параметризованных макроэлементов (features) при созданияи твердотельных параметрических моделей.
CATIA V5 разработана для среды Windows, и ведет себя тем же самым способом, как и другие приложения Windows. Традиционные выпадающие меню обеспечивают доступ ко всем командам CATIA. Интерфейс управляется прежде всего мышью с тремя кнопками. Чтобы выполнять работу в пределах документа CATIA, требуется использовать одну из инструментальных сред:
Part Design (конструктор детали): создает детали, используя подход твердотельного моделирования.
Sketcher (конструктор параметризованного эскиза): создает профили 2D со связанными ограничениями, которые используется для создания геометрии 3D.
Wireframe & Surface (каркас и поверхность): создает сложные параметризованные макроэлементы детали с каркасом 3D и поверхностными элементами.
Assembly Design (конструктор сборок): создает ограничения, параметризованные макроэлементы и спецификации для деталей в контексте сборки.
Drafting (интерактивное черчение): создает чертежи из проектов сборки и деталей.
CATIA графически отображает структуру детали и другие неграфические данные модели в дереве спецификации, которое показывает последовательность, в которой были созданы параметризованные макроэлементы и позволяет легко получить всю основную информацию о модели детали.
Меню и инструментальные панели
Инструментальные панели обеспечивают быстрый доступ к инструментальным средствам, которые являются так же доступными в меню.
1.Щелкнуть View (Вид) > Toolbars (Инструментальные панели).
2.Полный список инструментальных панелей будет показан вместе с текущей
3.Щелкнуть соответствующую инструментальную панель, чтобы активировать
или деактивировать эту инструментальную панель.
CATIA управляет инструментами через свертывание инструментальных панелей или стыковку дополнительных инструментальных панелей на границах экрана. Если не можете найти нужную, то проверьте, что:
A.Инструмент, который нужен, не расположен как выпадающий дополнительный инструмент.
B.Инструмент/инструментальная панель не расположен вне экрана. Ищите символы >> на границах экрана.
Инструментальная среда Sketcher (Конструктор параметризованного эскиза) – это среда, облегчающая создание эскизов 2D. Элементы, созданные в пределах конструктора параметризованного эскиза – это исключительно элементы 2D.
В инструментальной среде Part Design (конструктор детали) геометрические элементы, созданные в конструкторе параметризованного эскиза, используется для создания параметризованных макроэлементов 3D изменением положения контура в пространстве и наложением ограничений. Параметризованный эскиз создается так, чтобы его можно было быстро изменить, просто изменяя размеры. Содержит:
A.Сетка, которая помогает создавать эскизы.
B.Инструментальная панель Profile (Профиль), которая используется для создания
геометрии. Например, геометрия параметризованного эскиза создается с использованием инструментальных средств, доступных в инструментальной панели Profile (Профиль):
A. User-Defined Profile (Определенный пользователем эскиз)
B. Pre-defined Profiles, (Предопределенные эскизы) C. Circles (Круги),D. Splines (Сплайны) E. Ellipses and Parabolas
(Эллипсы и параболы) F. Lines (Линии). G. Axes (Оси) H. Points (Точки).
С. Инструментальная панель Constraint (Ограничения), которая используется для простановки размеров и наложения ограничений на эскиз.
D. Инструментальная панель Tools Sketch (Параметризованный эскиз), которая является плавающей инструментальной панелью, показывающей опции, доступные в течение создания геометрии.
Е. Инструментальная панель Operation (Операция) используется для изменения существующей геометрии параметризованного эскиза.
Параметризованные макроэлементы могут быть классифицированы как основанные на эскизе или как предопределенные элементы отделки деталей:
•основанные на эскизе 2D. В общем случае эскиз преобразуется в тело 3D вытягиванием, вращением, заметанием или разверткой.
•предопределенные - которые создаются непосредственно на твердотельной модели. Скругления и фаски – это примеры этого типа параметризованных макроэлементов.
-Управляющие размеры – это размеры, используемые при создании параметризованного макроэлемента. Они включают размеры, связанные с геометрией эскиза и с параметризованным макроэлементом непосредственно. Например, цилиндрический элемент вытягивания. Диаметром элемента вытягивания управляет диаметр параметризованного эскиза круга, а высотой элемента вытягивания управляет глубина, с которой вытягивается круг.
-Управляющие (геометрические) ограничения (типа параллельности, перпендикулярности, горизонтальности, вертикальности, концентричности и совпадения) устанавливают отношения положения элементов эскиза друг относительно друга.
-Уравнения (устанавливают математические отношения между параметрами). При использовании ограничений и уравнений можно гарантировать, что понятия проектирования типа сквозное отверстие или равные радиусы будут всегда выполняться.
Новые термины:
Features: (параметризованный макроэлемент). Как сборка (assembly) составлена из множества индивидуальных деталей (parts), так и детали в CATIA составлены из индивидуальных параметризованных макроэлементов (features). Геометрические элементы типа элементов вытягивания- (pad), карманов- (hole), отверстий -(fillet), скруглений, ребер, фасок (chamfer), желобков (lofting) и т.д. применяются для получения детали.
Parametric Sketch (параметрический эскиз). Размеры и отношения, которые создают параметризованный макроэлемент и сохраняются в модели.
Constraint (ограничения). Геометрические отношения, типа параллельности, перпендикулярности, горизонтальности, вертикальности, концентричности и совпадения или уравнений, которые устанавливают математические отношения для параметров.
Design Intent (план проектирования детали). План, который объясняет, как разрабатываетcя твердотельная модель детали, чтобы должным образом передать визуальные и функциональные аспекты детали.
Начало работы:
Впределах среды Windows, можно начать приложение несколькими путями:
A.Щелкнуть CATIA в меню Start (Пуск)> Mecanical DesignPart DesignSketcher.
B.File – New -Part
С. Дважды щелкнуть левой кнопкой мыши на существующем документе CATIA.
---------------------------------------------------------------------------------------------
В зависимости от способа формирования изображений компьютерную графику принято подразделять на растровую, векторную и фрактальную. Отдельным предметом считается трехмерная (3D) графика, изучающая приемы и методы построения объемных моделей объектов в виртуальном пространстве. Как правило, в ней сочетаются векторный и растровый способы формирования изображений.
Фрактальная графика основана на математических формулах, то есть никаких объектов в памяти компьютера не хранится и изображение строится исключительно по уравнениям. Таким способом строят как простейшие регулярные структуры, так и сложные иллюстрации, имитирующие природные ландшафты и трехмерные объекты.
Растр - точечная (в виде совокупности точек) структура графического изображения при полиграфической и цифровой печати. Основой растрового представления графики является пиксел с указанием его цвета. Цифровое изображение — это совокупность пикселей. Каждый пиксел растрового изображения характеризуется координатами x и y и тремя яркостями: красного, синего и зеленого цветов (VR, VB, VG)(x,y). Комбинируя данные три цвета можно получить большое количество различных оттенков. Цвет любого пиксела растрового изображения запоминается с помощью комбинации битов. Чем больше битов для этого используется, тем больше оттенков цветов можно получить. Под градацию яркости обычно отводится 1 байт (256 градаций), причем 0 — черный цвет, а 255 — белый (максимальная интенсивность). Для цветного изображения отводится по байту на градации яркостей каждого из трех цветов (человеческий глаз способен различать только 8 бит градаций на каждый цвет, хотя специальная аппаратура может потребовать и более точную передачу цветов).
Представление графических элементов в растровой форме требуется для отображения этих элементов на битовую карту растровой видеосистемы.
При редактировании растровой графики редактируются пиксели, а не линии. Растровая графика зависит от разрешения, поскольку информация, описывающая изображение, прикреплена к сетке определенного размера. Чем качественнее изображение, тем больше размер файла.
Растровое представление обычно используют для изображений фотографического типа с большим количеством деталей или оттенков. Масштабирование таких картинок в любую сторону обычно ухудшает качество. При уменьшении количества точек теряются мелкие детали и деформируются надписи. Добавление пикселей приводит к ухудшению резкости и яркости изображения, т.к. новым точкам приходится давать оттенки, средние между двумя и более граничащими цветами.
Растровое изображение ближе к фотографии, оно позволяет более точно воспроизводить основные характеристики фотографии: освещенность, прозрачность и глубину резкости. Распространены форматы .tif, .gif, .jpg, .png, .bmp, .pcx и др. Размер файла растровой графики сильно зависит от формата выбранного для хранения изображения. При прочих равных условиях существенное значение имеет схема сжатия изображения. Например, BMP файл имеет, как правило, большие размеры, по сравнению с файлами PCX и GIF, которые в свою очередь больше JPEG файла.
Растровая форма описывается тремя параметрами: пространственной частотой (плотность растра), характеристикой точки – формой, углом поворота (набор углов, под которыми располагаются друг к другу линии из точек растра) и линеатурой ( количество линий растра на длину). Каждый из этих факторов по-своему влияет на качество отпечатанного изображения.
В векторной графике базовым элементом изображения является линия, которая обладает формой (прямая, кривая), толщиной, цветом, начертанием (сплошная, пунктирная). Замкнутые линии приобретают свойство заполнения (текстурой, цветом). Линия может быть ограничена двумя точками, именуемыми узлами, все прочие объекты векторной графики составляются из линий. Векторный метод - это метод представления изображения в виде совокупности геометрических примитивов - отрезков и дуг, кубиков, шаров и т. д. Рисунок хранится как набор координат, векторов и других чисел, характеризующих набор примитивов. Например, куб можно составить из шести связанных прямоугольников, каждый из которых образован четырьмя связанными линиями. Линия описывается математически как единый объект, и потому объем данных для отображения объекта средствами векторной графики существенно меньше, чем в растровой графике. Трехмерная графика по сути является векторной. Изображение хранится в памяти компьютера в виде описаний составляющих его объектов. Чтобы объект был трехмерен, его поверхность предварительно строится как каркасная конструкция, состоящая из пространственных узловых точек, задаваемых тремя координатами (х, у, z), и ребер, соединяющих узлы. Далее поверхности назначается обтягивающий ее материал, описание свойств которого, помимо цвета и фактуры, включает особенности отражения, рассеивания, преломления и поглощения света.
Объект помещается в трехмерную сцену, которая может включать задний план (чаще всего растровое изображение), источники освещения, параметры атмосферы (например, дымка или туман), расположение камеры и характеристики ее объектива. Именно через камеру мы и наблюдаем трехмерную сцену. При ее визуализации для каждой точки поверхности
объекта рассчитывается: видна ли она из точки наблюдения, в которой расположена камера, или перекрывается другими объектами; как на нее падает свет от всех источников, как он отражается, преломляется, рассеивается, поглощается и какая часть отраженного света попадает в объектив камеры. На основе просчета всех точек, составляющих трехмерную сцену (этот процесс называется «рендеринг»), строится двухмерная растровая картинка, которую в данный момент и видит наблюдатель. При перемещении объекта или точки наблюдения весь расчет повторяется, строится новая двухмерная растровая картинка, а наблюдатель может видеть как бы трехмерную сцену в новом ракурсе.
К методам компьютерной графики относят методы построения и преобразования графических объектов (геометрия и способы преобразования точек, линий и примитивов), представления (развертки) линий в растровой форме, выделения окна, удаления скрытых линий, проецирования, закраски изображений.
В компьютерной графике используется три вида матриц: -матрица поворота, матрица сдвига, матрица масштабирования.
Перенос точки из положения 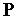 в новое положение
в новое положение  можно выполнять по формулам типа
можно выполнять по формулам типа
 где
где 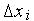 — приращение по координате
— приращение по координате 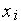 . Однако удобнее операции преобразования представлять в единой матричной форме
. Однако удобнее операции преобразования представлять в единой матричной форме
(1)
где 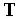 — преобразующая матрица. Выражение для сдвига с одновременным поворотом имеет вид
— преобразующая матрица. Выражение для сдвига с одновременным поворотом имеет вид 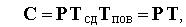 где
где 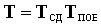 ,
, 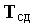 — матрица сдвига,
— матрица сдвига, 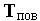 — матрица поворота.
— матрица поворота.
Выделение окна требуется при определении той части сцены, которая должна быть выведена на экран дисплея. После выделения экрана происходит наложение координатной сетки.
рис. кривая Безье Применяют ряд алгоритмов удаления скрытых линий . Один из наиболее просто реализуемых алгоритмов —
алгоритм z-буфера, где z-буфер — область памяти, число ячеек в которой равно числу пикселов в окне вывода.
Обычный буфер кадра хранит коды цвета для каждого пиксела в пространстве изображения. Идея состоит в том, чтобы для каждого пиксела дополнительно хранить еще и координату Z или глубину. При занесении очередного пиксела в буфер кадра значение его Z-координаты сравнивается с Z-координатой пиксела, который уже находится в буфере. Если Z- координата нового пиксела меньше, чем координата старого, т.е. он ближе к наблюдателю, то атрибуты нового пиксела и его Z-координата заносятся в буфер, если нет, то ничего не делается. В итоге z-буфер будет содержать пикселы наиболее близких к наблюдателю граней.
Предполагается, что ось 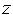 направлена по нормали к видовой поверхности и наблюдатель расположен в точке Z=0. В
направлена по нормали к видовой поверхности и наблюдатель расположен в точке Z=0. В
начале исполнения алгоритма все пикселы соответствуют максимальному значению 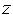 , т.е. максимальному удалению от наблюдателя, что приводит к помещению во все ячейки z-буфера значений пикселов фона картины (чертежа). Далее
, т.е. максимальному удалению от наблюдателя, что приводит к помещению во все ячейки z-буфера значений пикселов фона картины (чертежа). Далее
поочередно для всех точек граней рассчитываются значения координаты 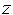 . Среди точек, относящихся к одному и тому же пикселу (одной и той же ячейке z-буфера S), выбирается точка с наименьшим значением Z и ее код (т.е. цвет и яркость) помещается в S.
. Среди точек, относящихся к одному и тому же пикселу (одной и той же ячейке z-буфера S), выбирается точка с наименьшим значением Z и ее код (т.е. цвет и яркость) помещается в S.
Моделирование эффектов отражения света от поверхности объекта в геометрических моделях называют рендерингом. Закраска матовых поверхностей основана на законе Ламберта, согласно которому яркость
отраженного от поверхности света пропорциональна 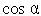 , где
, где 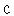 — угол между нормалью к поверхности и направлением луча падающего света. В алгоритме Гуро яркость внутренних точек рассматриваемой поверхности определяется линейной интерполяцией яркости в вершинах многоугольника. При этом сначала проводится интерполяция в точках ребер, а затем по строкам горизонтальной развертки. Более реалистичными получаются изображения в алгоритме Фонга, основанном на линейной интерполяции векторов - нормалей к поверхности.
— угол между нормалью к поверхности и направлением луча падающего света. В алгоритме Гуро яркость внутренних точек рассматриваемой поверхности определяется линейной интерполяцией яркости в вершинах многоугольника. При этом сначала проводится интерполяция в точках ребер, а затем по строкам горизонтальной развертки. Более реалистичными получаются изображения в алгоритме Фонга, основанном на линейной интерполяции векторов - нормалей к поверхности.
Важной составной частью геометрических моделей является описание поверхностей. Если поверхности детали — плоские грани, то модель может быть выражена достаточно просто определенной информацией о гранях, ребрах, вершинах детали методом конструктивной геометрии или полигональными сетками, если эти поверхности можно аппроксимировать множествами плоских участков. Чтобы построить по заданным координатам точек соединяющую их линию применяются методы интерполяции, вместо ломанной строят плавную кривую, заданную аналитически по методу кубических сплайнов, параболической интерполяции, использованию кривых Безье.
Аппроксимация полигональными сетками при больших размерах ячеек сетки дает заметные искажения формы, а при малых размерах ячеек оказывается неэффективной по вычислительным затратам. Поэтому более популярны описания неплоских поверхностей кубическими уравнениями в форме Безье или B-сплайнов. Знакомство с этими формами удобно выполнить, показав их применение для описания геометрических объектов первого уровня — пространственных кривых. В подсистемах графики и геометрического моделирования используются параметрически задаваемые кубические кривые
(1)
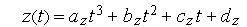
где 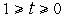 .
.
Применение кубических кривых обеспечивает выполнение четырех условий сопряжения сегментов соответствующим выбором четырех коэффициентов в каждом из трех уравнений. Применение полиномов выше третьей степени не рекомендуется, так как велика вероятность появления "волнистости".
Вслучае модели Безье этими условиями являются прохождение кривой сегмента через две заданные концевые точки
иравенство в этих точках касательных векторов соседних сегментов. В случае B-сплайнов выполняются условия непрерывности касательного вектора и кривизны (т.е. первой и второй производных) в концевых точках сегментов. Использование сплайнов обеспечивает высокую степень "гладкости" кривой, хотя прохождение аппроксимирующей кривой через заданные точки здесь не обеспечивается.
Кривы́е Бернште́йна-Безье́были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей.
Программы компьютерной графики
Графические редакторы предназначены для создания, сохранения и воспроизведения графических изображений.
Различают редакторы растровые и векторные.
Растровые графические редакторы выполняют такие функции, как воспроизведение сложных изображений типа фотографий, их редактирование с помощью операций закрашивания, обрезания, маскирования, изменения параметров всего изображения или его участков. В этом классе графических редакторов лидирующее положение занимает Adobe Photoshop. При его использовании все изображение строится из набора отдельных слоев-картинок, имеющих прозрачные и закрашенные участки. Можно создавать, удалять, копировать, комбинировать участки, регулировать прозрачность и порядок расположения слоев. В пакете предусмотрены возможности построения и редактирования также векторных изображений.
Векторные редакторы позволяют создавать изображения типа схем, чертежей, диаграмм, простых рисунков. Одним из наиболее известных векторных редакторов является Corel Draw. Характерные возможности этого редактора — привязка линий к определенной позиции на изображении, создание выносок и размерных линий, работа с многостраничными изображениями, стандартный интерфейс Windows, многоуровневый откат, кроссплатформенность (имеются версии для Windows, OS/2, MAC, различных вариантов UNIX). Примеры других векторных редакторов — Microsoft Paint, iGrafx Designer, Visio 2000, Adobe Illustrator.
Для синтеза трехмерных изображений в САПР преимущественно используют средства таких известных систем, как CATIA, Unigraphics, Inventor, Solidworks и др. Однако кроме них существуют и применяются графические библиотеки и пакеты компьютерной графики и геометрического моделирования, непосредственно не связанные с проектированием в технике. К числу графических библиотек, получивших наибольшее распространение, относится библиотека графических процедур Open GL.
Open Graphics Library — открытая графическая библиотека и спецификация (стандарт) на интерфейсы программирования трехмерной графики. Библиотеку выпускают такие корпорации, как Microsoft, Silicon Graphics, а также просто группы программистов. В библиотеке OpenGL имеются процедуры построения графических примитивов (к
числу которых относят точки, линии, полигоны), удаления невидимых линий, Z-буферизации, реалистичной засветки,
задания положения тел и камеры наблюдения и т.п. Примитивы могут быть как векторными, так и растровыми. Важной особенностью технологии OpenGL является инвариантность к аппаратно-программным платформам. Единицей информации в OpenGL является вершина, из вершин формируются более сложные объекты. Программист создает вершины, указывает, как их соединять (линиями или многоугольниками), устанавливает координаты и параметры камеры и ламп, а библиотека Open GL берет на себя работу создания изображения на экране. С помощью Open GL создаются трехмерные поверхности, текстуры, моделируются источники света, создаются эффекты тумана, прозрачности, смешивания цветов, имеются операции анимации с передвижением объектов сцены.
Альтернативой OpenGL для платформы Microsoft является комплекс DirectX (Direct eXtension). Он представляет собой графический интерфейс прикладного программирования API ( Application Programming Interface) для решения задач, относящихся к мультимедийным приложениям, в частности, для разработки компьютерных игр. В DirectX входит несколько API, один из них Direct3D используется для 3D-графики, другие - для звука, музыки, устройств ввода и т.д.. До появления API каждый производитель графических процессоров использовал собственный механизм общения с приложением, и разработчикам приложений приходилось писать отдельный код для каждого графического процессора, который они хотели поддержать. Поэтому для каждого приложения указывалось, какие именно видеокарты оно поддерживает.
Чтобы решить проблему совместимости разных прикладных программ с видеокартами, был выполнена унификация интерфейсов - разработан специальный графический API. За 3D-графику в DirectX отвечает API Direct3D, и когда говорят о видеокартах, то имеют в виду именно его (поэтому понятия DirectX и Direct3D взаимозаменяемы). Последней выпущенной версией является DirectX 11.
Примеры функций в Direct3D: масштабирование, перемещение и вращение объектов, представленных матрицами; мировое преобразование (трансформации координат объектов, заданных в локальных системах, в мировую систему координат); проецирование (перспективное и ортогональное); инициализация и очистка z-буфера; переход в систему координат камеры и др.
Первый графический процессор с поддержкой API DirectX 10 — это NVIDIA GeForce 8800. Графический
процессор предназначен для хранения, обработки и передачи на монитор данных о выводимом на экран изображении. ГП существенно повышает производительность компьютера, освобождая центральный процессор (ЦП) от обработки графических данных. По своей сложности современные ГП могут превосходить ЦП.
Графические процессоры имеют конвейерную архитектуру. В классическом варианте различают вершинные и пиксельные процессоры — конвейеры. Поступающие в ГП данные об изображаемом объекте сначала обрабатываются в вершинном процессоре (Vertex Pipeline) с помощью программ, называемых вершинными шейдерами (Vertex Shader).
Шейдер - функция и программа компьютерной графики для создания тех или иных эффектов в изображениях. Виды шейдеров: вершинные, пиксельные, геометрические.
Вершинный шейдер рассчитывает геометрию сцены и параметры вершин (координаты, цвет, освещение и др.), может выполнять такие операции, как деформация и анимация, модификации, трансформация и уничтожение 3Dобъектов. Далее происходит сборка (Setup) трехмерной модели в полигоны. На этом этапе вершины соединяются между собой линиями, образуя каркасную модель. При соединении вершин друг с другом образуются полигоны (треугольники).
После этапа сборки данные поступают в пиксельный процессор, который определяет конечные пикселы, их цвета, которые будут выведены в кадровый буфер. Пиксельный процессор работает под управлением пиксельных шейдеров. Пиксельный процессор в итоге своей работы выдает конечное значение цвета пиксела и Z-значение для последующего этапа конвейера. При обработке графической информации возможны ситуации, когда заняты все вершинные процессоры и лишь часть пиксельных процессоров, остальные пиксельные процессоры простаивают. Поэтому,
компания NVIDIA предложила применять и разработала унифицированные графические процессоры, которые могли бы выполнять как вершинные, так и пиксельные шейдеры.
Унифицированные процессоры NVIDIA GeForce 8800 могут выполнять также обычные расчеты, чего вообще не было предусмотрено в графических процессорах предыдущих поколений. Унифицированные процессоры NVIDIA называются
унифицированными потоковыми процессорами (Unified Streaming Processors, SP) и представляют собой скалярные процессоры общего назначения для обработки данных с плавающей запятой. Процессор распределения задач способен распараллеливать шейдерный код на сотни потоков (до 512 потоков), увеличивая эффективность выполнения вершинных и пиксельных операций.
Cемейство GeForce 8800 обладает мощной параллельной архитектурой унифицированных шейдеров и состоит из 128 обособленных, совершенно самостоятельных потоковых процессоров с тактовой частотой до 1,35 ГГц. Каждый конвейерпроцессор, в свою очередь, способен динамически переназначаться для обработки вершинных, пиксельных, геометрических или физических операций, обеспечивая таким образом пиковую загрузку ресурсов GPU и максимальную сбалансированную гибкость при обработке шейдерных задач.
Мобильные профессиональные графические решения NVIDIA® Quadro® с 4ГБ видеопамяти и 384 ядрами CUDA - это технологический прорыв, построенный на инновационной архитектуре NVIDIA Fermi. Новейшие мобильные графические решения Quadro обладают высокопроизводительными вычислительными возможностями с передовой визуализацией, которые превратят ваш ноутбук в мобильный суперкомпьютер.
Основанные на вычислительной архитектуре "Fermi", графические процессоры Tesla созданы для высокопроизводительных вычислений, обеспечивают прирост производительности приложений до 10 раз и являются идеальным решением для обработки сейсмических данных, моделирования в биохимии, моделирования погоды и климата, обработки сигналов, вычислений в области финансов, CAE, CFD и анализа данных.
Успехи компании NVIDIA в производстве ГП более 10 лет назад привели к обладанию большим количеством инноваций, продвижению на мировом рынке ее собственной платформы для портативных устройств NVIDIA Tegra, а также мобильных видеокарт, которые действительно востребованы на мировом рынке – производители выставки 2011 представили бессчетное множество планшетников, и подавляющее большинство из них базируется именно на NVIDIA Tegra 2. NVIDIA Tegra — процессор, объединяющий функции целого компьютера в одном чипе (система на кристалле, SoC — System-on-Chip), разработанный компанией NVIDIA как платформа для производства мобильных устройств, таких
как смартфоны, смартбуки, КПК и тд. Кристалл Tegra объединяет в себе ARM-процессор, графический процессор, медиа- и DSPпроцессоры, контроллеры памяти и периферийных устройств, имея при этом низкое энергопотребление. Первый в мире мобильный суперчип NVIDIA® Tegra™ 2 обеспечивает экстремальные возможности мультизадачности с первым мобильным двухядерным CPU и лучшие сетевые возможности: просмотр интернет-страниц вдвое быстрее, аппаратноускоренный флеш и игры консольного качества с GPU NVIDIA® GeForce®. NVIDIA GPU становятся основой всей линейки продуктов MacBook, а также iMac, Mac Mini, Mac Pro и Apple TV решений.
Альтернатива - AMD (Radeon HD 6570 и Radeon HD 6670).
Лекция 6. Математическое обеспечение (МО) анализа проектных решений
К МО относят алгоритмы выполнения проектных процедур, математические модели и методы их решения. Компоненты МО определяются базовым математическим аппаратом, специфичным для каждого из иерархических уровней проектирования.
На микроуровне типичные математические модели (ММ) представлены df уравнениями в частных производных с краевыми условиями. В качестве независимых переменных фигурируют пространственные переменные x,y,z и время t . К этим моделям, еще называемым распределенными, относятся многие уравнения математической физики. Объектом исследования являются поля физических величин, что требуется при анализе прочности и теплопроводности машиностроительных деталей, потоков частиц в электронных приборах, распространения радиоволн в волноводах и пространстве. Число совместно исследуемых различных сред, деталей, слоев, фаз агрегатного состояния невелико вследствии сложностей вычислительного характера.
Резко снизить вычислительные затраты можно, применив иной подход к моделированию, основанный на принятии определенных допущений, в частности, отказе от изменения параметров по осям координат. Такое допущение, основанное на дискретизации пространства, описывает модели макроуровня. Модели называются сосредоточенными и описываются системами алгебраических и обыкновенных df уравнений с независимой переменной - время t. Упрощение описания отдельных компонентов (деталей) позволяет исследовать модели процессов в устройствах, число компонентов в которых может доходить до тысяч.
Когда число компонентов в исследуемой системе превышает некоторый порог, сложность модели вновь становится чрезмерной. Поэтому переходят на функционально-логический уровень, используя аппарат передаточных функций для непрерывных процессов и аппарат математической логики и конечных автоматов для процессов с дискретным множеством состояний.(* Конечный автомат
начинает работу в состоянии q0, считывая по одному символу входной цепочки. Считанный символ переводит автомат в новое состояние в соответствии с функцией переходов. Читая входную цепочку x и делая один такт за другим, автомат оказывается в каком-то состоянии q').
Для исследования производственных предприятий и их объединений, вычислительных систем и сетей, социальных сетей, применяют аппарат теорий массового обслуживания и другие подходы. Эти модели относятся к системному уровню моделирования.
Требования к математическим моделям (ММ) и методам САПР.
Основными требованиями к математическим моделям являются требования адекватности, точности, экономичности.
Модель всегда лишь приближенно отражает некоторые свойства объекта. Адекватность - область в пространстве параметров, в пределах которой погрешности модели остаются в допустимых пределах. Например, область адекватности линеаризованной модели
поверхности детали определяется системой неравенств: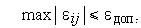 где допустимыми параметрами для радиоэлемента, например, могут быть внешнее напряжение, частоты, температуры. Под точностью понимают степень соответствия оценок одноименных свойств объекта и модели. Экономичность (вычислительная) определяется затратами ресурсов, требуемых для реализации модели. Поскольку в САПР используются математические модели, экономичность их будет характеризоваться затратами машинного времени и памяти, например, при выборе прямых или итерационных методов решения. Устойчивость определяется ростом ошибок при выполнении отдельных вычислительных операций. Неустойчивое решение является результатом неудачного
где допустимыми параметрами для радиоэлемента, например, могут быть внешнее напряжение, частоты, температуры. Под точностью понимают степень соответствия оценок одноименных свойств объекта и модели. Экономичность (вычислительная) определяется затратами ресурсов, требуемых для реализации модели. Поскольку в САПР используются математические модели, экономичность их будет характеризоваться затратами машинного времени и памяти, например, при выборе прямых или итерационных методов решения. Устойчивость определяется ростом ошибок при выполнении отдельных вычислительных операций. Неустойчивое решение является результатом неудачного
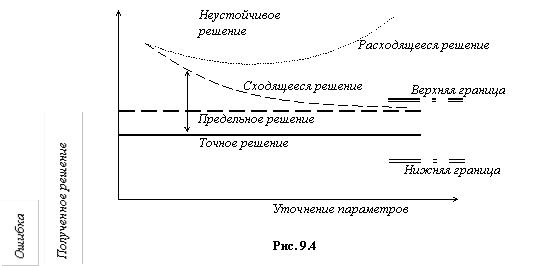
выбора аппроксимирующих функций, «плохой» разбивки области на КЭ, некорректного представления граничных условий и т. п. Под сходимостью подразумевается постепенное приближение последовательных решений к предельному, правильному.
Абсцисса обозначает степень уточнения параметров дискретной модели, а ордината определяет полученное при этом уточнении приближенное решение. На графике показан монотонный тип сходимости, при котором точность решения повышается плавно.
Модели микроуровня – в техническом аспекте это задачи математической физики, к которым относятся задачи теплопроводности, диффузии, электростатики и электродинамики, задачи о течении жидкости, распределении плотности электрического тока в проводящей среде, задачи о деформации твердых тел и многое другое. Система дифференциальных уравнений, как правило, известна (уравнения Ламе для механики упругих сред; уравнения Навье-Стокса для гидравлики; уравнения теплопроводности для термодинамики и т.д.), но точное решение удается получить лишь для частных случаев, поэтому первая задача, возникающая при моделировании, состоит в построении приближенной дискретной модели.
Для этого используются методы конечных разностей, метод конечных элементов и интегральных граничных уравнений, одним из вариантов последнего является метод граничных элементов. (Cущность методов интегральных граничных уравнений состоит в преобразовании дифференциальных уравнений в эквивалентную систему интегральных уравнений в качестве первого шага решения задачи. Такая операция, даст систему уравнений, включающую только значения переменных на границах области. Любая дискретизация будет приводить лишь к разбиениям поверхности, ограничивающим область.
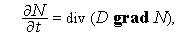
Пример 1 Уравнение теплопроводности:
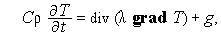 где
где  — удельная теплоемкость,
— удельная теплоемкость,  — плотность,
— плотность, 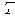 — температура,
— температура, 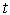 — время,
— время, 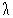 — коэффициент теплопроводности,
— коэффициент теплопроводности, 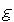 — количество теплоты, выделяемой в единицу времени в единице объема.
— количество теплоты, выделяемой в единицу времени в единице объема.
Пример 2 Уравнение диффузии:
где 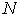 — концентрация частиц,
— концентрация частиц, 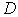 — коэффициент диффузии.
— коэффициент диффузии.
Пример 3 Уравнения непрерывности, используемые в физике полупроводниковых приборов: для дырок и электронов(с
заменой p на n) Здесь  и
и  — концентрации дырок и электронов;
— концентрации дырок и электронов; 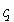 — заряд электрона;
— заряд электрона; 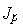 и
и 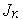 — плотности дырочного и электронного токов;
— плотности дырочного и электронного токов; 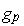 и
и 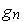 — скорости процессов генерации-рекомбинации дырок и электронов;
— скорости процессов генерации-рекомбинации дырок и электронов; 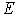 — напряженность
— напряженность
электрического поля; 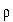 — плотность электрического заряда;
— плотность электрического заряда; 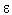 и
и 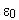 — диэлектрическая проницаемость и диэлектрическая постоянная.
— диэлектрическая проницаемость и диэлектрическая постоянная.
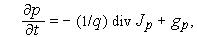 а также уравнение Пуассона:
а также уравнение Пуассона: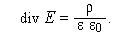
Заметим, приведенные уравнения «подозрительно» похожи – они описывают закон сохранения dФ/dt =-divJ +G, где Ф -фазовая переменная, J-поток фазовой переменной, G-скорость генерации субстанции.
Здесь divA =(d/dx+d/dy+d/dz)A, grad U(вектор) = (d/dx, d/dy, d/dz)U(x,y,z)
Пример 4. Волновое уравнение
При расчёте параметров устройств СВЧ геометрические размеры устройств становятся соизмеримы с длиной волны и все процессы, протекающие в устройствах, приобретают волновой характер. Для описания параметров можно не принимать во внимание внутреннюю структуру устройства, а ограничиться лишь внешними характеристиками. Тогда любое устройство СВЧ представляется в виде многополюсника, на каждый из входов которого поступает определенный тип волны, распространяющийся в линии. На каждом входе многополюсника существуют как падающая, так и отражённая волны. Отраженные волны b связаны с падающими a волнами линейными зависимостями.
, |
, |
здесь S – матрица рассеяния. |
Картина поля бегущей волны может быть определена, решая уравнения Максвелла. В многомерном случае однородное волновое уравнение записывается в виде
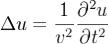 ,где
,где  — оператор Лапласа
— оператор Лапласа 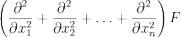 ,
,  — неизвестная функция,
— неизвестная функция, 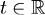 — время,
— время, 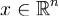
— пространственная переменная,  — фазовая скорость.
— фазовая скорость.
Следующее уравнение внутри волновода получено из уравнения Максвелла:
где: |
- градиент (направление наискорейшего возрастания) |
напряженности электрического поля E(x,y).
•E (x, y) - комплексная амплитуда, представляющая электрическое поле.
•ko - волновое число свободного пространства, 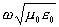 ,
,
•w - угловая частота, 2pif.
•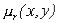 - комплексная относительная магнитная проницаемость.
- комплексная относительная магнитная проницаемость.
•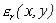 - комплексная относительная диэлектрическая проницаемость.
- комплексная относительная диэлектрическая проницаемость.
Решая это уравнение получаем картину поля для комплексной амплитуды E (x, y). Это решение независимо от z и t; и только после
умножения на  станет бегущими волнами.
станет бегущими волнами.
Вычисленная картина поля справедлива только для одной частоты. При генерации сигналом возбуждения одной конкретной моды поле будет содержать отраженные волны более высокого порядка, которые возникают из-за неоднородностей в СВЧ структуре. Если эти моды более высокого порядка отражаются назад к порту возбуждения или передаются на другой порт без особых потерь или без нераспространяемых типов волн, то могут быть рассчитаны S-параметры, связанные с этими модами. Если затухание типов волн более высокого порядка значительно, то нет никакой необходимости получать S-параметры для этой моды.
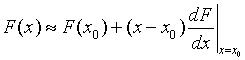
Аналитическое решении уравнений матфизики возможно лишь для ограниченного круга задач. В большинстве случаев решение df уравнений в частных производных состоит в дискретизации уравнений, т.е. представлении производных в виде приближенных выражений (конечных разностей), что позволяет преобразовать df уравнения в системы алгебраических уравнений. Иными словами, значения переменных исследуются для некоторого подмножества точек G области определения. Число алгебраических уравнений в полученной системе определяется произведением числа точек координатной сетки на количество независимых переменных в каждой точке (исходных df уравнениях). В нестационарных задачах вводится дополнительно сетка времени.
Дискретизация заключается в замене непрерывных переменных конечным множеством в заданном пространственном и временном интервалах. Алгебраизация – в замене производных алгебраическими выражениями. Линеаризация - разложение в ряд Тейлора в окрестности точки начального приближения к решению и пренебрежением всеми членами ряда кроме линейных.
Выбор метода решения полученной системы алгебраических уравнений определяется ее размерностью и характером (линейный или нелинейный). Для решения систем линейный алгебраических уравнений (СЛАУ) используют метод исключения Гаусса (метод последовательного исключения неизвестных из системы уравнений), метод LU-разложения. Для решения систем нелинейных алгебраических уравнений и линейных систем большой размерности используют итерационные методы Якоби, Зейделя, Ньютона-
Рафсона и др.
Краевые условия включают начальные условия, характеризующие пространственное распределение зависимых переменных в начальный момент времени, и граничные условия, задающие значения этих переменных на границах рассматриваемой области в функции времени. Различают ГУ первого рода (или условия Дирихле) U(x,t)=g(x,t)
и условия второго рода (Неймана)
dU(x,t)/dn= g(x,t) ,где п-вектор нормали к поверхности. ГУ третьего рода есть сочетание первых двух. Например, применительно к задаче теплопроводности, граничные условия первого
рода задают температуру на границе, а условия второго рода задают поток на границе.
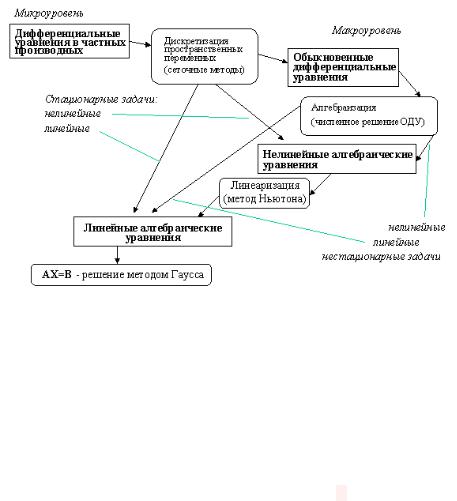
Рис. Преобразование математических моделей в процессе
моделирования.
МКР, МКЭ
Моделирование многочисленных физических, биологических и химических явлений часто приводит к решению линейных или нелинейных уравнений или систем уравнений в частных производных. Существуют традиционные математические средства, позволяющие получить решение в определенных случаях (анализ Фурье, разложение в ряд и т. п.), но для решения конкретных проблем, возникающих в науке и технике, невозможно обойтись без использования численных методов. Любое численное моделирование позволяет дополнить или даже заменить прямой эксперимент. Последний часто дорог, его постановка бывает трудоемкой или вообще невозможной (моделирование устойчивости плотин, землетрясения, исследование солнечных явлений).
Разработано много методов численного решения уравнений в частных производных. Наиболее часто используемые из них - методы конечных разностей и конечных элементов. Построение конечно-разностных схем обычно требует небольшого объема вычислений, как правило, меньшего, чем в МКЭ. Достоинствами МКЭ являются гибкость и разнообразие сеток, стандартные приемы построения дискретных задач для произвольных областей, простота учета естественных краевых условий и т. д. Методы КЭ применимы к более широкому классу исходных задач, оценки погрешностей приближенных решений получаются при менее жестких ограничениях, чем в методе конечных разностей.
Метод конечных разностей был разработан раньше остальных и, на первый взгляд, является наиболее простым в реализации. Истоки метода связаны с именами Непера (логарифмические таблицы Брадиса), Ньютона, Эйлера, Лапласа и Лагранжа. Слово «конечные» используется здесь в смысле - «не бесконечно малые», не связанные с предельными переходами.
Разности встречаются также в любой ситуации, когда надо описать поведение объекта, который испытывает воздействие меняющихся условий во времени и в пространстве. Например, термостату требуется значительное время, чтобы отреагировать на изменение температуры, поэтому он реагирует не на текущую температуру, а на ту, что была минуту назад.
Идея метода состоит в разбиении прямоугольной сеткой области, в которой решается уравнение, и дискретизация дифференциального оператора. Решая линейную систему уравнений, находят приближенные решения в узлах решетки. Основные трудности связаны с учетом граничных условий, если граница области имеет сложную геометрическую форму. Метод конечных разностей предполагает дискретизацию df уравнений на прямоугольных координатных сетках (для двух измерений).
Основные понятия теории разностных схем — понятия сходимости, аппроксимации и устойчивости. Сходимость разностной
схемы означает, что при достаточно малом шаге значения сеточного (приближенного) и точного решения мало отличаются. Аппроксимация на решение означает, что при подстановке точного решения дифференциальной задачи в разностную схему мы получаем невязку соответствующего порядка малости (идеально бы иметь нуль). Устойчивость означает, что малые возмущения в начальных данных и правой части разностной схемы приводят к равномерно малому изменению решения.
Производная df(x)/dx= lim (fx-f0)/(x-x0). Обычно x-xi = h(шаг). Тогда производная определяется в зависимости от нахождения соседних точек разбиения (так называемого шаблона). Замещение частных производных в уравнениях матфизики разностными выражениями позволяет получить приближенное решение системы алгебраических уравнений в узлах сетки.
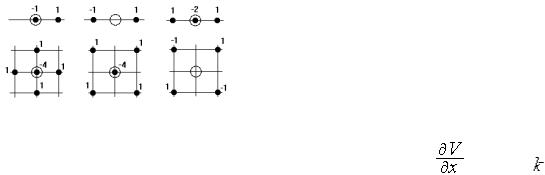
Рис. 1. Примеры шаблонов для одномерных и двумерных задач
На этом рисунке кружком большего диаметра обозначены узлы, в которых аппроксимируется производная. Для одномерных шаблонов в
верхней части рисунка показана аппроксимация производной |
в точке , и указанным шаблонам при их просмотре слева направо |
соответствуют аппроксимации |
|
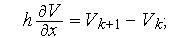
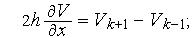 для равномерной сетки,
для равномерной сетки, 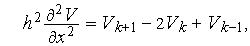 Аппроксимацию второй производной можно получить исходя из ее определения, — отношение приращения функции к приращению аргумента, где в качестве функции выступает аппроксимация первой производной.
Аппроксимацию второй производной можно получить исходя из ее определения, — отношение приращения функции к приращению аргумента, где в качестве функции выступает аппроксимация первой производной.
Выражения для конечных разностей можно получить из разложения функции в ряд Тейлора:
Или более коротко с использованием индексов точек:
(1)
Отсюда |
, где |
— остаток. |
Отбрасывая остаток, можно получить правую и, аналогично, левую разность: |
||
; |
|
Погрешность такой аппроксимации определяется старшим членом в отброшенном |
остатке и в данном случае этот член содержит 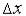 в первой степени.
в первой степени.
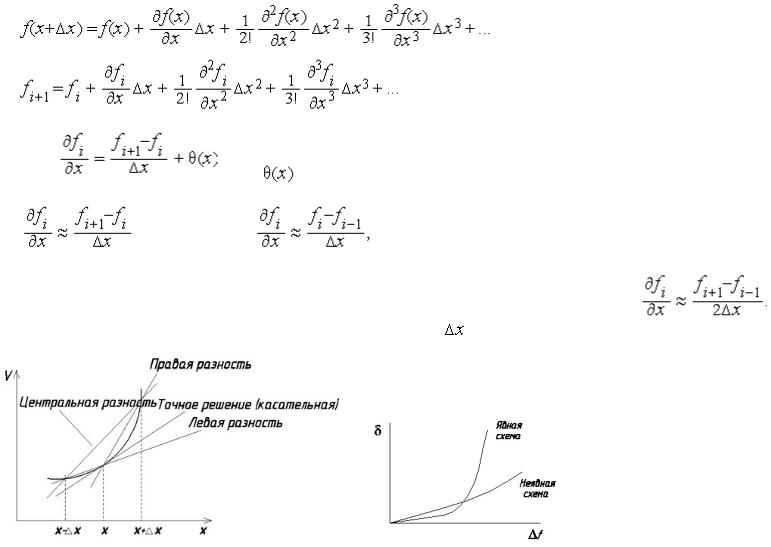
Более точная аппроксимацию первой производной называется центральной разностью: |
В этом случае член, |
|
определяющий погрешность аппроксимации, будет содержать |
во второй степени. |
|
Графическая интерпретация некоторых конечно-разностных аппроксимаций для производных. |
|
|
Существуют разностные схемы, которые позволяют повысить точность решения за счет более сложной аппроксимации производной, например dV/dt = (2Vn-3Vn-1+Vn-2)h – метод трапеций.
Формула явного метода Эйлера представляет собой следующую формулу замены производных в точке 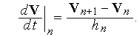 При применении явных методов происходит потеря устойчивости вычислений, а это означает, что в решении задачи возникают ложные колебания с увеличивающейся от шага к шагу амплитудой и быстрым аварийным остановом ЭВМ вследствие переполнения разрядной
При применении явных методов происходит потеря устойчивости вычислений, а это означает, что в решении задачи возникают ложные колебания с увеличивающейся от шага к шагу амплитудой и быстрым аварийным остановом ЭВМ вследствие переполнения разрядной
сетки. Конечно, ни о какой адекватности решения говорить не приходится. Неявные методы требуют малых шагов. 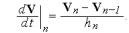
Среди неявных разностных методов устойчивы методы Эйлера, методы второго порядка (основаны на комбинированном использовании явной и неявной формул Эйлера) и среди них — метод трапеций.
Алгоритм решения стационарных краевых задач методом конечных разностей
Алгоритм решения задач МКР следующий:
-Нанесение на объект сетки или дискретизация пространства.
-Нумерация узлов сетки.
-Запись разностного уравнения для каждого внутреннего узла сетки.
-Запись уравнений граничных условий для приграничных узлов.
-Решение системы алгебраических уравнений
Идея метода конечных элементов
Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей (элементов). В каждом из элементов выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами и выражаются через значения функций в узлах. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, умноженному на число узлов и ограничивается только возможностями ЭВМ. Каждый из элементов связан с ограниченным количеством соседних, поэтому СЛАУ имеет разрежённый вид, что существенно упрощает её решение.
Идеализация сплошной среды заключается в замене ее системой пластинчатых элементов, шарнирно соединенных в узлах.
Выделенный элемент имеет те же физические свойства, что и рассматриваемая среда в месте расположения элемента. Идентификация напряженно-деформированного состояния сплошной среды и среды, разделенной на элементы, достигается выполнением условия непрерывности на границах между элементами.
Форма элементов может быть произвольной - треугольной, четырехугольной, прямоугольной. Наиболее простое решение получается при разделении среды на элементы треугольной формы. Сетка разбивки может содержать одновременно элементы разной формы и размеров. Расчет напряженно-деформированного состояния конструкции в рамках линейной теории упругости при действии на нее статических нагрузок сводится к решению системы линейных алгебраических уравнений (СЛАУ). В конечно-элементных комплексах программ используются разнообразные методы решения больших систем уравнений: в программах ADINA реализован
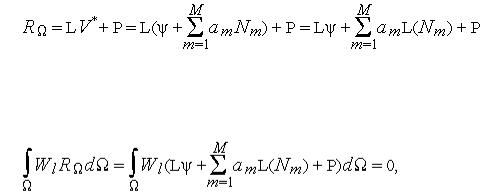
блочный метод Гаусса, в ASKS, SAP-7 - ленточный метод Гаусса, в NASTRAN - LТDL декомпозиция, в ANSYS фронтальный метод и разложение Холецкого.
Метод конечных элементов — универсальный метод решения систем дифференциальных уравнений в частных производных. По способу получения основных уравнений различают четыре основных вида метода конечных элементов: прямой, вариационный, взвешенных невязок и энергетического баланса.
Метод взвешенных невязок — универсальный метод нахождения коэффициентов в аппроксимациях. Применительно к решению систем дифференциальных уравнений в частных производных этот метод можно продемонстрировать следующим образом.
Пусть есть некоторый дифференциальный оператор 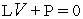 , описывает поведение некоторой сплошной среды
, описывает поведение некоторой сплошной среды 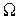 и заданы граничные условия первого рода
и заданы граничные условия первого рода 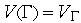 . Идея метода взвешенных невязок основана на подборе решения, но не
. Идея метода взвешенных невязок основана на подборе решения, но не
произвольным образом, а целенаправленно, в виде при этом функция
при этом функция 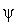 на границе точно удовлетворяет граничным условиям, а функции
на границе точно удовлетворяет граничным условиям, а функции 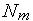 , которые называются пробными функциями, на границе принимают нулевое значение, т.е.
, которые называются пробными функциями, на границе принимают нулевое значение, т.е.  .
.
При подстановке  в (1) получим невязку
в (1) получим невязку
Потребуем, чтобы невязка 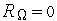 приближенно в любой точке
приближенно в любой точке 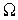 , например
, например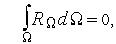 но в этом случае при
но в этом случае при  после
после
раскрытия интеграла придем к незамкнутой системе уравнений относительно 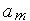 . Поскольку мы хотим, чтобы
. Поскольку мы хотим, чтобы 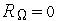 , то домножение невязки на некоторую фунцию не должно изменить значения интеграла, то есть
, то домножение невязки на некоторую фунцию не должно изменить значения интеграла, то есть
где 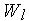 - функции, которые называются весовыми.
- функции, которые называются весовыми.
От выбора весовых функций зависит к какому конкретно варианту метода взвешенных невязок мы придем. Наиболее употребимыми являются метод поточечной коллокации, метод коллокаций по подобластям и метод Галеркина, в котором в качестве весовых
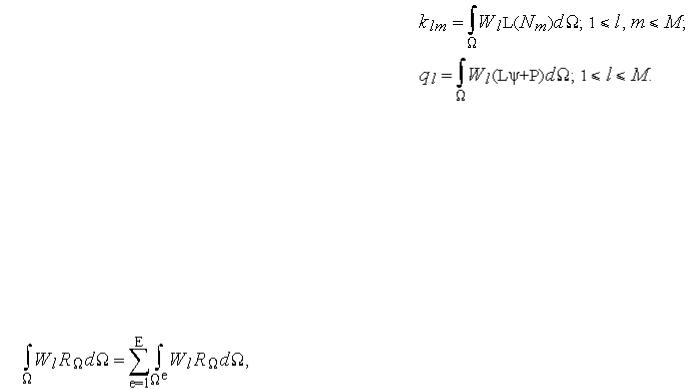
функций используются сами пробные функции  . Для решения нужно найти неизвестные коэффициенты аm из системы
. Для решения нужно найти неизвестные коэффициенты аm из системы
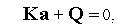 разведя коэффициенты при пробных функциях и свободных членах.
разведя коэффициенты при пробных функциях и свободных членах.
Вычислив элементы матрицы и вектора свободных членов, решив полученную систему уравнений, определив неизвестные коэффициенты в 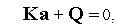 найдем приближенное решение поставленной задачи.
найдем приближенное решение поставленной задачи.
Решение задач микроуровня методом взвешенных невязок в инженерной практике крайне затруднительно из-за необходимости вычислять сложные двойные (для плоских задач) и тройные интегралы (для объемных задач) для объектов с криволинейными границами. При этом возникает противоречие между точностью решения, для обеспечения которой необходимо увеличивать степень аппроксимирующего полинома и сложностью вычисления интегралов.
Для разрешения этого противоречия было предложено разбить исследуемую область  на конечные элементы простой формы, чтобы вычисление интегралов по ним не представляло больших сложностей, а необходимой точности достигать увеличением числа конечных элементов. То есть в рамках метода взвешенных невязок необходимо перейти от интеграла по всей области к сумме
на конечные элементы простой формы, чтобы вычисление интегралов по ним не представляло больших сложностей, а необходимой точности достигать увеличением числа конечных элементов. То есть в рамках метода взвешенных невязок необходимо перейти от интеграла по всей области к сумме
интегралов по подобластям: |
где Е – число подобластей. |
Математическое обоснование такого перехода было выполнено с использованием глобальных базисных функций, равных единице в узле аппроксимации (узле сетки) и нулю во всех остальных узлах. В области КЭ от узла до границы базисные функции равномерно спадают от 1 до 0.

Пример базисных функций для одномерной задачи
Поскольку всего лишь одна из глобальных базисных функций принимает в узле значение равное 1, а остальные равны 0, то искомые коэффициенты 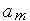 получают конкретный смысл — они равны значению функции в этом узле. Поэтому этап подстановки
получают конкретный смысл — они равны значению функции в этом узле. Поэтому этап подстановки  в
в
аппроксимацию для получения решения будет отсутствовать. При этом определенный интеграл |
после раскрытия (или |
взятия каким либо численным методом) приводит к математической модели конечного элемента в форме: |
где Kл - |
локальная матрица жесткости, Vл - вектор фазовых переменных, Qл - локальный вектор нагрузок. |
|
После ансамблирования получаем математическую модель системы в виде :
где K - матрица жесткости (глобальная) , V - вектор фазовых переменных, Q - вектор нагрузок (глобальный), 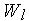 - весовые функции. Матрица является вектором, состоящим из компонент перемещений в вершинах элементов, которые определяются при решении системы уравнений. Она называется обобщенной матрицей жесткости системы и формируется по особым правилам из матриц жесткости отдельных элементов. Элементы обобщенной матрицы жесткости, являющиеся коэффициентами алгебраических уравнений, зависят только от координат вершин элементов и показателей деформируемости среды. Сложность конечного выражения обобщенной матрицы жесткости не зависит от степени неоднородности исследуемой области, т. е. каждый элемент может иметь свойства, отличающиеся от других.
- весовые функции. Матрица является вектором, состоящим из компонент перемещений в вершинах элементов, которые определяются при решении системы уравнений. Она называется обобщенной матрицей жесткости системы и формируется по особым правилам из матриц жесткости отдельных элементов. Элементы обобщенной матрицы жесткости, являющиеся коэффициентами алгебраических уравнений, зависят только от координат вершин элементов и показателей деформируемости среды. Сложность конечного выражения обобщенной матрицы жесткости не зависит от степени неоднородности исследуемой области, т. е. каждый элемент может иметь свойства, отличающиеся от других.
Разбиение области на конечные элементы — процедура построения сетки в методе конечных элементов. В отличие от метода конечных разностей выполняется, как правило, с помощью нерегулярной сетки. При этом во внимание может приниматься
априорная информация о градиентах фазовых переменных. Там, где возможны резкие изменения фазовой переменной, сетка строится более густой. При формировании сетки также следует стремиться к получению элементов возможно более "правильной" формы — при
использовании треугольных элементов избегать треугольников с очень острыми углами, при использовании прямоугольных элементов стремиться сделать элемент близким к квадрату – это позволяет повысить точность решения.
При нанесении сетки можно комбинировать элементы, например для обеспечения более точной аппроксимации границ. На рис.1 представлен объект с прямоугольными, треугольными и смешанными конечными элементами. Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники. Эта задача успешно решена на основании триангуляции Делоне.
Рис. 1. Разбиение области на конечные элементы. Зачерненная область показывает погрешность
представления области.
Алгоритм решения стационарных задач методом конечных элементов
Выбор формы конечного элемента.
Выбор функции формы (аппроксимации) конечного элемента. Разбиение области на конечные элементы.
Получение локальных матрицы жесткости и вектора нагрузок. Ансамблирование.
Учет граничных условий.
Решение системы алгебраических уравнений. После решения системы уравнений получаем значения фазовых переменных в узлах сетки.
Для практического применения МКЭ необходимо предварительно разработать математические модели конечных элементов (КЭ) и реализовать их в библиотеке КЭ программы анализа механической прочности. Основой математической модели 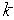 -го КЭ является
-го КЭ является
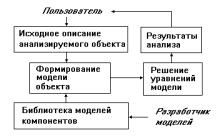
квадратная матрица жесткости 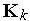 конечного элемента. Размер есть произведение размерности
конечного элемента. Размер есть произведение размерности  пространства и числа
пространства и числа 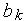 узлов,
узлов,
выделенных в модели 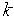 -го КЭ. Например, размер
-го КЭ. Например, размер  для КЭ в форме параллелепипеда с восемью узлами равен 24×24. При наличии библиотеки КЭ применение МКЭ сводится к следующим операциям (выполняются инженером):
для КЭ в форме параллелепипеда с восемью узлами равен 24×24. При наличии библиотеки КЭ применение МКЭ сводится к следующим операциям (выполняются инженером):
1.Создание геометрической модели исследуемой среды (например, детали) с помощью программы геометрического моделирования или путем изображения вручную на экране дисплея эскиза (чертежа) изделия.
2.Выбор библиотечной модели КЭ, задание внешних нагрузок и значений геометрических и физических параметров, формулировка граничных условий.
Формирование модели в маршруте проектирования. Вычислительный процесс при инженерном анализе состоит из этапов формирования модели и ее исследования. Формирование модели включает также две процедуры – разработку модели отдельных компонентов и формирование модели системы из моделей компонентов. Инженер, как правило, использует в работе библиотечные модели компонентов при формировании модели системы. Процедура анализа выполняется автоматически, по алгоритмам, включенным в программу анализа, например, анализ нагрузок в программе ANSYS. Модели компонентов разрабатываются специалистами в прикладных областях, знающими требования к моделям и формы их представления в САПР.
Рис. Формирование модели системы из моделей компонентов
Следующие операции выполняются программой моделирования:
3.Реализация в модели сетки конечных элементов. Тем самым становятся известными координаты узловых точек в модели.
4.Приведение имеющихся объемных сил и поверхностных нагрузок к узловым точкам модели.
5.Объединение моделей КЭ в общую конечно-элементную модель детали, в которой матрица жесткости К имеет порядок, равный d x b, где b — общее число узлов. При объединении элементы матрицы K образуются суммированием тех элементов матриц
жесткости отдельных КЭ, которые относятся к одному и тому же узлу и направлению перемещения. Если некоторый узел закреплен (его перемещение равно нулю), то соответствующие этому узлу строки в K и Q  и столбцы в K вычеркиваются.
и столбцы в K вычеркиваются.
6.Решение системы.
7.Представление результатов решения в удобной для пользователя форме. Наряду с числовым выводом результатов обычно используется графическое изображение деформированной детали, возможно представление распределений напряжений, деформаций, температур и т.п. внутри детали с указанием их интенсивности с помощью цветовой раскраски.
К числу известных программ анализа по МКЭ относятся ANSYS, NASTRAN, PATRAN.
ANSYS — универсальная программная система конечно-элементного (МКЭ) анализа, существующая и развивающаяся на протяжении последних 30 лет для решения линейных и нелинейных, стационарных и нестационарных пространственных задач механики, деформируемого твёрдого тела и механики конструкций. Она включает нестационарные геометрически и физически нелинейные задачи контактного взаимодействия элементов конструкций, задачи механики жидкости и газа, теплопередачи и теплообмена, электродинамики, акустики, а также механики связанных полей. Моделирование и анализ позволяет избежать дорогостоящих и длительных циклов разработки типа «проектирование — изготовление — испытания». Система работает на основе геометрического ядра Parasolid. Как программная система ANSYS сопрягается с известными CAD-системами Unigraphics, CATIA, Pro/ENGINEER, SolidEdge, SolidWorks, Autodesk Inventor и некоторыми другими. Программная система ANSYS используется на таких предприятиях, как BMW, Boeing, Caterpillar, Daimler-Chrysler, Exxon, FIAT, Ford, General Electric, Lockheed Martin, MeyerWerft, Mitsubishi, Siemens, Shell, Volkswagen-Audi и др.
Семейство продуктов ANSYS
PrepPost. Полнофункциональная итерактивная среда включает пре- и пост процессоры для создания геометрической модели исследуемой среды, детали, импорту-экспорту изображений, автоматическому построению КЭ сеток, постановке задачи, операции с результатами - все, за исключением собственно решения задачи.
Professional - Высокоэффективный комбинированный пакет, предназначен для расчета линейных статических задач прочности (ориентирован на инженеров среднего звена).
Structural - Полный прочностной пакет включает функции прочностного анализа, контактные задачи. Частотная область динамического анализа (гармонический, спектральный, вибрации). Динамический анализ неустановившихся процессов; устойчивость конструкций; механика разрушения.
Расчетные возможности: http://ansys.soften.com.ua/products/38-mechanical.html
Прочность
-Статика -Собственные частоты и формы колебаний
-Критические частоты вращения валов с учетом гироскопического эффекта -Гармонический анализ -Спектральный анализ и случайные колебания -Устойчивость конструкций -Линейные расчеты
-Нелинейные расчеты: большие деформации, напряженная жесткость
Контактные задачи
-Контакт деформируемых тел -Контакт деформируемого тела с жестким телом Формулировки контакта -Штрафные функции
-Метод множителей Лагранжа -Модифицированный метод Лагранжа
Свойства контакта -Трение -Температурные перепады
Электрические и магнитные задачи -Точечная сварка
Граничные/начальные условия Ввод нагрузок в форме таблиц или функций
Модели материалов
-Линейная упругая Неупругие
-Независящие/зависящие от скорости деформирования -Сплавы с памятью формы -Чугун
Гиперупругость, вязкопластичность и вязкоупругость Ползучесть и радиационное распухание Пьезоэлектрические свойства
Теплоемкость
-Температуро- и электропроводность -Демпфирование в материале
Теплопередача
-Стационарные и нестационарные задачи -Теплообмен конвекцией/излучением
Оптимизация
-Оптимизация параметров/ топологии -Параметрическое моделирование
Методы решения
-Итерационные
-Сопряженных градиентов с предобуславливанием (PCG) -Сопряженных градиентов по Якоби (JCG)
-Сопряженных градиентов с неполным разложением Холецкого (ICCG) Прямые
-Разреженный -Фронтальный
Многопроцессорные версии
-Распараллеленный PCG
-Распараллеленный JCG -Распараллеленный многосеточный (AMG) -Декомпозиции (DDS)
Решение задач на собственные значения
-Блочный метод Ланцоша -Интегрирование подпространства -Метод редуцирования
-QR-разложение для задач с демпфированием
Элементы
-2D и 3D объемные КЭ (солиды) и гиперупругие -Оболочечные элементы -Балочные КЭ -Трубчатые КЭ
-2D и 3D
-Опция "Рождение-смерть"
Платформы для среды ANSYS Workbench: Intel IA-32 Windows, HP PA 8000 64-bit, Sun UltraSPARC 64-bit, Intel IA-32 LINUX
Multiphysics - Наиболее полный пакет, включающий в себя все возможные физические дисциплины (прочность и тепло), а также электромагнитный анализ (магнитостатика, электростатика, электропроводность, низкочастотный гармонический анализ, высокочастотный анализ) и гидрогазодинамику (стационарная и нестационарная, сжимаемые и несжимаемые, ламинарные и турбулентные потоки; естественная и вынужденная конвекция, сопряженный теплоперенос; вязкие и многокомпонентные течения; фильтрация).
LS-DYNA - специализированные контактные алгоритмы, множество уравнений состояния и метод интегрирования, что позволяет численно моделировать процессы формования материалов, анализа аварийных столкновений и ударов при конечных деформациях.
ICEM CFD Комплексная система генерации любых типов расчетных сеток имеющая прямой интерфейс с CAD системами (Pro/E, Catia, Unigraphics). Экспорт сетки в более чем в 100 пакетов гидрогазодинамического и структурного анализа. Анализ и исправление геометрии, пре и пост-процессинг, адаптивная оптимизация сетки
CFX - Программный комплекс, сочетающий уникальные возможности анализа
гидрогазодинамических процессов, многофазных потоков, химической кинетики, горения, радиационного теплообмена
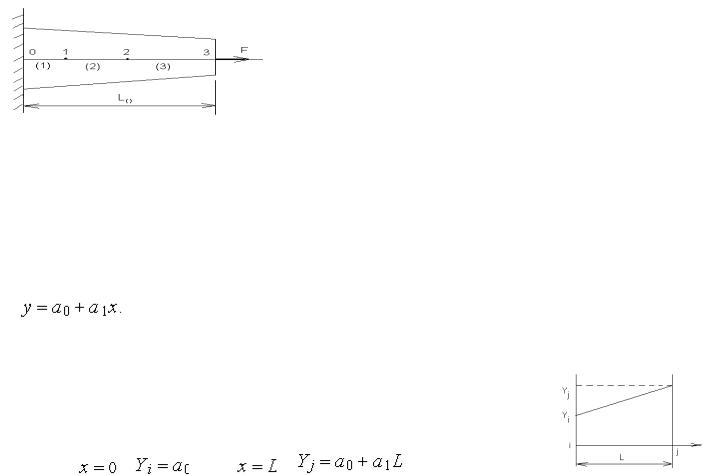
Пример решения одномерной задачи с помощью МКЭ
Пусть необходимо найти удлинение балки, с одним закрепленным концом (см. рис. 1) с продольной нагружающей силой.
Рис. 1.
Уравнение, описывающее состояние балки имеет вид: 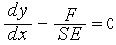 ; здесь
; здесь  — удлинение,
— удлинение, 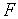 — нагружающая сила,
— нагружающая сила, 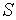 — площадь поперечного сечения,
— площадь поперечного сечения, 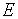 — модуль Юнга.
— модуль Юнга.
В соответствии с алгоритмом решения стационарных задач с помощью МКЕ:
1.Выбираем конечный элемент. Для одномерной задачи выбор ограничен только отрезком прямой.
2.Выбираем функцию формы конечного элемента, то есть фактически выбираем аппроксимацию решения внутри конечного элемента. Будем считать, что удлинение внутри конечного элемента меняется по линейному закону:
(1)
Предполагаем, что нам известны узловые значения удлинений, 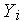 и
и 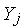 (см. рис. 2):
(см. рис. 2):
Из (1) при |
: |
, при |
: |
. |
Рис. 2. |
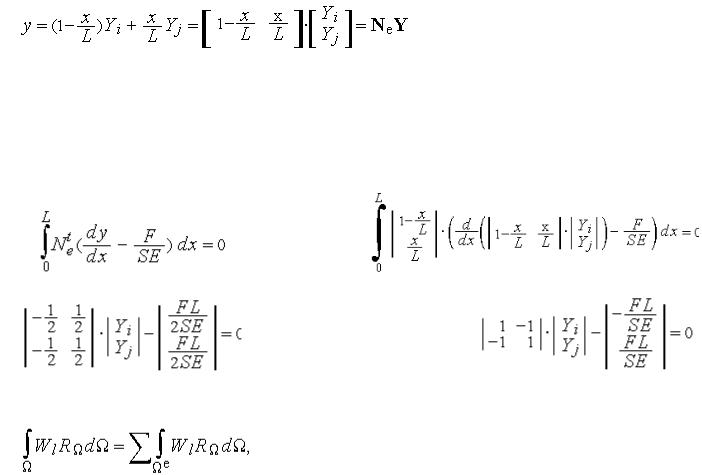
Из данной системы уравнений находим значения  и
и 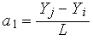 и подставляем в (1), выделяя коэффициенты при
и подставляем в (1), выделяя коэффициенты при 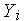 и
и 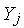 :
:
где 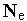 — вектор функции формы конечного элемента, его составляющие элементы — глобальные базисные функции, отличные от нуля в пределах этого элемента.
— вектор функции формы конечного элемента, его составляющие элементы — глобальные базисные функции, отличные от нуля в пределах этого элемента.
3.Разбиваем область на конечные элементы. В отличие от метода конечных разностей разбиение может быть совершенно произвольно. При этом следует принимать во внимание априорно известное распределение фазовой переменной: там, где возможно резкое изменение фазовой переменной, сетку следует делать более густой.
4.Получение локальных матрицы жесткости и вектора нагрузок конечного элемента. Локальная матрица жесткости и вектор
нагрузок — математическая модель конечного элемента. Фактически для их получения необходимо применить метод взвешенных невязок в пределах конечного элемента с аппроксимацией, полученной в п. 2. В соответствии с методом Галеркина в качестве весовых используются пробные функции:
или Раскрываем интеграл в предположении, что площадь поперечного сечения элемента постоянна:
(2)
Приводим уравнение к следующему виду (2) (умножением на 2): Получили локальные матрицу жесткости и вектор нагрузок.
5. Ансамблирование. Ансамблирование выполняется в соответствии с основной идеей МКЭ, согласно которой
- то есть интеграл по всей области равен сумме интегралов по подобластям. Интеграл по одному конечному элементу мы вычислили в (2).
Глобальная матрица жесткости будет иметь размерность, определяемую числом узлов сетки, в нашем примере — 4. Вектор неизвестных составляют перемещения в этих узлах. Локальная матрица жесткости каждого конечного элемента даст аддитивный вклад в глобальную матрицу в соответствии с узлами подключения конечного элемента (это же касается и вектора нагрузок). Смысл глобальной единичной матрицы – определение и учет направлений сил в каждой точке разбиения:

-в точке 0 действуют две противоположные силы вдоль оси х, 1 и -1
-на точку 1 действует сила со стороны точки 0 (-1), две силы в сторону точки 2 и реакция со стороны точки 2 (-1)
-и так далее до точки 3, на которую действует сила со стороны точки 2(равная -1) и сила вдоль оси х (1). Получилась матрица перед столбцом Y
6.Учет граничных условий . В нашем примере 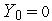 , то есть можно вычеркнуть первый столбец и первую строку.
, то есть можно вычеркнуть первый столбец и первую строку.
7.Решение системы уравнений. В результате найдем удлинение в каждом узле.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
HFSS – стандартизованное программное обеспечение для получения S-параметров, создания SPICE-моделей (параметров микросхем, позволяющих
рассчитать режимы по постоянному току, передаточные функции, импедансы, шумы, переходные процессы и пр.) и трехмерного моделирования электромагнитного поля для высокочастотных и высокоскоростных компонентов. HFSS эффективна при проектировании встроенных в кристалл пассивных элементов, корпусов интегральных схем, разводки печатных плат, антенн, ВЧ/СВЧ компонентов и биомедицинских устройств.
HFSS использует метод конечных элементов для расчета электрического поведения высокочастотных и высокоскоростных компонентов. При
помощи HFSS инженеры могут получать эквивалентные параметры (S, Y, Z), трехмерное изображение электромагнитных полей (в ближней и дальней зоне), создавать SPICE-модели для эффективной оценки качества сигнала, оценивать потери в линиях передач, потери на отражение, возникающие в следствие разных импедансов, паразитные связи и излучения.
Основу решения трехмерных и двумерных задач электродинамики в HFSS составляет метод конечных элементов (МКЭ). Смысл метода состоит в том, что пространство, в котором распространяются электромагнитные волны, разбивается на простейшие объемные элементы, имеющие форму тетраэдров. Разбиение осуществляется специальной программой Mesher, входящей в состав HFSS. Размер тетраэдра должен быть достаточно мал для того, чтобы поле в его пределах можно было описать простой функцией или набором функций с неизвестными коэффициентами. Эти коэффициенты ищутся из

уравнений Максвелла и граничных условий. В результате электродинамическая задача сводится к системе линейных алгебраических уравнений (СЛАУ) относительно этих коэффициентов. Решение СЛАУ находится численным методом на ЭВМ.
|
Название |
Дифференциальная |
|
Интегральная |
Примерное словесное выражение |
||
|
|
||||||
|
форма |
|
форма |
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
Закон индукции Фарадея |
rotE=−∂B/∂t |
|
LEdl=−∫S∂B∂tdS |
Изменение магнитной индукции порождает вихревое электрическое поле |
||
|
|
|
|
|
|
|
|
|
Закон Ампера |
rotH=j+∂D/∂t |
|
LHdl=Iencl+ |
|
S∂D∂tdS |
Электрический ток и изменение электрической индукции порождают вихревое магнитное |
|
добавкой |
||||||
|
|
||||||
|
от(сМаксвелла) |
|
|
|
поле |
||
|
Теорема Гаусса |
divD=ρ |
|
SDdS=Qencl |
|
|
Электрический заряд является источником электрической индукции |
|
|
|
|
|
|
|
|
|
Теорема Гаусса |
divB=0 |
|
SBdS=0 |
|
|
Магнитная индукция не имеет источников. |
|
|
|
|
|
|
|
|
Введённые обозначения:
ρ — плотность стороннего электрического заряда (в единицах СИ — Кл/м³)
j — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²)
E — напряжённость электрического поля (в единицах СИ — В/м)
H — напряжённость магнитного поля (в единицах СИ — А/м)
D — электрическая индукция (в единицах СИ — Кл/м²)
B — магнитная индукция (в единицах СИ — Тл = Вб/м²= кг·с-2·А-1)
Qencl — сторонний электрический заряд, заключенный внутри поверхности S (в единицах СИ — Кл)
Iencl — электрический ток, проходящий через поверхность S вызванный движением свободных зарядов (в единицах СИ — А)
rot — дифференциальный оператор ротора
div — дифференциальный оператор дивергенции
S — замкнутая двумерная поверхность
L — замкнутый контур

Лекция 7. Макроуровень
На макроуровне используют укрупненную дискретизацию пространства по функциональному признаку. Независимой переменной является время t, а зависимыми являются силы и скорости в механических системах, напряжения и токи в электрических системах, давления и расходы жидкостей и газов в гидравлических и пневматических системах и т.п. Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения.
Компонентными называют уравнения, описывающие свойства элементов (компонентов), другими словами, математическая модель элемента (ММЭ) представляется компонентными уравнениями.
Топологические уравнения описывают взаимосвязи в составе моделируемой системы. В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель
системы (ММС).
Компонентные и топологические уравнения в системах различной физической природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. Одинаковая форма записи математических соотношений позволяет говорить о формальных аналогиях компонентных и топологических уравнений. Такие аналогии существуют для механических поступательных, механических вращательных, электрических, гидравлических (пневматических), тепловых объектов. Наличие аналогий приводит к практически важному выводу:
значительная часть алгоритмов формирования и исследования моделей в САПР оказывается инвариантной и может быть применена к анализу проектируемых объектов в разных предметных областях. Единство математического аппарата формирования ММС особенно удобно при анализе систем, состоящих из физически разнородных подсистем.
В перечисленных выше приложениях компонентные уравнения имеют вид:
|
|
|
(1) |
топологические уравнения: |
|
|
|
где |
— вектор фазовых переменных, |
— время. |
(2) |
Различают фазовые переменные двух типов, их обобщенные наименования — фазовые переменные типа потенциала (например, электрическое напряжение) и фазовые переменные типа потока (например, электрический ток). Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение — связи между однотипными фазовыми переменными в разных компонентах. Модели можно представлять в виде систем уравнений или в графической форме, если между этими формами установлено взаимно однозначное соответствие. В качестве графической формы часто используют эквивалентные схемы.
Электрические системы
В электрических системах фазовыми переменными являются электрические напряжения и токи. Компонентами систем могут быть простые двухполюсные элементы и более сложные двух- и многополюсные компоненты. К простым двухполюсникам
относятся следующие элементы: сопротивление, емкость и индуктивность, характеризуемые параметрами 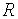 ,
, 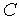 ,
, 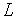 .
.
Компонентные уравнения простых двухполюсников:
для сопротивления (закон Ома): u = iR |
(3) |
для емкости: |
(4) |
для индуктивности: |
(5) |
где  — напряжение (точнее, падение напряжения на двухполюснике);
— напряжение (точнее, падение напряжения на двухполюснике); 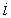 — ток.
— ток.
Эти модели лежат в основе моделей других возможных более сложных компонентов. Большая сложность может определяться нелинейностью уравнений (3) — (5) (т.е. зависимостью 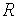 ,
,  ,
,  от фазовых переменных), или учетом зависимостей
от фазовых переменных), или учетом зависимостей
параметров  ,
,  ,
,  от температуры, или наличием более двух полюсов. Однако многополюсные компоненты могут быть сведены к совокупности взаимосвязанных простых элементов.
от температуры, или наличием более двух полюсов. Однако многополюсные компоненты могут быть сведены к совокупности взаимосвязанных простых элементов.
Топологические уравнения выражают законы Кирхгофа для напряжений (ЗНК) и токов (ЗТК). Согласно ЗНК, сумма напряжений на компонентах вдоль любого замкнутого контура в эквивалентной схеме равна нулю, а в соответствии с ЗТК сумма токов в любом замкнутом сечении эквивалентной схемы равна нулю:
(6)
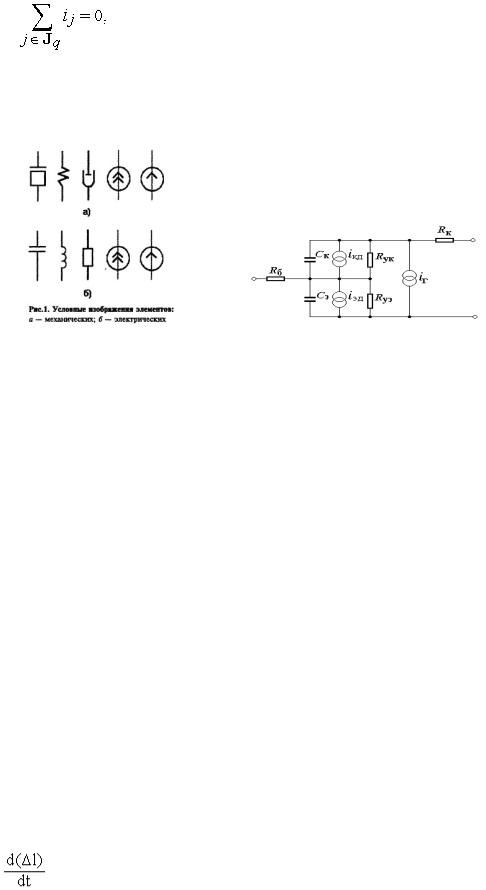
(7)
где:  — множество номеров элементов
— множество номеров элементов  -го контура;
-го контура;  — множество номеров элементов, входящих в
— множество номеров элементов, входящих в 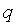 -е сечение. Двойная стрелка – источник тока (ri =oo), одинарная - источник напряжения (ri =0). В механике двойная стрелка - поток
-е сечение. Двойная стрелка – источник тока (ri =oo), одинарная - источник напряжения (ri =0). В механике двойная стрелка - поток
(сила F), одинарная – потенциал (скорость V)
Рис. 2. Эквивалентная схема биполярного
транзистора Примером ММ сложного компонента может служить модель транзистора.
На рис. 2 представлена простейшая эквивалентная схема биполярного транзистора, на которой зависимые от напряжений
источники тока 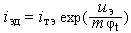 и
и 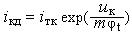 отображают статические вольтамперные характеристики p-n
отображают статические вольтамперные характеристики p-n
переходов, 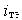 и
и 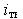 — тепловые токи переходов,
— тепловые токи переходов, 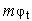 — температурный потенциал,
— температурный потенциал,  и
и 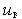 — напряжения на эмиттерном и коллекторном переходах,
— напряжения на эмиттерном и коллекторном переходах, 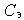 и
и 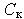 — емкости переходов,
— емкости переходов, 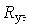 и
и 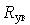 — сопротивления утечки переходов,
— сопротивления утечки переходов, 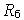 и
и 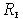 — объемные сопротивления тел базы и коллектора,
— объемные сопротивления тел базы и коллектора, 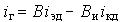 — источник тока, моделирующий усилительные свойства
— источник тока, моделирующий усилительные свойства
транзистора,  и
и  — прямой и инверсный коэффициенты усиления тока базы. Здесь
— прямой и инверсный коэффициенты усиления тока базы. Здесь 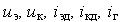 — фазовые переменные, а остальные величины — параметры модели транзистора. Модель Эберса-Молла – включает 14, Гуммеля-Пуна -25 параметров.
— фазовые переменные, а остальные величины — параметры модели транзистора. Модель Эберса-Молла – включает 14, Гуммеля-Пуна -25 параметров.
Механические системы
Фазовыми переменными в механических поступательных системах являются силы и скорости.
Эквивалентные схемы механических поступательных подсистем
Переменной типа потока является сила F, переменной типа потенциала - скорость V. Простейшие элементы: трение K, масса m, упругость С, компонентные уравнения которых:
F= kV , F=m 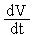 , V=
, V= 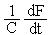
и источники силы и скорости с компонентными уравнениями: F=F(Z), V=V(Z), где в качестве Z может фигурировать время или фазовая переменная.
Компонентное уравнение элемента упругости может быть получено как из уравнения линейной пружины, так и из закона Гука. Для линейной пружины справедливо уравнение: F=C*X, где X - взаимное смещение концов пружины, путем дифференцирования уравнения по времени получим 3-е компонентное уравнение.
Для упругой балки справедливо уравнение Гука 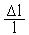 =
=  , где Δlотносительное удлинение, l - длина, S - площадь поперечного сечения , E - модуль Юнга. Дифференцируя по времени получим:
, где Δlотносительное удлинение, l - длина, S - площадь поперечного сечения , E - модуль Юнга. Дифференцируя по времени получим:
= 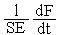 , или V=
, или V= 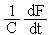 , где C=
, где C=  .
.
Нетрудно заметить наличие аналогий между электрической и механической системами. Так, токам и напряжениям в первой из них соответствуют силы (либо моменты) и скорости механической системы, компонентным уравнениям и фигурирующим в них
параметрам 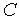 и
и 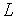 — уравнения и параметры
— уравнения и параметры 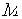 и
и 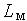 , очевидна аналогия и между топологическими уравнениями. Далее параметры
, очевидна аналогия и между топологическими уравнениями. Далее параметры 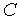 и
и 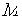 будем называть емкостными (емкостного типа), параметры
будем называть емкостными (емкостного типа), параметры  и
и  — индуктивными (индуктивного
— индуктивными (индуктивного
типа), а параметры  и
и 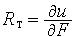 — резистивными (резистивного типа).
— резистивными (резистивного типа).
Условные изображения элементов на эквивалентных схемах представлены на рис.
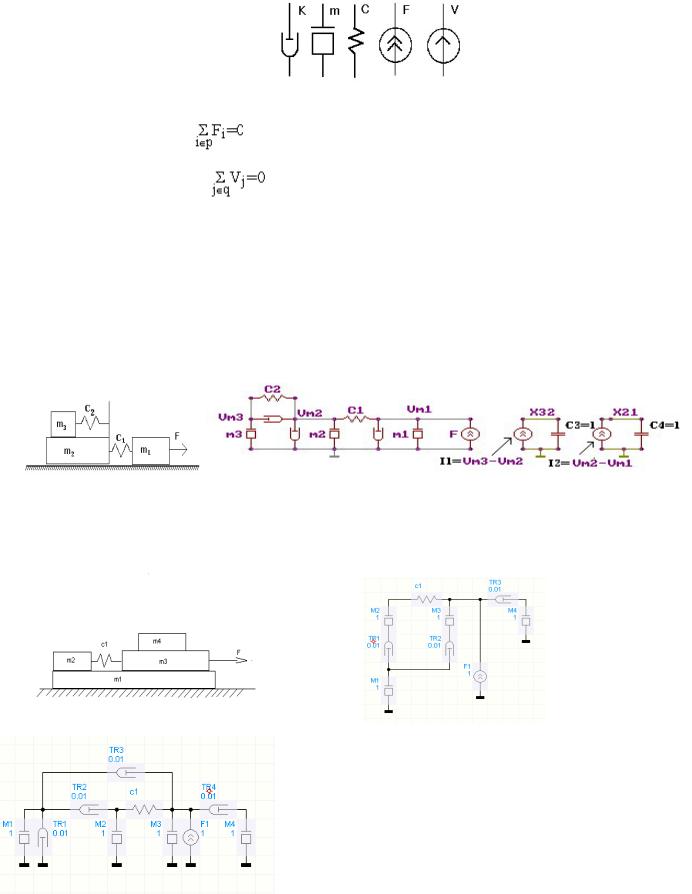
Топологические уравнения: |
|
|
|
|
|
|
|
а) уравнение равновесия |
(принцип Даламбера)- сумма сил инерции, активных и реактивных равна 0. |
||
б) уравнение непрерывности |
|
(принцип сложения скоростей) Скорость движения тела относительно |
|
неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
Алгоритм составления эквивалентных схем
1.Выбирается инерциальная система отсчета. В большинстве инженерных приложений в качестве таковой можно принять землю. Инерциальной системе отсчета в эквивалентной схеме соответствует базовый узел.
2.В подсистеме выделяются элементы, у которых необходимо учесть массу, эти элементы считаются абсолютно жесткими. На эквивалентной схеме такие элементы одним полюсом всегда подключаются к базовому узлу. Все взаимодействия с остальными элементами осуществляются через второй полюс.
3.Между соответствующими узлами включаются элементы упругости и трения.
Рассмотрим пример составления эквивалентной схемы для поступательной механической подсистемы представленной на рис.2.
Рис. 2.
Считаем массы m1 - m3 абсолютно жесткими, пружины С1,С2 - безынерционными. Элементы С1 и С2 являются нелинейными и изменяют свои параметры в зависимости от смещения концов пружин, поэтому необходимо ввести в эквивалентную схему два интегратора, состоящих из элементов I1, С3 и I2, С4, позволяющих получить смещения в качестве потенциалов узлов X32 и X21.
Исходя из этих предположений, эквивалентная схема показана на следующем рисунке.
Эквивалентные схемы для следующей механической поступательной системы изображены ниже:
Имеется существенное отличие в моделировании электрических и механических систем: первые из них одномерны, а процессы во вторых часто приходится рассматривать в двух- (2D) или трехмерном (3D) пространстве. Следовательно, при моделировании механических систем в общем случае в пространстве 3D нужно использовать векторное представление фазовых переменных, каждая из которых имеет три составляющих. Для каждой степени свободы строят свою эквивалентную схему. Каждому телу с учитываемой массой соответствует узел схемы (вершина графа). Один узел, называемый базовым, отождествляется с инерциальной системой отсчета. Внешние воздействия моделируются источниками сил и скоростей.
В качестве примера изображена некоторая механическая система — тележка, движущаяся по дороге и состоящая из платформы A, колес B1, B2 и рессор C1, C2. Приведена эквивалентная схема для вертикальных составляющих сил и скоростей, на

которой телам системы соответствуют одноименные узлы, учитываются массы платформы и колес, упругость рессор, трение между колесами и дорогой. Неровности дороги вызывают воздействие на систему, изображенное на рис. источниками силы.
Рис. 3 Эквивалентная схема механической системы
Эквивалентные схемы механических вращательных подсистем
Переменной типа потока является момент силы M, переменной типа потенциала - угловая скорость ω. Простейшие элементы: трение K, момент инерции J, вращательная упругость C, компонентные уравнения которых
M=Kω , M=J |
, ω= |
, и источники момента силы и угловой скорости с компонентными уравнениями: |
M=M(z) , ω=ω(Z), |
где в качестве Z может фигурировать время или фазовая переменная. |
|
Компонентное уравнение вращательной упругости может быть получено как из уравнения спиральной пружины, так и из уравнения кручения бруса с круглым поперечным сечением. Для линейной спиральной пружины справедливо уравнение: M=Cφ , где φ - угол закручивания пружины. Дифференцируя по времени получим 3-е компонентное уравнение вращательной упругости. Для бруса с круглым поперечным сечением справедливо уравнение: M = GJpθ, где М - крутящий момент, G - модуль сдвига ,
Jp - полярный момент инерции сечения, θ= относительный угол закручивания. Для бруса конечной длины θ=  , где φ- угол закручивания , l - длина бруса. Продифференцировав обе части уравнения по времени получим:
, где φ- угол закручивания , l - длина бруса. Продифференцировав обе части уравнения по времени получим:
= |
, или ω= |
где C= |
. |
Условные изображения на эквивалентных схемах представлены на рис.
Топологические уравнения для механической вращательной подсистемы.
а) уравнение равновесия |
(принцип Даламбера для вращательных подсистем) |
б) уравнение непрерывности |
(принцип сложения скоростей) |
Эквивалентные схемы гидравлических закрытых подсистем
В гидравлических закрытых подсистемах влиянием высоты столба жидкости на давление можно пренебречь, так как рабочее давление существенно превышают те, которые обусловлены высотой столба жидкости.
Переменной типа потока является объемный расход G, переменной типа потенциала давление P.
Простейшие элементы: потеря давления R, сжимаемость Cg, инерционность Lg, компонентные уравнения которых:
G=  P, G=Cg
P, G=Cg  , P=Lg
, P=Lg 
и источники расхода и давления с компонентными уравнениями
G=G(Z), P=P(Z), где в качестве Z может фигурировать время или фазовая переменная.
Топологические уравнения - гидравлическая (пневматическая) закрытая подсистема.
а) уравнение равновесия Gi=0 (сумма расходов в узле равна нулю)
б) уравнение непрерывности Pj=0 (сумма разностей давлений при обходе по замкнутому контуру равна нулю)
Алгоритм составления эквивалентных схем
1.Базовый узел эквивалентной схемы соответствует точке отсчета давления - либо абсолютному нулю, либо атмосферному давлению. Выбор точки отсчета зависит от реализованных в математических моделях зависимостях, например, зависимости модуля упругости от газосодержания и температуры.
2.В подсистеме выделяются элементы, сжимаемость жидкости в которых оказывает существенное влияние на динамику подсистемы, как правило это резервуары значительного объема. На эквивалентных схемах такие элементы одним полюсом подключаются к базовому узлу. Все взаимодействия с окружающей средой осуществляются через второй полюс.
3.В гидравлических подсистемах, кроме резервуаров, из пассивных элементов присутствуют дроссели и трубопроводы. Они включаются между соответствующими резервуарами или между собой. Трубопровод, когда можно пренебречь волновыми процессами, отображается элементом потерь или последовательно включенными элементом потерь и элементом инерционности, в противном случае необходимо использовать более сложные модели, например модели с распределенными параметрами.
4.Активные компоненты - насосы, аккумуляторы давления отображаются на эквивалентных схемах в виде источников расхода и давления ограниченной мощности.
Пример эквивалентной схемы для гидравлической подсистемы представлен на рис.4. Дроссели Д1-Д3 представлены элементами потери давления R1-R3, трубопроводы от насоса Н к резервуарам С1-С3 элементами R4-R6.
Рис. 4.
Эквивалентные схемы гидравлических открытых подсистем
В открытых гидросистемах давления определяются высотой столба жидкости или напором h, поэтому переменной типа потенциала можно выбрать эту величину, а переменной типа потока, как и в закрытых подсистемах, оставить объемный расход G. Сжимаемостью жидкости при давлениях, характерных для открытых гидросистем, можно пренебречь. Простейшие элементы:
потеря давления R, емкость C, инерционность L, компонентные уравнения которых:
G= 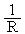 h, G=C
h, G=C 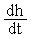 , h=L
, h=L 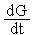
и источники расхода и напора с компонентными уравнениями:
G=G(Z) и h=h(Z), где в качестве Z может фигурировать время или фазовая переменная.
Алгоритм составления эквивалентных схем
1.Базовый узел эквивалентной схемы соответствует атмосферному давлению.
2.В подсистеме выделяются элементы, в которых возможно изменение уровня жидкости, на эквивалентных схемах такие элементы одним полюсом всегда подключаются к базовому узлу, все взаимодействия осуществляются через второй узел.
3.Трубопроводы отображаются также как в закрытых гидросистемах.
4.Слив из резервуара и перетекание жидкости из одного резервуара в другой моделируются с помощью зависимых источников расхода и давления, как это показано в следующем примере.
Для участка некоторой технологической цепочки, представленной на рис.3 составлена эквивалентная схема, показанная на рис.4
а) уравнение равновесия Gi=0 (сумма расходов в узле равна нулю)
б) уравнение непрерывности hj=0 (сумма разностей напоров при обходе по замкнутому контуру равна нулю).
Рис.5
Эквивалентные схемы тепловых подсистем
Переменной типа потока является тепловой поток Ф, переменной типа потенциала - температура Т. Простейшие элементы:
теплопроводность R, теплоемкость C, компонентные уравнения которых:
Ф= 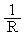 T , Ф=C
T , Ф=C 
и источники теплового потока и температуры с компонентными уравнениями:
Ф=Ф(Z), Т=Т(Z),
|
|
|
|
Рис. 6. |
нет |
Ф |
Т |
|
Алгоритм составления эквивалентных схем.
1.Базовый узел эквивалентной схемы соответствует условному телу с температурой 0С или 0K. Выбор точки отсчета зависит от реализации математических моделей элементов, но для всех элементов должен быть одинаков.
2.В подсистеме выделяются элементы, у которых необходимо учесть теплоемкость. На эквивалентных схемах такие элементы одним полюсом подключаются к базовому узлу. Весь теплообмен с данным элементом осуществляется через другой полюс.
3.Между соответствующими узлами включаются элементы теплопроводности.
Рассмотрим построение эквивалентной схемы для объекта, представленного на рис.2.
Рис.2 Рис.3 Здесь П-плита, Н - нагреватель с теплоемкостью Сн и мощностью Р. Считая, что плита расположена горизонтально,
теплоотдачей вниз от нее пренебрегаем. Представим плиту в виде четырех элементов с теплоемкостью каждого участка Сп. Для получения более точных результатов, необходима большая дискретизация, но в данном случае для иллюстрации получения эквивалентной схемы достаточно предложенного разбиения.
Сп - теплоемкость участка плиты, которая считается сосредоточенной в центре участка, R1-R4 -теплопроводности между участками платы, R5теплопроводность между нагревателем и платой, R6-R10 - конвекционные теплопроводности, Т- источник температуры, равный температуре окружающей среды, Ф=Р - источник теплового потока, определяемый мощностью нагревателя.
Топологические уравнения - тепловая подсистема.
а) уравнение равновесия |
Фi=0 (сумма тепловых потоков в узле равна нулю) |
б) уравнение непрерывности |
Тj=0 (сумма разностей температур при обходе по замкнутому контуру равна нулю) |
Типы связей между физическими однородными подсистемами
Типы связей между подсистемами можно классифицировать следующим образом:
1)трансформаторный
2)гираторный 3-4-5-дифференциальный, интегральный, через зависимые параметры.
Трансформаторный тип связи. Энергия (потенциальная) переходит в другой тип (кинетическую) с каким-то коэффициентом преобразования и потерями. Эквивалентная схема этого типа связи представлена на рис.1
Рис.1 Рассмотрим эквивалентную схему объекта, представленного на след. рисунке
Здесь источники V1 и M1 представляют трансформаторное взаимодействие поступательной подсистемы с массой m1 и вращательной, а источники V2 и M2 - взаимодействие поступательной подсистемы с массой m2 и вращательной.
Гираторный тип связи
Для этого типа можно предложить два равноценных варианта эквивалентных схем, которые отличаются использованием зависимых источников различных типов - потока (рис.4) или потенциала (рис.5).
Рис. 4. |
Рис. 5. |
Учитывая особенности методов формирования ММС предпочтение следует отдать первой схеме рис.4.
Рассмотрим этот вид взаимодействия при построении эквивалентной схемы простейшего одностороннего гидроцилиндра (рис.6). Предполагая, что корпус цилиндра неподвижен, можно построить эквивалентную схему, показанную на рис.7.
Рис. 6. |
Рис. 7. |
Здесь P - источник внешнего давления на входе в трубопровод, Rg и Lg - потери и инерция движения жидкости в трубопроводе, Сg - полость гидроцилиндра, М - масса поршня, TR1 - трение поршня о стенки, U1 - упругость штока от поршня до стенки, U2 - упругость остальной части штока, F2 - внешнее воздействие на шток. Источники Q и F - элементы гираторной связи с компонентными уравнениями G=V*S где S -площадь поперечного сечения поршня, V - скорость движения поршня, и F=Pc*S, Pc - давление в гидроцилиндре.
Формирование математической модели системы (ММС)
Известен ряд методов формирования ММС на макроуровне. Получаемые с их помощью модели различаются ориентацией на те или иные численные методы решения и набором базисных фазовых переменных, остающихся в уравнениях итоговой ММС. Общим
для всех методов является исходная необходимость получения информации об эквивалентной схеме и соединении элементов в узлы.
При записи топологических уравнений используют промежуточную графическую форму — представление модели в виде эквивалентной схемы, состоящей из двухполюсных элементов. Общность подхода при этом сохраняется, так как любой многополюсный компонент можно заменить подсхемой из двухполюсников.
Эквивалентную схему из двухполюсных элементов рассматривают как направленный граф, дуги которого соответствуют ветвям схемы. Граф, подграф, сурграф (подграф, включающий все вершины графа), нормальное дерево (фундаментальное дерево, которое не имеет циклов и любая пара вершин соединена единственным маршрутом) с ветвями, рассматриваемыми в
последовательности E, C, R, L, J
- эти понятия из теории графов понадобятся при рассмотрении. Направления потоков в ветвях выбираются произвольно (если реальное направление при моделировании окажется противоположным, то это приведет лишь к отрицательным численным значениям потока).
Пример некоторой простой эквивалентной схемы и соответствующего ей графа приведен на рис. 1,a. Для конкретности и простоты изложения на рис. 1,a использованы условные обозначения, характерные для электрических эквивалентных схем, и применяется электрическая терминология. Очевидно, что поясненные выше аналогии позволяют при необходимости легко перейти к обозначениям и терминам, привычным для механиков.
Рис. 1. Эквивалентная схема и соответствующий ей граф
Для получения топологических уравнений все ветви эквивалентной схемы разделяют на подмножества хорд и ветвей дерева.
Имеется в виду фундаментальное (покрывающее) дерево, т.е. подмножество из  дуг, не образующее ни одного
дуг, не образующее ни одного
замкнутого контура, где 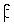 — число вершин графа (узлов эквивалентной схемы). На рис. показан граф эквивалентной схемы, толстыми линиями выделено одно из возможных покрывающих деревьев.
— число вершин графа (узлов эквивалентной схемы). На рис. показан граф эквивалентной схемы, толстыми линиями выделено одно из возможных покрывающих деревьев.
Выбор дерева однозначно определяет вектора напряжений 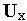 и токов
и токов 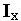 хорд, напряжений
хорд, напряжений 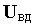 и токов
и токов  ветвей дерева и приводит к записи топологических уравнений в виде
ветвей дерева и приводит к записи топологических уравнений в виде
(1)
(2)
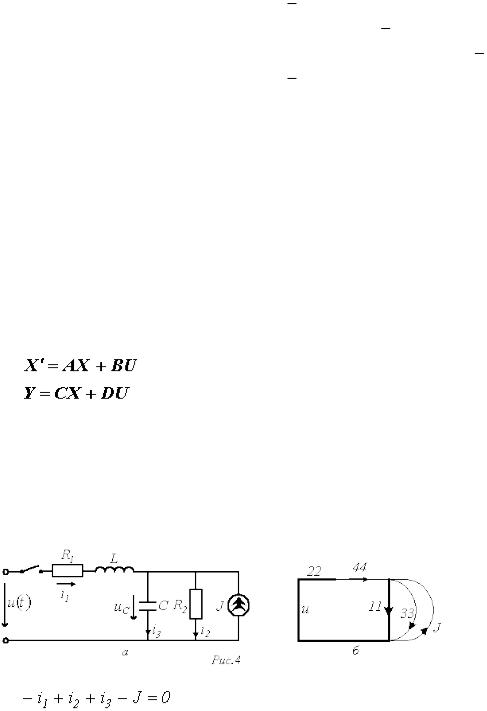
где 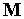 — матрица контуров и сечений ,
— матрица контуров и сечений , 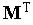 — транспонированная
— транспонированная  -матрица.
-матрица.
В случае электрических и гидравлических систем уравнения (1) представляют собой уравнения напряжений Кирхгофа для контуров, образованных поочередным подключением каждой из хорд в отдельности к дереву, а уравнения (2) — уравнения токов Кирхгофа для сечений ветвей дерева, т.е. для таких сечений, при которых пересекаются некоторые хорды и единственная ветвь дерева.
 -матрица несет информацию в заложенной структуре о порядке соединения элементов. Число строк соответствует числу хорд, число столбцов равно числу ветвей дерева.
-матрица несет информацию в заложенной структуре о порядке соединения элементов. Число строк соответствует числу хорд, число столбцов равно числу ветвей дерева. 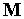 -матрица формируется следующим образом. Поочередно к дереву
-матрица формируется следующим образом. Поочередно к дереву
подключаются хорды. Если при подключении к дереву  -й хорды
-й хорды  -я ветвь входит в образовавшийся контур, то элемент
-я ветвь входит в образовавшийся контур, то элемент  матрицы равен
матрицы равен  при совпадении направлений ветви и подключенной хорды,
при совпадении направлений ветви и подключенной хорды, 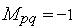 при несовпадении
при несовпадении
направлений. В противном случае 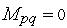 .
.
Для схемы на рис. 1,б  -матрица представлена в виде табл. 1.
-матрица представлена в виде табл. 1.
Таблица 1
Обозначение |
Ветвь C1 |
Ветвь C2 |
Ветвь C3 |
|
|
|
|
Хорда R1 |
1 |
0 |
0 |
|
|
|
|
Хорда R2 |
0 |
1 |
0 |
|
|
|
|
Хорда R3 |
0 |
0 |
1 |
|
|
|
|
Хорда R4 |
1 |
+1 |
+1 |
|
|
|
|
Хорда J |
+1 |
0 |
0 |
|
|
|
|
Второй шаг – решение ММ системы в виде полученных ОДУ+АУ тем или иным способом.
Метод переменных состояния
Уравнения электромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи. Метод переменных состояния позволяет представить математическую модель устройства в виде системы дифференциальных уравнений первого порядка относительно переменных состояния, вектора входных воздействий и вектора выходных параметров в виде, наиболее удобном для применения численных методов интегрирования.
Количество переменных состояния (число уравнений состояния), равно числу независимых накопителей энергии, в
качестве которых выступают токи индуктивностей  и производные
и производные 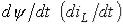 , напряжения (заряды)
, напряжения (заряды)
емкостей 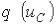 с производными
с производными 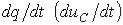 и источники внешних воздействий – ЭДС и тока.
и источники внешних воздействий – ЭДС и тока.
Полная система уравнений в матричной форме записи имеет вид |
|
; |
(2) |
|
|
. |
(3) |
|
Здесь  и
и  - столбцовые матрицы переменных состояния и их первых производных по времени; U - матрица-столбец источников внешних воздействий; Y - столбцовая матрица выходных (искомых) величин; A - квадратная размерностью n x n (где n – число переменных состояния) - матрица производных, называемая матрицей Якоби; B - прямоугольная матрица связи источников с переменными состояния (количество строк равно n, а столбцов – числу источников m); C - прямоугольная матрица связи переменных состояния с искомыми величинами (количество строк равно числу искомых величин к, а столбцов – n); D - прямоугольная размерностью к x m -матрица связи входа с выходом. Начальные условия для уравнения (2) задаются вектором
- столбцовые матрицы переменных состояния и их первых производных по времени; U - матрица-столбец источников внешних воздействий; Y - столбцовая матрица выходных (искомых) величин; A - квадратная размерностью n x n (где n – число переменных состояния) - матрица производных, называемая матрицей Якоби; B - прямоугольная матрица связи источников с переменными состояния (количество строк равно n, а столбцов – числу источников m); C - прямоугольная матрица связи переменных состояния с искомыми величинами (количество строк равно числу искомых величин к, а столбцов – n); D - прямоугольная размерностью к x m -матрица связи входа с выходом. Начальные условия для уравнения (2) задаются вектором
начальных значений 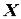 (0).
(0).
В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи 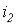 и
и 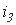 .
.
По законам Кирхгофа для данной цепи запишем |
|
; |
(4) |
|
(5)
|
; |
. |
(6) |
|
Поскольку 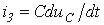 с учетом соотношения (6) перепишем уравнения (4) и (5) в виде
с учетом соотношения (6) перепишем уравнения (4) и (5) в виде
Вектор начальных значений  (0)= .
(0)= .
Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используем методику упорядоченного составления уравнений состояния, которая включает в себя следующие основные этапы:
1.Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС) в последовательности E, C, R, L, J. Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи (хорды) включаются катушки индуктивности, источники тока и оставшиеся резисторы.
2.Осуществляется нумерация ветвей графа (и элементов в схеме). Первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).
3.Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются ветви
-емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются хорды - резистивные и индуктивные элементы ветвей связи, а также источники тока.
Таблица соединений
 Ветви/хордыС->11
Ветви/хордыС->11 
 R1->22
R1->22 
 u
u
R2->33 |
-1 |
0 |
0 |
L->44 |
1 |
1 |
1 |
J |
1 |
0 |
|
Процедура заполнения таблицы заключается в поочередном мысленном замыкании ветвей дерева с помощью ветвей связи до получения контура с последующим обходом последнего согласно ориентации соответствующей ветви связи. Со знаком «+» записываются ветви графа, ориентация которых совпадает с направлением обхода контура, и со знаком «-» ветви, имеющие противоположную ориентацию. Осуществляется сканирование таблицы по столбцам и по строкам. В первом случае получаются уравнения по первому закону Кирхгофа, во втором – по второму.
В рассматриваемом случае (равенство 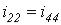 тривиально)
тривиально)
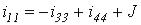 ,
,
откуда в соответствии с нумерацией токов в исходной цепи
.
При расписывании таблицы соединений по строкам напряжения на пассивных элементах необходимо брать со знаками, противоположными табличным:
(7)
Эти уравнения совпадают соответственно с соотношениями (6) и (5). Из (7) непосредственно вытекает
.
Таким образом, формализованным способом получены уравнения в форме Коши, аналогичные составленным выше с использованием законов Кирхгофа. http://www.ups-info.ru/for_partners/library/ teoreticheskie_osnove_ilektrotehniki_dlya_ibp_ups_/integral_dyuamelya_metod_peremenneh_sostoyaniya/
ТОЭ. http://ndo.sibsutis.ru/bakalavr/sem3/course110/main.htm
Это единственный из методов формирования ММС, который позволяет получить математическую модель в нормальной форме Коши. Рассмотрим получение ММС на примере механической системы (рис.1)
Рис.1
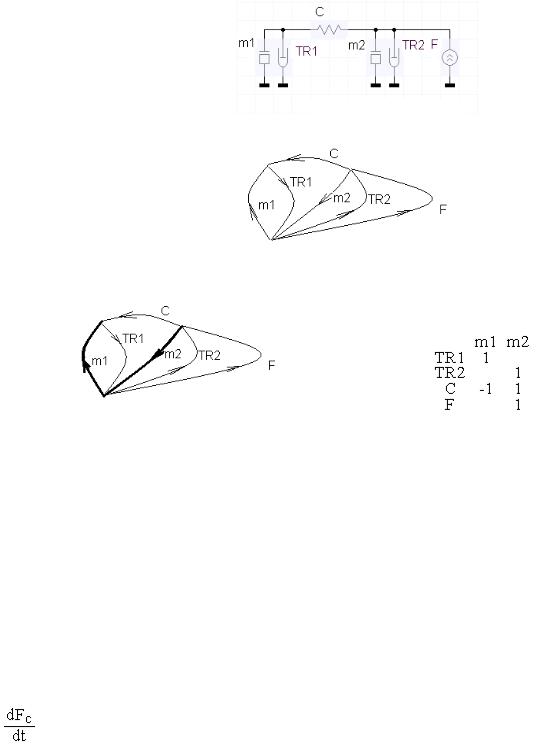
1. Составляем эквивалентную схему (рис.2).
Рис. 2.
2. Строим граф эквивалентной схемы (рис.3) Граф практически повторяет эквивалентную схему, но без условных изображений ветвей.
Рис. 3.
3. Выбираем нормальное дерево графа. Нормальное дерево — это фундаментальное дерево (не образующее контуров), в которое ветви включены согласно приоритету E,C,R,L,I (в соответствии с аналогиями физических однородных подсистем). В данном случае в качестве ветвей дерева нужно использовать ветви m1 и m2. (рис.4)
Рис. 4.
4.Строим матрицу контуров и сечений, где столбцы соответствуют ветвям дерева, а строки — хордам.
5.Для получения топологических уравнений сканируем М-матрицу по строкам и столбцам. При сканировании по строкам получаем уравнения непрерывности (неразрывности), при сканировании по столбцам - уравнения равновесия. При получении уравнений непрерывности знаки элементов матрицы меняются на противоположный (сумма равна 0).
VTR1=-Vm1 VTR2=-Vm2
Vc=Vm1-Vm2 VF=-Vm2
Fm1=FTR1-Fc
Fm2=FTR2+Fc+F
6. Добавляем компонентные уравнения всех ветвей.
FTR1= КTR1VTR1
FTR2= КTR2VTR2
 =
= 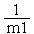 Fm1
Fm1
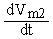 =
= 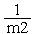 Fm2
Fm2
=CVc
7. Получаем нормальную форму Коши, раскрывая правые части последних трех уравнений
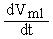 =
=  (FTR1-Fc)=
(FTR1-Fc)= 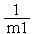 ( КTR1VTR1-Fc)=
( КTR1VTR1-Fc)= 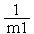 ( КTR1(-Vm1)-Fc)
( КTR1(-Vm1)-Fc)
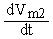 =
= 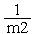 (FTR2+Fc+F)=
(FTR2+Fc+F)= 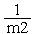 ( КTR2VTR2+Fc+F)=
( КTR2VTR2+Fc+F)= 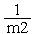 ( КTR2(-Vm2)+Fc+F)
( КTR2(-Vm2)+Fc+F)
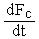 =C(Vm1-Vm2)
=C(Vm1-Vm2)
Далее, используя численный метод интегрирования, решаем систему и получаем переходные процессы.
Примечание 1. Нормальная форма Коши не может быть получена, если в ветви дерева попадет ветвь типа L или в хорды - ветвь типа C. В ряде случаев "особых" систем линейных алгебраических уравнений малые изменения параметров приводят к чрезвычайно большим изменениям в решении этих уравнений, поэтому приведение математических моделей к форме Коши нежелательно для автопилотов, задач устойчивости сооружений и т.п., где ошибки в высших порядках округлений расчетов могут привести к катастрофам.
Узловой метод получения ММС
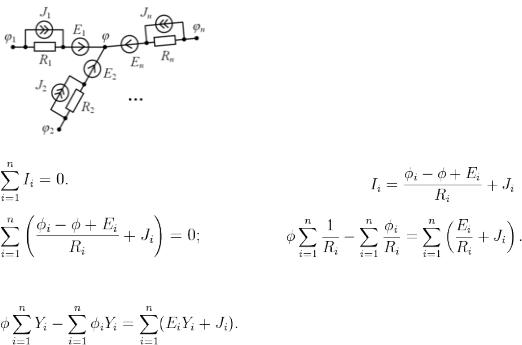
Метод развивался в домашинное время в электротехнике как метод узловых потенциалов и в строительной механике как метод перемещений. Метод узловых потенциалов не привносит ничего нового к правилам Кирхгофа и закону Ома. Он лишь формализует их использование настолько, чтобы их можно было применить к любой сколь угодно сложной цепи и пригоден для расчёта посредством компьютеров. Исходная информация вводится в виде эквивалентной схемы.
Если в цепи, состоящей из У узлов и Р рёбер, известны все характеристики звеньев (полные сопротивления R, величины источников ЭДС E и тока J), то возможно вычислить токи Ii во всех рёбрах и потенциалы φi во всех узлах на основе законов Кирхгофа. Перед началом расчёта выбирается один из узлов (базовый узел), потенциал которого считается равным нулю. Затем узлы нумеруются, после чего составляется система уравнений для каждого узла, кроме базового. При расчёте цепи имеем У-1+Р неизвестных переменных: У–1 узловых потенциалов и Р токов в рёбрах.
Рис. 1. Фрагмент цепи: узел с примыкающими звеньями Согласно 1-му закону Кирхгофа сумма токов в узле равна нулю:
Ток в звене определим, исходя из закона Ома для участка цепи: |
откуда |
или
Обозначив проводимости рёбер через  получим окончательное уравнение для узла
получим окончательное уравнение для узла
При формализации слева от знака равенства записывается потенциал рассматриваемого узла, умноженный на сумму
проводимостей ветвей, примыкающих к нему, минус потенциалы узлов, примыкающих к данному, умноженные на проводимости ветвей, соединяющих их с данным узлом.
Справа от знака равенства записывается сумма всех источников токов, примыкающих к данному узлу, плюс сумма произведений всех ЭДС, примыкающих к данному узлу, умноженная на проводимость соответствующего звена.
Последнее уравнение получено, исходя из предположения, что все источники тока и ЭДС направлены в сторону рассматриваемого узла. Если какой-либо источник направлен в противоположную сторону, его ЭДС или ток необходимо взять с обратным знаком.
В общем виде:
А). Составляется матрица инцидентности А=(aij), которая содержит информацию о структуре схемы (что с чем соединено).
Если i – номер узла, j – номер ветви, aij =(+\-)1, если узел i и ветвь j инцидентны. Иначе 0.
|
|
|
|
|
|
(+) если в ветви направление тока к узлу, (-) если направление тока от узла. |
||
Пример: |
|
|
|
|
|
|
|
|
R1 |
|
|
R2 |
|
R3 |
|
|
|
Ист. тока |
С1 |
|
L1 |
|
|
C2 |
|
|
|
|
|
|
|
|
|
Эквивалентная схема |
|
Матрица инцидентности А : |
|
|
|
|
|
|||
Узлы |
|
C1 |
C2 |
R1 |
R2 |
R3 |
L1 |
J |
1 |
|
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
2 |
|
-1 |
0 |
+1 |
-1 |
0 |
0 |
0 |
3 |
|
0 |
0 |
0 |
+1 |
-1 +1 |
0 |
|
4 |
|
0 |
-1 |
0 |
0 |
+1 |
0 |
0 |
Б). Составляется матрица проводимости ветвей y = dI/dU: |
||||||||
-резистивная ветвь yi =1/Ri |
|
|
|
|
|
|||
-источник тока |
yi |
= 0 |
|
|
|
|
|
|
-емкостная ветвь |
Iс |
= С dU/dt. |
Производим замену производных конечными разностями |
|||||
|
In = C (Un –Un-1)/h , h – шаг интегрирования. In = y Un + q , где y = c/h , q = - c/h Un-1 . |
|||||||
-индуктивная ветвь Un = L (In – In-1)/ h, |
In |
= y Un + q , где y = h/L, q = In-1 |
||||||
В общем виде |
I = Y U + Q - набор компонентных уравнений, где Q – набор известных параметров на предыдущем шаге |
|||||||
интегрирования. |
|
|
|
|
|
|
|
|
В развернутом виде: |
|
|
|
|
|
|
|
|
|
Uc1 |
Uc2 |
UR1 UR2 |
UR3 UL1 UJ1 |
||||
IC1 |
C1/h |
|
|
|
|
|
-C1/h U1n-1 |
|
IC2 |
|
C2/h |
|
|
-C2/h U2n-1 |
|
|
IR1 |
|
1/R1 |
|
|
1/R1 U1 |
|
|
IR2 |
|
1/R2 |
|
|
1/R2 U2 |
|
|
IR3 |
|
|
1/R3 |
|
1/R3 U3 |
|
|
IL1 |
|
|
h/L1 |
h/L1Un-13 |
|
|
|
IJ1 |
K |
|
|
0 |
0 |
|
|
|
матрица узловых проводимостей Y |
вектор невязок Q |
|
|
|||
Y – матрица узловых проводомостей Q – вектор невязок |
|
|
|||||
В). Записываем топологические уравнения в матричной форме: сумма токов каждого узла равна 0. |
|
||||||
|
|
A I = 0 |
|
|
|
|
|
Подставляем вместо тока его значение из матричной формы компонентных уравнений |
|
||||||
|
|
A Y U + A Q |
= 0 |
|
|
||
Переходим от напряжений к потенциалам: любой элемент вектора U есть разность потенциалов инцидентных узлов, что м.б. |
|||||||
выражено в матричной форме через матрицу инциденций: |
|
|
|||||
|
|
U |
= Aт Фи(фи1, фи2, …) |
|
|
||
|
|
A Y Aт |
Фи = A Q |
|
|
||
|
|
или |
Я |
Фи = |
A Q - получена система ММС в виде САУ, |
(1) |
|
|
|
где Я – матрица Якоби (матрица узловых проводимостей Я = dI/ dФи). |
|||||
Для решения этой системы представим ее в виде |
|
|
|
||||
|
где |
-матрица Якоби , |
— вектор правых частей. |
(2) |
|
||
Представим СНАУ в виде |
|
Разлагая |
в ряд Тейлора в окрестностях некоторой точки |
, |
|||
получаем |
|
|
|
|
|
|
|
Сохраняя только линейные члены, получаем СЛАУ с неизвестным вектором |
: |
|
|||||
|
|
|
|
|
|
|
(3) |
|
|
где |
|
— матрица Якоби. |
|
|
|
Решение системы (3) дает очередное приближение к корню системы (2), которое удобно обозначить  .
.
Вычислительный процесс стартует с начального приближения 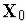 и, в случае сходимости итераций, заканчивается,
и, в случае сходимости итераций, заканчивается,
когда погрешность, оцениваемая как |
станет меньше допустимой погрешности . |
Ограничения классического узлового метода:
-в схемах не должно источников напряжения
-в аргументах зависимых ветвей могут быть только потенциалы
Впрограммах анализа, использующих модифицированный узловой метод, эти ограничения сняты за счет усложнения СЛАУ. Модифицированный узловой метод лежит в основе блоков анализа эквивалентных схем программ PA-9, OrCad, МicroSim, Adams.
Алгоритм анализа на макроуровне включает в себя:
а) получение информации о соединении элементов в узлы на основе эквивалентной схемы или в программно-логистической форме (VHDL, Verilog). Вводимые данные преобразуются во внутреннее представление с помощью графического и лингвистического препроцессоров, в которых предусмотрена диагностика эквивалентной схемы и нарушений формальных языковых правил.
б) алгоритм получения MMC на основе компонентных и топологических уравнений, М-матрицы или матрицы инциденций, узлового метода в) решение полученной СОДУ:
-при помощи дискретизации и алгебраизиции получается СНАУ, которая решается методами прямой итерации (Зейделя), при помощи неявного метода Эйлера или комбинацией явного и неявного методов Эйлера (метод трапеций). Для них необходимо выполнение довольно жестких условий сходимости, характерна сравнительно медленная сходимость.
-при помощи линеаризации (метод Ньютона, разложение в ряд Тейлора) СНАУ заменяется СЛАУ в окрестности некоторой точки
(программно изменяется шаг в окрестности этой точки).
Граф-схема вычислительного процесса при анализе во временной области на макроуровне представлена на рис. Рис. Граф-схема вычислительного процесса при анализе во временной области на макроуровне.

Алгоритм отражает решение системы алгебро-дифференциальных уравнений
На каждом шаге численного интегрирования решается система нелинейных алгебраических уравнений
методом Ньютона.
На каждой итерации выполняется решение системы линейных алгебраических уравнений
Другие используемые обозначения:
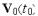 — начальные условия;
— начальные условия;
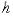 и
и 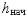 — шаг интегрирования и его начальное значение;
— шаг интегрирования и его начальное значение;
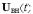 — вектор внешних воздействий;
— вектор внешних воздействий;
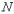 и
и 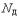 — число ньютоновских итераций и его максимально допустимое значение;
— число ньютоновских итераций и его максимально допустимое значение;
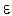 — предельно допустимая погрешность решения СНАУ;
— предельно допустимая погрешность решения СНАУ;
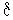 — погрешность, допущенная на одном шаге интегрирования;
— погрешность, допущенная на одном шаге интегрирования;
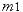 — максимально допустимое значение погрешности интегрирования на одном шаге;
— максимально допустимое значение погрешности интегрирования на одном шаге;
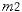 — нижняя граница коридора рациональных погрешностей интегрирования.
— нижняя граница коридора рациональных погрешностей интегрирования.
Из рисунка ясно, что при 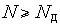 фиксируется несходимость ньютоновских итераций и после дробления шага происходит возврат к интегрированию при тех же начальных для данного шага условиях. При сходимости рассчитывается
фиксируется несходимость ньютоновских итераций и после дробления шага происходит возврат к интегрированию при тех же начальных для данного шага условиях. При сходимости рассчитывается 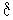 и в зависимости от того, выходит погрешность за пределы диапазона
и в зависимости от того, выходит погрешность за пределы диапазона 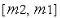 или нет, шаг изменяется либо сохраняет свое прежнее значение. Параметры
или нет, шаг изменяется либо сохраняет свое прежнее значение. Параметры  задаются "по умолчанию" и могут настраиваться пользователем.
задаются "по умолчанию" и могут настраиваться пользователем.
Матрицу Якоби  и вектор правых частей
и вектор правых частей 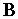 необходимо рассчитывать по программе, составляемой для каждого нового исследуемого объекта. Составление программы выполняет компилятор, входящий в cостав программно-методического комплекса. Общая структура такого комплекса представлена на рис.
необходимо рассчитывать по программе, составляемой для каждого нового исследуемого объекта. Составление программы выполняет компилятор, входящий в cостав программно-методического комплекса. Общая структура такого комплекса представлена на рис.
Анализ процессов в проектируемых объектах можно производить во временной и частотной областях.
Анализ во временной области (динамический анализ) позволяет получить картину переходных процессов, оценить динамические свойства объекта, он является важной процедурой при исследовании как линейных, так и нелинейных систем. Методы анализа во временной области, используемые в универсальных программах анализа в САПР — это численные методы интегрирования систем обыкновенных дифференциальных уравнений (СОДУ), методы алгебраизации. Формулы интегрирования СОДУ могут входить в математическую модель (ММ) независимо от компонентных уравнений или быть интегрированными в ММ компонентов, как это выполнено в узловом методе.
От выбора метода решения СОДУ существенно зависят такие характеристики анализа, как точность и вычислительная эффективность. Эти характеристики определяются прежде всего типом и порядком выбранного метода интегрирования СОДУ. Применяют два типа методов интегрирования — явные методы (иначе экстраполяционные или методы, основанные на формулах интегрирования вперед), и неявные (интерполяционные, основанные на формулах интегрирования назад). Различия между ними удобно показать на примере простейших методов первого порядка — методов Эйлера.
Формула явного метода Эйлера представляет собой следующую формулу замены производных в точке tn

В формуле неявного метода Эйлера использовано дифференцирование назад:
Доказано, что неявные методы более трудоемкие, но и более универсальные в связи с большей устойчивостью (погрешность интегрирования остается ограниченной при любом шаге). Выбор порядка метода решения СОДУ довольно прост:
во-первых, более высокий порядок обеспечивает более высокую точность
во-вторых, среди неявных разностных методов, кроме метода Эйлера, A-устойчивы также методы второго порядка и среди них — метод трапеций. Поэтому преобладающее распространение в программах анализа получили методы второго порядка — модификации метода трапеций (комбинация явного и неявного методов Эйлера).
Анализ в частотной области более специфичен по сравнению с анализом во временной области. Анализ в частотной области выполняется по отношению к линеаризованным моделям объектов. Для линейных систем дифференциальных уравнений справедливо применение для алгебраизации дифференциальных уравнений преобразования Фурье, в котором оператор
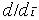 заменяется на оператор
заменяется на оператор 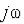 . Особенностью получающейся систем линейных алгебраических уравнений (СЛАУ) является комплексный характер матрицы коэффициентов, что усложняет процедуру решения, но не создает принципиальных трудностей.
. Особенностью получающейся систем линейных алгебраических уравнений (СЛАУ) является комплексный характер матрицы коэффициентов, что усложняет процедуру решения, но не создает принципиальных трудностей.
При решении задают ряд частот 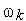 . Для каждой частоты решают СЛАУ и определяют действительные и мнимые части искомых фазовых переменных. По ним определяют амплитуду и фазовый угол каждой спектральной составляющей, что и
. Для каждой частоты решают СЛАУ и определяют действительные и мнимые части искомых фазовых переменных. По ним определяют амплитуду и фазовый угол каждой спектральной составляющей, что и
позволяет построить амплитудно-частотные, фазочастотные характеристики, найти собственные частоты колебательной системы и т.п.
Методы моделирования РЭС в частотной области можно разбить на две группы: в первой из них используется связь между временными и частотными характеристиками цепей, во второй – выполняется непосредственное моделирование выходных параметров радиотехнических устройств.
При спектральном методе анализа переходных процессов пользуются комплексными характеристиками цепи - комплексной проводимостью Y (ω) , комплексным сопротивлением Z(ω) и комплексным коэффициентом передачи K (ω) . Представляя
сложную э.д.с. через гармонические составляющие, мы пользуемся парой преобразований - прямым преобразованием Фурье, когда находим спектральную функцию
|
|
(ω) = |
∞∫ f (t)e− jωt dt , |
|
||||
S |
(1) |
|||||||
|
|
|
|
−∞ |
|
|||
и обратным преобразованием, когда находим функцию f (t) по ее спектральной функции |
||||||||
f (t) = |
|
1 |
∞∫ |
|
(ω)e− jωt dω . |
|
||
|
S |
(2) |
||||||
|
|
|||||||
|
|
|
2π −∞ |
|
||||
Методы моделирования первой группы заключаются в определении по прямому преобразованию Фурье (1) частотного коэффициента передачи и затем расчете спектров выходных сигналов по заданным входным.
С помощью обратного преобразования Фурье (2) можно найти временные характеристики выходных сигналов. Напряжение на выходе цепи (выходной сигнал):
∞ |
|
uвых (t) = 21π −∫∞Sвх (ω)K (ω)e jωt dω . |
(3) |
В методах второй группы частотные функции цепи непосредственно рассчитываются по внутренним параметрам устройства . |
|
Хвых(jω) = K(jω) Хвх(jω), |
где Хвх(jω) и Хвых(jω) – спектры входного и выходного сигналов. (4) |
В современных САПР в подавляющем большинстве случаев используются методы второй группы, в которых для различных значений рабочих частот вычисляются значения частотных характеристик РЭС, так называемый численный спектральный (или частотный) подход. Большое достоинство частотных методов анализа по сравнению с временными методами – высокое быстродействие, возможность анализа устойчивости. Они наиболее удобны при использовании матриц классической и волновой теории четырехполюсников при моделировании РЭС различного назначения.
Прим. Применение теории четырехполюсников для моделирования РЭС
При частотных методах анализа все двухполюсные элементы, входящие в схему, характеризуются своим комплексным сопротивлением z(jω) = r(ω) + jx(ω) или проводимостью y(jω) = 1/z(jω) = g(ω) + jb(ω), зависящими в общем случае от частоты ω.
Четырехполюсные и многополюсные элементы электрических схем описываются соответствующими матрицами параметров. Все матрицы делятся на две основные группы:
- матрицы классической теории четырехполюсника (сопротивлений (импеданса) -Z, проводимости – Y, передачи - А,
гибридная - Н и др);
- матрицы волновой теории четырехполюсника (матрица рассеяния S и волновая матрица передачи Т).
Элементы и структура матриц рассмотривается на примере четырехполюсника N (см. рис 7.1). Пусть к обоим входам четырехполюсника подключены два независимых источника с активными внутренними сопротивлениями.

Рисунок 7.1 – Напряжения и токи на зажимах
четырехполюсника
На СВЧ используется матрица рассеяния, которая состоит из S-параметров, определяющихся как отношение падающей и отраженной волн на входах многополюсника при заданных режимах на остальных входах.
Например, для транзисторного усилителя, имеющего цепи согласования на входе и выходе в полосе частот и собственную матрицу рассеяния, общая матрица соединения равна сумме матриц рассеяния. Особенностью при этом является то, что усилительные свойства СВЧ-транзистора ухудшаются с увеличением частоты. Поэтому согласующе-трансформирующие цепи должны компенсировать избыточное усиление на низших частотах.
Матрицы классической теории четырехполюсника
В случае применения классической теории фазовыми переменными, полностью описывающими цепь (рис. 1), являются частотные характеристики комплексных токов и напряжений на зажимах четырехполюсника.
Соответствующие элементы матриц связывают эти две пары переменных в виде двух уравнений, поэтому при известных матрицах две из фазовых переменных являются зависимыми, а две – независимыми (источниками).
В зависимости от того, какая пара фазовых переменных выбирается независимой, формируется та или иная матрица классической теории. Всего возможны шесть комбинаций пар зависимых и независимых параметров. Все элементы матриц в общем случае также являются функциями комплексной частоты.
В матрице сопротивлений ( режим холостого хода) Z независимыми считаются токи I1 и I2 на зажимах, поэтому напряжения определяются через токи и матрицу сопротивлений. U = Z I
Для определения матрицы проводимости (короткого замыкания) Y независимыми считаются напряжения U1и U2 на зажимах четырехполюсника, тогда токи равны. Элементы матрицы Y называются y-параметрами и определяются в режиме короткого замыкания того или иного входа. Отметим, что y11≠ 1/z11и т.д., так как эти параметры измеряются в разных режимах, в то же время сами матрицы являются взаимно обратными:
Z = Y–1.
Матрица передачи (цепная матрица). А соответствует передаче сигнала с левого зажима четырехполюсника на правый, соответственно. Независимыми фазовыми переменными считаются выходные напряжение U2и ток I2, Элементы матрицы А называются а-параметрами. Элементы матрицы а11и а22называют коэффициентами передачи соответственно по напряжению в режиме холостого хода и по току в режиме короткого замыкания на втором из зажимов четырехполюсника. Элементы а12 и а21 –
передаточные соответственно сопротивление и проводимость при коротком замыкании и холостом ходе на втором входе. Для взаимного четырехполюсника определитель матрицы А равен единице, det A=1.
Гибридная матрица Н получается, когда независимыми фазовыми переменными считаются ток на входе I1 и напряжение на выходе U2 четырехполюсника, Элементы гибридной матрицы Н называются h- параметрами.
Они определяются в режиме холостого хода на входе и короткого замыкания на выходе четырехполюсника.
Элементами гибридной матрицы Н являются h11и h21 – соответственно входное сопротивление и коэффициент передачи по току в режиме короткого замыкания на выходе, h22и h12– соответственно выходная проводимостьи обратный коэффициент передачи по напряжению в режиме холостого хода на входе четырехполюсника.
Области |
применения |
рассмотренных матриц различны при разном включении отдельных четырехполюсников в |
||
составе общей схемы. Так, матрица сопротивлений удобна при анализе последовательного соединения отдельных |
||||
четырехполюсников: общая матрица Z цепи будет равна сумме матриц Zi отдельных четырехполюсников Z = ∑ Zi. |
||||
Матрица |
проводимости |
используется |
при анализе параллельного соединения отдельных четырехполюсников |
|
с общими напряжениями на их зажимах. Тогда общая матрица Y цепи равна сумме матриц Yi отдельных |
||||
четырехполюсников Y = ∑ Yi.i=1 |
|
|
|
|
Цепная |
матрица удобна при каскадном соединении отдельных четырехполюсников, когда выходные напряжения и ток |
|||
предыдущего четырехполюсника совпадают с |
входным напряжением и током последующего. |
|||
В этом случае |
матрица передачи А каскадного соединения равна |
произведению матриц передачи Аi отдельных |
||
четырехполюсников: A = ∏ Ai |
|
|
|
|
Гибридная |
матрица H удобна при макромоделировании транзисторных каскадов, так как условия определения |
|||
элементов данной матрицы близки к физическим режимам работы транзисторов. Гибридная матрица применяется при смеанном соединении отдельных четырехполюсников: последовательном – по входу, параллельном – по выходу.
