
25. Теорема Чевы.
Три
чевианы ![]() треугольника
треугольника ![]() проходят через одну точку или параллельны
тогда и только тогда, когда
проходят через одну точку или параллельны
тогда и только тогда, когда
![]()
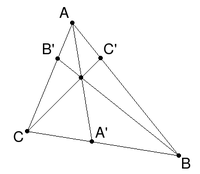
Пусть ![]() лежат
на прямых
лежат
на прямых ![]() треугольника
треугольника ![]() .
Прямые
.
Прямые ![]() параллельны
или пересекаются в одной точке тогда и
только тогда, когда
параллельны
или пересекаются в одной точке тогда и
только тогда, когда
![]()
26.
Если
точки ![]() и
и ![]() лежат
соответственно на сторонах
лежат
соответственно на сторонах ![]() и
и ![]() треугольника
треугольника ![]() или
на их продолжениях[1],
то они коллинеарны тогда
и только тогда, когда
или
на их продолжениях[1],
то они коллинеарны тогда
и только тогда, когда
![]()
где ![]() ,
, ![]() и
и ![]() обозначают отношения
направленных отрезков.
обозначают отношения
направленных отрезков.
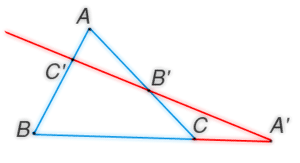
27. Биссектриса угла треугольника —это луч с началом в вершине угла треугольника, делящий угол на два равных угла
Теорема о биссектрисе:
Биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Дк-во:
Дано: ![]() ,
, ![]() —
биссектриса угла
—
биссектриса угла ![]() .
Требуется
доказать:
.
Требуется
доказать: ![]() .
.
Доказательство:
Проведем ![]() до
пересечения с продолжением стороны
до
пересечения с продолжением стороны ![]() .
Стороны угла
.
Стороны угла ![]() пересечены
параллельными прямыми. Составим
пропорцию:
пересечены
параллельными прямыми. Составим
пропорцию: ![]() .
Сравнивая эту пропорцию с той, которую
нужно доказать, замечаем, что они
отличаются только отрезками
.
Сравнивая эту пропорцию с той, которую
нужно доказать, замечаем, что они
отличаются только отрезками ![]() и
и ![]() .
Рассмотрим эти отрезки. Они входят в
.
Рассмотрим эти отрезки. Они входят в ![]() ,
в котором
,
в котором ![]() (как
соответственные при
(как
соответственные при ![]() и
секущей
и
секущей ![]() )
и
)
и ![]() .
Но
.
Но ![]() (
(![]() —
биссектриса), отсюда
—
биссектриса), отсюда ![]() .
Следовательно,
.
Следовательно, ![]() .
Заменим в полученной пропорции
.
Заменим в полученной пропорции ![]() на
на ![]() :
: ![]() .
Теорема доказана
.
Теорема доказана
Доказана.
27(2). . Пропорциональные отрезки — отрезки, для длин которых выполняется пропорция.
Отношением
отрезков AB и CD называется отношение их
длин, то есть![]()
Обобщенная теорема Фалеса:
Если
параллельные прямые, пересекающиеся
двумя данными прямыми, пересекаются с
первой прямой в точках А, В, С, а со второй
прямой соответственно в точках А1,
В1,
С1,
то ![]()
Дк-во:
Проведем через точку А прямую АС1, параллельную прямой ВD(С1- точка пересечения этой прямой с прямой СD). Тогда треугольник ОАВ подобен треугольнику АСС1 по первому признаку подобия треугольников (угол О= углу САС1, угол ОАВ=углу С). Следовательно, ОА/АС=ОВ/АС1. Так как АС1=ВD, то ОА/ОВ=АС/ВD. Теорема доказана.
28. Отрезок АВ является средним пропорциональным (или средним геометрическим) для отрезков АС и ВС, если:
![]()
Теорема:
Катет прямоугольного треугольника есть среднее пропорциональное или среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу
Дк-во:
Пусть прямой угол в треугольнике-С, катеты АС и ВС. Проведём из вершины прямого угла высоту СМ. Проекции катетов МА и МВ. Рассмотрим треугольники АВС И АМС. Они подобны по двум углам : оба прямые и угол А общий. Запишем отношение сторон АВ/АС= ВС/МС= АС/МА Имеем АС в квадрате= АМ*АВ. ( х - есть среднее пропорциональное между а и в если выполняется а/х= х/в х^2=а*в.) Аналогично для треугольников АВС и ВМС ВС^2=АВ*ВМ.
Теорема:
Высота в прямоугольном треугольнике есть среднее пропорциональное между отрезками гипотенузы.
Дк-во:
Рассмотрим треугольники АСМ и ВСМ. Они оба подобны треугольнику АВС, а значит подобны между собой Запишем отношения сторон ВМ/СМ=СМ/АМ СМ^2=АМ*ВМ.
29. Синусом острого прямого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
sinA= BC/AB
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
cosA= AC/AB
Тангенсом острого прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
tgA=BC/AC
Основное тригонометрическое тождество:
![]()
Дк-во:
Пусть
треугольник АВС прямоугольный
(АВ-гипотенуза). sinA=ВС/АВ (1) cosA=AC/AB (2).
Теперь докажем справедливость основного
тригонометрического тождества:![]() .
Из формул (1) и (2) получаем:
sin^2A+cos^2A=ВС^2/AB^2+AC^2/AB^2=BC^2+AC^2/AB^2. По теореме
Пифагора BC^2+AC^2=AB^2,
.
Из формул (1) и (2) получаем:
sin^2A+cos^2A=ВС^2/AB^2+AC^2/AB^2=BC^2+AC^2/AB^2. По теореме
Пифагора BC^2+AC^2=AB^2,![]() .
.
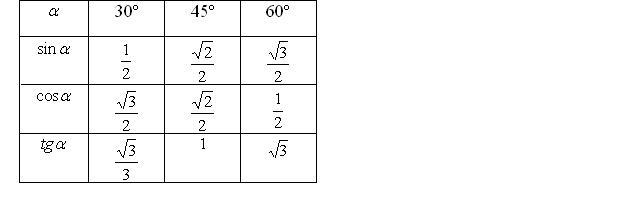
30.
31. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Теорема:
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Дк-во:
Пусть р-касательная к окружности с центром О. А- точка касания. Докажем, что касательная р перпендикулярна к радиусу ОА. Предположим, что это не так. Тогда радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведенный из точки О к прямой р, меньше наклонной ОА, то расстояние от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки. Но это противоречит условию: прямая р- касательная. Таким образом, прямая р перпендикулярна радиусу.
32. . Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
Теорема:
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Дк-во:
Из условия теоремы следует, что данный радиус является перпендикуляром, проведенным из центра окружности к данной прямой. Поэтому расстояние от центра окружности до прямой равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку. Но это и означает, что данная прямая является касательной к окружности. Теорема доказана.
33. Угол с вершиной в центре окружности называется ее центральнм углом.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Дк-во:
Пусть /_ АВС- вписанный угол окружности с центром О, опирающийся на дугу АС. Докажем, что /_ АВС= ½ дуги АС. Решение. Луч ВО совпадает с одной из сторон угла АВС, например со стороной ВС. В этом случае дуга АС меньше полуокружности, поэтому /_ АОС=дугеАС. Так как угол АОС- внешний угол равнобедренного треугольника АВО, а углы ОВА и ВАО при основании р/б треугольника равны, то /_АОС= /_ОВА+/_ВАО=2/_ОВА. Отсюда следует, что 2/_ОВА=дугеАС или /_АВС=/_ОВА=1/2дугиАС. Теорема доказана.
34. Угол с вершиной в центре окружности называется ее центральнм углом.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Следствия из теоремы о вписанном угле:
Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол, опирающийся на полуокружность(диаметр)- прямой.
35. Угол с вершиной в центре окружности называется ее центральнм углом.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Теорема о произведении отрезков двух хорд:
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Дк-во:
Пусть хорды АВ и СD пересекаются в точке Е. Докажем, что АЕ*ВЕ=СЕ*DE. Рассмотрим треугольники АDE и СВЕ. В этих треугольниках углы ЕАD и ЕСВ равны, так как они опираются на одну и ту же дугу ВD, а углы АЕD и СЕВ равны как вертикальные. По первому признаку подобия треугольников, треугольник ADE~ треугольнику СВЕ. Отсюда следует, что АЕ/СЕ=DE/BE, или АЕ*ВЕ=СЕ*DE. Теорема доказана.
