Геометрия. Дополнительные вопросы.

1. Многоуго́льник — это геометрическая фигура, представляющая собой замкнутую ломаную линию.

Многоугольник называется выпуклым,если он лежит по одну сторону от каждой прямой, проходящей через две его соседие вершины.

Сумма внутренних углов n-угольника равна (n − 2)*180. (п. 39-40)

2. Параллелограмм  - четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых.

Свойства параллелограмма:

-Противоположные стороны параллелограмма равны. -Противоположные углы параллелограмма равны . -Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Признаки параллелограмма: -Противоположные стороны попарно равны и параллельны.

-Противоположные углы попарно равны.

-Диагонали делятся в точке их пересечения пополам.

3.

Теорема Фалеса

Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. Справедливо и более общее утверждение, называемое обобщенной теоремой Фалеса: отрезки, высекаемые параллельными прямыми на одной прямой, пропорциональны отрезкам на другой прямой.

4.Треуго́льник (в евклидовом пространстве) — этогеометрическаяфигура, которая состоит из трёх точек, не лежащих на однойпрямой

Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника.

Теорема:

  Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.           Дано: DE — средняя линия треугольника ABC. 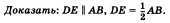          Доказательство. Проведем через точку D прямую, параллельную стороне АВ. По теореме Фалеса она пересекает отрезок АС в его середине, т. е. содержит среднюю линию DE. Значит, средняя линия DE параллельна стороне АВ (рис. 53).           Проведем теперь среднюю линию DF. Она параллельна стороне АС. Четырехугольник AEDF — параллелограмм. По свойству параллелограмма ED = — AF, а так как AF = FB по теореме Фалеса, то ED = АВ. Теорема доказана.(п62)

5. Трапеция- это четырехугольник у которого две стороны параллельны, а другие нет.

Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной.

Трапеция, имеющая прямыеуглы при боковой стороне, называетсяпрямоугольной.

Св-ва р/б трапеции:

• Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.

• В равнобедренной трапеции углы при любом основании равны.

• В равнобедренной трапеции длины диагоналей равны.

• Если трапецию можно вписать в окружность, то она равнобедренная.

• Около равнобедренной трапеции можно описатьокружность.

• Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

6. Трапеция- это четырехугольник у которого две стороны параллельны, а другие нет.

Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон этой фигуры.

   Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.           Пример.           

7. Теорема Вариньона:

Середины сторон произвольного четырёхугольника — вершины параллелограмма

8. Прямоугольник- параллелограмм у которого все углы прямые.

Особое св-во:

Диогонали прямоугольника равны.

Признак:

Если в параллелограмме диагонали равны, то этот парралелограмм- прямоугольник.

9. Ромб – это параллелограмм у которого все стороны равны.

Cв-во:

Диагонали ромба взаимно перпендикулярны, и делят его углы пополам.

Квадрат – это прямоугольник у которого все стороны равны.

10. Св-ва площадей мн-ков:

-Равные мн-ки имеют равные площади

-Если мн-ник составлен из нескольких мн-ков, то его полщадь будет равна сумме площадей этих мн-ков.

-Площадь квадрата равна квадрату его стороны.

Теорема о площади прямоугольника.

Площадь прямоугольника равна произведению его смежных сторон.

11. Св-ва площадей мн-ков:

-Равные мн-ки имеют равные площади

-Если мн-ник составлен из нескольких мн-ков, то его полщадь будет равна сумме площадей этих мн-ков.

-Площадь квадрата равна квадрату его стороны.

Теорема о площади параллелограмма:

Площадь параллелограмма равна произведению его основания на высоту.

Теорема о площади треугольника:

Площадь треугольника равна половине произведения его основания на высоту.

Следствие 1:

Площадь прямоугольного треугольника равна половине произведения его катетов.

Следствие 2:

Если высоты двух треугольников равны, то их площади относятся как основания.

Теорема о площади трапеции:

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

12. Следствие 1:

Площадь прямоугольного треугольника равна половине произведения его катетов.

Следствие 2:

Если высоты двух треугольников равны, то их площади относятся как основания.

13. Теорема:

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

Теорема:

Если высоты двух треугольников равны , то их площади относятся как основания.

Теорема.

Если основания двух треугольников равны, то их площади относятся как высоты.

14. . Св-ва площадей мн-ков:

-Равные мн-ки имеют равные площади

-Если мн-ник составлен из нескольких мн-ков, то его полщадь будет равна сумме площадей этих мн-ков.

-Площадь квадрата равна квадрату его стороны.

Теорема:

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Геометрия. Основные вопросы.

15. Теорема Пифагора.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Д-во:

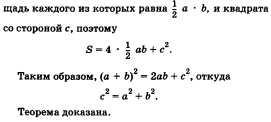
Обратная теорема Пифагора:

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

16.

Дк-во:

 

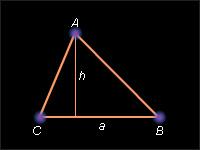
Доказательство

Пусть ABC – данный треугольник. Дополним его до параллелограмма ABCD , как показано на рисунке.

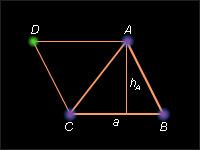
Площадь параллелограмма равна сумме площадей треугольников ABC и CDA . Так как эти треугольники равны, то площадь параллелограмма равна удвоенной площади треугольника ABC . Высота параллелограмма, соответствующая стороне CB , равна высоте треугольника, проведенной к стороне CB . Отсюда следует утверждение теоремы, и 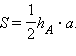Теорема доказана.

17. Пропорциональные отрезки — отрезки, для длин которых выполняется пропорция.

Отношением отрезков AB и CD называется отношение их длин, то есть

 Подобные треугольники — треугольники, у которых углы соответственно равны, и стороны одного пропорциональны сходственным сторонам другого треугольника.

Первый признак подобия треугольников:

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.

То есть ∆ABC ~ ∆A₁B₁C₁ <=> ∠A=∠A₁, ∠B=∠B₁.

Дк-во:

18. . Пропорциональные отрезки — отрезки, для длин которых выполняется пропорция.

Отношением отрезков AB и CD называется отношение их длин, то есть

 Подобные треугольники — треугольники, у которых углы соответственно равны, и стороны одного пропорциональны сходственным сторонам другого треугольника.

Второй признак подобия треугольников:

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то треугольники подобны.

Дк-во:

Доказательство

Пусть у треугольников ABC и иДокажем, чтоПереведем треугольник A₁ B ₁ C ₁гомотетией f с любым центром и коэффициентом k в треугольник A ₂ B ₂ C ₂. Δ A ₂ B ₂ C ₂  = Δ ABC . Действительно, Треугольникии ABC равны по первому признаку равенства треугольников (теорема 4.1). По теореме 12.6 существует движение g , переводящее Δ A₂ B ₂ C ₂ в Δ ABC . Выполнив сначала гомотетию f , а затем движение g , получим подобие g  ○  f , которое переводит Δ A ₁ B ₁ C ₁ в Δ ABC . Следовательно, Теорема доказана.

19. . Пропорциональные отрезки — отрезки, для длин которых выполняется пропорция.

Отношением отрезков AB и CD называется отношение их длин, то есть

 Подобные треугольники — треугольники, у которых углы соответственно равны, и стороны одного пропорциональны сходственным сторонам другого треугольника.

Третий признак подобия треугольников:

 Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Дк-во:

20. Подобные треугольники — треугольники, у которых углы соответственно равны, и стороны одного пропорциональны сходственным сторонам другого треугольника.

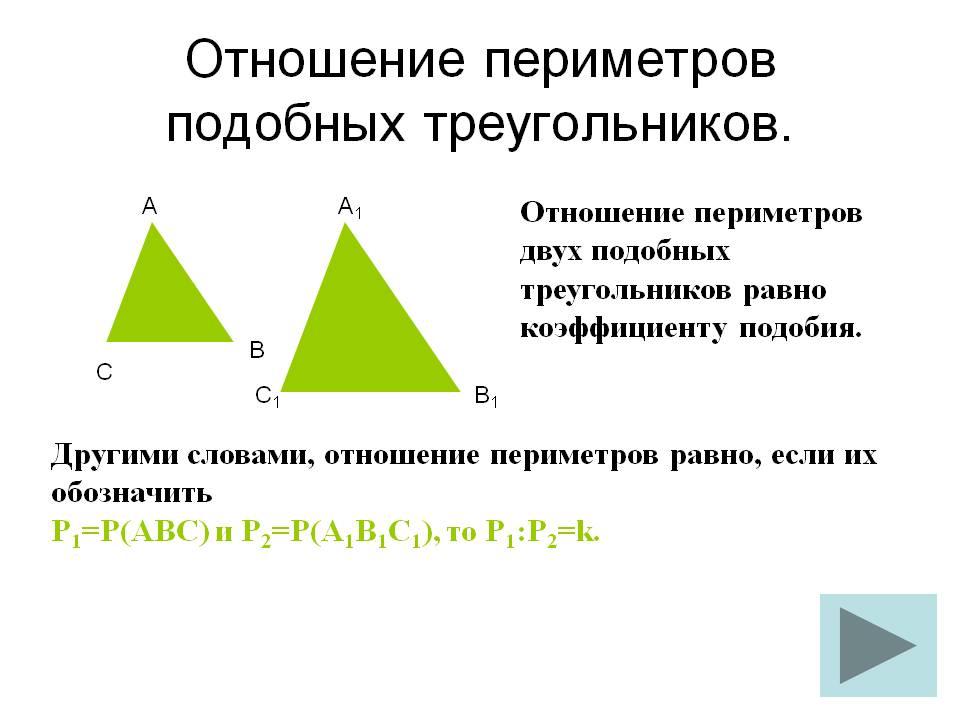
Теорема об отношении площадей подобных треугольников:

Отношение площадей 2 подобных треугольников равно квадрату коэффициента подобия.

Дк-во:

Пусть треугольники ABC и А₁В₁С₁ подобны, причем коэффициент подобия равен k O, обозначим буквами S и S₁ площади этих треугольников. Так как A=A₁, то

S/S₁ = AB*AC/A₁B₁*A₁C₁

(по тереме об отношении площадей треугольника). По формулам имеем: АВ/А₁В₁ = k, AC/A₁C₁ = k

поэтому

S/S₁ = k²

Теорема доказана.

21. Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

-Медиана разбивает треугольник на два треугольника одинаковой площади.

-Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называетсяцентром тяжести треугольника.

-Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника

Замечательные точки треугольника

Замечательные точки треугольника – это неформальное название для точек пересечения его медиан, высот , центров вписанной иописанной окружностей, а также ряда других точек.

22. Биссектриса угла - это луч с началом в вершине угла, делящий угол на две равные части

Теорема о биссектрисе угла:

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Обратная теорема:

Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Следствие:

Биссектрисы треугольника пересекаются в одной точке.

Д-во:

1)Возьмем произвольную точку М на биссектрисе угла ВАС, проведем перпендикуляры MK и ML к прямым АВ и АС и докажем, что MK=ML. Рассмотрим прямоугольные треугольники АМК и AML. Они равны по гипотенузе и острому углу(АМ-общая гипотенуза, угол1=углу2 по условию). Следовательно MK=ML

2) Пусть точка М лежит внутри угла ВАС и равноудалена от его сторон АВ и АС. Докажем, что луч АМ- биссектриса угла ВАС. Проведем перпендикуляры МК и ML к прямым АВ и АС. Прямоугольные треугольники равны АМК и АМL равны по гипотенузе и катету(АМ- общая гипотенуза, MK=ML по усовию). Следовательно, угол 1 = углу 2. Это и означает, то что луч АМ является биссектрисой угла ВАС. Теорема доказана.

Замечательная точка- это точка пересечения биссектрис, высот и медиан.

23. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

Теорема:

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка

Обратная:

Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Дк-во:

Пусть прямая m- серединный перпендикуляр к отрезку АВБ точка О- середина этого отрезка.

1)Рассмотрим произвольную точку М прямой m и докажем, что АМ=ВМ. Если точка М совпадает с точкой О, то это равенство верно, так как О- середина отрезка АВ. Пусть М и О- различные точки. Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам(ОА=ОВ, ОМ- общий катет), поэтому АМ=ВМ.

2) Рассмотри произвольную точку Р, равноудаленную от концов отрезка АВ, и докажем, что точка Р лежит на прямой m. Если Р- точка прямой АВ, то она совпадает с серединой О отрезка АВ и поэтому лежит на прямой m. Если же точка Р не лежит на прямой АВ, то треугольник АРВ равнобедренный, так как АР=ВР. Отрезок РО- медиана этого треугольника, а значит и высота. Следовательно: РО параллельно АВ, поэтому прямые ОР и m совпадают, т.е. Р- точка прямой m. Теорема доказана.

Замечательная точка- это точка пересечения биссектрис, высот и медиан.

24. Высота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону

Теорема:

Высоты треугольника (или их продолжения) пересекаются в одной точке.

Дк-во:

Рассмотрим произвольный треугольник АВС и докажем, что прямые АА1, ВВ1 и СС1, содержащие его высоты, пересекаются в одной точке. Проведем через каждую вершину треугольника АВС прямую, параллельную противоположной стороне. Полчим треугольник А2В2С2. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ=А2С и АВ=СВ2 как противоположные стороны параллелограммов АВА2С и АВСВ2, поэтому А2С =СВ2. Аналогично С2А=АВ2 и С2В=ВА2. Кроме того, как следует из построения, СС1перпендикулярноА2В2, АА1перпендикулярноВ2С2 и ВВ1перпендикулярноА2С2. Таким образом, прямые АА1, ВВ1 и СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2. Следовательно, они пересекаются в одной точке. Теорема доказана.

Замечательная точка- это точка пересечения биссектрис, высот и медиан.