
- •Дифференциальные уравнения
- •2. Дифференциальные уравнения первого порядка.
- •Понятие об изогональных траекториях.
- •7.5. Интегрирование простейших типов д.У. 1-го порядка.
- •7.5.1. Д.У. С разделяющимися переменными.
- •7.5.3. Линейные уравнения 1-го порядка.
- •7.5.5. Д.У. В полных дифференциалах.
- •3. Д.У. 2-го порядка. Интегрирование методом понижения порядка.
- •3.1. Общие положения.
- •9. Линейные д.У..
- •9.1. Введение.
- •9.2.2. Фундаментальная система решений однородного линейного д.У.
- •9.2.3. Формула Остроградского-Лиувилля Пусть и– решения (2), следовательно,
- •9.2.4. Существование фср (2)
- •9.2.5. Применение формулы Остроградского-Лиувилля
- •9.3. Линейные неоднородные дифференциальные уравнения 2-го порядка
- •9.3.1. Теоремы о частных решениях
- •9.3.2. Метод вариации произвольных постоянных для нахождения частного решения неоднородного дифференциального линейного уравнения 2-го порядка
- •9.4. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и приводящиеся к ним
- •9.4.1. Интегрирование однородных линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами
- •9.4.2. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
- •В силу следствия достаточно найти решение уравнения
- •9.4.3. Линейные дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами
- •9.4.4. Линейные дифференциальные уравнения n-го порядка
- •9.5. Системы дифференциальных уравнений
- •9.5.1. …
В силу следствия достаточно найти решение уравнения
![]() ,
,
но последнее было уже рассмотрено. Из этого следует, что его решение нужно искать в виде
![]() ,
,
![]() –с
неопределенными комплексными
коэффициентами,
–с
неопределенными комплексными
коэффициентами,
![]() – кратность
– кратность![]() в характеристическом уравнении.
в характеристическом уравнении.
На основании теоремы о наложении решений и следствия из вспомогательной теоремы,
![]() ,
,
где
![]() сопряжен с
сопряжен с![]() .
.
Снова используем формулы Эйлера:
![]() ,
,
![]() .
.
Приводим
![]() к виду
к виду
![]() , (**)
, (**)
где
![]() ,
,![]() – многочлены с вещественными
коэффициентами.
– многочлены с вещественными
коэффициентами.
Замечание.
При
использовании (**) надо помнить, что вид
![]() подобен виду
подобен виду![]() ,
но является более полным. Так, если
,
но является более полным. Так, если![]() ,
то в (**) мы должны брать
,
то в (**) мы должны брать![]() ,
если
,
если![]() ,
то в (**) следует взять
,
то в (**) следует взять![]() ,
и если
,
и если![]() ,
то в (**) возьмем
,
то в (**) возьмем![]() ,
и т. д.
,
и т. д.
Пример.
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
так как
,
так как![]() не корень характеристического уравнения,
не корень характеристического уравнения,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
и т. д.
,
и т. д.
9.4.3. Линейные дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами
Теорема.
Линейное дифференциальное уравнение преобразуется снова в линейное дифференциальное уравнение при всяком линейном преобразовании неизвестной функции и любом преобразовании аргумента (и только при таких преобразованиях).
Доказательство.
В уравнении
![]()
положим
![]() ,
где
,
где![]() – новая искомая функция, а
– новая искомая функция, а![]() и
и![]() – известные функции. Тогда
– известные функции. Тогда
![]() ,
,
![]() ,
,
и исходное уравнение преобразуется к виду
![]() ,
,
и
это уравнение снова является линейным,
так как все коэффициенты и правая часть
есть функции только
![]() .
отметим, что
.
отметим, что![]() входит только в правую часть.
входит только в правую часть.
Положим,
что
![]() ,
тогда
,
тогда![]() и
и
![]() ,
,![]() .
.
Подставляя эти значения, получим опять линейное уравнение:
![]() ,
,
заменяя
![]() на
на![]() найдем, что все коэффициенты и правая
часть есть функции только
найдем, что все коэффициенты и правая
часть есть функции только![]() .
На этом доказательство первой части
закончено.
.
На этом доказательство первой части
закончено.
Предположим
теперь, что
![]() .
Тогда
.
Тогда
![]() ,
,![]() .
.
Подставляя
![]() ,
,![]() и
и![]() в исходное уравнение, получим в общем
случае нелинейное уравнение
в исходное уравнение, получим в общем
случае нелинейное уравнение
![]() . (*)
. (*)
Чтобы
(*) было линейным, нужно, чтобы
![]() и
и![]() не зависели от
не зависели от![]() ,
,![]() ,
а
,
а![]() содержало
содержало![]() лишь в первой степени или было функцией
только от
лишь в первой степени или было функцией
только от![]() .
Выполнение этих требований превращает
.
Выполнение этих требований превращает![]() в линейную функцию. Если
в линейную функцию. Если
![]()
![]()
![]() ,
,
и
тогда
![]() не зависит от
не зависит от![]() ,
а
,
а![]() .
При этом
.
При этом
![]()
есть
функция от
![]() в первой степени. Таким образом, теорема
доказана.
в первой степени. Таким образом, теорема
доказана.
Очевидно, что для преобразования линейного дифференциального уравнения с переменными коэффициентами в линйое дифференциальное уравнение с постоянными коэффициентами достаточно рассмотреть соответствующее однородное уравнение.
Согласно
теореме, сохранение линейности возможно
только в двух случаях: при линейном
преобразовании функции
![]() (
(![]() ,
так как она не входит в коэффициенты в
левой части) и при произвольном
преобразовании
,
так как она не входит в коэффициенты в
левой части) и при произвольном
преобразовании![]() .
.
Теперь
выведем условия, налагаемые на
![]() и
и![]() линейного дифференциального уравнения
2-го порядка, при которых это уравнение
может быть приведено к линейному
дифференциальному уравнению 2-го порядка
с постоянными коэффициентами с помощью
преобразования
линейного дифференциального уравнения
2-го порядка, при которых это уравнение
может быть приведено к линейному
дифференциальному уравнению 2-го порядка
с постоянными коэффициентами с помощью
преобразования![]() или
или![]() .
.
Необходимое
и достаточное условие
для преобразования
![]() .
.
Итак, пусть дано уравнение
![]() (1)
(1)
и
подстановка
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
подставляя в уравнение, получим:
 , (2)
, (2)
и
потребуем, чтобы коэффициенты при
![]() и
и![]() были константами:
были константами:
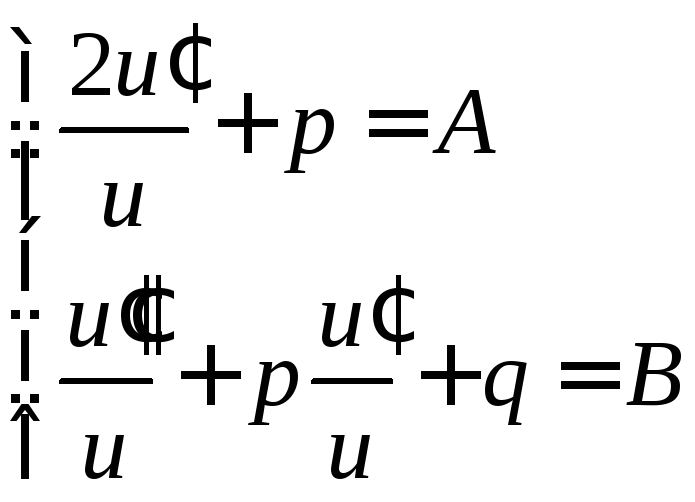 .
.
Тогда
![]() .
Отсюда
.
Отсюда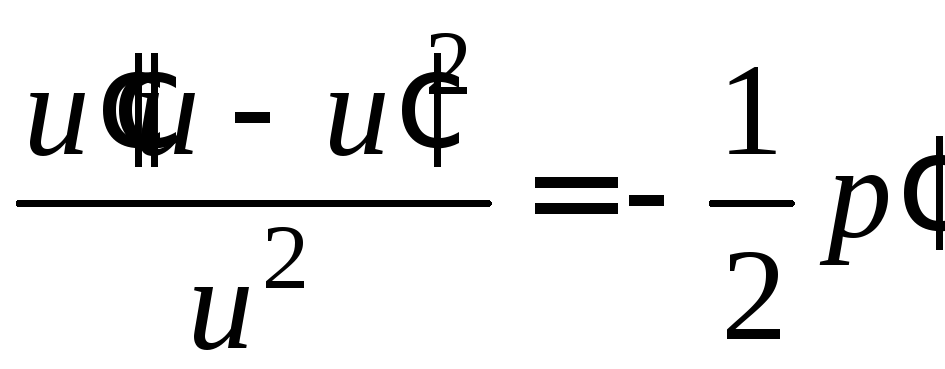 или
или

![]()
 или
или
![]() .
.
Последнее равенство можно записать, как
![]() ,
где
,
где![]() . (3)
. (3)
(3) и есть условие приводимости (1) к (2), в котором коэффициенты являются постоянными.
Найдем
теперь
![]() ,
с помощью которой это приведение
выполняется:
,
с помощью которой это приведение
выполняется:
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Положим
![]() и
и![]() ,
тогда
,
тогда![]() и
и
![]() .
.
Таким образом, преобразование выполняется, если выполнено (3).
Пример.
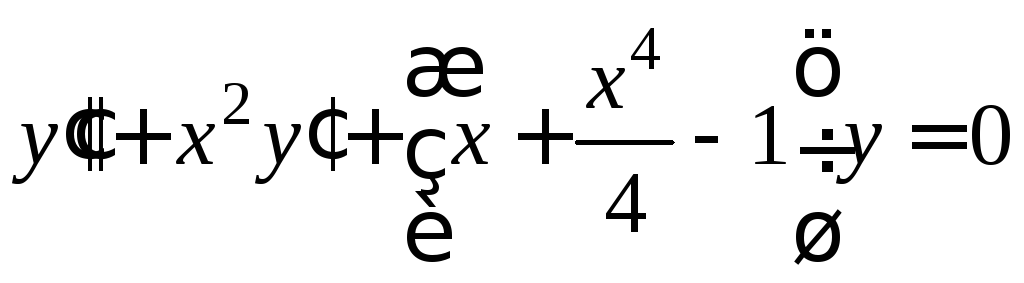 .
.
Условие
(3) выполняется и
![]() приводит к уравнению
приводит к уравнению
![]() .
.
Необходимое
и достаточное условие
для преобразования
![]() .
.
Пусть
![]() ,
тогда
,
тогда
![]() и
и![]()
![]()
 . (
. (![]() )
)
Далее,

![]()
Из
(*), считая
![]() ,
имеем
,
имеем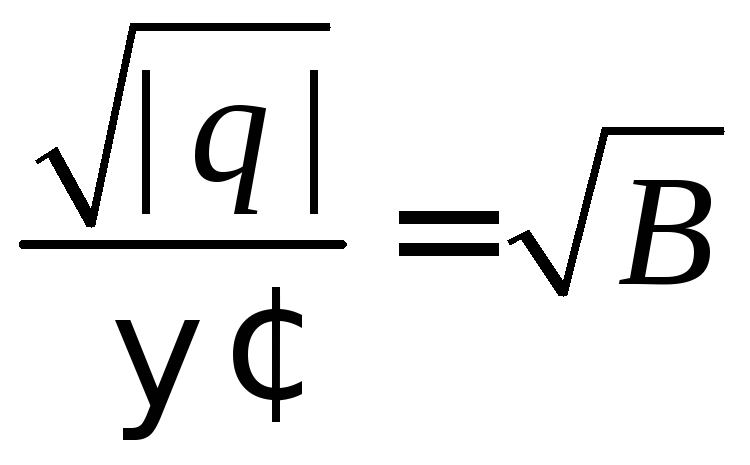
![]()
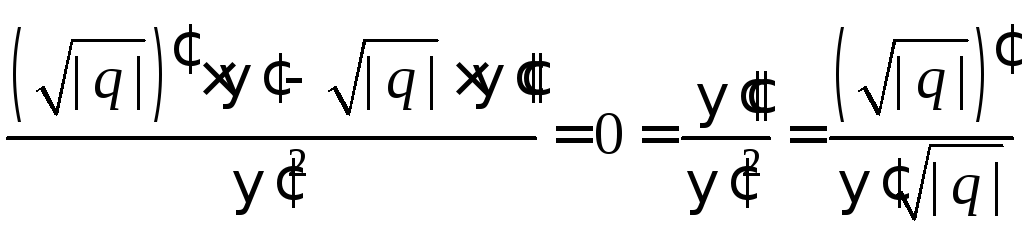 .
.
Кроме
того,
 .
Подставляя эти результаты в (**), получим:
.
Подставляя эти результаты в (**), получим:
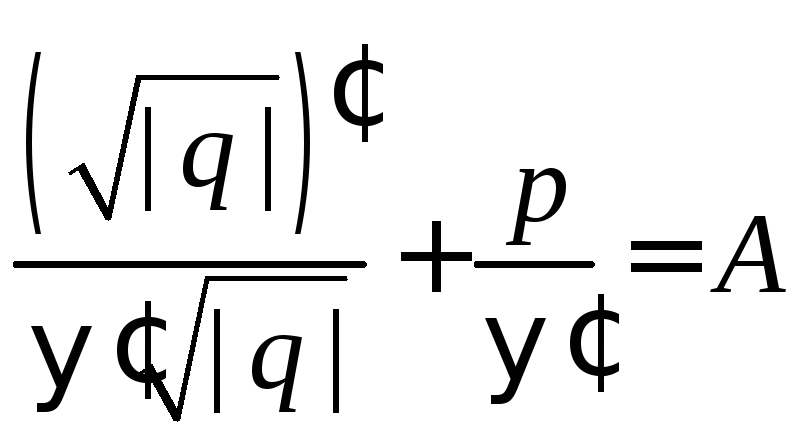 или
или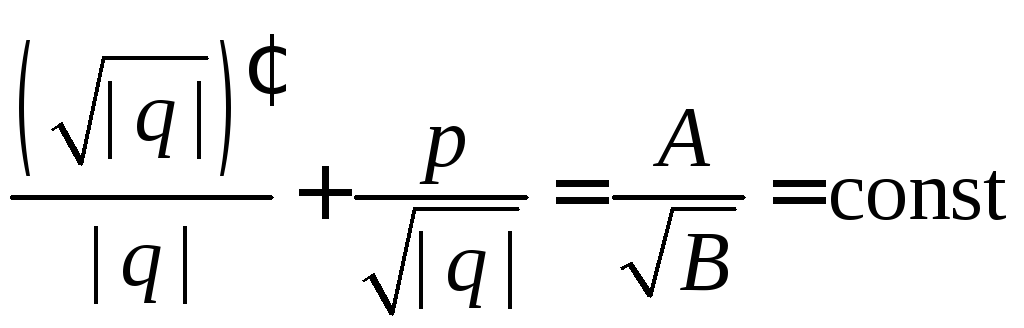 ,
,
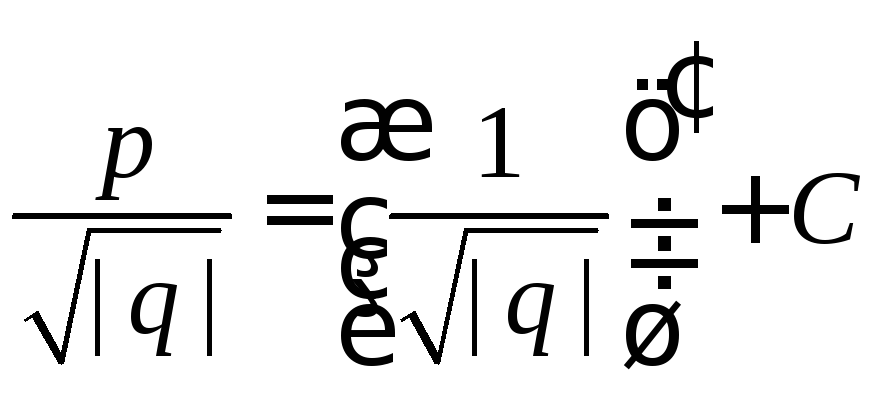 . (
. (![]() )
)
(![]() )
и есть искомое условие.
)
и есть искомое условие.
Найдем
теперь
![]() .
Из (*):
.
Из (*):

![]()
![]()
![]()
![]() ,
,
где
![]() ,
а
,
а![]() – одна из первообразных от
– одна из первообразных от![]() .
.
Таким
образом, если выполняется (![]() ),
то (1) можно привести к уравнению с
постоянными коэффициентами с помощью
преобразования
),
то (1) можно привести к уравнению с
постоянными коэффициентами с помощью
преобразования![]() .
.
Пример. Рассмотрим уравнение Эйлера
![]() ,
,
здесь
![]() ,
,![]() ,
,![]() ,
,![]() –
–![]() ,
тогда
,
тогда![]() или
или![]() – нужная подстановка.
– нужная подстановка.
