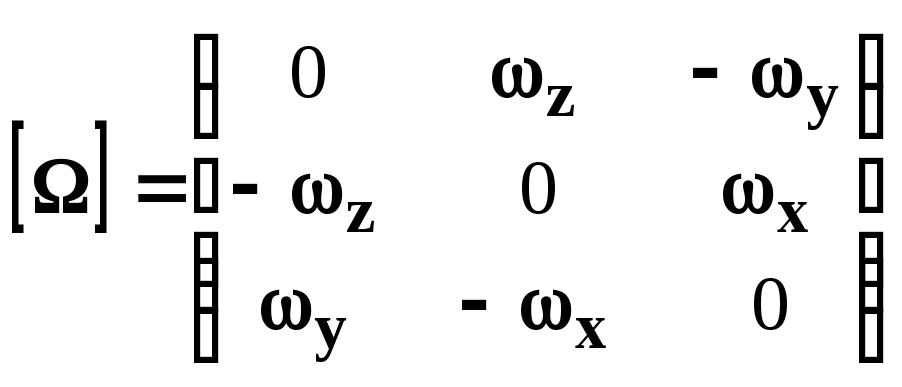Кинематика углового движения ла.
Хотя
движение вокруг ЦМ описывается как
угловое движение связанной СК относительно
нормальной, но для этого движения
уравнения кинематики обычно записывают
также в одной из двух форм - в зависимости
от того, как описывается вращение
связанной СК относительно нормальной
- в виде углов Эйлера
(рыскания, тангажа, крена) или - с помощью
матрицы перехода
![]() (матрицы направляющих косинусов). Т.е.
кинематика углового движения – это
зависимость либо скоростей изменения
углов Эйлера, либо скоростей изменения
матрицы направляющих косинусов от
угловых скоростей по крену, рысканию и
тангажу.
(матрицы направляющих косинусов). Т.е.
кинематика углового движения – это
зависимость либо скоростей изменения
углов Эйлера, либо скоростей изменения
матрицы направляющих косинусов от
угловых скоростей по крену, рысканию и
тангажу.
Следует обратить внимание, что угловые скорости по крену, рысканию и тангажу не совпадают с производными углов Эйлера по времени – угловые скорости по крену, рысканию и тангажу – это проекции вектора угловой скорости вращения связанной системы относительно нормальной на оси связанной системы (ортогональной), а углы Эйлера (следовательно - и их производные) соответствуют поворотам вокруг осей разных систем.
Так как скорости изменения углов Эйлера не образуют прямоугольную систему координат, то для получения кинематических уравнений движения вокруг ЦМ находят выражение угловых скоростей по крену, рысканию и тангажу от скоростей изменения углов Эйлера, а затем решают эту систему уравнений относительно нужных скоростей.
Проецируя на оси связанной СК, получают следующую систему уравнений
![]() ;
;
![]() ;
;
![]() ,
,
а решая ее относительно угловых скоростей крена, рыскания, тангажа, получают нужные уравнения кинематики, называемые уравнениями Эйлера
![]() ;
;
![]() ; (4э)
; (4э)
![]() .
.
Следует заметить, что здесь , но это ограничение заложено уже в самой процедуре перехода с помощью углов Эйлера.
Для получения уравнений кинематики движения вокруг ЦМ с использованием матрицы перехода воспользуемся тем, что строки матрицы перехода от нормальной системы к связанной
Dсвg
=
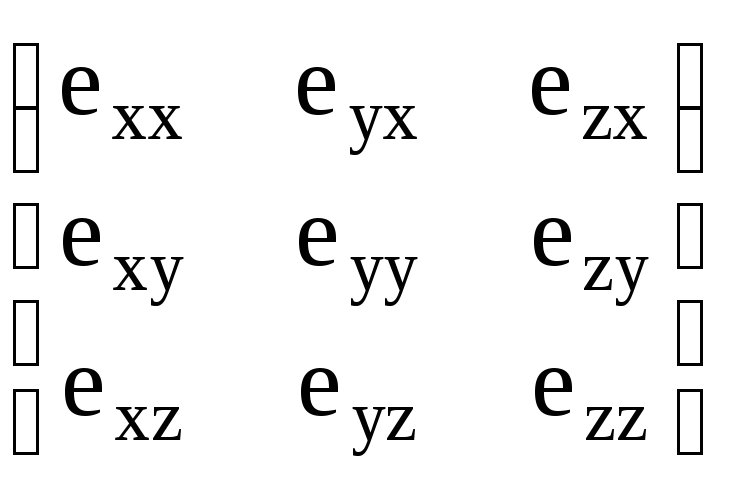
- это проекции ортов (всех трех) нормальной системы на соответствующую ось связанной. Например, первая строка
((exg)x (eyg)x (ezg)x) , или в общепринятых обозначениях (exx eyx ezx) – это проекции ортов exg, eyg, ezg на ось х связанной системы.
Это непосредственно следует из определения матрицы перехода.
Столбцы этой же матрицы – это проекции соответствующего орта нормальной системы на оси связанной, например, первый столбец
((exg)x (exg)y (exg)z)Т, или в общепринятых обозначениях (exx exy exz)Т – это проекции орта exg на оси х,y,z связанной системы (точнее - орт exg, записанный своими проекциями в связанной системе).
Орты нормальной системы неподвижны, т.е. их производные по времени равны нулю. Если взять эти производные в проекциях на оси связанной системы, то по правилам дифференцирования exg’ + exg = 0, где - вектор угловой скорости вращения связанной системы относительно нормальной. Но exg’ – это первый столбец матрицы (Dсвg)’. Аналогично можно найти и остальные столбцы. Полученная таким образом система уравнений называется уравнениями Пуассона
exx'=zexy - yexz
exy'=xexz - zexx
exz'=yexx - xexy
eyx'=zeyy - yeyz (4п)
eyy'=xeyz - zeyx
eyz'=yeyx - xeyy
Последнюю тройку уравнений можно не составлять, так как из свойств матрицы перехода третий столбец можно определить как алгебраические дополнения
ezx=exyeyz - eyyexz
ezy=exzeyx - eyzexx
ezz=exxeyy - eyxexy
Систему дифференциальных уравнений Пуассона можно записать в матричном виде
(Dсвg)’=[]Dсвg,
где
[]
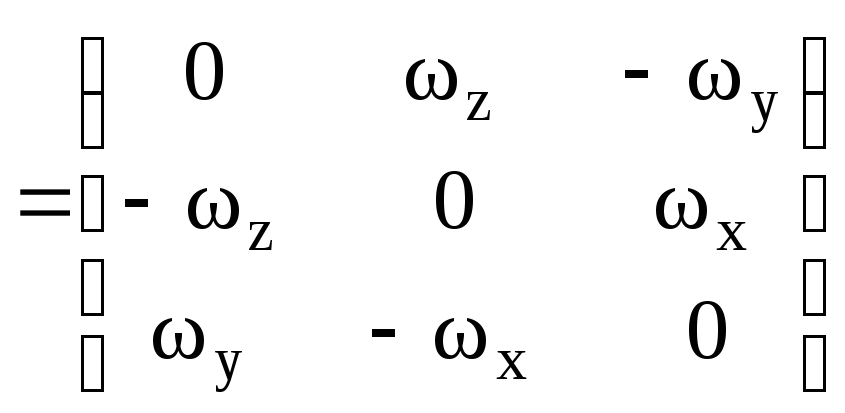 .
.
Последнее соотношение проверяется непосредственно. Очевидно, что (Dgсв)’=Dgсв[]т= Dgсв[-].
Уравнения (1 - 4) образуют полную систему уравнений пространственного движения аэродинамического ЛА. Полученная система уравнений содержит ряд переменных, которые в них не определяются (входящие, например, в силы и моменты). Среди таких переменных есть управляющие i, но есть и параметры движения V, , . Для их определения надо проводить дополнительные вычисления.
Для
определения модуля воздушной скорости
V
достаточно найти проекции воздушной
скорости на оси нормальной системы,
предварительно определив сам вектор
воздушной скорости
![]() ,
где
,
где
![]() -
вектор скорости ветра, но для определения
и
- нужны проекции воздушной скорости на
оси связанной системы. Так как ветер
измеряется в нормальной земной СК, то
в связанной СК
-
вектор скорости ветра, но для определения
и
- нужны проекции воздушной скорости на
оси связанной системы. Так как ветер
измеряется в нормальной земной СК, то
в связанной СК
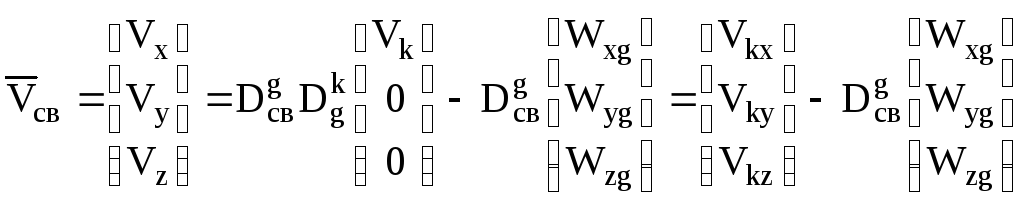 ,
,
![]() ,
,
![]() ,
,
![]() .
.
Еще одна группа дополнительных вычислений – это определение углов Эйлера при описании углового движения в направляющих косинусах и углов пути и наклона траектории при описании движения ЦМ в проекциях траекторной скорости на оси связанной системы.
В заключение приведем пример полной системы уравнений движения с использованием рассмотренных альтернативных вариантов. В этой системе:
- в качестве управляющих воздействий используются отклонения следующих управляющих органов: руль высоты в, элероны э, руль направления н, ручка управления двигателем РУД;
- аэродинамические коэффициенты сил и моментов заданы в связанной СК
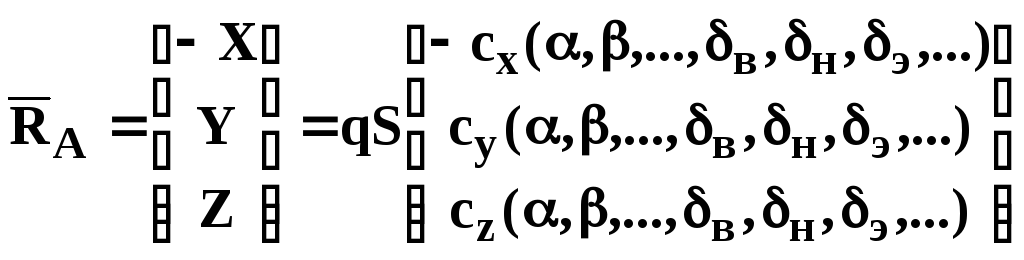 ,
,
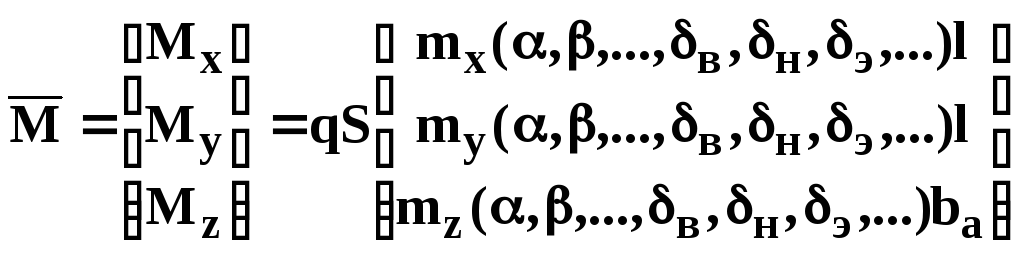 ,
,
![]() -
скоростной напор,
-
скоростной напор,
![]() - плотность воздуха, S
- площадь крыла, l
- размах крыла, bа
- средняя аэродинамическая хорда крыла;
- плотность воздуха, S
- площадь крыла, l
- размах крыла, bа
- средняя аэродинамическая хорда крыла;
-
вектор тяги лежит в плоскости симметрии
ЛА под углом т
к продольной оси, имеет модуль
![]() и точку приложения с координатами xт
и yт;
и точку приложения с координатами xт
и yт;
-
учтены лишь главные центральные моменты
инерции ЛА
![]() ;
;
- учтены гироскопические моменты от вращения турбин двигателя, причем ось этого вращения параллельна оси х, а суммарный момент количества движения обозначен Lдв.
Кинематика поступательного движения:
|
|
или
|
где
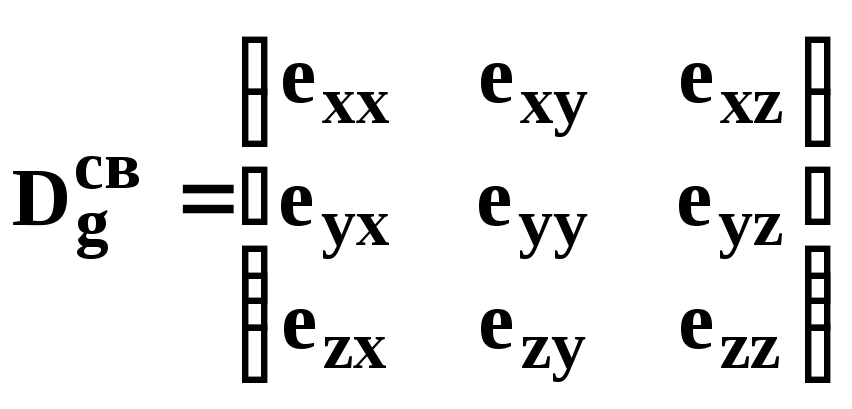 ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Динамика поступательного движения:
 в траекторной
СК в связанной СК
в траекторной
СК в связанной СК
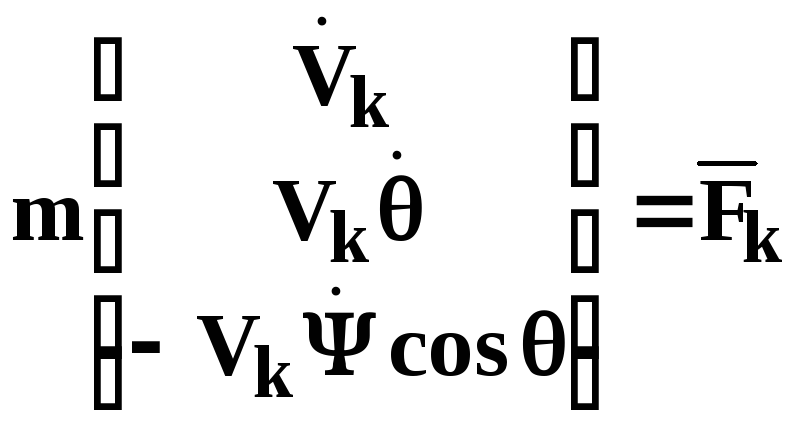
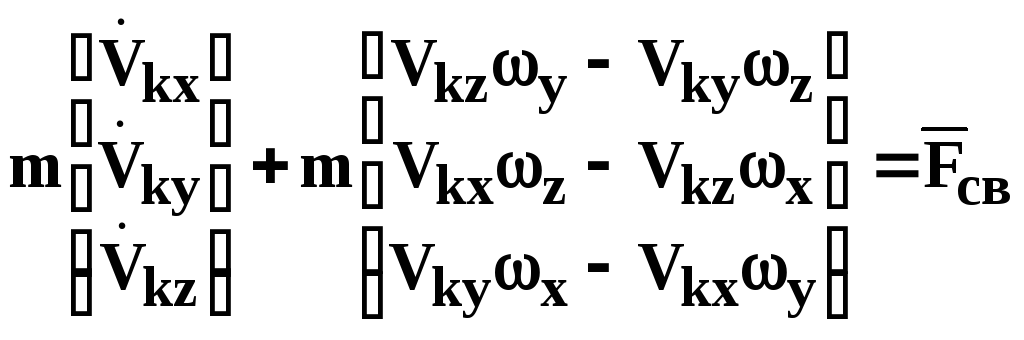
где
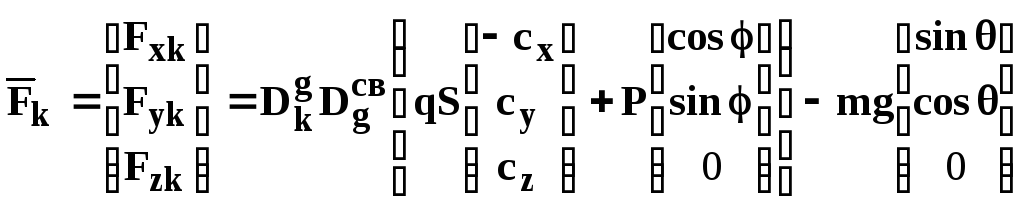 ,
,
 ,
,
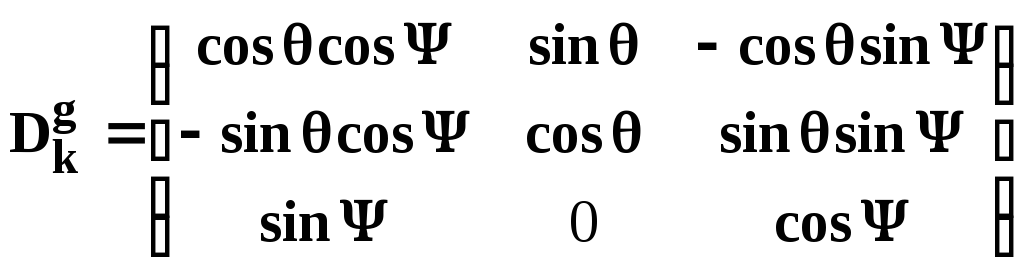 .
.
Кинематика углового движения:
|
для углов тангажа, рыскания, крена (уравнения Эйлера)
|
для матрицы направляющих косинусов (уравнения Пуассона)
где
|
Динамика углового движения:
 ,
,
где
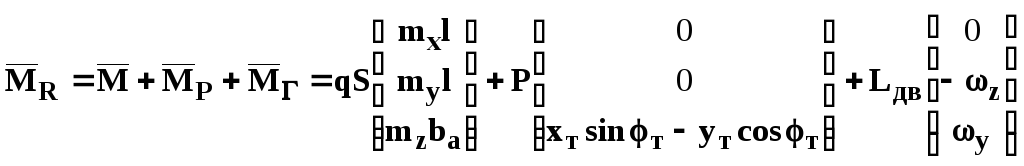 .
.
Воздушная скорость и углы атаки и скольжения, необходимые для вычисления аэродинамических сил и моментов:
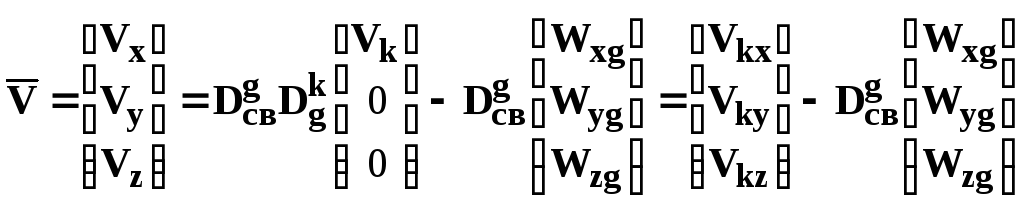 ,
,
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() .
.

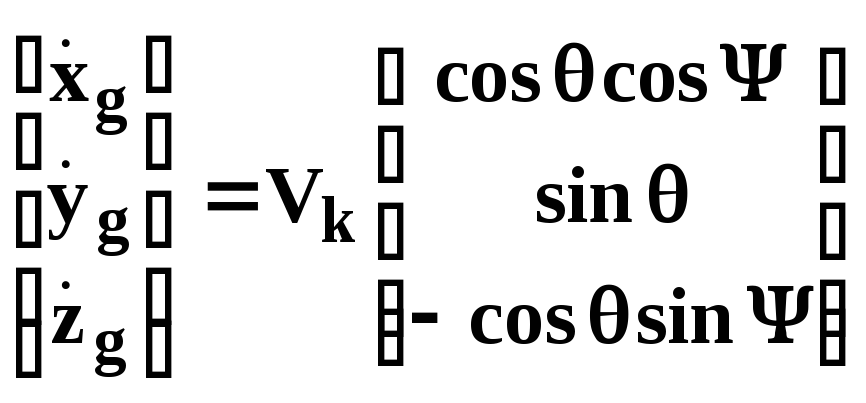 ,
,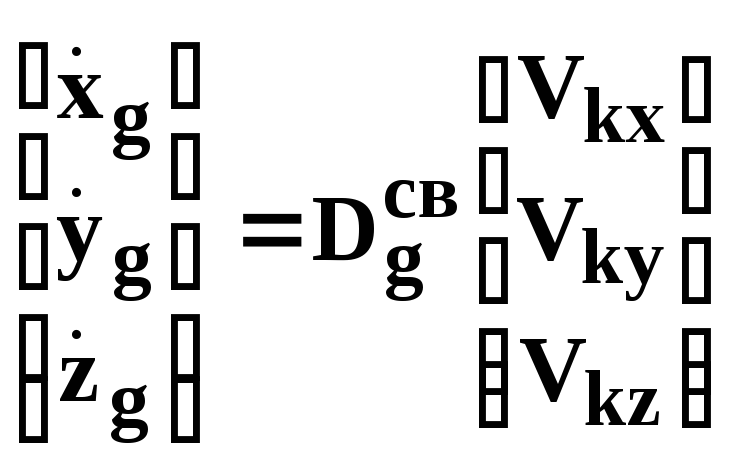 ,
,