Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Телекоммуникаций и Информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

647_Pinegina_T.JU._Praktikum_po_kursu_fiziki_

.pdf

Скачиваний:

Добавлен:

12.11.2022

Размер:

2.2 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

то уравнение тока в LC– контуре

I dq q

sin

5) Энергия колебаний:

механических –

Wпот

kx2

Wкин

Wполн

kA2

m 02 A2

;

электромагнитных – W

q 2

;

; W

q 2

L 2 q 2

эл

магн

полн

6) Период колебаний смещения, скорости, ускорения при механических коле-

баниях и заряда, напряжения на конденсаторе и тока в LC – контуре T 2 .

Период колебаний энергии

7) Затухающие механические колебания

Дифференциальное уравнение (механические колебания пружинный маят-

ник):

d 2 x 2 dx 2 x 0;

где

k ,

( r

– коэффициент тре-

dt 2

ния).

Уравнение затухающих колебаний

есть решение дифференциального урав-

нения: x Ae t

cos(

зат

t ) или x Ae t

sin(

зат

t ).

Частота затухающих колебаний:

зат

. Период затухающих коле-

баний:

зат

8) Затухающие электромагнитного колебания

Дифференциальное

уравнение

затухающих

колебаний

LCR– контуре:

d 2q

R dq

q 0 ,

коэффициент затухания

R .

dt2

L dt

Амплитуда затухающих колебаний заряда на конденсаторе изменяется по за-

кону:

e t .

Амплитуда напряжения на конденсаторе U

q0 e t

e t

Уравнения колебаний силы тока в LCR – контуре:

I q e t

cos(

t ), где

arctg

зат

Частота затухающих колебаний в LCR – контуре:

зат

Период затухающих электромагнитных

колебаний: T	2	2				2
колебаний: T
зат	зат	0	2 2				R 2
	зат	0	2 2	1			R 2


					LC		2L

9) Энергия колебаний в контуре складывается из энергии электрического поля и энергии магнитного поля:

CU 2

q02

e 2 t cos2

зат

LI 2

LI02

e 2 t

sin 2

зат

Полная энергия

LCR

– контура

любой

момент

времени t равна:

q02

e 2 t

LI02

e 2 t W e 2 t ,

где W0

– полная энергия контура в

полн

момент времени t = 0.

9) Характеристики затухающих колебаний Время релаксации.

Промежуток времени τ, за который амплитуда уменьшается в «е» раз), где «е» – основание натурального логарифма, е ≈ 2,718, называется временем затухания (или временем релаксации).

Коэффициент затухания – величина, обратно пропорциональная времени

релаксации 1

Логарифмический декремент затухания – физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период:

	A ( t )		A	зат	e t
ln	зат	ln				T .
	Aзат ( t T )		Aзат e ( t T )

Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) на отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:

Q 2	W( t )	2
		1 e2 .
	W( t ) W( t T )

При малых значениях логарифмического декремента δ добротность колеба-

тельной системы можно рассчитывать по формуле: Q		.

	T
		e

11) Вынужденные колебания

Дифференциальное уравнение вынужденных колебаний в механической си-

стеме

d 2 x

r dx

Учитывая обозначения

2 ,

0 cos t .

dt 2

m dt

, получим

d 2 x

cos t

0 f

Дифференциальное уравнение вынужденных колебаний в LCR – контуре с

генератором имеет вид:

m cos t

ЭДС генератора ме-

dt 2

няется с частотой по закону

cos t ,

R ,

1 .

Уравнение вынужденных колебаний:

q qm cos t 0

, где 0 – сдвиг фаз

между колебаниями ЭДС контура и заряда на пластинах конденсатора.

Амплитуда вынужденных колебаний

и сдвиг фаз зависят от частоты генера-

тора : qm

0 2 2 2 4 2 2

tg 0

2 2

12) Явление резкого возрастания амплитуды вынужденных колебаний при

приближении частоты вынуждающей силы к рез называется резонансом.

Частота,

при которой наступает резонанс, равна

рез.

2 2 (формула

верна и для механических вынужденных колебаний), величина резонансной

амплитуды заряда равна q рез

Резонанс

тока

колебательном

контуре

генератором

наступает

при

рез

. При этой частоте амплитуда тока в последовательном LCR

m .

– контуре максимальна и равна I

max

Для механических вынужденных колебаний амплитуда и частота вынужден-

ных колебаний при резонансе соответственно равны Aрез

;

2 2

рез.

2 2 2 .

13) Сложение двух колебаний одного направления (сложение сонаправлен-

ных колебаний)

x1 A1 cos( 1t 1 )

x2 A2 cos( 2t 2 )

с равными часто-

тами 1 2 .

Результирующее колебание xрез.

Aрез cos( t рез. ).

Амплитуда результирующего колебания A A 2

A 2

2A A cos(

) ,

начальная фаза

tg рез.

A1 sin 1

A2 sin 2

A1 cos 1

A2 cos 2

14) Сложение двух колебаний одного направления (сложение сонаправлен-

ных колебаний) x1 A1 cos( 1t 1 )		и	x2 A2 cos( 2t 2 ) с неравными, но
близкими частотами 1 2 ,	т.е.	разность		частот		2 1 1 ,
2 .
Если амплитуды складываемых колебаний одинаковы А1 А2							А, а началь-
ные фазы равны нулю 1 2	0 ,	то уравнения складываемых колебаний
примут вид: x1 A1 cos 1t , и x2	A2 cos 2t .
Результирующее колебание описывается уравнением:
		2 1 t				2 1 t
xрез. x1 x2 2Acos			2	cos		2	.
			2			2
Амплитуда результирующего колебания A				2A	cos t
Амплитуда результирующего колебания A				2A	cos t
			рез.			2
						2

Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями.

Время максимального изменения амплитуды результирующего колебания

называется периодом биений 2 б , период результирующего колебания

равен		2	4	T .

	1	2	1 2

		2

15) Складываются взаимно–перпендикулярные колебания с равными часто-
тами x y 0 :	x Ax cos 0t x , y Ay cos 0t y

Исключив время t из исходных уравнений для х и y, получим уравнение траектории на плоскости ОХУ, т.е. зависимость y f x :

x	2	y	2	xy	cos y x sin2 y x .
			2

				Ax Ay
Ax		Ay

В зависимости от разности начальных фаз колебаний ( y x ) траектория может быть прямой линией, эллипсом или окружностью ( Ax Ay )

Волны

1) Уравнение механической волны

Уравнение плоской бегущей упругой волны, которая распространяется вдоль оси ОУ в положительном направлении:

A cos( t 2 y ) A cos( t ky ).

Характеристики волны

k 2 – волновое число;

А – амплитуда; фаза волны

( t	2 y	) ( t ky)

2) Волновое уравнение, решением которого является уравнение плоской вол-

ны, имеет вид:	2	1	2	, где – фазовая скорость волны.
	y2	2	t 2

3) Если смещение любой точки среды с координатой y в момент времени t за-

		2 y
дано уравнением: Acos	t		, то скорость и ускорение этой точки

aточки

точки

A sin

x ,

cos

t 2

4) Фазовая скорость упругих волн в различных средах.

Твердое тело, поперечные волны: G , где G - модуль сдвига среды, –

плотность среды в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).

Твердое тело, продольные волны: E , Е – модуль Юнга.

Жидкости, продольные волны: K , где К – модуль объемной упругости

среды – величина, характеризующая способность среды сопротивляться изменению ее объема.

Идеальный газ продольные волны:

где – показатель адиабаты

газа, – его молярная масса, Т – абсолютная температура, R – универсальная

газовая постоянная.

Wполн.

5) Среднее значение плотности энергии волны:

Поток энергии, , волны

Wполн

2 A2 S

w S .

Вектор Умова: I

w .

Интенсивностью волны называется модуль среднего значения вектора Умова:

I w	2 A2
I w	2	.
	2
6) Разность фаз колебаний двух точек среды равна			2 y2 y1	k y .
6) Разность фаз колебаний двух точек среды равна				k y .

Величина y y2		y1 – разность расстояний между точками среды,		y1 , y2 –
расстояния точек от источника колебаний.

7) Разность фаз двух когерентных колебаний от когерентных источников в

данной точке пространства равна

2 y2 y1

k y , где y

y y

разность хода двух волн,

y1 , y2

– расстояния точки от когерентных источни-

ков колебаний.

8) Звуковые волны. Если

p0 , 0 – давление и плотность невозмущенной сре-

ды (среды,

по которой не проходит волна), а p, – давление и плотность

среды при

распространении

в ней

волнового процесса, то величина

p p0

называется избыточным

давлением.

Величина p0

pmax p0

есть максимальное значение избыточное давление (амплитуда избыточного давления).

Уравнение плоской звуковой волны имеет вид:

		y	2 y
p pm cos	t	) pm cos( t		),
p pm cos	t	) pm cos( t		),

где y – расстояние от источника колебаний точки, избыточное давление в ко-
торой мы определяем в момент времени t.
9) Электромагнитные волны.

Волновое уравнение плоской волны	2 E				2 E
Волновое уравнение плоской волны	y 2	0	0		t 2
	y 2	0	0		t 2
	2 H	0	0	2 H
	y2	0	0		t 2

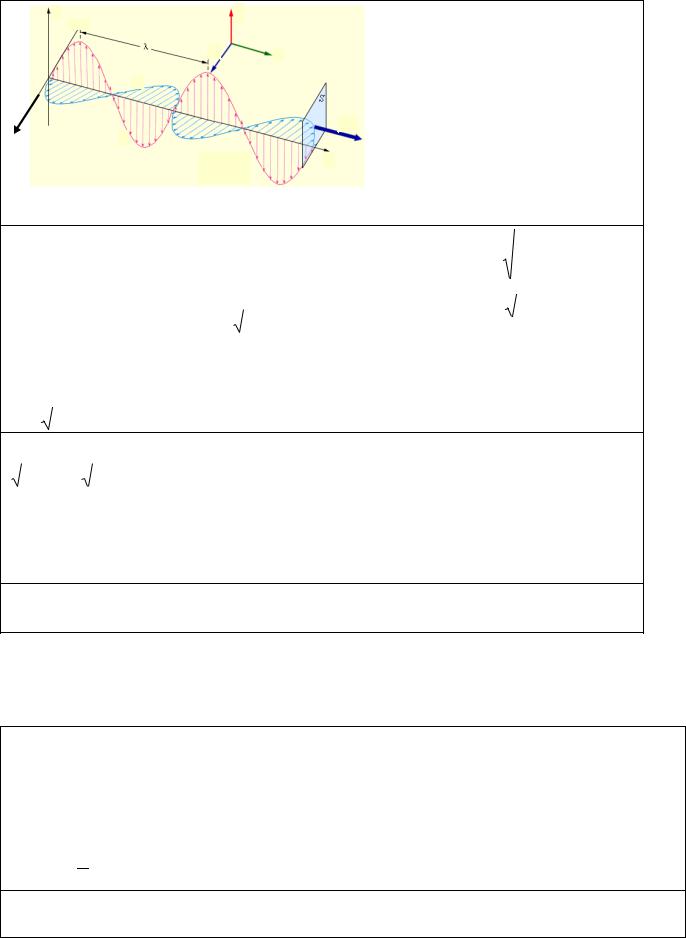
Решением дифференциального уравнения является уравнение волны. Уравнение плоской линейно поляризованной волны имеет вид:

Еz Еm cos t ky , H x H m cos t ky

где y – расстояние точки от источника колебаний.

	Z
Е

Рисунок П.3.1 График плоской электромагнитной волны

10) Уравнение фазовой скорости электромагнитных волн

. Ско-

рость света в вакууме c

3 108

, а величина n

показатель

0 0

преломления среды, в которой распространяется электромагнитная волна.

Фазовая скорость электромагнитной волны в диэлектрике равна

11) Для любого момента времени вектора E,

H связаны соотношением

0 Е

0 H , которое отражает синфазность колебаний векторов

и Н

в электромагнитной волне.

12) Объёмная плотность энергии электромагнитного поля равна

E 2

H 2

, направ-

13) Плотность потока энергии – вектор Пойнтинга – Р w E H

ление совпадает с направлением скорости волны.

4. МОЛЕКУЛЯРНАЯ И СТАТИСТИЧЕСКАЯ ФИЗИКА

Термодинамика

1) Если в газе содержится N частиц, то средняя кинетическая энергия их движения называется внутренней энергией:

U N W

k T

R T , где N

k R , - число молей га-

кин

N A

за, i - число степеней свободы молекулы газа. Изменение внутренней энергии рав-

но dU 2i R dT .

2) Работа газа равна A p S dх p dV , где p – давление газа, dV - изменение объёма.

3) Первое начало термодинамики (закон сохранения энергии в молекулярной физике) в дифференциальной форме имеет вид:

Q dU Aгазанад внешними силами .

		Совершенная
Тепло,		Совершенная
Тепло,	Приращение	системой	ра-
переданное	Приращение	системой	ра-
переданное	внутренней	бота	над
термодинамической	внутренней	бота	над
термодинамической	энергии систе-	внешними	си-
системе	энергии систе-	внешними	си-
системе	мы	лами
	мы	лами

Если использовать, что Aгаза над внешними силами Aвнешних сил над газом ,

то первое начало можно переписать в другом виде:

dU Q Aгаза над внешними силами

Q Aвнешних сил над газом

Совершенная

Изменение

Подводимое

внешними

внутренней

к системе

силами

энергии

тепло

работа над

системы

системой

Окончательно первое начало термодинамики Q

R dT pdV .

4) Удельная теплоемкость измеряется количеством теплоты, необходимой для нагревания одного килограмма вещества на один градус (обозначение суд , раз-

мерность с		Дж	):	с		Q
мерность с	уд		):	с	уд	m T
	уд	кг К			уд
		кг К

Молярная теплоемкость измеряется количеством теплоты, необходимой для нагревания одного моля вещества на один градус (обозначение Смол , размерность)

Смол суд , где – молярная масса вещества, размерность молярной теплоём-

кости Смол

Дж

моль К

5) Молярная теплоёмкость при постоянном объёме равна

молV

Молярная теплоемкость при постоянном давлении равна

мол p

i 2

Уравнение Майера для молярных теплоёмкостей Смол p СмолV

R ,

а для удельных

теплоемкостей cуд p cудV

Отношение теплоемкости при постоянном давлении к теплоёмкости при постоянном объёме называется коэффициентом Пуассона (или показателем адиабаты):

С р

i 2

СV

6) Первое начало термодинамики для изопроцессов:

Название

про-

Уравнение про-

Количество тепло-

Работа в процессе

Изменение

цесса

ты,

сообщаемое

внутренней

процессе

энергии

процессе

Изохорический

V const

Q CV T

A 0

U CV T

const

Изобарический

V const

Q C p T

A p V

U CV T

const

Изотермический

T const

Q A

R T ln

U 0

pV const

R T ln

Адиабатический

pV const ;

Q 0

A p dV U

U A CV T

Q 0

CV T

pT 1

const ;

p1V1

p2V2

VT 1

const

Политропный

pV n const ;

Q CV

U CV T

теплоёмкость

n 1

С const

const ;

pT 1 n

показатель

по-

литропы

n 1

const

n 1

C Cp

C C

7) Изменение энтропии выражается общей формулой S S

. При бес-

конечно малом изменении температуры dT нагреваемого тела,

затрачивается

ко-

личество теплоты dQ mc dT , где

m - масса тела, с – удельная теплоёмкость.

Величина Q называется приведенным количеством тепла. Это соотношение вер-

но для любого квазистационарного процесса. Оно называется основным термодинамическим соотношением. Функция состояния, дифференциалом которой являет-

ся приведенная теплота Q , называется энтропией

8) Изменение энтропии при изотермическом процессе S	1	RT ln	V2	Q	, где Q

	T	V1		T

– тепло, которое надо подвести к системе, чтобы обратимо перевести систему из

начального состояния в конечное.

При адиабатическом процессе S const ; S 0 .

При любом обратимом круговом процессе приведенное тепло, сообщенное телу

равно нулю, поскольку Q S 0 .

10) Процесс, в котором теплоёмкость остается неизменной, называется политропным.

Показатель политропы	n	C Cp

		C C
		V

При С = 0, n = γ, получается уравнение адиабаты; при С = 0, n = 1 — уравнение изотермы; при С = Сp, n = 0 —уравнение изобары, при С = СV, n = ±∞ — уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.

Изменение энтропии при политропном процессе S	R n		T2
			ln
	1	n 1		T
			1

11) Коэффициентом полезного действия теплой машины (теплового двигателя) называется отношение работы, совершённой рабочим телом за цикл Aза_цикл, к количеству теплоты, которое рабочее тело получило за цикл от нагревателя, Q1:

Аза _ цикл	Q Q	1	Q	идеал	T T	1	T	,
	1 2		2		1 2		2
Q1	Q1		Q1		T1		T1
Q1	Q1		Q1		T1		T1

где Q1 – количество тепла, полученное от нагревателя за цикл, Q2 - количество

тепла, отданное холодильнику за цикл. Этот КПД будет всегда меньше или равен КПД идеальной тепловой машины, работающей по циклу Карно, у которой тепло передается рабочему телу при постоянной температуре T1, а передается холодиль-

нику при постоянной температуре T2 . Формулу с температурами можно использо-

вать в качестве завышенной верхней оценки КПД произвольного цикла, если под T1 и T2 понимать максимальную и минимальную температуры рабочего тела в цикле.

12) Термодинамические потенциалы


	dU T dS p dV	U внутренняя энергия системы

	dH d U pV T dS V dp	H энтальпия системы
	dF d U T S S dT p dV	F свободная энергия системы
	dФ d H T S S dT Vdp	Ф термодинамический потенциал
		Гиббса

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20225.17 Mб13637_Nosov_V.I._Seti_radiodostupa_CH.2_.pdf
#
12.11.20223.71 Mб10638_Nosov_V.I._RRL_STSI_Osnovy_TSPS__i_postroenija_RRL_.pdf
#
12.11.20222.45 Mб2639_Nosov_V.I._RRL_STSI._Mnogourovnevyj_kodek_.pdf
#
12.11.2022525.57 Кб2644_Galkina_M.JU._Vychislitel'naja_matematika_.pdf
#
12.11.20221.76 Mб4645_Galkina_M.JU._Metody_optimal'nykh_reshenij_.pdf
#
12.11.20222.2 Mб15647_Pinegina_T.JU._Praktikum_po_kursu_fiziki_.pdf
#
12.11.2022736.72 Кб2651_Zelentsov_B.P._Matrichnye_modeli_funktsionirovanija_.pdf
#
12.11.20229.18 Mб5652_Maglitskij_B.N._Printsipy_postroenija_sputnikovogo_televidenija_.pdf
#
12.11.2022811.62 Кб3656_Lytkina_D.V._Algebraicheskie_struktury_.pdf
#
12.11.20225.99 Mб5657_Smolovik_G.N._Teorija_menedzhmenta_.pdf
#
12.11.20221.69 Mб15658_Markasov_M.JU._Teorija_i_praktika_massovoj_informatsii_.pdf