651_Zelentsov_B.P._Matrichnye_modeli_funktsionirovanija_

Перейдем теперь к укрупнению состояний. Матрицы вероятностей возвращения AU и AV состоят из одинаковых строк. В каждой из них имеется нулевой столбец. Удалив его и соответствующую строку, получим:

AU = ( 1 ); AV = ( 1 ); rU = ( 1 ); rV = ( 1 ),

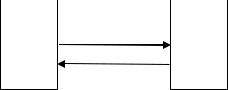
Таким образом, каждое из подмножествах U и V можно заменить одним состоянием, обозначенных u и v на рис. 8.2, то есть данную систему из четырех состояний можно представить системой из двух состояний. При этом сохраня-

ются средние времена нахождения в состояниях (tu = 2550 час ; tv = 1,01 час), коэффициент простоя и частота отказов системы.

1

u v

1

Рис. 8.2. Укрупненная система из двух состояний

8.2. МОДЕЛЬ ФУНКЦИНИРОВАНИЯ ДУБЛИРОВАННОЙ СИСТЕМЫ

Рассматривается дублированная система, которая состоит из двух элементов

(устройств), обозначаемых Э1 и Э2. Элемент Э1 будем считать основным, а

элемент Э2 – резервным. Элементы полностью дублируют выполняемые функции. Система работоспособна, если работоспособен хотя бы один элемент, и система отказывает, если отказывают оба элемента. Если отказывает основной элемент, то его функции выполняет работоспособный резервный элемент. Отказы основного и резервного элементов обнаруживаются при их возникновении. Система является восстанавливаемой, то есть после отказа оба элемента восстанавливаются. Выберем вариант такой системы в соответствии со следующими особенностями.

81

Особенности, связанные с безотказностью и функционированием элементов:

1)если оба элемента работоспособны, то функционирует основной элемент,

арезервный находится в ненагруженном (холодном) режиме; в этом состоянии отказать может только основной элемент, а резервный отказать не может;

2)если работоспособен только один элемент, то он и выполняет функции (функционирует), при этом он может отказать.

Особенности, связанные с восстановлением:

1)имеется один восстанавливающий орган (случай ограниченного восстановления), что означает: одновременно может восстанавливаться только один элемент;

2)восстановление основного элемента начинается одновременно с его отка-

зом;

3)приоритет в восстановлении имеет основной элемент, то есть при отказе двух элементов сначала восстанавливается основной элемент, а затем – резервный.

Для упрощения задачи будем полагать, что основной и резервный элементы имеют одинаковые характеристики безотказности и ремонтопригодности: интенсивность отказов обозначена через λ, а интенсивность восстановления – через μ.

Для обозначения состояний (фаз) эксплуатации элементов используется следующая символика: Ф – функционирование работоспособного элемента; Н – неработоспособное состояние элемента; Х – холодный (ненагруженный) режим резервного элемента; В – восстановление элемента. На графе состояний индекс при этих состояниях указывает элемент: для основного элемента используется индекс 1, а для резервного – индекс 2.

Состояния дублированной системы обозначены такой комбинацией букв и индексов, чтобы эта комбинация полностью характеризовала состояние систе-

мы. Возможны следующие состояния системы: Ф1Х2 – основной элемент функ-

ционирует, а резервный находится в холодном (ненагруженном) режиме; В1Ф2

– резервный элемент функционирует, а основной восстанавливается; Ф1В2 –

основной элемент функционирует, а резервный восстанавливается; В1Н2 – основной элемент восстанавливается, а резервный находится в неработоспособном состоянии (ожидает начало восстановления). Переходы от состояния к состоянию показаны на рис. 8.3.

Рис. 8.3. Граф состояний дублированной системы

82

В состоянии 1 может отказать только основной элемент (переход в состояние 2). В состоянии 2 функционирует резервный элемент, а основной элемент восстанавливается. Функционирующий резервный элемент может отказать с интенсивностью λ, что вызывает переход в состояние 4, в котором продолжается восстановление основного элемента, а неработоспособный резервный элемент «стоит в очереди на восстановление». После завершения восстановления основного элемента происходит переход в состояние 3, где восстановление пе-

реключается на резервный элемент (В2), а функционирующий основной может опять отказать с интенсивностью λ, что вызывает переход в состояние 4, в котором в соответствии с приоритетом сначала восстанавливается основной элемент, а резервный, находясь в неработоспособном состоянии, «стоит в очереди на восстановление». Очевидно, что в состояниях 1, 2, 3 система работоспособна, а в состоянии 4 – неработоспособна.

Следует отметить, что рассмотренный здесь пример является простым, иллюстративным. В реальных дублированных системах элементы системы имеют разные интенсивности отказов и восстановления, что обусловлено их разной конструкцией, они могут быть продуктом разных фирм, произведены в разное время, имеют разную технологию и трудоемкость устранения отказов. Кроме того, могут быть более сложные связи между элементами и их состояниями, например, элементы системы могут быть охвачены контролем технического состояния и профилактическим обслуживанием.

Найдем предельные вероятности состояний по формуле (2.13) и на их основе вычислим коэффициенты готовности и простоя системы. Для этого составим матрицу интенсивностей:

Соответствующие определители, полученные из матрицы Λ:

Теперь получаем формулы для вычисления предельных вероятностей состоя-

ний:

π1 = – μ2/( λ2 + λμ + μ2); π2 = – λμ2/ Δ; π3 = – λ2μ / Δ; π4 = – λ2/( λ2 + λμ + μ2).

83

Коэффициенты готовности и простоя системы:

Кг = π1 + π2 + π3 = (λ + μ)·μ /( λ2 + λμ + μ2); Кп = π4 = λ2/( λ2 + λμ + μ2).

Для значений λ = 0,01 1/час и μ = 1 1/час получаем следующие значения предельных вероятностей состояний:

π1 = 0,9900; π2 = 0,0098; π3 = 0,0001; π4 = 0,0001.

Значения коэффициентов готовности и простоя: Кг = 0,9999; Кп = 0,0001. Для сравнения найдем коэффициенты готовности и простоя одного восстанавливаемого устройства (рис. 8.4), коэффициенты готовности и простоя кото-

μ

Рис. 8.4. Граф состояний одного восстанавливаемого устройства

Для значений λ = 0,01 1/час и μ = 1 1/час получаем Кг= 0,99; Кп = 0,01. Эффект от использования дублирования выразим в виде отношения коэф-

фициентов простоя:

Eff = Кп/Кп = (α + α2)/(1+ α + α2),

где α = λ/μ – отношение интенсивностей отказов и восстановления.

Для приведенных значений λ и μ получаем Eff = 0,01, то есть коэффициент простоя дублированной системы уменьшается в 100 раз по сравнению с коэффициентом простоя одного элемента с такими же исходными параметрами.

Разобьем множество состояний на два подмножества по признаку безотказности: подмножество работоспособных состояний U = {1, 2, 3} и подмножество неработоспособных состояний V = {4}. Соответствующие подматрицы интен-

Выведем формулы для вычисления математического ожидания и дисперсии времени нахождения в подмножестве работоспособных состояний. Для любых начальных условий следует находить матрицу TU путем обращения матрицыUU. Матрица TU имеет вид:

84

Замечание. Матрицу TU можно получить вручную несколькими методами или с помощью таких инструментов, как Mathcad или Mathlab.

В табл. 8.2. приведены формулы для математического ожидания и дисперсии времени нахождения в подмножестве U при трех начальных условиях:

1)состояние 1 является начальным, rU = r1;

2)состояние 2 является начальным, rU = r2;

3)состояние 3 является начальным, rU = r3.

Табл. 8.2. Формулы для вычисления математического ожидания tU и дисперсии DU времени нахождения в подмножестве U при разных начальных условиях

Видно, что значения характеристик подмножества U зависят от начального состояния. Однако насколько существенна эта зависимость, определяется также значениями исходных параметров (в данном случае λ и μ). В табл. 8.3 приведены значения математического ожидания tU и среднего квадратического отклонения σU для двух вариантов значений параметров λ и μ (значения приведены в часах).

Табл. 8.3. Значения математического ожидания tU и среднего квадратического отклонения σU времени нахождения в подмножестве U при разных начальных условиях λ μ

85

В данной системе при заданных значениях интенсивности отказов и интенсивности восстановления среднее время безотказной работы tU и среднее квадратическое отклонение этого времени σU практически не зависят от начального состояния. Кроме того, среднее время безотказной работы и среднее квадратическое отклонение этого времени практически совпадают. Это свидетельствует о том, что время безотказной работы рассматриваемой дублированной системы можно считать распределенным по показательному закону при любом начальном состоянии.

Рассмотрим циклическое функционирование системы. Матрицы вероятностей попаданий и матрицы вероятностей возвращения:

1

BUV = – UU1 UV = 1 ; BVU = – VV1 VU = 0 0 1 ;

1

Предельные распределения вероятностей возвращения имеют вид:

Средние времена нахождения в подмножествах состояний: tU = –rU · UU1 ·e = (λ+μ)/λ2; tV = –rV · VV1 ·e = 1/μ.

В рассматриваемой модели tU имеет смысл среднего времени безотказной работы, а tV – среднего времени восстановления. Среднее время цикла:

tUV = tU + tV = (λ2+λμ+μ2)/λ2μ.

Отсюда коэффициенты готовности и простоя системы:

Кг = tU /tUV = (λ + μ)μ / ( λ2 + λμ + μ2) ; Кп = tV /tUV = λ2 / ( λ2 + λμ + μ2),

что согласуется с ранее полученным результатом.

Эти показатели в числах при λ = 0,01 1/час и μ = 1 1/час: tU = 10 000 час, tV =

1 час, tUV = 10 001 час, Кп = tV /tUV = 0,0001.

Исследуем систему с помощью частотного метода. Подматрицы частот переходов:

= 1/tUV, что согласуется с ранее полученным результатом.

Рассмотрим теперь возможность укрупнения состояний. Усеченные матри-

Усеченные матрицы средних времен нахождения в состояниях:

8.3.МОДЕЛЬ ФУНКЦИНИРОВАНИЯ ОБОРУДОВАНИЯ В УСЛОВИЯХ КОНТОЛЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ

Устройство функционирует в условиях недостоверного контроля. Отказы устройства обнаруживаются только при проверках в рамках периодического контроля, который является недостоверным. Имеются ошибки контроля I рода с вероятностью α и ошибки контроля II рода с вероятностью β. Во время проверки устройство отказать не может.

Полагается, что все события происходят в случайные моменты времени, а время до наступления этих событий распределено по показательному закону с соответствующей интенсивностью. Соответственно время нахождения процесса в каждом состоянии является случайным и распределено по показательному закону.

Принято, что периодические проверки проводятся в случайные моменты времени. Одним из факторов, обуславливающих случайность периодических проверок, является следующий: зачастую периодические проверки проводятся в то время, когда оборудование простаивает (не нагружено), а эти моменты времени случайны. Алгоритм проверок может также вносить элементы случайности в продолжительность проверок.

Граф состояний приведен на рис. 8.5. Для удобства составления модели состояния пронумерованы и снабжены буквенными обозначениями. Строки и столбцы используемых матриц интенсивностей расположены в порядке номеров состояний.

Рассматривается вариант модели с пятью состояниями: ФР – функционирование работоспособного устройства;

ФН – функционированиенеработоспособногоустройства(имеетсяскрытыйотказ); ПР – периодическая проверка работоспособного устройства; ПН – периодическая проверка неработоспособного устройства; В – восстановление устройства.

Использованы следующие обозначения: λ – интенсивность отказов;

γ – интенсивность начала периодической проверки;

μп – интенсивность завершения периодической проверки; μв – интенсивность завершения восстановления;

α – вероятность ошибки контроля I рода;

β - вероятность ошибки контроля II рода.

87

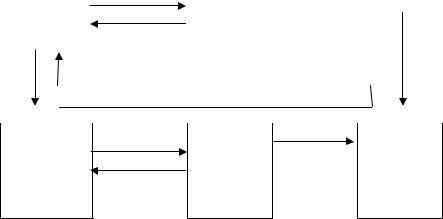
В случайный момент времени происходит отказ устройства с интенсивностью λ (переход 1→2). С интенсивностью γ производится проверка устройства с экспоненциальным распределением ее начала. В результате ошибки контроля первого рода

работоспособное устройство с интенсивностью αμп поступает на восстановление

(переход 3→5) и с интенсивностью (1– α)μп продолжает функционировать. Если проверяется неработоспособное устройство, то в результате ошибки контроля второ-

го рода неработоспособное устройство с интенсивностью βμп возвращается на функционирование (переход 4→2) и с интенсивностью (1–β)μп поступает на восстановление. После восстановления имеет место переход в работоспособное состояние

1 с интенсивностью μв.

βμп

Рис 8.5. Граф состояний эксплуатации устройства

Матрица интенсивностей имеет вид:

Проверка правильности составления матрицы интенсивностей: |Λ| = 0. Вычисления предельных вероятностей состояний в символьном виде с по-

мощью определителей или путем обращения матриц приводит к сложным формулам. Вычисления упрощаются при составлении модели на основе полумарковского процесса.

88

По матрице интенсивностей найдем матрицу вероятностей прохождений:

Перейдем к циклическому функционированию с применением укрупнения состояний. Множество состояний системы разобьем на подмножества U и V по признаку фаз эксплуатации: U = {1, 2, 3, 4} и V = {5}. Разбиение матрицы P на подматрицы:

Матрицы вероятностей попаданий и матрицы вероятностей возвращения:

Матрица средних времен нахождения в состояниях подмножества U при однократном попадании в них:

Строка средних времен нахождения в состояниях подмножества U до выхода из этого подмножества:

Для упрощения последующих выкладок будем считать, что среднее время периодической проверки намного меньше среднего времени до отказа и среднего

времени между проверками, то есть μп >> λ, μп >> γ. В модели это выражается в том, что принимается μп = ∞. Тогда строка средних времен нахождения в состояниях примет вид:

В подмножество U входят состояния, различные по своему функциональному назначению. Так, состояния 1 и 2 характеризуются временем нахождения в них, а состояния 3 и 4 – числом вхождений в эти состояния. Поэтому подмно-

жество U целесообразно описывать векторами nU и tU . Укрупненную систему можно представить двумя состояниями u и v (рис. 8.2) с переходными вероятностями 1 между входными состояниями. Состояние u следует характеризовать

векторами nU и tU .

Приведенные матричные характеристики могут быть использованы для получения обобщенных (выходных) характеристик функционирования устройства. В табл. 8.4 приведен ряд таких характеристик устройства, которые могут быть полезны при исследовании эксплуатации устройства.

На основе приведенной модели может быть исследовано влияние недостоверности контроля на эксплуатационные характеристики устройства. В частности, ошибки контроля I рода не влияют на значения коэффициентов готовности и простоя. В рассматриваемом варианте они влияют на среднее время цикла и коэффициент использования. Однако коэффициенты готовности и простоя существенно зависят от ошибок контроля II рода: при увеличении вероятности ошибки контроля II рода уменьшается коэффициент готовности и увеличивается коэффициент простоя.

90