651_Zelentsov_B.P._Matrichnye_modeli_funktsionirovanija_

Пусть процесс начинается также в состоянии wi, то есть начальная вероят-

ность qii (0) = 1. Выпишем очевидные соотношения:

qii (0) = 1; qii (1) = qii (0) pii = pii; qii (2) = qii (1) pii = pii2; qii (3) = qii (2) pii = pii3; … qii (n) = qii (n – 1) pii = piin.

Среднее число шагов нахождения в состоянии wi до выхода из него определяется суммой этих вероятностей, которая представляет собой сходящийся геометрический ряд (геометрическую прогрессию):

Таким образом, среднее число шагов нахождения в состоянии wi до выхода из него будет θii(n) = 1/(1– pii).

Из этой формулы следует: чем больше вероятность pii, тем больше среднее время нахождения в состоянии wi. Эта зависимость иллюстрируется табл. 1.1.

Табл. 1.1. Зависимость среднего числа шагов нахождения в состоянии wi от ве-

роятности pii.

1.5. КЛАССИФИКАЦИЯ СОСТОЯНИЙ

Рассмотрим следующие типы (классы) состояний: достижимые, сообщающиеся, несущественные и существенные, эргодическое множество и поглощающие состояния.

Состояние wj достижимо из состояния wi, если за некоторое число шагов система переходит из wi в wj, то есть существует такое n, что pij(n) > 0, где pij(n)– вероятность того, что S(n) = wj при условии, что начальным является состояние wi: pij (n) = p[S(n) = wj / S(0) = wi]. Состояние wj не достижимо из состояния wi, если не существует такого числа шагов n, при котором pij (n) > 0.

Смысл достижимости: если из wi можно по стрелкам пройти в wj, то со-

стояние wj достижимо из wi.

На рис 1.4 состояние w4 достижимо из состояния w1, однако w1 не достижимо из w4.

11

w1 w2 w3 w4

Рис.1.4. Пример достижимых и не достижимых состояний

Замечание. Здесь и далее на рисунках не указаны вероятности pii. Отсутствие этих вероятностей на рисунках не меняет смысла приведенных иллюстраций.

Сообщающимися называются состояния wi и wj, если они взаимно достижи-

мы, то есть существуют такие m и n, что pij (m) > 0, pji (n) > 0.

Пример. На рис 1.5 все состояния взаимно достижимы, в том числе состоя-

ния w1 и w2, то есть все состояния сообщаются.

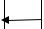w1 w2 w3 w4

Рис.1.5. Пример взаимно достижимых состояний

Состояние wi называется несущественным, если имеется такое состояние wj и такое число шагов m, что pij (m) > 0, однако pji (n) = 0 при любом n. Состояние wi называется существенным, если не имеется таких состояний wj, то есть любое состояние, достижимое из wi, сообщается с этим состоянием wi.

Смысл этих состояний. Для несущественного состояния wi имеется дости-

жимое из него состояние wj, однако wi не достижимо из wj. Иными словами, из каждого несущественного состояния система каким-либо образом может уйти в одно из существенных состояний и больше никогда в это несущественное состояние не вернется.

Несущественные и существенные состояния образуют соответственно множества несущественных и существенных состояний. Попав в множество существенных состояний, система никогда из него не выйдет.

На рис.1.6. состояния w1 и w2 являются несущественными, а состояния w3, w4, w5 образуют множество существенных состояний.

несущественные состояния w1 w2

w3 w4 w5

существенные состояния

Рис.1.6. Пример существенных и несущественных состояний

12

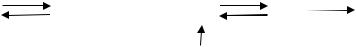
Теорема. При n конечная цепь Маркова будет находиться только в существенных состояниях.

Теорема приведена без доказательства.

Смысл теоремы: если начальным является несущественное состояние, то с течением времени вероятность нахождения в несущественных состояниях стремится к нулю, то есть при n конечная цепь Маркова будет находиться только в существенных состояниях.

Эргодическое множество состояний – это множество существенных сообщающихся состояний.

Смысл эргодического множества: из любого состояния можно попасть в любое другое состояние и из этого множества нельзя выйти (после попадания в него), то есть система, попадающая в эргодическое множество, никогда его не покидает.

На рис.1.7 приведены два процесса состояние с эргодическим множеством состояний.

Рис.1.7. Два примера эргодического множества состояний

Поглощающим называется состояние, если система после попадания в это состояние из него не выходит. Если wi – поглощающее состояние, то переход-

ные вероятности pii = 1 и pij = 0 для всех j i.

Цепь Маркова с поглощением – это цепь, множество состояний которой содержит хотя бы одно поглощающее состояние.

Замечание. Поглощающее состояние можно рассматривать как частный случай эргодического множества, состоящего из одного состояния.

1.6. МАТРИЦА ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ

Матрица переходных вероятностей является матричной характеристикой пе-

реходов между состояниями однородной марковской цепи: P = pij . Матрица переходных вероятностей является стохастической. Это значит, что

она обладает двумя свойствами:

1)свойством неотрицательности, pij 0;

2)свойством нормированности: сумма элементов любой строки равна 1 или P·e = e, где – столбец, все элементы которого равны 1.

Каждая i-я строка представляет собой распределение условных вероятно-

стей перехода pi1, pi2, pi3, …

Если множество состояний является конечным, то матрица переходных вероятностей является квадратной.

Замечание. После составления матрицы переходных вероятностей целесообразно сделать проверку условия |E – P| = 0, где E – единичная матрица.

13

1.7. ВЕРОЯТНОСТИ СОСТОЯНИЙ ОДНОРОДНОЙ ЦЕПИ МАРКОВА

Вероятностью состояния на произвольном шаге называется вероятность то-

го, что на n-м шаге система будет в состоянии wj при условии, что состояние wi

было начальным: pij (n) = p[S(n) = wj / S(0) = wi], где S(0) состояние системы на начальном шаге.

Выведем рекуррентную формулу для вычисления этих вероятностей.

Пусть состояние wi является начальным. На (n 1)-м шаге система будет на-

ходиться в состоянии wk с вероятностью pik(n 1), из которого на n-м шаге она попадает в состояние wj. Поэтому вероятность попадания в состояние wj через состояние wk равна pik(n 1) pkj. По формуле полной вероятности вероятность попадания в состояние wj на n-м шаге

Замечание. Суммирование ведется по всему множеству состояний.

Для нахождения вероятностей состояний и других характеристик системы в переходном и стационарном режимах целесообразно пользоваться методами матричного исчисления. Будем записывать вероятности состояний цепи Марко-

ва pij(n) в виде матрицы: P(n) = pij(n) .

Формула (1.2) для вероятности pij(n) в матричном виде запишется следующим образом:

Каждый элемент матрицы P(n) представляет собой произведение i-й строки матрицы P(n 1) на j-й столбец матрицы P.

Замечания. 1. Получено прямое уравнение А.Н.Колмогорова для марковской цепи в отличие от обратного уравнения: P(n) = P P(n 1).

2. Уравнение А.Н.Колмогорова в более общем виде:

а) в развернутой форме: pij (m + n) = pik (m) pkj(n); k

б) в матричной форме: P(m + n) = P(m) P(n).

Для однородной марковской цепи матрицы вероятностей состояний на первом, втором и т.д. шагах имеют вид: P(1) = P(0) P = E P = P; P(2) = P(1) P = P2;

P(3) = P(2) P = P3; P(4) = P(3) P = P4; … P(n) = P(n 1) P = Pn,

где P(0) = E единичная матрица.

Замечания. 1. Принято, что P(0) = P0 = E является единичной матрицей. 2. Матрица P(n) является стохастической.

На начальном шаге (n = 0) начальным может быть не одно, а несколько состояний. В этом случае задают начальные вероятности состояний.

14

Начальная вероятность pi(0) состояния wi это вероятность того, что в нача-

ле процесса, то есть на начальном шаге, система находится в состоянии wi: pi(0) = p[S(0) = wi]. Будем записывать начальные вероятности в виде распреде-

ления (строки): p(0) = p1(0) p2(0) p3(0) … pm(0) .

Распределение начальных вероятностей состояний является стохастическим, то есть оно обладает свойствами неотрицательности и нормированности:

pi(0) 0; p(0) e= pi(0) 1 i

для всех i, где e– столбец, все элементы которого равны 1.

Если начальным является одно определенное состояние wi, то элемент, со-

ответствующий этому состоянию, равен 1, то есть pi(0) =1, а остальные элементы равны нулю. Например, если начальным является первое состояние, то

p(0) = 1 0 0 0 … 0 .

Распределение вероятностей состояний на n-м шаге будем записывать в виде сроки: p(n) = p1(n) p2(n) p3(n) … pm(n) . Очевидно, что j-й элемент этой строки равен произведению строки p(n 1) на j-й столбец матрицы P, или

Запишем эту рекуррентную формулу для n = 1, 2, 3, 4, … и для общего слу-

чая: p(1) = p(0) P ; p(2) = p(1) P = p(0) P2 ; p(3) = p(2) P = p(0) P3 ; p(4) = p(3) P = p0) P4 ; … p(n) = p(n 1) P = p(0) Pn .

Замечание. Строка p(n) является стохастической.

Итак, получены распределения вероятностей состояний цепи Маркова на произвольном шаге при фиксированном начальном состоянии и при заданном начальном распределении. Формулы для вычисления этих распределений приведены в табл. 1.2.

Табл. 1.2. Формулы для вычисления вероятностей состояний при разных начальных условиях

15

1.8. ПРЕДЕЛЬНЫЕ ВЕРОЯТНОСТИ ЭРГОДИЧЕСКОЙ ЦЕПИ МАРКОВА

Эргодическая цепь Маркова – это такая цепь, множество состояний которой образует одно эргодическое множество.

Предельной вероятностью j состояния wj эргодической цепи Маркова называется вероятность нахождения в этом состоянии при n , то есть в далеком будущем.

Синонимы: финальная вероятность, стационарная вероятность.

Смысл предельной вероятности: j есть средняя доля числа шагов нахожде-

ния в состоянии wj при бесконечном протекании процесса.

Теорема о существовании и единственности предельных вероятностей.

Для эргодической однородной цепи Маркова существует единственное предельное распределение вероятностей состояний, не зависящее от начального состояния:

Теорема приведена без доказательства.

Смысл теоремы: предельные вероятности j существуют и не зависят от того, каким было начальное состояние.

Замечания. 1. Другая возможная формулировка приведенной теоремы: Для того чтобы существовали предельные вероятности, не зависящие от начального состояния, необходимо и достаточно, чтобы цепь была эргодической.

2. Иногда эргодическую цепь определяют через существование предельных вероятностей: цепь Маркова называется эргодической, если для нее существуют предельные вероятности, не зависящие от начального состояния.

Поскольку вероятности j не зависят от начального состояния, то они не зависят и от начального распределения, то есть lim p(n) π,

Следующая теорема связывает распределение π и матрицу P.

Теорема о связи предельных и переходных вероятностей эргодической цепи.

Замечание. Распределение π называют также финальным, стационарным, предельным, инвариантным; иногда его называют еще неподвижным вектором матрицы P.

Смысл теоремы. Матричное уравнение (1.6) представляет собой однородную систему линейных алгебраических уравнений относительно неизвестных

i. Число неизвестных равно числу уравнений.

16

Система уравнений (1.6) относительно неизвестных i является однородной, поэтому она совместна, однако ее решение является неопределенным, то есть решений бесконечно много. Неопределенность системы обусловлена тем, что строки матрицы P являются линейно зависимыми: на них наложена одна связь, а именно свойство нормированности стохастической матрицы (сумма элементов любой строки равна 1). Поэтому ранг матрицы системы уравнений на единицу меньше числа неизвестных.

Добавив условие нормированности, или линейно независимое уравнение 1

+ 2 + 3 +…+ m = 1, получим систему уравнений, ранг которой равен числу неизвестных. Эта система уравнений является неоднородной, ее решение является единственным. Полученную систему уравнений можно решить известными методами, например, методом Гаусса. Если из системы убрать любое линейно зависимое уравнение, то получим систему m уравнений с m неизвестными, и ее можно решить методом Крамера.

1.9. ВЫЧИСЕНИЕ ПРЕДЕЛЬНЫХ ВЕРОЯТНОСТЕЙ

Приведем две формулы для вычисления предельных вероятностей. Первая формула основана на обращении матриц:

где Pj матрица, полученная из исходной матрицы P вычеркиванием j-й строки и j-го столбца; E единичная матрица; pj j-я строка матрицы P без эле-

мента pjj; e столбец, все элементы которого равны 1.

Исходным уравнением для вывода этой формулы является равенство (1.6).

Запишем это равенство, выделив в нем состояние wj:

где pj – j-й столбец матрицы без элемента jj; π j – строка предельных веро-

ятностей без элемента j. После умножения строки на матрицу получаем новую строку:

( j π j) = ( j ·pjj + π j· pj j · pj + π j·Pj).

Строка в левой и правой части полученного равенства состоит из одного элемента (числа j) и строки π j. Приравняем строки из левой и правой части

Умножим обе части последнего равенства на столбец e справа, все элементы

которого равны 1, что приводит к суммированию элементов строк:

π j·e= j · pj ·(Е – Pj)–1·e.

Прибавим к левой и правой части вероятность j:

π j·e + j = j + j · pj ·(Е – Pj)–1·e.

С учетом условия нормированности имеем: π j·e + j = 1. Поэтому

j (1 + pj ·(Е – Pj)–1·e) = 1,

откуда получаем формулу (1.7): j = 1/ (1 + pj ·(Е – Pj)–1·e).

По формуле (1.7) вычисление каждой предельной вероятности j связано с вычислением обратной матрицы, порядок которой на единицу меньше порядка исходной матрицы.

Замечание. Размеры перемножаемых матриц согласованы.

Вторая формула основана на вычислении определителей и приведена без вывода:

где j = det(E Pj) определитель матрицы E Pj.

По этой формуле предельную вероятность можно вычислить только после вычисления всех определителей и нахождения их суммы.

На практике можно использовать комбинацию этих двух формул. Поскольку предельные вероятности состояний пропорциональны соответствующим определителям, то можно вычислять предельные вероятности состояний без вычисления суммы определителей:

муле (1.7), а k – предельная вероятность любого другого состояния.

1.10.ВЫВОДЫ

1.Переходы между состояниями однородной цепи Маркова описываются

переходными вероятностями, которые удобно записывать в виде матрицы переходных вероятностей.

2. С помощью матрицы переходных вероятностей могут быть получены вероятности состояний на любом шаге в будущем, как при фиксированном начальном состоянии, так и при любом начальном распределении вероятностей состояний.

18

3.Для эргодической однородной цепи Маркова имеют место переходный и установившийся режимы.

4.Для нахождения вероятностей состояний в переходном режиме необходимо начальное распределение вероятностей состояний и матрица переходных вероятностей.

5.Матрица переходных вероятностей достаточна для вычисления предельных вероятностей состояний эргодической цепи Маркова в установившемся режиме.

1.11.ПРИМЕР ЦЕПИ МАРКОВА С ТРЕМЯ СОСТОЯНИЯМИ

Дана цепь Маркова с тремя состояниями, граф состояний которой приведена на рис. 1.8. Как и ранее, вероятности pii на графе не показаны. Ограничимся вычислением предельных вероятностей состояний.

p2

w1 q3

q1 p1

p3

w2 w3

Рис. 1.8. Граф состояний цепи Маркова с тремя состояниями

Матрица переходных вероятностей имеет вид:

Необходимое условие правильного составления матрицы переходных вероятностей выполняется: |E – P| = 0.

Приведем матрицы Pi, в которых вычеркнуты i-я строка и i-й столбец, и оп-

ределители i = |E – Pi|, необходимые для вычисления предельных вероятностей по формуле (1.8):

Сумма определителей:

= 1 + 2 + 3 = p1·p2 + p1·p3 + p2·p3 + p3·q1 + p2·q3 + q1·q3.

Значения предельных вероятностей, вычисленные с помощью определите-

лей: 1 = 1/Δ = 0,302; 2 = 2/Δ = 0,660; 3 = 3/Δ = 0,038.

Видно, что распределение предельных вероятностей является стохастиче-

ским: 1 + 2 + 3 = 1.

20