651_Zelentsov_B.P._Matrichnye_modeli_funktsionirovanija_

Глава 2. ОДНОРОДНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ

2.1.ПОНЯТИЕ ДИСКРЕТНОГО СЛУЧАЙНОГО ПРОЦЕССА В НЕПРЕРЫВНОМ ВРЕМЕНИ

Пусть имеется некоторая система, множество состояний которой являет-

ся дискретным (конечным или счетным): W = {w1, w2, w3, … }. События, приводящие к переходу системы от состояния к состоянию, являются случайными и происходят в непрерывном времени. Таким образом, с течением времени система случайно переходит от состояния к состоянию. Этот процесс описывает эволюционирование вероятностной системы в непрерывном времени, заключающееся в случайных переходах от состояния к состоянию. Изменения состояний происходят случайно, поэтому имеет место случайный процесс изменения состояний во времени, то есть дискретный случайный процесс в непрерывном времени.

Обозначим через S(t) состояние системы в момент времени t. Запись S(t) =

wj означает, что в момент времени t система находится в состоянии wj. Непо-

средственный переход из состояния wi в состояние wj будем, как и ранее, обо-

значать wi wj.

В каждый момент времени система может находиться в одном состоянии. Примеры дискретных случайных процессов в непрерывном времени:

1.Функционирование технической системы, во время которого происходят отказы элементов, простои, профилактическое обслуживание и др. Очевидно, что события, происходящие при функционировании системы, являются случайными.

2.Функционирование системы массового обслуживания, например, системы пожаротушения в большом городе, где каждый пожар начинается в случайный момент времени, а мероприятия по пожаротушению продолжаются случайное время.

Марковский процесс относится к классу случайных процессов с дискретными состояниями в непрерывном времени.

2.2.ИНТЕНСИВНОСТИ ПЕРЕХОДОВ МЕЖДУ СОСТОЯНИЯМИ

Марковским называется случайный процесс, вероятности состояний которого в любой момент времени в будущем определяются состоянием в настоящий момент и не зависят от состояний в прошлом. Переходы от состояния к состоянию будем описывать интенсивностями переходов.

Интенсивностью ij(t) перехода из состояния wi в состояние wj в момент времени t называется условная плотность вероятности непосредственного пере-

хода из состояния wi в состояние wj в момент времени t при условии, что до

21

этого перехода система находилась в состоянии wi, то есть до этого момента времени смены состояния wi не произошло: ij(t) = fij(t)/qii(t), где fij(t) – плотность распределения времени перехода wi wj; qii(t) – вероятность того, что на интервале времени [0, t] система находилась в состоянии wi.

Замечание. Если непосредственный переход wi wj является невозмож-

ным, то ij(t) = 0.

Таким образом, каждая пара состояний (wi, wj), i j, описывается интенсивностью ij(t).

2.3. ПОНЯТИЕ ОДНОРОДНОГО МАРКОВСКОГО ПРОЦЕССА. ГРАФ СОСТОЯНИЙ

Однородным марковским процессом называется дискретный случайный

процесс в непрерывном времени, если интенсивности ij(t) не зависят от времени:

ij(t) = ij, i, j = 1, 2, 3, …, i j.

Смысл свойства однородности заключается в том, что причины, обуславливающие переходы между состояниями и средние продолжительности нахождения в состояниях, не изменяются с течением времени; характер протекания процесса на некотором интервале времени зависит только от длины этого интервала и не зависит от положения этого интервала на оси времени (или от начала отсчета этого интервала). Однородный марковский процесс – это один из простых, но в то же время один из часто применяемых для моделирования реальных процессов.

Замечание. Если интенсивности переходов зависят от времени, то такой процесс будет неоднородным.

Каждое состояние wi однородного марковского процесса характеризуется параметром i, который называется интенсивностью выхода из этого состоя-

тенсивностей непосредственного перехода из состояния wi в другие состояния.

Полагается, что интенсивности выхода i являются ограниченными величинами.

В дальнейшем используется параметр ii, равный интенсивности выхода из

Однородный марковский процесс обладает свойствами ординарности и отсутствием последействия.

22

Свойство ординарности заключается в том, что вероятность хотя бы двух изменений состояния марковского процесса на бесконечно малом интервале времени является бесконечно малой величиной более высокого порядка малости по сравнению с длиной этого интервала, независимо от состояния процесса в начальный момент времени. Другими словами, за бесконечно малый интервал времени не может произойти более одного перехода из состояния в состояние.

Отсутствие последействия заключается в том, что будущее системы (процесса) зависит только от настоящего, оно не зависит от прошлого, то есть не зависит от того, каким путем система эволюционировала из прошлого в настоящее. Следовательно, можно сказать, что при фиксированном настоящем будущее и прошлое системы независимы. Свойство отсутствия последействия называют еще марковским свойством.

Как и в случае марковской цепи, марковский процесс изображают в виде ориентированного графа, вершинами которого являются состояния, а ребрами (стрелками) – непосредственные переходы между состояниями. Каждому переходу приписывается соответствующая интенсивность. Если стрелка отсутствует, то соответствующая интенсивность перехода между двумя состояниями равна нулю, то есть соответствующий непосредственный переход между состояниями является невозможным.

На рис. 2.1 приведен граф из трех состояний. Множество состояний системы

W = {w1, w2, w3}.

λ12 λ23

w1 w2 w3

λ21

λ31

Рис. 2.1. Граф процесса из трех состояний

2.4. РАСПРЕДЕЛЕНИЕ ВРЕМЕНИ НАХОЖДЕНИЯ В ОДНОМ СОСТОЯНИИ

Найдем распределение времени нахождения в состоянии wi при условии,

что это состояние является начальным. Обозначим через qii(t) вероятность того,

что в течение времени t состояние wi не изменится:

qii(t) = p[S(t) = wi / S(0) = wi и не было выхода из wi].

Замечание. Вероятность qii(t) не следует смешивать с вероятностью pii(t), которая будет использоваться позже.

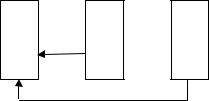
Рассмотрим процесс на интервале времени [0, t + dt]. На рис. 2.2 показана

часть графа состояний, относящаяся к состоянию wi и интервал времени

[0, t + dt].

23

Рис. 2.2. Интервал времени [0, t + dt] и часть графа состояний,

относящаяся к состоянию wi

Очевидно:

qii(t + dt) = qii(t)( 1 + ii dt),

где qii(t) – вероятность того, что в момент времени t система находится в со-

стоянии wi; 1 + ii dt – вероятность того, что на интервале [t, t + dt] выход из wi не произойдет при условии, что в момент времени t система находится в со-

Для того чтобы решить это дифференциальное уравнение, разделим пере-

менные: dqii(t)= ii dt. Проинтегрируем: ln qii(t) = iit + с. Из начального усло- qii(t)

Смысл полученного результата: qii(t) есть вероятность того, что случайное вре-

мя нахождения в состоянии wi превысит значение t. Тогда функция распреде-

ления Fii(t) и плотность распределения fii(t) времени нахождения в состоянии wi имеют вид:

Таким образом, время, в течение которого система находится в каком-либо состоянии однородного марковского процесса, распределено по показательному закону. Математическое ожидание и среднее квадратическое отклонение вре-

Замечания. 1. Показательное распределение времени нахождения в одном состоянии – это единственное распределение, при котором интенсивность на-

2. При распределениях, отличных от показательного, интенсивность наступления события зависит от времени, а случайный процесс не является однородным (это легко показать на примере равномерного или нормированного нормального распределения).

2.5. КЛАССИФИКАЦИЯ СОСТОЯНИЙ МАРКОВСКОГО ПРОЦЕССА

Классификация состояний марковского процесса производится аналогично классификации состояний марковской цепи: состояния классифицируются на достижимые, сообщающиеся, множество существенных и несущественных состояний, поглощающие состояния, эргодическое множество состояний. Напомним, что классификация состояний может быть произведена по графу состояний.

Состояние wj достижимо из состояния wi, если за некоторое конечное время система может перейти из wi в wj, то есть существует такое t, что pij(t) > 0, где pij(t) – вероятность того, что S(t) = wj при условии, что начальным является состояние wi: pij(t) = p[S(t) = wj / S(0) = wi]. Состояние wj не достижимо из состояния wi, если при всех t вероятность pij(t) = 0.

Два состояния wi и wj называются сообщающимися, если они взаимно достижимы, то есть существуют такие t1 и t2, что pij(t1) > 0 и pji(t2) > 0. Все состояния множества сообщаются между собой, если для любой пары состояний wi и wj выполняются эти условия.

Состояние wi является несущественным, если имеется по крайней мере одно состояние wj, достижимое из wi, такое, что wi не достижимо из wj. Состояние wi

называется существенным, если любое состояние, достижимое из wi, сообща-

ется с wi.

Таким образом, состояния системы можно разбить на множество существенных и на множество несущественных состояний. Из множества несущественных состояний (то есть из любого состояния этого множества) система может перейти в множество существенных состояний за конечное время. Однако, перейдя в множество существенных состояний, система никогда из него не выйдет.

Для однородного марковского процесса справедлива теорема:

Если U – множество несущественных состояний, то для любых ui U,

uj U:

lim pU (i, j,t) = 0,

t

где pU (i, j,t) – вероятность того, что в момент t времени система будет нахо-

диться в состоянии uj до выхода из U при условии, что состояние ui является начальным.

25

Смысл теоремы. Если начальным является несущественное состояние, то с течением времени нахождения в других несущественных состояниях этого подмножества стремятся к нулю при t , то есть при t сиcтема выйдет из множества U.

Эргодическое множество состояний – это множество существенных сообщающихся состояний. Из любого состояния этого множества можно попасть в любое другое состояние этого же множества. Система, попадающая в эргодическое множество, никогда его не покидает. Эргодическое состояние является элементом эргодического множества.

Если эргодическое множество состоит из одного состояния, то это состояние

называется поглощающим. После попадания в поглощающее состояние wi система из него никогда не выходит. Для поглощающего состояния интенсивность

выхода i = 0, а вероятности pii(t) = 1 и pij(t) = 0 для всех i j. Марковский процесс с поглощением – это процесс, множество состояний которого содержит хотя бы одно поглощающее состояние.

2.6. МАТРИЦА ИНТЕНСИВНОСТЕЙ

Матрица интенсивностей = ij – это матрица интенсивностей переходов однородного марковского процесса; ее называют еще квазистохастической матрицей, инфинитезимальной матрицей, инфинитезимальной матрицей вероятностей перехода, инфинитезимальной производящей матрицей процесса, инфинитезимальным оператором.

Правило составления матрицы интенсивностей:

1) элемент ij (i j) равен интенсивности непосредственного перехода wi wj;

2)элемент ij (i j) равен нулю, если непосредственный переход wi wj является невозможным;

3)диагональный элемент ii равен сумме недиагональных элементов i-й

Таким образом, сумма элементов любой строки матрицы интенсивностей равна нулю: ij = 0. Это свойство в матричном виде:

Замечание. После составления матрицы интенсивностей целесообразно сделать проверку условия |Λ| = 0.

26

2.7.ВЕРОЯТНОСТИ СОСТОЯНИЙ ОДНОРОДНОГО МАРКОВСКОГО ПРОЦЕССА

Вкачестве вероятностной характеристики однородного марковского про-

цесса вводится условная вероятность того, что в момент времени t система бу-

дет в состоянии wj при условии, что в момент времени t = 0 она находилась в состоянии wi для любых i и j:

pij (t) = p[S(t) = wj / S(0) = wi].

Замечание. Эти вероятности называют иногда переходными вероятностями марковского процесса.

Задача нахождения вероятностей pij(t) решается с помощью дифференциальных уравнений. Составим дифференциальные уравнения вероятностей состояний.

Имеются две взаимно исключающие (несовместные) возможности находить-

ся в состоянии wj в момент времени t + dt:

1) в момент времени t система уже находится в состоянии wj и в течение времени dt это состояние не изменится; соответствующая вероятность равна

pij(t)(1+ jjdt), где jj – интенсивность выхода из состояния wj, взятая со знаком минус;

2) в момент времени t система находится в одном из состояний wk (k j) и за время dt совершает переход wk wj; вероятность этого

Поскольку эти возможности несовместны, то вероятность состояния wj в момент времени t + dt равна сумме их вероятностей:

Внесем второе слагаемое в правой части под знак суммы:

pij (t + dt) = pij (t) + pik (t) kj dt. k

Преобразуем полученное равенство:

pij (t + dt) pij (t) = dt pik (t) kj ;

где p ij (t) производная вероятности pij (t).

27

Уравнения вида

называются уравнениями А.Н.Колмогорова (или Колмогорова Чепмена). Их

можно составить для любой пары состояний wi и wj. Если множество состояний является конечным и число состояний равно m, то можно составить m2 таких уравнений.

Смысл этого результата: получена система дифференциальных уравнений, решение которых дает вероятности состояний однородного марковского процесса как функции времени при заданном начальном состоянии. Эта система дифференциальных уравнений составлена так, что каждое состояние может

быть начальным. При начальном состоянии wi получаем систему из m дифференциальных уравнений.

Замечания. 1. Еще раз отметим, что свойство отсутствия последействия однородного марковского процесса проявляется в том, что вероятности

pij (to, to + t) = p[S(to + t) = wj / S(to) = wi]

не зависят ни от начального момента времени to, ни от течения процесса до момента времени to, то есть

pij (to, to + t) = pij (0, t to).

2. Марковским можно назвать случайный процесс, вероятности состояний которого в любой момент времени в будущем определяются состоянием в настоящий момент и не зависят от состояний в прошлом.

Если число состояний марковского процесса не велико, то система дифференциальных уравнений может быть составлена по специальному правилу. Для формулирования этого правила в дифференциальных уравнениях

А.Н.Колмогорова вынесем слагаемое pij(t) jj из-под знака суммы, обозначив

jj = j:

где j интенсивность выхода из состояния wj.

Специальное правило составления дифференциальных уравнений формулируется следующим образом: производная вероятности состояния равна сумме произведений вероятностей других состояний, умноженных на интенсивности переходов в это состояние, минус вероятность этого состояния, умноженная на суммарную интенсивность выхода из него.

Замечание. При составлении и решении системы дифференциальных уравнений следует учитывать условия неотрицательности и нормированности, которым удовлетворяет однородный марковский процесс:

а) pij(t) 0; б) pij(t)= 1. j

28

2.8. МАТРИЧНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ИХ РЕШЕНИЕ

Будем записывать вероятности состояний pij(t) в виде матрицы:

P(t) = pij(t) . Тогда уравнения (2.6) можно записать в матричном виде:

где P (t) – матрица, каждый элемент которой равен производной соответствующего элемента матрицы P(t).

В этом матричном уравнении для каждой i-й строки может быть написана система дифференциальных уравнений при начальном состоянии wi. Поэтому данное матричное уравнение содержит столько начальных состояний, сколько состояний имеет система.

Перейдем теперь к рассмотрению процесса при заданном распределении на-

чальных вероятностей состояний. Начальная вероятность pi(0) состояния wi – это вероятность того, что в начале процесса, то есть в начальный момент вре-

мени, система находится в состоянии wi: pi(0) = p[S(0) = wi]. Будем записывать начальные вероятности состояний в виде распределения (строки):

p(0) = p1(0) p2(0) p3(0) … pm(0) .

Если начальным является одно определенное состояние wi, то элемент, со-

ответствующий этому состоянию, равен 1, то есть pi(0) =1, а остальные элементы равны нулю. Например, если начальным является первое состояние, то

p(0) = 1 0 0 0 … .

Распределение начальных вероятностей состояний является стохастическим, то есть оно обладает свойствами неотрицательности и нормированности:

pi(0) 0; p(0) e= pi(0) 1 i

для всех i, где e– столбец, все элементы которого равны 1.

Умножим матричное уравнение (2.8) на строку начальных вероятностей: p(0)P (t) = p(0)P(t) .

вероятностей.

Итак, для нахождения вероятностей состояний однородного марковского процесса на некотором множестве состояний следует составить и решить систему дифференциальных уравнений А.Н.Колмогорова, которая может быть записана в двух вариантах:

1) с помощью матрицы вероятностей состояний P (t) = P(t) при начальных условиях P(0) = E, где E – единичная матрица;

29

2) с помощью строки вероятностей состояний p (t) = p(t) при начальном условии p(0).

Различие между этими двумя видами матричных уравнений заключается в том, что в первом случае решение находится в виде матрицы P(t), в котором любое состояние может быть начальным, а во втором случае решение находится в виде строки p(t) с начальными условиями, заданными начальным распределением p(0).

Правило составления уравнений Колмогорова в матричной форме:

1.Составить матрицу интенсивностей .

2.Записать матричное дифференциальное уравнение P (t) = P(t) или p (t) = p(t) .

Одним из возможных путей решения матричных дифференциальных уравнений является применение преобразования Лапласа, то есть решение уравнений операторным методом. Применим к полученным матричным дифференциальным уравнениям преобразование Лапласа, имея в виду, что x(s) x(t) и sx(s) x(0) x (t), где s – комплексная переменная преобразования Лапласа. Прямое и обратное преобразования Лапласа приведены в табл. 2.1.

Табл. 2.1. Преобразования Лапласа исходных матричных уравнений

Система дифференциальных уравнений А.Н.Колмогорова имеет единственное решение при заданных начальных условиях.

Оба вида матричной системы дифференциальных уравнений могут быть использованы для нахождения вероятностей состояний как на множестве существенных, так и как на множестве несущественных состояний. При стохастическом начальном распределении p(0) для множества существенных состояний матрица P(t) и строка p(t) также являются стохастическими (обладают свойствами неотрицательности и нормированности), а для множества несущественных состояний их стохастичность нарушается.

30