
Gurtov_TE
.pdf3.2. Заряд в области пространственного заряда
Одной из основных задач при анализе области пространственного заряда полупроводника является нахождение связи между электростатическим потенциалом ψ(x), с одной стороны, и величинами заряда в области пространственного заряда Qs, избытка электронов и дырок Γp,n, емкости ОПЗ Cs – с другой. Нахождение этой связи основано на решении уравнения Пуассона для ОПЗ.
3.2.1. Уравнение Пуассона для ОПЗ
Запишем уравнение Пуассона для полупроводника p-типа:
d 2ψ |
= − |
ρ (x) |
. |
(3.6) |
dz2 |
|
|||
|
ε 0εs |
|
||
Величина ρ(x) в общем случае, когда отсутствует ограничение на малость возмущения, будет:
ρ (z) = q(ND+ − NA− + p − n) . |
(3.7) |
В квазинейтральном объеме, где условие электронейтральности выполняется, ρ(x) = 0.
Тогда
|
|
|
|
ND+ − NA− |
|
= n0 − p0 . |
(3.8) |
|||||||||||
Поскольку, как было показано в (3.3 – 3.5), |
|
|
|
|
||||||||||||||
|
|
|
n = n0eβϕ , |
|
p = p0e− βϕ , |
|
|
|
||||||||||
для ρ(z) в ОПЗ имеем: |
n0 = ni e− βϕ0 , |
|
|
p0 = pi eβϕ0 , |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ρ (x) = −qp [e−2βϕ0 |
(eβψ −1) − e− βψ + 1] . |
(3.9) |
|||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя (3.9) в (3.6), имеем для нахождения ψ(z) дифференциальное |
||||||||||||||||||
уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2ψ |
= |
qp0 |
[e−2βϕ0 (eβψ − 1) − e− βψ + 1] . |
(3.10) |
|||||||||||||
|
dz2 |
|
||||||||||||||||
|
|
|
εsε 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Домножим выражение для дебаевской длины экранирования, которое |
||||||||||||||||||
представлено в разделе 2.5 формулой (2.23), слева и справа на величину |
|
dψ |
. |
|||||||||||||||
|
|
|||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dψ |
|
|
d 2ψ |
|
|
1 d dψ |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
. |
(3.11) |
|||
|
|
|
|
dz |
|
dz2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 dz dz |
|
|
|
|
||||||
Следовательно,
81

|
|
|
|
dψ 2 |
|
|
|
|
qp |
|
−2 |
βϕ |
|
|
|
βψ |
|
|
|
|
− |
βψ |
|
|
|
|||||||||||||
|
|
|
d |
|
|
|
|
|
= |
|
|
0 |
[e |
|
|
0 (e |
|
|
|
|
− 1) − e |
|
|
+ 1]dψ . |
(3.12) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
dz |
|
|
|
|
|
εsε 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Проинтегрировав (3.12) от бесконечности до некоторой точки ОПЗ, по- |
||||||||||||||||||||||||||||||||||||||
лучаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dψ |
2 |
qp 1 |
|
[(e |
− βψ |
+ βψ − 1) + e |
−2 |
βϕ |
|
(e |
βψ |
|
|
|||||||||||||||||||||||||
|
|
|
= |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
− βψ − 1)]. |
(3.13) |
||||||||||||||||||
|
εsε 0 β |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Воспользовавшись определением дебаевской длины экранирования LD |
||||||||||||||||||||||||||||||||||||||
(2.23), а также соотношением E(z) = − |
dψ |
|
, получаем: |
|
|
|||||||||||||||||||||||||||||||||
dz |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
E2 = |
kT |
|
|
|
|
|
[(e− βψ |
+ βψ − 1) + e−2βϕ0 (eβψ |
− βψ − 1)] . |
(3.14) |
||||||||||||||||||||||||||||
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||
Обозначим |
q |
|
|
|
LD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
F(ψ ,ϕ 0 ) ≡ [(e− βψ |
+ βψ − 1) + e−2βϕ0 (eβψ − βψ − 1)]12 . |
(3.15) |
|||||||||||||||||||||||||||||||||||
Из (3.14) и (3.15) имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
E |
= − |
dψ |
|
= ± |
kT |
1 |
|
F(ψ ,ϕ0 ) . |
|
(3.16) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
LD |
|
|
|
|
|
|
|
||||||
Соотношение (3.16) называется первым интегралом уравнения Пуассо-
на.
Знак электрического поля выбирается в зависимости от знака поверхностного потенциала. Если ψs > 0 (обеднение основными носителями или инверсия), поле направлено вглубь полупроводника по оси z и положительно. При ψs < 0 поле E направлено против оси z и отрицательно.
Величина электрического поля на поверхности Es будет:
E |
s |
= ± kT |
2 |
F(ψ |
,ϕ |
) . |
(3.17) |
|
|||||||
|
q |
|
s |
0 |
|
|
|
|
|
LD |
|
|
|
||
Поскольку согласно теореме Гаусса величина электрического поля на поверхности Es связана определенным образом с плотностью пространственного заряда на единицу площади Qsc, имеем:
Qsc = ε sε 0 Es = ± |
2ε sε 0 kT |
F(ψ s ,ϕ 0 ) . |
(3.18) |
|
qLD |
||||
|
|
|
Отметим, что соотношения (3.16 – 3.18), полученные в этом разделе, являются очень важными и будут в дальнейшем неоднократно привлекаться для анализа ОПЗ.
82

3.2.2. Выражение для заряда в ОПЗ
Выражение (3.18) для заряда в ОПЗ, полученное в предыдущем параграфе, справедливо для любых значений поверхностного потенциала. Однако использование его для конкретных случаев довольно затруднено в силу громоздкости функции F(ψ, φ0) в виде (3.15). Получим выражение для заряда Qsc, упростив соотношение (3.18) для различных областей.
Область обогащения (ψs < 0). Для полупроводника p-типа заряд в ОПЗ Qsc обусловлен зарядом свободных дырок Qp, как только
|
ψ s |
|
> kT |
; |
|
βψ s |
|
|
> 1. |
|
|||||||
|
|
|
|
|
|||||||||||||
Q |
= Q |
|
q |
|
2ε |
ε |
|
kT |
e |
− |
βψ s |
|
|||||
|
= |
|
|
|
|||||||||||||
|
|
|
2 . |
(3.19) |
|||||||||||||
p |
|
|
s |
|
0 |
|
|
|
|
||||||||
sc |
|
|
|
|
|
qLD |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Область обеднения (φ0 > ψs > 0). Заряд в ОПЗ Qsc обусловлен только зарядом ионизованных акцепторов QB. Из (3.16, 3.18) следует, что
Q |
= Q |
|
= |
2ε |
ε |
|
qN |
|
kT |
= |
2ε |
ε |
|
kT |
(βψ |
|
1 |
|
. (3.20) |
|
B |
0 |
ψ − |
|
|
s |
|
0 |
|
s |
− 1) |
2 |
|||||||||
sc |
|
|
s |
|
|
A |
q |
|
|
qLD |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ширина обедненной области
W = |
Q |
|
= |
2ε |
ε |
|
|
|
− |
kT |
|
|
B |
s |
|
0 |
ψ |
|
. |
||||
|
qNA |
|
qNA |
|
s |
|
q |
|
|||
|
|
|
|
|
|
||||||
Область слабой инверсии (2φ0 > ψs > φ0). Заряд в ОПЗ Qsc, так же как и в случае обеднения, обусловлен только зарядом ионизованных акцепторов QB, поскольку заряд свободных электронов Qn << QB.
Q |
= Q |
B |
= |
2ε |
ε |
0 |
qN |
A |
(ψ |
s |
− kT ) = |
2ε sε 0 kT (βψ |
s |
− 1) 12 |
. (3.21) |
sc |
|
|
s |
|
|
|
q |
qLD |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Область сильной инверсии (ψs > 2φ0). Заряд в ОПЗ Qsc обусловлен в ос-
новном зарядом свободных электронов вблизи поверхности в инверсионном канале Qn, хотя в начале области сильной инверсии еще существен вклад заряда ионизованных акцепторов
Qsc = QW + QB ≈ Qn = |
ε sε 0 kT |
e |
β (ψ s −2ϕ0 ) |
. |
(3.22) |
2 |
|||||
2qLD |
|
||||
|
|
|
|
|
Величина заряда ионизованных акцепторов QB в ОПЗ и ширина слоя обеднения W не зависят от поверхностного потенциала ψs и равны:
QB = 2qε sε 0 NA (2ϕ 0 |
− kT ); W = |
2qε sε 0 |
(2ϕ 0 |
− kT ) . (3.23) |
|
q |
qNA |
|
q |
Отметим, что, как следует из рисунка 3.2 и выражений (3.19 – 3.22), область обогащения по многим параметрам подобна области сильной инверсии,
83
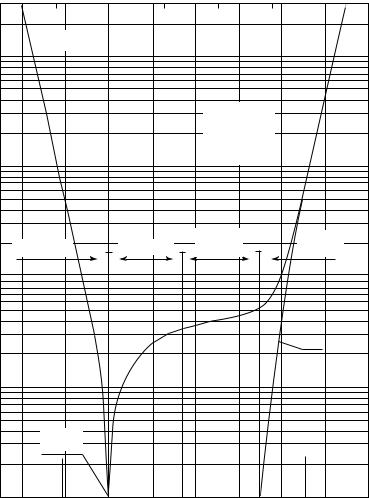
а область обеднения – области слабой инверсии. На рисунке 3.3 приведено |
||||||||
значение заряда в ОПЗ Qsc как функции поверхностного потенциала ψs, рас- |
||||||||
считанное для конкретного случая. |
|
|
|
|
|
|||
|
-10 |
0 |
10 |
|
20 |
30 |
40 |
|
|
|
|
|
|
|
|
βψs |
|
|
QSC, Кл/см2 |
|
|
|
|
|
|
|
10-5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
NA = 1016 см-3 |
|
|
|
|
|
|
|
|
T = 290 K |
|
|
|
|
|
|
|
|
ϕ0 = 0,35 B |
|
|
|
10-6 |
|
|
|
|
2βϕ0 = 28 |
|
|
|
|
|
|
|
|
|
|
|
|
Обогащение |
|
Обеднение |
Слабая |
|
Сильная |
|
||
|
инверсия |
|
инверсия |
|
||||
10-7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
QW |
|
10-8 |
|
|
|
|
|
|
|
|
|
Плоские |
|
|
|
|
|
|
|
|
зоны |
|
|
|
|
|
|
|
|
EV |
|
Ei |
|
|
|
EC |
ψs, В |
10-9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,4 |
-0,2 |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
|
Рис. 3.3. Зависимость заряда в ОПЗ от поверхностного потенциала ψs, рассчитанная |
||||||||
для кремния p-типа |
|
|
|
|
|
|
|
|
3.2.3. Избыток свободных носителей заряда
Важной характеристикой ОПЗ является значение заряда свободных носителей (электронов или дырок) Qp,n или, если выразить этот заряд в единицах
84

элементарного заряда, величина избытка электронов или дырок Γp,n в ОПЗ. Определим величину Γp как
∞ |
|
Γ p = ∫( p(z) − p0 )dz , |
(3.24) |
0 |
|
где p(z) – концентрация дырок в ОПЗ, p0 – концентрация дырок в квазинейтральном объеме.
Таким образом, избыток электронов или дырок – это избыточное по сравнению с равновесным в нейтральном объеме число свободных носителей на единицу площади ОПЗ. В ряде источников иногда избыток свободных носителей Γp,n называют поверхностной концентрацией. Это не совсем верно, ибо поверхностная концентрация по своему смыслу есть число свободных носителей заряда на единицу объема, рассчитанное на поверхности полупроводника. А избыток Γp,n есть избыточное число свободных носителей, проинтегрированное по глубине ОПЗ и рассчитанное на единицу площади.
Из (3.24) следует, что
Γ p = p0 |
∞ |
(e− βψ |
− 1)dz = p0 |
0 |
e− βψ − 1 |
dψ . |
(3.25) |
||
∫ |
∫ |
|
|||||||
|
|
|
|
dψ |
|
||||
|
0 |
|
|
ψ s |
|
|
|
|
|
|
|
|
|
dz |
|
||||
|
|
|
|
|
|
|
|||
Аналогично избыток электронов Γn равен:
|
0 |
eβψ − 1 |
|
|
Γ n = n0 |
∫ |
dψ |
dψ . |
(3.26) |
|
|
ψ s
dz
Понятиями избытка Γp,n чаще пользуются, когда говорят о свободных носителях в инверсионном канале. Для случая обогащения выражения (3.25, 3.26), рассчитанные с учетом (3.15), при значениях |βψs| > 3 будут иметь вид:
|
|
ε sε 0 kT |
− βψ |
|
||
Γ p |
= |
e 2 , |
(3.27) |
|||
2q2 LD |
||||||
|
|
|
|
|||
|
|
ε s |
ε 0 kT |
βψ |
|
|
Γ n |
= |
e 2 . |
(3.28) |
|||
2q2 LD |
||||||
|
|
|
|
|||
Для области слабой и сильной инверсии выражение для Γp,n можно получить в аналитическом виде из выражений для зарядов в ОПЗ, не прибегая к интегрированию (3.25, 3.26).
Действительно, заряд свободных носителей, например, электронов, в инверсионном канале Qn равен разности полного заряда Qsc и заряда ионизованных доноров QB, для которых имеются аналитические выражения:
Qn = Qsc − QB . |
(3.29) |
85

Для случая инверсии соотношение (3.18) для Qsc упростится и будет иметь вид:
|
|
|
|
12 |
(3.30) |
Qsc = 2qε sε 0 NA ψ s + kT (eβ (ψ s −2ϕ 0 ) − 1) |
. |
||||
|
|
q |
|
|
|
Используя выражения для QB в виде (3.20) и (3.23), получаем соответственно для области слабой и сильной инверсии выражения для Qn в виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
kT eβ (ψ s −2ϕ0 ) |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Q |
n |
= |
|
2qε |
ε |
0 |
N |
|
ψ |
s |
− |
|
|
|
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
− 1 |
, |
|
(3.31) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
s |
|
|
|
A |
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
q ψ s − |
kT |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
2ϕ |
|
− |
kT |
12 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
kT e(ψ s −2ϕ0 ) |
|
|
|
q |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||||||||||||||
Q |
n |
= |
|
2qε |
ε |
0 |
N |
ψ |
s |
− |
|
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
s |
|
|
|
A |
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
q ψ s |
|
kT |
|
|
|
|
|
|
|
− kT |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
ψ s |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для случая (3.32), используя соотношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.32) |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1+ x) 12 |
|
≈ 1+ |
x |
|
, |
|
при x << 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
получаем:
Здесь CB = − ∂QB
∂ψ
|
Q |
n |
|
= C |
B |
kT |
e |
β (ψ s −2ϕ0 ) |
. |
(3.33) |
|||||
|
|
q |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
2qε |
ε |
0 |
N |
A |
|
|
|
|
|
|||||
= |
|
|
s |
|
|
|
|
– емкость обедненной области. |
|||||||
|
|
|
|
|
kT |
|
|||||||||
|
ψ s |
− |
|
|
|
|
|
|
|
|
|||||
|
|
|
q |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для случая (3.33) удовлетворительная аппроксимация существует только
при β(ψs – 2φ0) > 7 и имеет вид: |
|
β (ψ s −2ϕ0 ) |
|
|
||
1 |
2 e |
. |
(3.34) |
|||
|
|
|||||
Qn = [2kTε sε 0 NA ] |
2 |
|
||||
|
|
|
|
|
||
Отметим, что выражение (3.33) совпадает с соответствующим выражением для Qn в уравнении (3.22). Величина избытка электронов Γn = Qn/q будет для области слабой и сильной инверсии при соответствующих ограничениях равна:
86
|
|
Γ |
n |
= C |
p |
kT eβ (ψ s −2ϕ 0 ) , |
|
(3.35) |
|||||||||
|
|
|
|
|
|
|
q2 |
|
|
|
|
|
|
||||
|
|
kT |
|
|
|
|
|
12 |
|
β (ψ s −2ϕ 0 ) |
|
|
|||||
Γ |
n |
= |
2 |
|
|
ε |
ε |
0 |
N |
|
e |
2 |
|
. |
(3.36) |
||
|
2 |
|
|
||||||||||||||
|
|
|
|
q |
|
s |
|
|
A |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из соотношения (3.36) при значении ψs = 2ϕ0, т.е. для начала области сильной инверсии, можно получить, что для кремния с удельным сопротивлением ρ = (1 10) Ом см величина избытка Γn(ψs = 2ϕ0) = (1091010) см-2. Максимальное значение избытка Γn, достигаемое в ОПЗ, составляет Γn max = (1 2)1013 см-2 и ограничивается пробоем ОПЗ полупроводника.
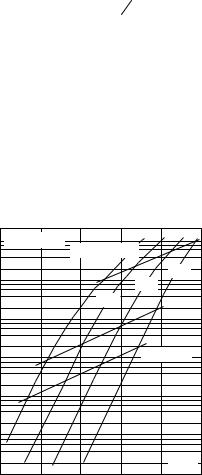
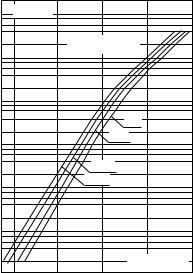
Из соотношений (3.35, 3.36) следует, что избыток свободных носителей экспоненциально зависит от значения поверхностного потенциала ψs и слабо зависит от температуры и легирования полупроводника. На рисунках 3.4 и 3.5 приведены соответствующие графики зависимости Qn и Γn от значения ψs.
10-6 |
Qn, Кл/см2 |
ND = 1014 см-3 |
|
|||
|
|
|
|
|||
10-7 |
|
|
|
|
1017 |
|
|
|
|
|
1016 |
|
|
|
|
|
|
1015 |
|
|
10-8 |
|
|
|
|
|
|
10-9 |
|
|
|
|
βψs = 2ϕ0 |
|
10-10 |
|
|
|
|
|
|
10-11 |
|
|
|
|
|
|
|
|
|
|
|
βψs |
|
10-12 |
|
|
|
|
|
|
15 |
20 |
25 |
30 |
35 |
40 |
|
Рис. 3.4. Зависимость заряда свободных электронов Qn в инверсионном канале от поверхностного потенциала ψs, рассчитанная для кремния p-типа с различной концентрацией акцепторов
87
1013 |
Гn, см-2 |
|
|
|
|
|
NA = 1015 см-3 |
|
|
1012 |
|
|
|
|
1011 |
|
|
|
|
|
|
80 |
|
|
1010 |
|
140 |
|
|
|
|
|
|
|
|
|
230 |
|
|
109 |
|
320 |
|
|
|
|
|
|
|
108 |
|
|
|
|
107 |
|
+β(ψs - 2ϕ0) |
||
|
|
|
|
|
-4 |
0 |
4 |
8 |
12 |
Рис. 3.5. Зависимость избытка электронов Γn в инверсионном канале от поверхностного потенциала ψs, рассчитанная для кремния p-типа при различной температуре
3.2.4. Среднее расстояние локализации свободных носителей от поверхности полупроводника
Для ряда процессов, протекающих в ОПЗ, важной характеристикой является среднее расстояние λc, на котором локализованы свободные носители заряда, электроны или дырки, от поверхности полупроводника. Определим величину λc следующим образом:
∞
∫ ρ (z)zdz
λ |
|
= |
0 |
, |
(3.37) |
c |
∞ |
||||
|
|
|
∫ ρ (z)dz |
|
|
|
|
|
0 |
|
|
где ρ(z) – плотность заряда свободных носителей в направлении, перпендикулярном поверхности.
Очевидно, что интеграл
∞ |
|
∫ ρ (z)dz = Qp,n |
(3.38) |
0 |
|
88
равен заряду свободных носителей в ОПЗ. Для случая обогащения поверхности основными носителями (для полупроводника p-типа – дырками) величина λc будет после соответствующего интегрирования равна:
λc = |
βψ s LD |
. |
(3.39) |
|
F(ψ s ,ϕ 0 ) |
||||
|
|
|
Отметим, что соотношение (3.39) применимо и для случая инверсии, если под λc понимать центроид расположения полного заряда Qsc в ОПЗ.
Для области слабой инверсии электрическое поле E(z) в пределах инверсионного слоя постоянно и равно полю на поверхности Es. Электростатический потенциал линейно спадает по инверсионному слою:
ψ = ψ s − Es z . |
(3.40) |
При этом распределение концентрации n(z) по глубине инверсионного слоя будет:
n(z) = n0eβ (ψ s − Es z ) = ns e− βEs z . |
(3.41) |
Тогда из (3.39) и (3.41) с учетом (3.4, 3.5) и (3.18) следует:
λc = |
1 |
= |
ε sε 0 kT |
. |
(3.42) |
|
βEz |
qQB |
|||||
|
|
|
|
Как следует из (3.42), в области слабой инверсии среднее расстояние λc свободных носителей заряда слабо зависит от поверхностного потенциала ψs, а следовательно, и от избытка свободных носителей в канале. Зависимость λc от температуры T близка к линейной.
Для области очень сильной инверсии, когда Qn >> QB, выражение для центроида электронов в инверсионном канале дается соотношением (3.39). В промежуточной области значений поверхностного потенциала среднее расстояние λc необходимо рассчитывать, пользуясь численными методами, по уравнению (3.37).
На рисунке 3.6 приведен результат такого численного расчета. Обращает
на себя внимание тот факт, что значения центроида λc лежат в пределах (20 300) Å в реально достижимых случаях как для случая обогащения, так и инверсии. Особой точкой является значение потенциала плоских зон ψs = 0, где значение λc равняется дебаевской длине экранирования, достигающей десятых долей микрона.
89

o |
|
|
|
|
|
|
λ, A |
|
|
|
NA = 1015 см-3 |
|
|
|
|
|
|
VSS = 0 |
|
|
250 |
T = 320 K |
|
|
|
|
|
|
|
|
|
|
||
|
290 |
|
ψs = 2ϕ0 |
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
260 |
|
|
|
|
|
150 |
230 |
|
|
|
|
|
|
200 |
|
|
|
|
|
100 |
170 |
|
|
|
|
|
|
140 |
|
|
|
|
|
50 |
110 |
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
Гn, см-2 |
|
|
|
|
|
|
|
|
|
|
107 |
108 |
109 |
1010 |
1011 |
1012 |
1013 |
Рис. 3.6. Рассчитанное численно среднее расстояние локализации электронов λc в ОПЗ в зависимости от избытка электронов Γn при разных температурах. Пунктирная линия соответствует самосогласованному квантовому расчету Стерна для многих уровней при T = 300 К для кремния p-типа
3.2.5. Форма потенциального барьера на поверхности полупроводника
При решении уравнения Пуассона в разделе 3.2.1 нами был получен первый интеграл в виде (3.16). Для нахождения формы потенциального барьера, т.е. зависимости электростатического потенциала ψ(z), необходимо проинтегрировать соотношение (3.16) и получить второй интеграл уравнения Пуас-
сона:
ψ |
dψ |
|
|
kT |
1 |
|
|
||
∫ |
|
= |
z . |
(3.43) |
|||||
F(ψ |
,ϕ |
) |
q |
|
L |
||||
ψ s |
s |
0 |
|
|
|
|
D |
|
|
В общем виде уравнение (3.43) решить и найти аналитическое выражение ψ(z) не удается. Рассмотрим частные случаи.
1. Собственный полупроводник: p = n = ni; φ0 = 0
Из (3.15) следует, что величина F(ψ, φ0) для собственного полупроводни-
ка
|
− βψ |
|
βψ |
|
1 |
|
|
1 |
|
βψ |
|
|
F(ψ ,ϕ 0 ) = (e |
|
+ e |
|
− 2) |
|
2 |
= |
|
sh |
|
. |
(3.44) |
|
|
|
2 |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя (3.44) в (3.43), имеем:
90
