Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

mo-crib-03

.pdf

Скачиваний:

116

Добавлен:

09.02.2015

Размер:

11.29 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

											x3 = 10 - x1 - 2x2								(a)
											x4 = 6 - x1 - x2								(b)
											x4 = 6 - x1 - x2								(b)
													x j	³ 0, j =		1,4
										x1max =5(прибольших x1 начнет
	1ДБР									убыватьфункцияцели)
					f (					64748
							) = 5x +				(5 - x + x )						x + (x - 2x )x					® max
						x	) = 5x +				(5 - x + x )						x + (x - 2x )x				2	® max
								1					1	2				1	1	2	2
										x1max		= 10 (по(а)) при x2 = 0
										x1max		= 6 (по(b)) при x2 = 0
										x1max		= 6 (по(b)) при x2 = 0
	Вводим u1 :
		1	∂f		= (5 - x + x					) = u
					= (5 - x + x				2	) = u
		2 ¶x1						1	2	1
		2 ¶x1
	В 1ДБР мы находим max значение для x1																	и вводим новую переменную.
	Новое ДБР:
											x3 = 5 + u1 - 3x2
											x4 = 5 - u1 - 2x2
											x4 = 5 - u1 - 2x2
											x1		= 5 - u1 + x2
	2ДБР										x1		= 5 - u1 + x2

											x j		³ 0, j = 1,4
											x j		³ 0, j = 1,4
																				® max
					f (x) = (25 + 5x2 ) ×1 + (-u1 )u1 + (5 - x2 )x2															® max
	Начальная таблица по 1ДБР:
Начальная таблица по 1ДБР															Промежуточная таблица									Окончательная таблица
																								(начальная для след.
				1				X 1			X 2				НБП				1	U1			X 2	(начальная для след.

																								НБП		1	U1	X 2
БП															БП									НБП		1	U1	X 2
																								БП
X 3				10				-1			-2				X 3				5	1			-3	БП
X 3				10				-1			-2				X 3				5	1			-3	X	3	5	1	-3

X 4				6				-1			-1				X 4				1	1			-2

																								X	4	1	1	-2
X 1				0				1			0				X 1				5	-1			1	X	4	1	1	-2
X 1				0				1			0				X 1				5	-1			1	X	1	5	-1	1
X 2				0				0			1				X 2				0	0			1	X	1	5	-1	1
X 2				0				0			1				X 2				0	0			1	X	2	0	0	1
1				0				5			0				1				25	-5			5	X	2	0	0	1
1				0				5			0				1				25	-5			5	1		25	0	5

X 1				5				− 1			1				X 1				0	1			0

																								X	1	0	-1	0
X 2				0				1			2				X 2				5	-1			-1	X	1	0	-1	0
X 2				0				1			2				X 2				5	-1			-1	X 2		5	0	-1
																								X 2		5	0	-1

итерации)

Алгоритм

Выбор разрешающего столбца.

Если в lой строке функции цели все(коэфф. при переменных ui )=0 и все(коэфф. при x j )=0, то текущее решение является оптимальным.

Иначе, в качестве разрешающего столбца выбираем любой столбец ui , в которой в lой строке функции ненулевой коэфф.

Если все(коэфф. ui )=0 в lой строке функции или таких столбцов нет, то в качестве разрешающего столбца выбираем любой с переменной x j с положит. коэфф. в lой строке функции цели.

2)Определение разрешающей строки.

Найдем отношение для нижней части таблицы:	с0 j	причем это вычисление выполняется лишь

cjj

тогда, когда cjj 0 ;

cjj -это элемент, стоящий на пересечении разрешающего столбца и главной диагонали нижней части таблицы.

Для верхней части таблицы вычисляем отношение свободных членов к модулям коэфф. из разрешающего столбца.( рассмотрим только для тех строк, где эти коэфф. противоположны по знаку с с0 j ). Сравниваем все найденные отношения. Строка, дающая min из этих отношений,

берется в качестве первой разрешающей строки. 3.Заполнение промежуточной таблицы.

В разрешающем столбце в промежуточной таблице занесена переменная x j из разрешающей

строки начальной таблицы, если эта разрешающая строка находится в верхней части таблицы. А если в нижней(начальная таблица) части, то в разрешающий столбец промежуточной таблицы записываем очередную промежуточную переменную ui .

Все элемента разрешающего столбца делим на генеральный элемент и записываем в промежуточную таблицу. Остальные элементы разрешающей строки делаем равными «не существует». Прочие элементы пересчитываем по обычному правилу прямоугольника.

Строка у нижней части таблицы, которая пересекается с разрешающим столбцом на главной диагонали нижней части таблицы называется 1ой разрешающей строкой.

Если 1ая разрешающая строка находится в нижней части таблицы, то 1ая и 2ая разрешающие строки совпадают.

4) Заполнение конечной таблицы.

Верхняя часть полностью совпадает с верхней частью промежуточной таблицы. На место заглавное переменной во 2ой разрешающей строке конечной таблицы записывается имя переменной из разрешающего столбца промежуточной таблицы. Делим 2ую разрешающую строку промежуточной таблицы на генеральный элемент из начальной таблицы, получаем соответствующую строка в конечной таблице.

Прочая h-ая строка получается, если из hой строки промежуточной таблицы вычесть 2ую разрешающую строку конечной таблицы умноженную на hый элемент из lой разрешающей строки начальной таблицы.

_ 25 -5 5 5(0 -1 0)

250 5

//Если функция цели перестает зависеть от ui , то её можно исключить из рассмотрения.

31. Метод Вульфа.

Этот метод основан непосредственно на рез-ах теоремы Кнута-Такера в

R R

³ 0}

дифференциальной форме. (1) min{f (x) = c t x t Dx / AX = b, x

A = {a

}

ij m×n

...

D – квадратная симметричная матрица размером N×N

Пусть D положительно определена или положительно полуопределена(для гарантии min),тогда совокупность необходимых и недостаточных условий.

		R	R
		R	= b
		Ax	= b
	R	R	R	R
2Dx		-υ + AT x		= -c
(2).		R	³ 0
		x	³ 0
		υ ³ 0
		υ ³ 0

(3).X jυ j = 0, j = 1, n

Вместо (1) будем решать (2) и (3) используя дополнительное правило. Если в текущем базисе есть переменная, Хj , то переменная Vj не должна включаться очередное ДБР и наоборот.

3 этапа решения задачи. 1 этап .- Определить, если это возможн, ДБР для Ax = b

Решается (2 и (3) с целью определить совместимость Ax = b Для этого введем набор искусственных переменных.

	ω1		z1	(1)		z1	(2)
R		R			R
ω = ...		; Z (1)	= ...		; Z (2)	= ...		; μ
				(1)			(2)
	ωт			(1)			(2)
	ωт		zn			zn

будем решать.

= b

И вместо Ax

= b

+ w

= 0

(4.)

2Dx

= v + Aλ + Z 1

- Z ( 2) + μc

³ 0; Z 1

³ 0; Z (2) ³

³ 0; v

0; w ³ 0, μ ³ 0

(5.)...x j v j = 0, j =

1, n

В базис 1ДБР входят все w и часть переменных Z (1)

j , Z ( 2) j

∑ wi ® min при огранич. (4) и (5)

i=1

Вчисле НБП принудительно удерживаем все R λ μ

v, ,

Врезультате получим некоторое ДБР задачи (4), (5) При этом,если все wi уйдут из базы то (1) совместна.

2 этап - Из последнего достигнутого ДБР (4),(5) вычеркнем все столбцы с Wi и все столбцы с НБП Z (1) j , Z ( 2) j .Остановимся в базисе переменного Z (1) j , Z ( 2) j перенумеруемся заново. На втором этапе решаем min задачу вида.

∑ Z j ® min

i=1

При этом принудительно держим в НБП переменную μ .Обязаны обеспечить выполнения ограничения (5)

3 этап.- Надо определить решение задачи для конкретно заданного в-ра С

μ → min

Обязательно выдерживаем ограничение (5).Если не получается сделать ни одной итерации с учетом (5),то функция исходной задачи не ограничена снизу В противном случаи делаем альфа итерации.В результате получаем Мю1 и Мю 2.

x1Rv 1Rλ1μ1

			2
		x
		R
v 2				по этими двумя точкам сможем определить решение при μ = 1
		R2
	λ
	μ 2

Решение определяется по формуле.

μ2 -1

1 - μ1

v 2

μ2 - μ1

μ2

- μ1

μ1

μ 2

x1Rv 1Rλ1μ1

μ2

< 1;

1 - μ1

v 1

μ2

- μ1

λx

μ1

μ = 1

			2			1
		x			x
		R			R
v 2				v 1
		R2		-	R1
	λ				λ
	μ 2				μ1

					λ1
						м.б. любого знака,а
Надо считать в общем случаи компоненты. λ = ...						м.б. любого знака,а
					λт
следовательно в остальных методах(где				³ 0 ) Мю
следовательно в остальных методах(где			λ	³ 0 ) Мю
заменить. λi = λi	(1) - λ( 2) i , λi	(1) ³ 0; λ( 2) i ³ 0 .

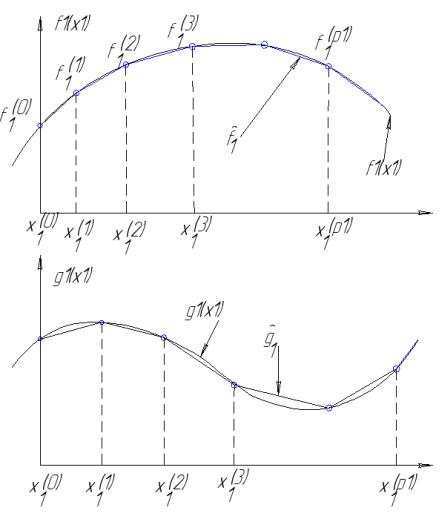
32. Метод кусочно-линейной аппроксимации.

Этот метод надежен,если все функции являются сепарабельными, причем если они выпуклые,а ср. ц. вогнутая,то метод позволяет найти глобальный экстремум, иначе гарантировано нах-ие локального экстремума,в качестве приближения к истинному решению.

		n
1.	f (x) = ∑ f j (x j ) ® max(ксенараб - функция)
1.		j =1
		n
2.		∑ gij (xi ) = bi , i = 1, m
3.		j =1

		x j ³ 0, j = 1, n
		x j ³ 0, j = 1, n

Рассмотрим общ. Схему метода:

Применительно к Х1 проведем аппроксимацию для любой функции,которая зависит от Х1 в виде линейной комбинации значений этих функций.

1.определим отрезок взаимных значений Х1.

2.Разобьем этот отрезок на произвольное число подинтервалов.

На любом из подинтервалов справедливо опред-ии вып-ой и вогнутой функции с исп. ВЛК(Вып. Мин. комбинации)

h( Ax1(3) + (1 - λ)x1( 4) ) £ λh(x1(3) ) + (1 - λ) f (x1(4) )

Применительно к f1 (x1 )

	p1	λ	1
f1 = ∑ f1		λ	1
ˆ	(k )	k
	k =0
ˆ	p1
ˆ	( k )		k	е
g11	= ∑ g11		λ 1	λ − неизвестныепеременны .

k =0

∑λk 1 = 1

k =0

λ(k ) ³ 0, k = 0, p1

Правило.

Для переменной x1 в любом ДБР заменяющей линейной задаче отличными от Ф м.б. одна или две переменных λ1( л) ,соседние по номеру к,а остальные д.б.=1

Мы должны принудительно обеспечивать правило для любых переменных xj C такой моделью мы получим задачу.

n p j

f (λ ) = ∑∑ f j k λ j k ® max

j =1 k =0

n p j

∑∑ gij k λ j k = bi , i = 1, m j =1 k =0

∑λ j (k ) = 1, j = 1, n

k =0

λ j k ³ 0, j = 1, n....., k = o, pi

«+» эту зад. М. решать как обычную линейную задачу, проверил на любой итерации правила.

«-»Размерность зад. Много больше,поэтому,если Хj выходит в исх. зада. Всюду линейна(Сj Xj и AijXj),то по этой переменной не обязательно проводить аппроксимацию,а прямо так включать ее в задачу.

Условия остановки.

1.λ -оптимальноерешение с учетом признаков.

2.Раньше,чем получим λ ,если не удается выполнить требования правила,тогда

λтек ≈ λ принимается за приближенное решение тек. Решения уточняется,проводя разбиение интервалов значения, Хj на более мелкие интервалы в окрестности полученного решения.

Переход к исход.

p j

X j = ∑ x j (k ) λ j (k ) ;…. j=1,n k =0

35. Методы Штрафных функций.

Min f(x) решение такой задачи заменяется на решение бесконечной последовательности

задач безусловной оптимизации следующего вида: min(f (x)+ lim δ k (x | X ))

k −>∞

(

| X ) = δ (

| X ) = 0, "

Î X

lim δk

- идеальная функция штрафа. В зависимости от вида

k →∞

+ ¥, "x Ï X

исходной задачи существуют 2 метода штрафных функций.

1) Метод внутренних штрафных функций (барьерных функций).

δ (

| X ) = 0, "

Î X

+ ¥, "x Ï X

Находим минимум с гарантией, т.к f(x) и δk (

| X ) -

выпуклые.

Задача: min f(x) где f(x) –

выпуклая функция

: gi

(x ) ³ 0 i = 1, m - вогнутые функции т.е - gi (x ) £ 0 -

выпуклая.

(x) ® min при росте

Fk (x, rk ) = f (x ) - rk ∑ ln gi

i=1

k : rk

® 0 + , Fk (

, rk )

= f (

) + rk ∑

® min

k → ∞

i=1 gi (x)

Алгоритм:

(0)

1) x

(0 )

Î X

)> 0 i = 1, m , (??? Некоторое условие остановки???)

внутр

т.е gi (x

2) Решаем последовательность задач безусловной оптимизации

Fk (x, rk ) = f (x ) - rk ∑ln gi

(x ) ® min

(k −1)

(k )

(k −1)

(0)

начинаем из точки

для поиска приближения

, x

,..., x

(k −1)

3) lim x

= x *

→∞

2) Метод внешних штрафных функций

Этим методом удобно решать следующие задачи

f (

) ® min

f (x)- выпуклая

0, "x Î X

(x) £

0 i = 1, m

δ k (x | X ) =

δk (x | X ) = rk Fk

(x | X ) rk ® ¥

> 0, "x Ï X

k →∞

gi (x ) = 0 i = m +1, l

Решение задачи начинается из недопустимой точки x X . Сушествует 2 вида функции штрафа:

		m			2	l		2
Φ1		m			(x))	l
Φ1	(x \| X ) = ∑(gi			+	(x))	+ ∑(gi (x))
		i=1	~	+		i=m+1		~
		i=1				i=m+1
		m	~ +			l	~
			~ +		(x)+ ∑\|		~	(x)\|
Φ2 (x \| X ) = ∑ gi					(x)+ ∑\|		gi	(x)\|
		i=1				i=m+1

~ +	(x)-срезка- функция для	~	(x)отсекающая все
gi		gi

~ +		~
~ +	0, gi (x) £ 0
отрицательные значения: gi	(x) =	~	(x)
		gi	(x)

~ +	~	(x)}
\| gi	(x) = max{0, gi	(x)}

В методе внутренних штрафных функций мА начинаем из x X и никогда из нее не выходим => можем прекратить работу алгоритма на любой итерации, но мы должны для любого ограничения вычислять частные производные и обеспечивать x Î X внутр .

В методе внешних штрафных функций работа начинается из недоступной точки и решаем

задачу F

(

, r

) = f (

) + r Φ

(

| X ) → min; r

→ + ∞ , поэтому решение получается

k → +∞

в пределе при больших к. но зато при любой итерации нужно обрабатывть только

	~			(k )
нарушаемые ограничения	gi	(x			)> 0

Алгоритм:

1)x (0) X , задаем условие остановки

2)решаем последовательность задач бузусловной оптимизации

Fk (x, rk )= f (x)+ rk

∑(gi

(x))

i=1

lim x

(k ) = x *

k →∞

l			→ + ∞
∑(gi		(x)) → min rk	→ + ∞
	~
i=m+1			k →+∞
i=m+1

36. методы случайного поиска В этих задачах намеренно вводится элемент случайного выбора исходных

f (x) → min

параметров.

ζ (k ) - вектор случайных величин.

(k +1) = x(k ) + d

ζ (k )

, k = 0,1,2...

1) Медод случайного поиска с возвратом при неудачном шаге.

(k ) , вычисляем

(k +1) =

(k ) + dζ

(k ) если

f (

(k +1) )< f (

(k ) ) и y(k +1) x то шаг считаем

удачным и x (k +1) = y(k +1) иначе шаг считаем неудачным и остаемся в x (k )

Условие остановки: если x (k ) = x (k +1) = x (k +2) = .. = x (k + N ) то останавливаем алгоритм и считаем x* = x (k )

2)алгоритм наилучшей пробы

Многократная случайная выборка ζ (1),ζ (2 ),...,ζ (m ) - среди них выбирается наилучшая по

правилу: f (

(k ) )+ dζ

(i ) = min f (

(k ) + dζ

(i ) ) и вычисляем

(k +1) =

(k )+ dζ

(i ), d > 0, m > 1

1≤i≤m

3)алгоритм статического градиента.

(1 ) , ζ

(2 ) ,..., ζ

(m ) , оцениваем: f

(k ) = f (

(k ) + γζ

(i ) )− f (

(k ) ), i = 1, m .

m, ζ

(i ) по формуле p(k ) =

(k ) ∙ ζ

(i ) (p- статический градиент дельта ф это

∑ f

Усредняем ζ

i=1

веса случайных векторов). Делаем шаг в направлении статического градиента

x (k +1) = x (k ) + ap(k )

4)алгоритм случайного поиска с покоординатным обучением.

В предыдущих алгоритмах не учитывались результаты предидущих ходов, разумно былобы учитывать , т.е целенаправленно изменить распространение случайных волн => такой алгоритм является само обучающимся.

+ 1свероятностью p

ξ = ξ (

)

ξ (

) = (ξ1 (

w1 ),...,ξn (

n ))T ; ξi

j = 1, n

0, w < −1

− 1c вероятностью (1 − p j )

0.5 ∙ (1 + w

; w

[− 1,1]

1, wj

> 1

Алгоритм:

1)На первом шаге нет обучения т.е x (0) , d , x (1) = x (0) + dξ (w (0) ), w (0) = (0,...,0)T

2)На 2-м шаге тоже нет обучения. x (2 ) = x (1) + dξ (w (1) ), w (1) = (0,...,0)T

3)Начиная с 3-го шага выполняется самообучение алгоритма

x(k +!) = x (k ) + dξ (w (k ) ), k > 1, известны: x(0 ), x(1),..., x(k +1), w (k ) , найдем

wj(k +1) = βw(jk ) − δsign[(f (x(k +1) )− f (x(k ) ))∙ (x(jk ) − x(jk +1) )], j = 1, n вычислим p j и

переходим в точку x (k +2) = x (k +1) + dξ (w (k +!) ) Выбираем сами параметры:

β ³ 0 - параметр интенсивности запоминания предидущего опыта( чем он выше тем сильнее память алгоритма)

δ ³ 0 - параметр скорости обучения (чем он выше тем быстрее обучаемость) Если хоть один из параметров = 0 то алгоритм не обучается

4) Если переход x (k −1) → x (k ) удачен то на очередном шаге вероятность выбора направления (x (k ) − x (k −1) )увеличивается иначе уменьшается .

Билет 37. Постановка общей задачи линейного программирования. Примеры задач.

Общий вид задачи линейного программирования(ЗЛП):

Ту же задачу можно записать в матричном виде:

Где A – матрица k на n, - матрица (m-k) на n, с – вектор из n элементов, b – вектор из k элементов, – вектор из (m-k) элементов.

Канонический вид ЗЛП:

Пример: задача о переменном рационе.

Постановка задачи: составить такой рацион потребления различных продуктов, в котором содержится как минимум суточная потребность в каждом из веществ, минимизируя стоимость.

Билет 38. Свойства решений ЗЛП. Имеем задачу ЛП в общем виде.

Теорема 1 об области определения ЗЛП.

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.09.201999.78 Кб19Ministerstvo_obrazovania_i_nauki_Rossyskoy_Fed....docx
#
09.02.20151.32 Mб107MIPI_DSI_Specification_v1b_8320061508.pdf
#
09.02.20153.63 Mб9MM2 TP.pdf
#
09.02.20158.01 Mб338MNE_Физика и технология микро- и наносистем.pdf
#
09.02.20154.31 Mб9MNG.pdf
#
09.02.201511.29 Mб116mo-crib-03.pdf
#
09.02.2015173.57 Кб8MO_laba_4.doc
#
20.09.20192.79 Mб11mss-crib2.doc
#
09.02.20151.6 Mб7mss-crib2.pdf
#
21.09.20191.05 Mб14mss_answers.doc
#
18.08.2019261.63 Кб0MST 42-51.doc