
mo-crib-03
.pdf
6)Задачи линейного программирования
 ,
,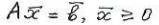 , где
, где
Здесь Х – полиэдр, т.е. |
, или в развернутом виде |
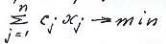 ,
, ;
;
существуют и другие формы записи задач линейного программирования.
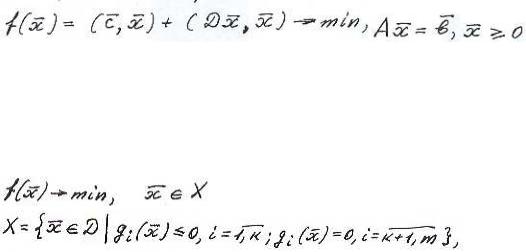
6.Классы задач оптимизации: линейного программирования с примерами,квадратичного программирования,дискретного программирования,оптимального управления.
1)Задачи квадратичного программирования
Здесь Х – полиэдр, т.е. множество, задаваемое линейными условиями. Здесь D – симметрическая неотрицательно-определенная матрица размером n х n, т.е.
 , вектор
, вектор  .
.
2)Задачи дискретной оптимизации(дискретного программирования)
, где
где
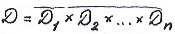 , причем
, причем 
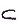



Здесь 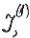 - некоторое подмножество множества
- некоторое подмножество множества 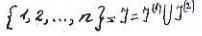 .
.
Если , то имеем задачу целочисленного программирования. 3)Задачи оптимального управления Постановка этих задач сложнее постановки рассмотренных ранее, поэтому рассмотрим сначала содержательный пример.
, то имеем задачу целочисленного программирования. 3)Задачи оптимального управления Постановка этих задач сложнее постановки рассмотренных ранее, поэтому рассмотрим сначала содержательный пример.
Задача о строительстве дороги Требуется проложить дорогу по неровной местности между двумя пунктами. Затраты на
строительство пропорциональны количеству завезенного и вывезенного с трассы грунта. Пусть Т – длина дороги, с(t)- известная высота местности в точке на расстоянии
 от начального пункта трассы. Определить функцию
от начального пункта трассы. Определить функцию 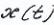 ,
,
описывающую высоту дороги в каждой её точке , при которой затраты на её строительство минимальны. При этом наклон(уклон) дороги в любой точке трассы не
, при которой затраты на её строительство минимальны. При этом наклон(уклон) дороги в любой точке трассы не
должен быть больше  , т.е.
, т.е. . Скорость изменения
. Скорость изменения
наклона дороги не должна превышать константы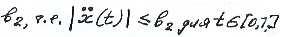 Уровень дороги в начальном и конечном пунктах определяется
Уровень дороги в начальном и конечном пунктах определяется
выражениями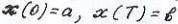 .Тогда математическая формулировка задачи
.Тогда математическая формулировка задачи
такова: минимизировать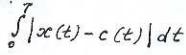 при условиях
при условиях
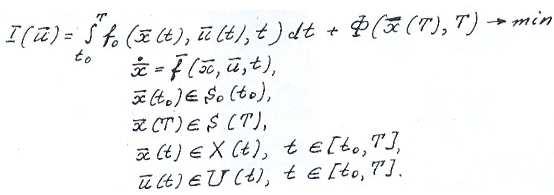
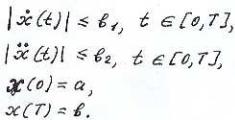 Параметром управления здесь является объем грунта, вывезенный или завезенный в точку трассы на расстоянии t от начального пункта, т.е.
Параметром управления здесь является объем грунта, вывезенный или завезенный в точку трассы на расстоянии t от начального пункта, т.е.
величина, пропорциональная 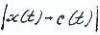 .
.
Перейдем теперь к общей постановке задачи оптимального управления. Движение управляемого объекта описывается системой дифференциальных уравнений
 ,
,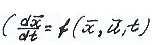 , где
, где 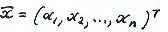 - где
- где
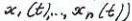 - n-мерный вектор координат расстояния объекта, или фазовые координаты.
- n-мерный вектор координат расстояния объекта, или фазовые координаты.
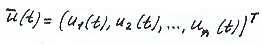 - n-мерный вектор управления. t- время.
- n-мерный вектор управления. t- время.
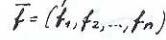 - n-мерный вектор функций.
- n-мерный вектор функций.
Движение объекта подчинено начальным условиям: ,конечным условиям
,конечным условиям  , и ограничениям на фазовые координаты(фазовым
, и ограничениям на фазовые координаты(фазовым
ограничениями) .
.
Кроме того, заданы ограничения на управление:
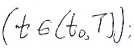 . Здесь
. Здесь  - отрезок времени, на котором происходит
- отрезок времени, на котором происходит
управление системой.  при каждом t - заданные множества из пространств соответствующих размерностей.
при каждом t - заданные множества из пространств соответствующих размерностей.
Итак, в этих задачах в качестве элементов, на которых ведется минимизация, выступают функции. Эти задачи относятся к классу задач оптимизации в бесконечномерных функциональных пространствах. Итак, общая модель такова:
Здесь функционал – это аналог функции цели в конечномерных задачах.
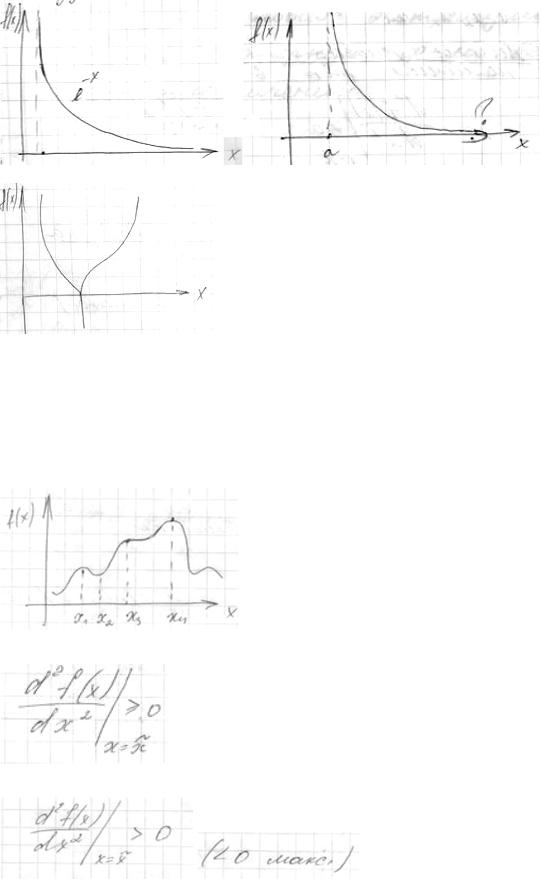
7.Условия экстремума одномерных функций без ограничений.
Стандартные определения локального и глобального решений достаточно нечеткие, и не удовлетворяют например таким функциям: 
Теорема Вейерштрасса(достаточное)
Любая непрерывная функция, заданная на замкнутом ограниченном множестве достигает своего минимума во внутренней или граничной точке множества.
Необходимое условие го порядка минимум функции в точке ~
I- ( x )
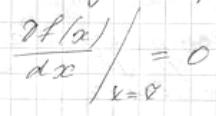 - условие стационарности.
- условие стационарности.
Необходимое условие II-го порядка(наличие min в точке )
)
Достаточное условие II-го порядка(наличие min в точке )
)

Бывает что 2-ая производная = 0, тогда используют аппарат старших производных:
Допустим что в  k производных функции
k производных функции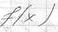 , причем
, причем
 . Если k четное и
. Если k четное и
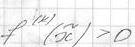 ,то в точке
,то в точке находится локальный минимум функции; если k нечетное,то ничего сказать нельзя.
находится локальный минимум функции; если k нечетное,то ничего сказать нельзя.
8.Условия экстремума многомерных функций без ограничений. Вид знакоопределенности квадратичной формы.
- Необходимое условие
- стационарная точка. Матрица Гёссе:
Если Н неотрицательно определена, т.е. положительно определена или положительно полуопределена, то в исследуемой точке функция является строго выпуклой или просто выпуклой. Если Н неположительно определена, т.е. отрицательно определена или отрицательно полуопределена, то в точке функция строго вогнутая или просто вогнутая.
Рассмотрим общий случай: 
 и разложение в ряд Тейлора эту функцию в точке
и разложение в ряд Тейлора эту функцию в точке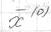 :
:
Перенесем |
в левую часть: |
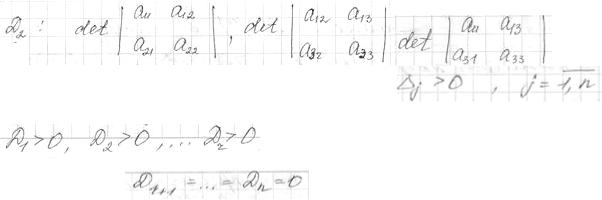
 при
при 
 . Если мы перенесем начало координат в точке
. Если мы перенесем начало координат в точке :
:
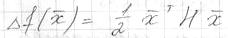 .
. - квадратичная форма. Поведение функции полностью определено знакоопределением Н.
- квадратичная форма. Поведение функции полностью определено знакоопределением Н.
Для произвольной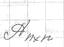 :
:
Угловыми главными минорами 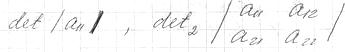 будем обозначать
будем обозначать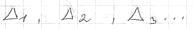 .Просто главные
.Просто главные
миноры (получаются при вычёркивании одноименной строки и столбца)
(получаются при вычёркивании одноименной строки и столбца)
Матрица Гёссе положительно определена только если все Матрица Н положительно полуопределена только если
где  - ранг Н, а Матрица Н отрицательно определена только если в ряду
- ранг Н, а Матрица Н отрицательно определена только если в ряду
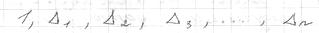 наблюдается строгое чередование знаков. Матрица Н отрицательно полуопределена только если в ряду
наблюдается строгое чередование знаков. Матрица Н отрицательно полуопределена только если в ряду
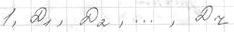 наблюдается наблюдается строгое чередование знаков,
наблюдается наблюдается строгое чередование знаков,
где 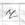 -ранг, а
-ранг, а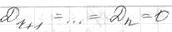
Матрица Н является неопределенной если в ряду нет строго чередования знаков, но отрицательные элементы присутствуют.
нет строго чередования знаков, но отрицательные элементы присутствуют.
9.Классическая задача условной оптимизации, метод неопределенных множителей Лагранжа(необходимые условия экстремума)
Задача условной оптимизации:

Метод неопределенных множителей Лагранжа
Необходимо 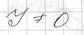 (якобиан). Точка
(якобиан). Точка 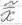 - полный дифференциал функции в этой точке = 0.
- полный дифференциал функции в этой точке = 0.
Эти дифференциалы связаны следующими зависимостями, которые получаются из (2), если разложить их в ряд Тейлора и ограничиться свободным членом I-го порядка.
Домножим любое выражение из (4) на неопределенный множитель |
и затем (3)+(4). |
Чтобы оптимальное решение находилось в точке 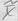 необходимо выполнение условия (5)
необходимо выполнение условия (5)
Система (6) имеет единственное решение в точке : |
.Это |
следует из того, что якобиан этих функций ограничений . К системе (6) мы должны добавить необходимое условие
. К системе (6) мы должны добавить необходимое условие
Для решения задачи (1)-(2) формируется функция Лагранжа:
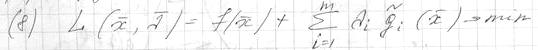 . Для всего набора (n+m) неизвестных выписывается условие стационарности:
. Для всего набора (n+m) неизвестных выписывается условие стационарности:
Решая (9)-(10) находим набор стационарных точек для исходных функций.
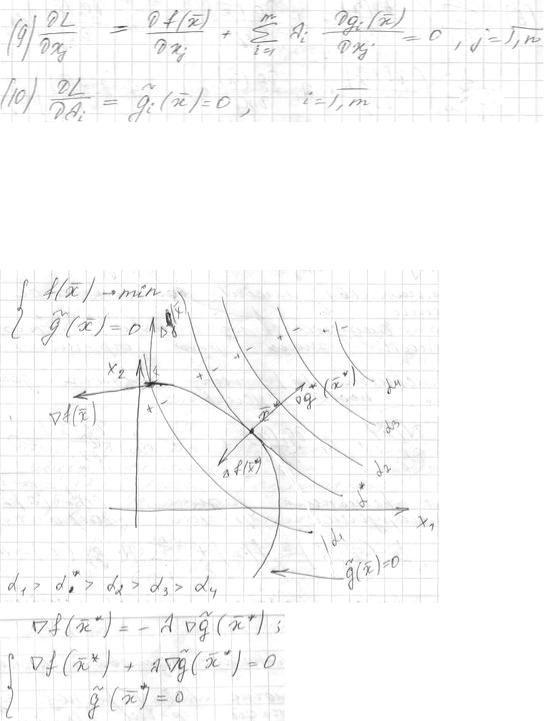
10.Геометрическая интерпретация множителей и метода Лагранжа, достаточные условия экстремума, седловые точки, решение задач с ограниченияминеравенствами классическим методом Лагранжа
Задача (8)(9)(10) дает возможность найти стационарные точки. Привлекаем аппарат вторых производных для анализа поведения функции в этих стационарных точках.
В любых
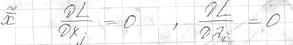 ,численно
,численно в каждой такой точке. Нас интересует изменение значения функции Лагранжа при
в каждой такой точке. Нас интересует изменение значения функции Лагранжа при
изменении  :
:

Точка  называется седловой точкой функции если для неё выполняется например такое соотношение:
называется седловой точкой функции если для неё выполняется например такое соотношение:
Стратегическая седловая точка функции Лагранжа 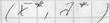 , если выполняется
, если выполняется
.

11. понятие о численных методах оптимизации
В любом численно методе так или иначе выбираются точки в пространстве которые являются последовательными приближениями к х* (решению задачи) В каждой точке выполняются определенные вычисления и получаются результаты y.
Алгоритм считается заданным если
1)задана последовательность точек вычисления
2)определены какие вычисления выполняются в каждой точке
3)задано условие остановки алгоритма
если метод при своей работе использует только значения функции цели и функций ограничений, то такой метод называют методом первого порядка. Если дополнительно используются значения n-ых производный то это метод n-го порядка.
Методы подразделяются на пассивный и последовательный поиск.
В методе пассивного поиска все точки задаются заранее до начала работы алгоритма. При последовательном поиске очередная точка определяется после того, как была определена предидущая.
Любой численный алгоритм задается простой формулой:
x(k +1) = x(k ) + ak h(k ), k = 0,1,2.. ak = const h(k ) - определяет направление шага, константак ak
определяет длину шага.
Численные методы подразделяются на конечношаговые и безконечношаговые. Конечношаговые – это методы линейного и квадратичного программирования, остальные безконеяношаговые. Важной характеристикой для безконечношаговых методов ябляется сходимость. Говорят что метод сходится если x(k ) - > x(*) pri k - > ¥ , часто говорят что
метод сходится по функции если f (x(k ) )® f (x *), k ® ¥ . Последовательность точек
x(0 ), x(1),..., x(k ) для которых f (x(0) )> f (x(1) )> ... >
называется минимизирующей (релаксирующей) последовательностью. Сходимость алгоритма часто оценивается с помощью скорости сходимости. Метод сходится линейно ( слинейной скоростью ) если для него можно подобрать q от (0,1) и некоторое число ko –
номер операции при котором выполняется: || x(k +1) - x* ||£ q || x(k ) - x* || pri k ³ k0
2) говорят что метод сходиься со сверхлинейной скоростью если для него выполняется
соотношение: || x(k +1) - x* ||£ qk +1 || x(k ) - x * pri qk +1 ® 0 + pri k ® ¥ .
3) с квадратичной скоростью если можно подобрать некоторое константу с>0 при которой выполняется соотношение|| x(k +1) - x* ||£ c || x(k ) - x* ||2 pri k ³ k0 .
Используются следующие условия остановки работы алгоритма:
1)|| x(k +1) - x(k ) ||£ ε1
2)|| f (x(k +1) )- f (x(k ) )||£ ε 2
3)|| f '(x(k +1) )||£ ε 3
Эти же условия остановки обычно записываются так:
1) |
|| x(k +1) - x(k ) ||£ ¶1 (1- || x(k +1) ||) |
|
2) |
|| |
f (x(k +1) )- f (x(k ) )||£ δ 2 (1- || f (x(k +1) )||) |
3) |
|| |
f '(x(k +1) )||£ δ3 (1+ || f '(x(k +1) )) |
Точка х* является локально устойчивой если к ней сходится любая минимизируящая последовательность.
