Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

mo-crib-03

.pdf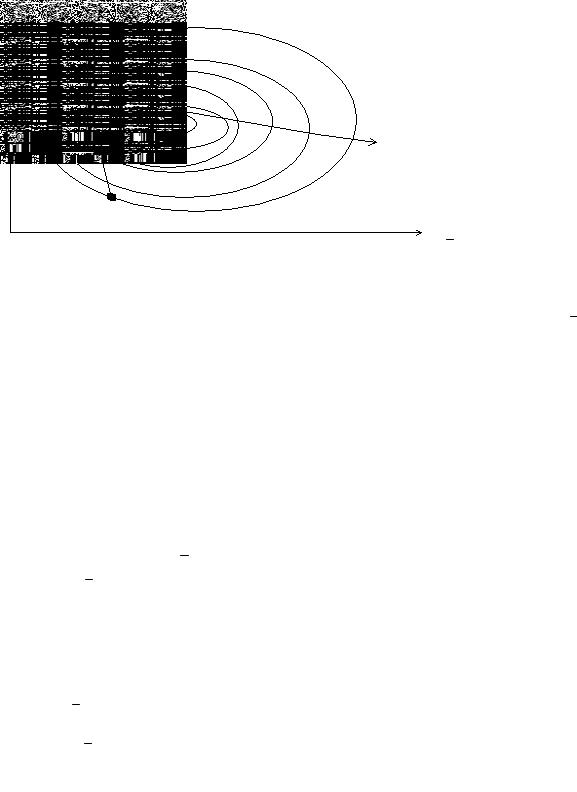

Скачиваний:

116

Добавлен:

09.02.2015

Размер:

11.29 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 144 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Вопрос 20.

Градиентные методы: с постоянным шагом, с дроблением шага.

Градиентный метод с постоянным шагом.

(k +1) =

( k ) −αf ′(

(k ) ), k = 0,1,2...

∂f (

)

x(jk +1) = x(jk ) −α

, j =

x(k )

1, n

∂x j

f (x) = ax2

x(k +1) = x( k ) − 2αax( k ) = x(k ) (1 − 2αa)

1)0 < α <

− метод

_ сходится

2)α >

− метод

_ расходится

3)α =

− зацикливан ие

Если выбирать малые α , метод надёжно приводит в точку x* . Иначе метод может заканчиваться неудачно.

Градиентный метод с дроблением шага.

В методе длина шага постепенно уменьшается по мере приближения к точке x* . На каждой итерации шаг выбирается таким образом, чтобы для него выполнялось соотношение:

f ′(

f (

(k ) −αk

(k )

)) − f (

(k ) ) ≤ −εαk

f (

(k ) )

14243

(k )

′

(k )

f (x) = f (x

) x

) + f (x

Выбирается шаг достаточной величины и проверяется выполнение соотношения. Если выполняется – делаем уменьшение. Если нет – дробим шаг, пока соотношение не начинает выполняться.

− f ′(x (1) )

− f ′(x (0) )

	(2)		(3)
x		x

	*	− f ′(		(2) )
x			x

x (1)

x (0)

x (k +1) = x (k ) − α k f ′(x (k ) ), k = 0,1,2...

Если f (x) такая, что для нее существует постоянная Липшица

(для которой:

f (

) − f (

)

≤ R

−

, x, y Ε n ), то α

= α = const =

1 − ε

Если для матрицы f ′′(x) вычислять оценки сверху и снизу для наибольшего и

наименьшего собственных чисел такой матрицы, то тогда α k = α − const = 2(1 − ε )

21. Метод наискорейшего спуска, метод покоординатного спуска, сходимость градиентных методов.

Метод Коши (наискорейшего спуска)

_ (k +1)	_ (k )	−α		_ ( k )
x	= x	−α	k	f \| (x ) ; k=0,1,2….
			k

α k выбирается оптимальной величиной, обеспечивающей достижение min функции при

_ (k )

движении в направлении f | (x

)

из точки x .

_ ( k )

_ (k )

= arg_ min_ f x

− αf | (x

)

;

α ³0

_ (k )

_ (k +1)

Направления

f | (x

) и

f | (x

)

взаимно ортогональные:

(α ) =

_ (k )

− αf ||

_ (k )

f (x

)) - направление ее min-ции;

dϕ

_ (k )

_ (k +1)

d x

= − f | x

| x

= 0

dα

d x

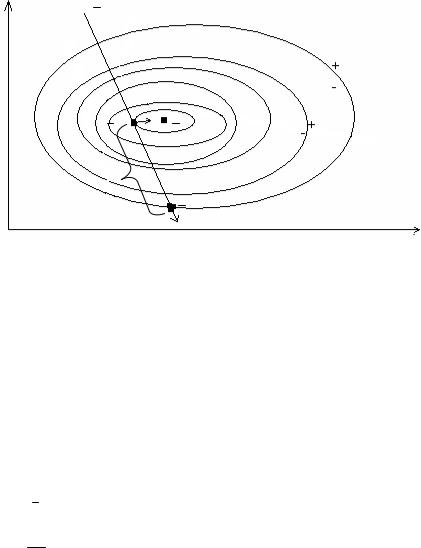
Геометрическая интерпретация: X2

− f ′(x (k ) )

x (1)

x *

α 0

x (0)

Градиентный метод покоординатного спуска. Движение вдоль какой-либо оси на каждом шаге.

						_ (0)
	(0)		(1)		(0)	∂f (x ) e1
x ; x = x − α 0						∂f (x ) e1
	_	_		_		_
						∂x1
						_ (1)
	_ (1)		(2)		(1)	_ (1)
	_ (1)	_	(2)	_	(1)	_
x ; x				= x	− α1	∂f (x ) e2
						∂x2

...
							_ (kn+s-1)
_ (kn+s -1)				_ ( kn+s ) _ ( kn+s-1)			∂f (x	_
x			; x		= x	− α kn+s-1	∂f (x	)	es
x			; x		= x	− α kn+s-1	∂xs		es
							∂xs

Где ei - столбец с нулями на всех местах кроме

k = 0,1,2....

k – число внешних итераций;

s = 1, n

- спуск по всем направлениям;

i-ого, на нем 1.

x(kn+s )		= x( kn+s-1)	; __ j =		1; n		; __ j ¹ s;
	j	j
									kn+s-1
									kn+s-1
x(kn+s )		= x( kn+s-1)	- α			¶f (x				)	; __ j = s;
x(kn+s )		= x( kn+s-1)	- α	kn+s -1				¶xs			; __ j = s;
	j	j		kn+s -1				¶xs

Если αkn+s-1 =const, то имеем постоянный шаг;

Если α выбирается оптимальной длинной, то имеем покоординатный спуск, называемый

методом Гаусса – Зейделя.

(kn+s -1)

α kn+s-1

= arg_ min_ f

(kn+s-1)

- α

¶f (x

)

;

¶xs

α ³0

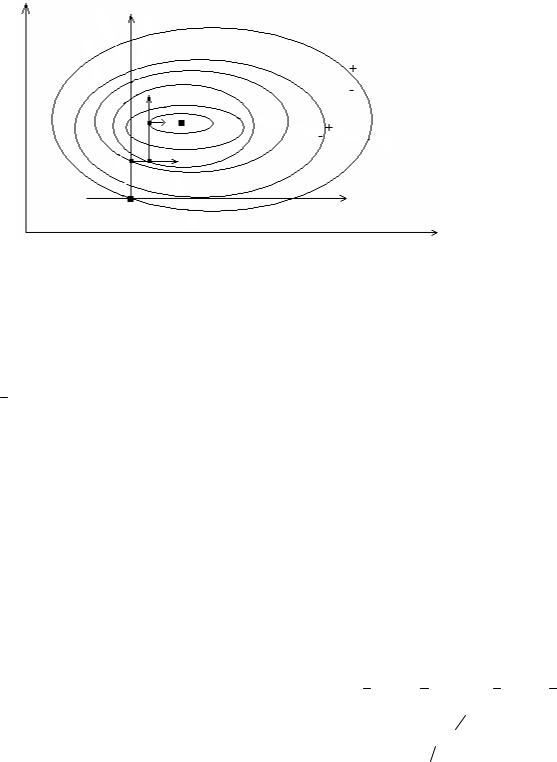
Геометрическая интерпретация: X2

					(3)				*
				x	(3)			x	*
		(1)					(2)
x		(1)				x	(2)
			(0)
	x		(0)

Теоремы о сходимости градиентных методов:

1. Если f(x) ограниченно снизу и ее градиент удовлетворяет условию Липшица, т.е.

выполняется соотношение: || f | (

) - f | (x) ||£ R ||

|| ,

Î E n ; y ¹ x;

(k +1) =

(k ) - α k

f | (

(k ) ) ; k=0,1,2…

. Где α k удовлетворяет соотношению из градиентного

метода с дроблением шага:

f (x

( k ) - α k f | (

(k ) ))- f (

(k ) ) £ -ξα k || f | (

(k ) ) ||2 ;α k > 0; __ 0 < ξ < 1;

То тогда справедливо, что ||

f | (

(k ) ) ||® 0, при _ k ® ¥, _ для _ "

(0) ;

( k )

Условие остановки:

¶f (x )

£ ξ ;

¶x

2. Если f(x) является непрерывно дважды деференцируемой функцией, для которой

||£

f | (

)

£ M ||

|| ; "

Î E n ; y ¹ x;

выполняется соотношение :

m || y

то она называется сильно выпуклой функцией. Тогда для процесса

(k +1) £

(k ) - α k f | (

(k ) ) ;

_ ( k )

_ (k )

(0)

выполняется соотношение:

α k = arg_ min_ f x

- αf | (x

)

, то для начальной точки x

α ³0

(k ) ®

(*) ; f (

(k ) ) ® f (

(*) ) .

f (x

( k ) )- f (x

* )£ g k (f (x

(0) )- f (x

* ))

Для скорости сходимости справедливы зависимости: || x(k ) - x*

||£ Cg 2

g = (M - m) (M + m); _ g Î [0;1]

C = const < ¥

M и m: равномерные по х оценки сверху и снизу, наибольшее и наименьшее собственные

числа матрицы f || (x) . В качестве приближения можно взять собственные числа f || (x ) .

22. Градиентный метод с масштабированием переменных.

(Для f вида f = ∑ α k x 2j , сепарабельных функций)

j =1

В случае когда g<<1 задача является хорошо обусловленной и решается достаточно быстро. А если M и m сильно отличаются друг от друга и g≈1, то задача является плохо обусловленной и требует большого числа итераций.

На примере:

(0)

f (x) = x 2

+ 16x 2 → min

H =

= α − 12 y

= α 12 x

; j =

= μ

; x

1, n

;

f (

) = y 2

+ y 2

→ min

тогда выполняют замену переменных:

μ j = α −j 12

(0)

| (x) =

f | (x )

f | ( y

) =

32x2

Для более сложных функций, компоненты μ j

пересчитываются на каждом шаге , по

∂

− 12

f (x )

формуле μ

= 1, n , где

точка одномерного min-ма функции, при

∂xi ∂xi

(k )

в направлении переменной xi .

движении из x

(k +1)

(k )

− α

(k )

μ 2

1 0

= x

f | (x )

B =

μ2

0 16

23. Эвристические схемы градиентных методов.

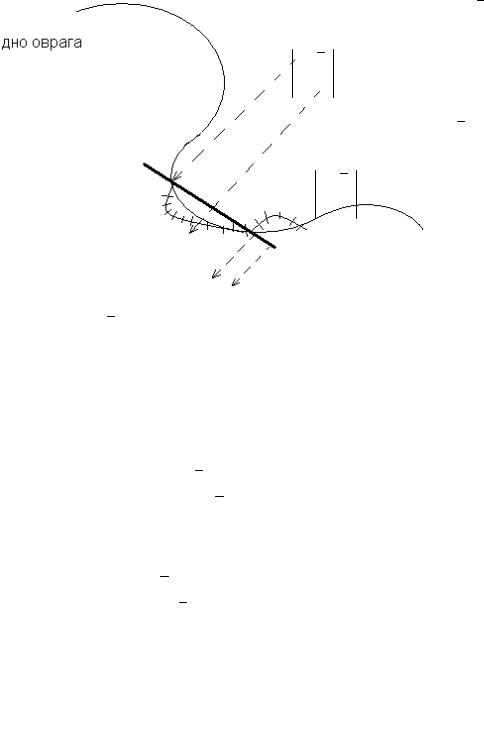
Эвристический метод с переключающимся алгоритмом.

Применяется для функций со сложной топографий линий уровня. Состоит из 2 процедур:

1. Принимаем некоторое ξ1 << 1 и затем принудительно полагаем ¶f (x) = 0 , x j такие, что

¶x j

действительно выполняется соотношение ¶f (x) £ ξ1 . Движение осуществляется ко дну

¶x j

оврага, в сторону сильно уменьшающихся значений функции.

2. Устанавливаем некоторое ξ2 >> 1, принудительно полагаем ¶f (x) = 0 , для которых в

¶x j

действительности выполняется соотношение ¶f (x) ³ ξ2 , в результате будим двигаться в

¶x j

направлении вдоль оврагов. На практике такие процедуры чередуют.

Метод Гельфанда ( обладает линейной скоростью сходимостью)

(01)

(02)

(1,1)

(2,2)

24. Оптимизация многомерных функций методами второго порядка.

В методах второго порядка производиться квадратичная аппроксимация. Практически за один шаг обрабатывают любую квадратичную функцию. Для более сложных больше.

Метод Ньютона:

_ (k +1)	_	(k )	_ (k )	_ (k )
x	= x		− ( f \|\| (x ))−1 f \| (x )

Квадратичная скорость сходимости.

Метод Ньютона – Фафстона ( модифицированный метод Ньютона с регулированием шага)

_ ( k +1)	_ (k )		_ (k ) −1			_ ( k )
		\|\|			\|
x	= x − α k f	\|\|	(x )	f	\|	(x ) ;
x	= x − α k f		(x )	f		(x ) ;

α				_ (k )		_ (k )		_ (k )
α	k	= arg_ min_ f x			− α f \|\| (x		)	−1 f \| (x )	;
	k								;


		_ (k +1)	) ≤	_ (k )
f (x			) ≤	f (x ) ;

Релаксационная последовательность.

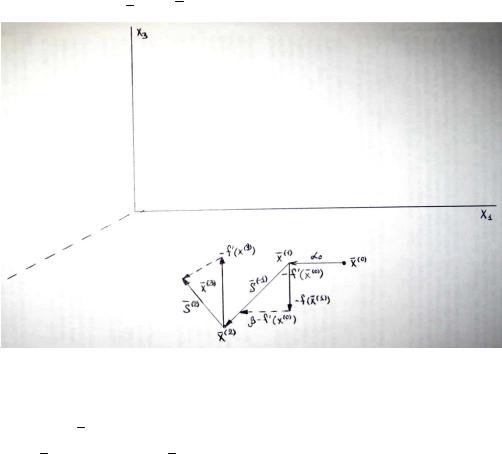
25. Метод сопряженных градиентов.

Метод Флетчера-Ривса

(k +1) =

(k ) + α

(k ) , k = 0,1,2...

(0) = − f ′(

(0) )

( k ) = − f ′(

(k ) ) + β

( k -1)

? k = 1,2,...

k -1

Направления S были взаимносопряженными.

( k ) ,

(k -1) ; f (

) = a + (

) +

(

) → min

, Hx

(

(k -1) ) = 0; = −( f ′(

(k -1) ) + β

(k ) ; HS

(k ) ), HS

(S (k -1)

, HS (k -1) );

k -1

= ( f ′(

( k -1) )

(k ) , HS

k -1

(S (k -1) , HS (k

-1) )

Длину шага выбирают оптимальной и для любой квадратичной функции:

′

(

(k ) ,

(k ) )

;

(S (k ) , HS ( k ) )

Для более сложных функций: α k = arg minα ³0 f (x (k ) + αS (k ) );

( k -1) , f ′(k ) , β

k -1

(k +1) =

( k ) + α k

(k ) H

(k +1) = Hx

(k ) + α k HS

( k )

+ Hx

(k +1)

+ Hx

(k )

+ α

(k )

14243

f ¢(

( k +1) )

( k )

f ¢( x

)® f ( x )=a+( x ,b )+

( x ,Hx )

(k ) = f (

(k +1) ) − f (

(k ) ),

( k -1)

= f ′(

( k ) ) − f ′(

(k -1) ),

-1

= ( f ′(

(k -1) ) = ( f ′(

( k ) ), f ′(

(k ) ) − ( f ′(

(k ) ), f ′(

(k -1) )) =

( k ) ), HS

-1

(S (k -1) , HS ( k -1) )

(S (k -1) , f (x (k ) ) − (S (k -1) , f ′(x (k -1) ))

( f ′(

(k ) ), f ′(

(k ) ))

( f ′(

(k ) ), f ′(

(k ) ))

− (− f ′(

(k -1) ), f ′(

(k -1) ) − β

(

(k -1)

( k -2) )

( f ′(

(k -1) ), f ′(

(k -1) ))

k -2

Алгоритм:

1.Задаем x (0) , S (0) = − f ′(x (0) )

2.k-ый шаг. Попадаем первый раз с параметрами . Вычисляем оптимальную длину шага. α k = arg min λ ³0 f (x (k ) + αS (k ) );

x (k +1) = x (k ) + α k S (k )

3.Осуществляем проверку. Вычисляем:

f (x (k +1) )

f ′(x (k +1) )

Проводим проверку на остановку алгоритма. Если || f ′(x (k +1) ) ||≤ ε → останавливаем алгоритм.

x (k +1) − приближение_ к _ x *

4.Вычисляем коэффициент

		=	( f ′(		( k +1) ), f ′(		(k +1) ))
β			( f ′(	x	( k +1) ), f ′(	x	(k +1) ))
β	k
	k		( f ′( x (k ) ), f ′( x (k ) ))
			( f ′( x (k ) ), f ′( x (k ) ))

Вычисляем S ( k +1) = − f ′(x (k +1) ) + β k S (k ) и переходим к п.2 алгоритма.

Для любой квадратичной функции дает гарантированное решение за n шагов(суперлинейная сходимость). Алгоритм первого порядка, т.к. нет вторых производных.

Для более сложных функций после каждой n итерации работу алгоритма нужно повторять в кол-ве x (0) для нового повторения брать последнюю точку из пред. работы алгоритма.

<<< < Предыдущая 1 2 34 / 144 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
06.09.201999.78 Кб19Ministerstvo_obrazovania_i_nauki_Rossyskoy_Fed....docx
#
09.02.20151.32 Mб107MIPI_DSI_Specification_v1b_8320061508.pdf
#
09.02.20153.63 Mб9MM2 TP.pdf
#
09.02.20158.01 Mб338MNE_Физика и технология микро- и наносистем.pdf
#
09.02.20154.31 Mб9MNG.pdf
#
09.02.201511.29 Mб116mo-crib-03.pdf
#
09.02.2015173.57 Кб8MO_laba_4.doc
#
20.09.20192.79 Mб11mss-crib2.doc
#
09.02.20151.6 Mб7mss-crib2.pdf
#
21.09.20191.05 Mб14mss_answers.doc
#
18.08.2019261.63 Кб0MST 42-51.doc