
mo-crib-03
.pdf
Количественной характеристикой качества решаемой задачи является число
sup || x − x* ||2 |
|
|
|
|
обусловленности: μ = lim x Lδ |
|
2 |
|
где Lδ ={x | f (x)− f (x*) = δ , |
|
inf || x − x* || |
|
|
|
δ→0 |
|
|
|
|
|
x Lδ |
|
|
|
понятно что μ >=1 если μ примерно равно 1 то говорят что задача хорошо обусловлена, т.е ее линии уровня представляют собой концентрические окружности. Если μ >>1 то линии уровня сильно вытянулы в одних направлениях и слабо в других.
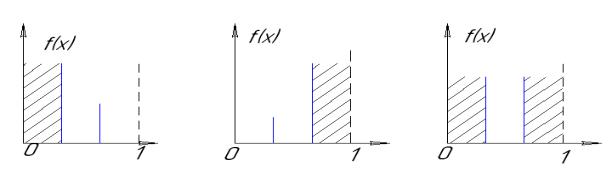
12. одномерный пассивный поиск.
Унимодальные функции(имеющие единственный минимум на заданном интервале). Вычисление значения функции в точке называется эксперимент. По результатам любой пары экспериментов на исходном интервале можно сузить исходный интервал и возможны 3 исхода:
Эффективность поиска определяется стратегией расположения экспериментов. Интервалом неопределенности называетмя интервал возможных значений х в которых с гарантией находится точка минимума функции.
Пусть для f(x) выполнено N экспериментов х1,х2,…,xn олгда длинна интервала
неопределнности рассчитывается: 1) xk : f (xk ) = min f (xi ) 2) l(x1, x2,..., xn, k ) = xk +1
1≤i≤n
Пессимистическая оценка длинны интервала неопределнности:
Ln = L(x1, x2,..., xn) = max l(x1, x2...., xn, k )
Принцип выбора оптимальной стратегии (принцип минимакса) в качестве оптимальной надо выбирать стратегию, приводит к минимуму значению максимальной длинны интервала неопределнности т.е к минимуму значения пессимистической оценки длинны интрвала неопределенности. Ln -оптимальная стратегия
поиска. Ln |
) |
) |
inf max l(x1,...., xn, k ) эта стратегия не |
= L(x1,..., xn) = inf L(x1,..., xn) = |
|||
|
|
0≤x1...≤xn≤1 |
0≤x1...≤xn≤1 1≤k ≤n |
может дать результата хуже чем Ln , а скорее всего даст лучше
1) n-четное число экспериментов тогда
) |
= |
1 + ε |
) |
|||
Ln |
|
|
|
; __ xk |
||
n |
+ 1 |
|||||
|
|
|
||||
|
|
2 |
|
|||
|
|
|
|
|
||
|
(1 + ε ) |
k + 1 |
|
|
||
|
|
|
||||
|
|
|
|
|
|
|
= |
|
|
2 |
|
− |
|
|
n |
+ 1 |
|
|||
|
|
|
|
|||
|
2 |
|
|
|||
|
|
|
|
|
||
ε{ |
k + 1 |
|
− |
k |
} где […] – выделение целой части а ε - |
|
|
|
|
||||
|
2 |
|
|
|
||
|
|
|
2 |
|
||
минимально возможно расстояние на котором еще различимы f(x1) И f(x2) 2) (n+1) – нечетное число экспериментов
L |
= |
|
1 |
; L − L |
= 1 + ε |
− |
1 |
= |
|
ε |
|||||||
) |
|
|
|
|
) |
) |
|
|
|
|
|
|
|
|
|
|
|
n+1 |
|
|
|
n |
n+1 |
|
|
|
|
|
|
|
|
||||
|
n |
|
|
|
n |
|
|
n |
|
||||||||
|
|
|
+ 1 |
|
|
|
|
n |
+ 1 |
|
+ 1 |
|
+ 1 |
||||
|
|
|
2 |
|
|
2 |
|
2 |
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13. метод дихотомии метод свена
) |
− |
n |
|
− 2 |
− |
n |
|
Эксперименты проводим парами, L |
= 2 2 |
+ ε 1 |
2 |
|
|||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) метод свена (медод грубого поиска или метод удвоения интервалов) предназначен для первоначального сужения исходного интервала перед применением более сложных методов поиска.
) |
) |
+ x * 2k ; k = 0,1,2 |
xk +1 |
= xk |
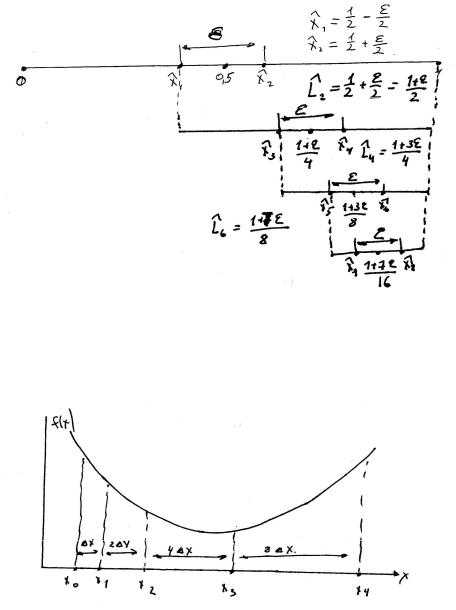
14. метод Фибоначчи метод золотого сечения.
1)метод Фибоначчи: в этом методе на первой итерации проводится 2 эксперимента а на каждой последующей итерации добавляется 1 эксперимент, причем эксперименты располагаются симметрично на расстоянии <0.5 Ltek на последней итерации два последних
эксперимента располагаются на расстоянии ε . Заранее рассчитывается n исходя из точности ε
Lk −1 = Lk + Lk +1 или L j−1 = L j |
+ Lj+1; j = |
__________ |
|
|||||||
2, n |
−1 |
|
||||||||
Расчитаем длины интервалов от конца : |
k = 1,..., n − 1 |
|||||||||
Ln = Ln |
|
|
|
|
|
|
||||
|
|
|
|
|
|
F |
− числа фиббоначи |
|||
Ln−1 = 2Ln |
− ε |
|
|
|
|
|||||
|
|
|
|
F0 |
= F1 = 1 |
|||||
Ln−2 = Ln−1 |
+ Ln = 3Ln − ε |
|
|
|
|
|||||
|
|
|
|
Fk |
= Fk −2 + Fk −1 |
|||||
Ln−3 = Ln−2 + Ln−1 = 5Ln − 2ε |
|
|
|
|
||||||
Ln−4 = Ln−3 + Ln−2 = 8Ln − 3ε |
|
|
|
|
|
|
||||
Ln−k = Fk +1 Ln − Fk −1ε |
|
|
< |
b0 − a0 |
≤ F |
|||||
|
1 |
|
Fn−2 |
n находим из F |
|
|||||
|
|
|
|
|||||||
Ln = |
+ |
ε |
n+1 |
|
|
ε |
n+2 |
|||
|
|
|
|
|
|
|
||||
|
Fn |
Fn |
|
|
|
|
|
|
||
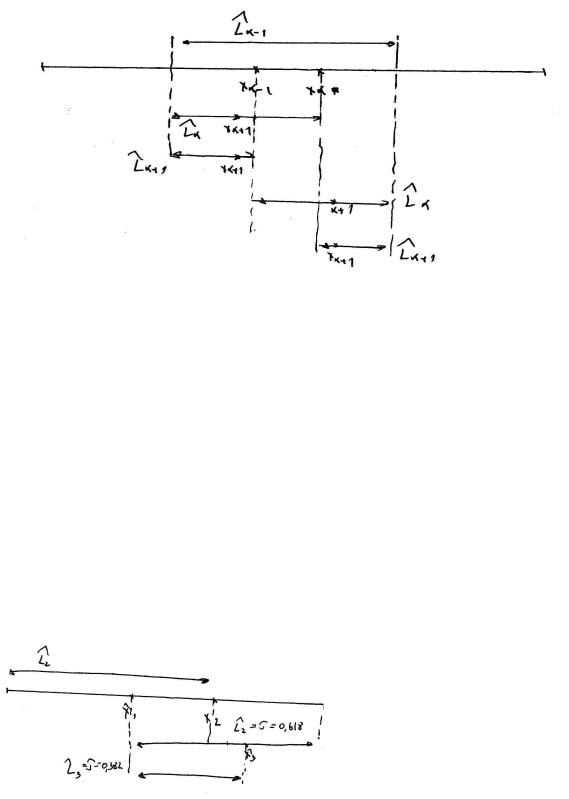
2) метод золотого сечения.
n-заранее не определяется L j−1 = L j + L j+1 - единственное начальное условие
Lj−1 |
= |
L j |
+ |
Lj+1 |
<=> 1 = τ + τ 2 => τ = 0.618 τ 2 = 1 − τ = 0.382 |
|
Lj−1 |
Lj−1 |
Lj−1 |
||||
|
|
L = τ n−1 |
||||
|
|
|
|
|
||
|
|
|
|
|
n |
Метод Фибоначчи и метод золотого сечения обладают линейной скоростью сходимости.
15. методы оценивания с помощью квадратичной аппроксимации.
1)метод однократного оценивания: f(x)- унимодальная непрерывная достаточно гладкая, тогда ее в ограниченном интервале можно аппроксимировать некоторой квадратичной функций а затем искать минимум этой квадратичной функции.
Есть 3 точки: x1, x2, x3 соответственно f1, f2, f3 потребуем чтобы в этих точках значение
ϕ(x) совпадало с f(x)
ϕ(x) = a0 + a1 (x − x1 )+ a2 (x − x1 )(x − x2 )
(x1 ) = ϕ(x1 ) = f 1 = a0 ; a0 = f1f
f (x2 ) = ϕ(x2 ) = |
f 2 = f 1 + a1 (x − x1 ); a1 = |
f2 − f1 |
|
|
|
|
|
|
||||||||||||||||||||||||
x2 − x1 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f2 − f1 |
|
|
|
|
|
|
|
|
|
|||||||
f (x ) = ϕ(x ) = f |
3 |
= f 1 + |
(x − x ) + a2 * (x − x )(x − x |
2 |
) => |
|||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
3 |
|
|
3 |
|
|
|
|
|
|
|
|
x2 − x1 |
|
3 |
1 |
|
|
|
3 |
1 |
3 |
|
||||||||||
|
|
|
|
|
|
|
|
− f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
=> a2 |
= |
|
|
|
|
f3 |
|
|
|
|
− |
|
|
|
f2 − f1 |
|
|
|
|
|
|
|
|
|||||||||
(x3 |
− x1 )(x3 − x2 ) |
(x2 − x1 )(x3 |
− x2 ) |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
ϕ '(x) = |
dϕ(x) |
= a + a |
|
(x − x |
|
) + a |
|
(x − x ) = 0 => |
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
2 |
2 |
|
|
|
|
|
||||||||||||||||||||||
|
a1 dx |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
~ |
|
(x2 |
+ x1 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x = − |
|
|
|
+ |
|
|
|
|
|
|
|
≈ x * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2a2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2)метод последовательного оценивания (метод пауэла): |
|
|
||||||||||||||||||||||||||||||
а) Предварительный. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Выбираем начальную точку х1 и шаг поиска |
x , рассчитываем f(x1) если |
|||||||||||||||||||||||||||||||
f (x2 = x1 + |
|
x) < f (x1 ), То x3 |
= x2 + |
x иначе x3 |
= x1 − |
x |
|
|
||||||||||||||||||||||||
б) переназначаем х1 х2 х3 в естественном порядке и (если надо заного вычисляем f1 f2 f3). Далее выбираем min f = min{ f1 , f2 , f3} и соответствующий xmin = arg(min f ) затем по методу однократного оценивания проводим квадратичную аппроксимацию х1 х2 х3 и
находим очередную точку приближения |
~ |
|
|
|
x |
|
|
||
~ |
~ |
то заканчиваем работы и |
|
|
проверяем если | min f − f (x ) ≤ ε1 И | xmin |
− x |≤ ε 2 |
|
||
~ |
|
|
|
|
xmin или x будут решением, иначе переходим в шаг в) |
|
|||
~ |
|
|
|
|
в) выбираем наилучшую из xmin или x и 2 точки по обе стороны от нее(из числа |
|
|||
имеющихся) и уходим на шаг б). |
|
~ |
|
|
замечание: на первой итерации алгоритма точка |
или |
|||
x может оказаться далеко за х3 |
||||
далеко перд х1 и тогда ее невозможно окружить 2-мя точками, тогда надо применить
метод свена и используя |
x провести несколько шагов из |
~ |
x , затем снова на шаг б) |
методы квадратичной аппроксимации обладают суперлинейной скоростью сходимости.
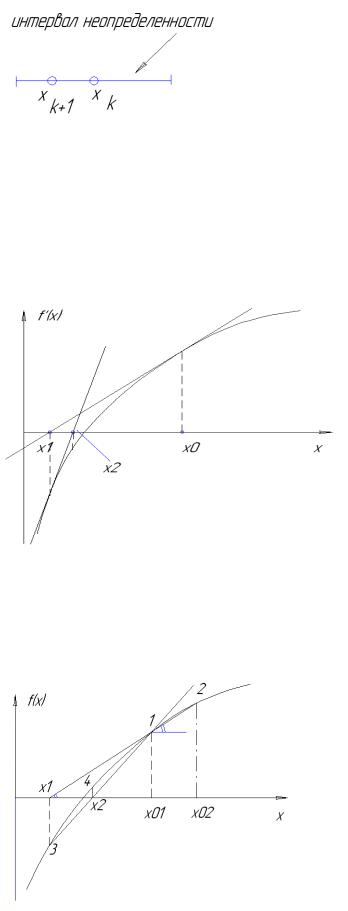
16) метод средней точки метод касательных метод секущих 1) метод деления интервала пополам ( метод средней точки):
по знаку f '(xk ) определяем неперспективную половину,
в оставшейся находим середину и вычисляем f '(xk +1 ) . Условие остановки: | f '(xk )|£ ε
2) метод касательных (метод Ньютона): Решение гарантировано если f(x) строго выпукла
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
f '(x), x . |
|
( f ''(x) > 0 ); f '(x) = 0 => находим x , работа происходит в координатной системе |
|
|||||||||||||||||
Выберем х0 и выполним начальную аппроксимацию т.е. разложим f '(x) в ряд Тейлора: |
|
|||||||||||||||||
0 = f '(x) = f '(x0 )+ f ''(x0 )(x - x0 ) |
|
|
|
f '(xk −1 ) |
|
|
|
|
||||||||||
~ |
f '(x0 ) |
~ |
|
f '(x1 ) |
|
~ |
|
|
|
|
|
|
||||||
x1 = x0 - |
|
|
; x2 = x1 - |
|
|
|
; xk |
= x1−1 |
- |
|
|
|
|
|
|
|
|
|
f ''(x0 ) |
|
f ''(x1 ) |
f ''(xk −1 ) |
|
|
|
|
|||||||||||
|
~ |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Условие остановки: | f '(xk )|£ ε |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Геометрическая интерпретация: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Если аналитического выражения для |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
производной не существует тогда |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
пользуемся разностными |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
выражениями: |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
) |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
f '(x) @ f '(x) = |
( f |
(x + g )- f (x - g )), |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2g |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
где g- даза оценки |
f (x + 2g ) - 2 f (x)+ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
f ''(x) @ f ''(x) = |
|
|
|
2g ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4g |
+ f (x - |
|
||
3) метод секущих: более универсальны (не надо искать 2 производную) работает в том числе и на невыпуклых функциях, но для гарантии решения требует чтобы для
невыпуклых функций знаки производных были различны в очередных 2-х точках f '(x1 )× f '(x2 ) < 0
Запишем уравнение для секущей:
0 = f '(x) = |
(x − x0 )( f '(x02 ) − f '(x01 )) |
+ f '(x ), |
||||
|
|
|||||
|
|
(x02 - x01 ) |
01 |
|||
|
|
|
|
|||
находим x = x - |
f '(x01 )(x02 − x01 ) |
|
проводим |
|||
f '(x02 ) - f '(x01 ) |
||||||
|
01 |
|
|
|||
|
|
|
|
|||
очередную секущую через точки 3 и 1 если f '(x2 ) > 0 то очередную хорду проводим через 3 и 4.
условие остановки: | f '(xk )|< ε

17) метод поиска по симплексу( S 2 метод ) 1962 год , Нелдер и Мид 1965.
Симплекс – это многогранник в n-мерном пространстве, образованный n+1 вершинами, стоящих на равном расстоянии друг от друга.
Процедура отражения любой вершины симплекса, т.е перенос некоторой вершины симплекса по прямой, проходящей через эту точку и через центр тяжести остальных вершин на некоторое расстояние(т.е используя свойство симплекса что на любой его гране можно построить новый симплекс. xn1-нормальное отражение, xn2-растяжение симплекса Применительно к k-ой итерации
1) если надо, переобозначаем вершины x(0 ) (k ), x(1) (k ),..., x(n ) (k )так чтобы оно
удовлетворяло
f (x(0) (k ))≤ f (x(1) (k ))≤ ... ≤ f (x(n ) (k )), при этом n-
ая точка является худшей точкой и отражению подвергается всегда худшая точка.
2) Найдем центр тяжести остальных вершин
1 n−1
x(c ) (k ) = ∑ x(i ) (k ) n i=0
3)Вычислим пробную точку для нормального отображения u (k ) = x (n ) (k )+ (1 + Q)(x (c ) (k ) − x (n ) (k )), Q = α = 1
Случай α : f (x (0 ) (k ))≤ f (u (k )) ≤ f (x (n−1) (k ))=> именно u (k ) вершиной заменяем x (n ) (k ) и уходим на (k+1) итерацию
Случай β : если f (u (k )) < f (x(0) (k )) то направление перемещения в u (k ) перспективно
итогда следует проверить случай растяжения симплекса в этом направлении
v(k ) = x (n ) (k ) + (1 + Q )(x (c ) (k ) − x (n ) (k )), Q = β = 2 если f (v (k )) < f (u (k )) то u (k )
удаляем и заменяем ее на |
|
(k ) |
иначе заменяем |
|
|
|
(n ) (k ) на |
|
|
|
(k ) и уходим на начало |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
v |
x |
u |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(к+1) итерации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Случай γ :если f ( |
|
(k )) > f ( |
|
|
|
(n−1) (k )) |
|
вычисляем пробную |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
u |
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если f ( |
|
(k )) ≤ f ( |
|
|
|
(n ) (k ))то |
|
(n ) (k )+ (1 + γ )( |
|
(c ) (k )− |
|
(n ) (k )) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
x |
x |
x |
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
величину |
|
|
|
|
(k ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n ) (k )+ (1 − γ )( |
|
|
|
|
|
|
|
|
|
|
|
(n ) (k )) |
|
γ = 0.5 |
|
|
|||||||||||||||||||||||||||||||||||||||||
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c ) (k ) − |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иначе |
x |
x |
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Если f ( |
|
|
(k )) < min{ f ( |
|
|
(k )), f ( |
|
|
(n ) (k ))} то поиск удачен и вершиной |
|
|
|
(k ) заменяем |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
w |
u |
x |
w |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вершину |
|
(n ) (k ) и уходим на начало (к+1) итерации, иначе равномерно сжимаем |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_____ |
|
|
симплекс к вершине |
|
|
(0) (k ) по формуле |
|
(i ) (k ) = |
|
(i ) (k ) |
+ 0.5( |
|
|
(0) (k ) − |
|
(i ) (k )) i = 1, n и |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
x |
x |
x |
x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
уходим в начало (к+1) итерации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие остановки: |
1 |
∑n |
[f ( |
|
|
|
(0) (k + 1))− f ( |
|
(i ) (k + 1))]2 |
|
≤ ε |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Процедура построения начального симплекса: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(0) (0) = (x , x |
|
,.., x |
|
|
)T , тогда |
|
|
(1) (0) = (x |
+ r, x |
|
|
+ s,..., x |
|
|
+ s); |
|
(2 ) (0) = (x |
+ s, x |
|
+ r,..., x |
|
+ s); |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
2 |
n |
x |
2 |
n |
|
x |
2 |
n |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
(n ) (0) = (x |
+ s, x |
|
|
|
+ s,..., x |
|
|
+ r); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x |
2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 1 |
+ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если μ = 1 то ребра |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n + 1 − 1 |
|
|
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
где r = μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; s = μ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
начального |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
симплекса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеют примерно |
|
|
||||||||||||||||||||||||||||||||||||||

единичную длину.
Если некоторая вершина не исключается к М-ой итерации то текущий симплекс заменяется новым с вершиной x (0) , соответсвующей наилучшей в текущем симплексе.
M =1.65n + 0.05n2

18) метод поиска Ху-ка Дживса.
Если из x (k ) выходить и двигаться в направлении d = (x (k ) сходиться быстрее к точке x *.
Первая процедура: исследующий поиск. x (t ) - текущая точка (базовая) выбираются
x |
; j = 1, n пробные шаги затем из |
|
(t ) |
делаются 2 шага ± |
x и фиксируются и |
x |
|||||
j |
|
|
|
|
1 |
фиксируются значения остальных координат, если один из них привел к успеху т.е уменьшению функции, то фиксируемся в этой точке и уже из нее делаем шаги вдоль следующей координаты ± x2 в результате находиться точка x(t+1) . Эта процедура обеспечивает локальный поиск и движению к дну оырагов.
Вторая процедура: поизк по образцу x (k +1) = x(k ) + (x (k ) − x (k −1) ), x(k ) и x(k −1) - базовые точки, производиться движение вдоль оврагов.
Алгоритм:
Подготовительный этап: 1. x (0) , x j j = 1, n,α > 1 ε > 0
Шаг 2: в последней из найденных базовой точке x (k −1) производим исследующий поиск (в начале это точка x (0) ), если он приводит к успеху то последнюю из успешно найденных точек обозначаем x (k ) и переходим к 4.
Шаг 3: если || x ||≤ ε то остановка последняя из базовых точек является
окончательным приближением, иначе уменьшаем шаг x j = |
x j |
; j = 1, n |
|
α |
|||
|
|
Шаг 4: выполняем поиск по образцу x (k +1)врем1 = x (k ) + (x (k ) − x (k −1) ) затем проводим в найденной точке исследующий поиск и получаем xврем(k +1)2 и выбираем наилучшую
)], если f (x(k +1) )< f (x)(k ) , то шаг 4 считаем удачным и
уходим на его начало, при этом проводим переобозначение
точек x(k +1) − > x(k ); x(k ) − > x(k −1) , иначе остаемся в последней базовой точке x(k ) н
обозначаем ее как x(k −1) и уходим на шаг 3.
19. метод сопряженных направлений Пауэла.
Предназначен для минимизации функций: f (x) = a + bx + 0.5xT Cx- > min не боее чем за n итераций (работает в рациональных дробях)
На первых (n-1) итерациях находится совокупность направлений в пространстве
d (1) , d (2 ),..., d (n−1) и на n-ой итерации выполняется последующая минимизация в этих направлениях. Фактически переходим в новую систему координат, оси которой совпадают с осями квадратичной функции Cn×n является диагональной,
d (i ) и d ( j ) называются сопряженными или сопряженными по отношению к матрице С,
или С-ортогональными, если выполняется: d (i ) T · C · d ( j ) = 0 i, j = 1, n i ¹ j
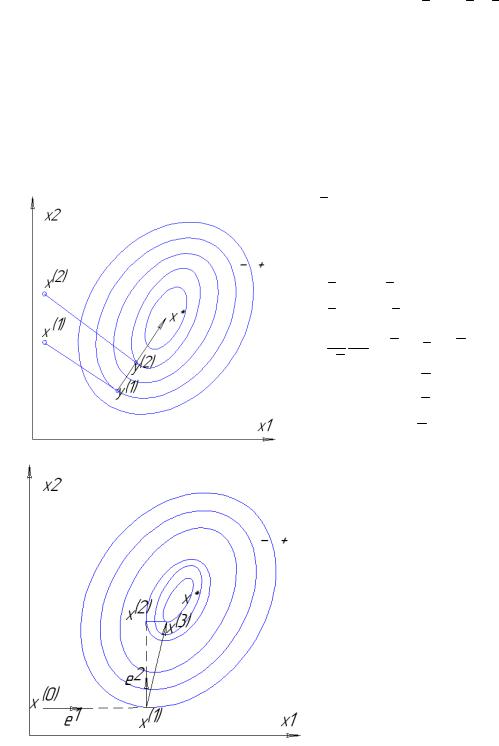
Работает для любых направлений. Докажем что (y(2) - y(1) ) является сопряженным с d
Это свойство для квадратичной функции называется построением параллельног оподпространства.
x (1), d , f (x (1) + λd ), y(1)
(21) ( (2) + λ ) (2 )
x , d , f x d , y
df dx = (b T + x T C )d = 0 dx dλ
(bT + y(2 ) T C )d = 0 - (bT + y(1) T C )d = 0
= (y(2) - y(1) )Cd = 0
Обычно выходят из одной начальной точки Алгоритм:
1. задаем начальную точку x(0) и набор линейно независимых ортогональных направлений S (1) , S (2 ),..., S (n )
2. строим текущюю линейку направлений поиска(в начале S (1) , S (2 ),..., S (n ) ), затем из последней точки эксперимента делаем (n+1) последовательных шагов минимизации функции в направлениях S (n ), S (1), S (2 ),..., S (n ) и обозначаем точки
минимизации x(1), x(2),.., x(n+1) 3. определяем новое сопряженное
направление d (1) = x(n+1) - x(1)
4.формируем очередную линейку направления поиска S (1) , S (2 ),..., S (n ) и в конец дописываем очередное сопряженное направление и выбрасываем
первое S (2),..., S (n ) , d (1) и уходим на шаг 2
со 2-ой итерации выполняем (n+1) шагов последовательного поиска в направлениях d (1) , S (2),..., S (n ), d (1) в результате находим d (2) ,сопряженное с d (1) , после (n-1) итерации алгоритма получаем S (n ) , d (1) , d (2) ,..., d (n−1) , и теперь рассмотрим n задач последовательной минимизации, в результате получим решение задачи.
Сходимость – суперлинейная.
