Лекции_ЭиМ

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Следовательно,

.pdf

Скачиваний:

Добавлен:

09.02.2015

Размер:

1.22 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Электричество и магнетизм

Электростатика

Между заряженными и намагниченными телами действуют силы, называемые электромагнитными. Природа электромагнитных сил обусловлена электрически заряженными частицами, входящими в состав всех тел материального мира. Опытным путем установлено, что электрические заряды обладают следующими свойствами.

◦Заряды бывают двух видов: положительные и отрицательные. Одноименные заряды отталкиваются, разноименные – притягиваются.

◦Алгебраическая сумма зарядов изолированной системы постоянна.

◦Электрический заряд является релятивистским инвариантом.

◦Наименьшим по абсолютной величине элементарным зарядом, равным 1,6·10-19 кулона (Кл) является отрицательный заряд электрона или равный ему по модулю положительный заряд протона.

Закон Кулона: силы, с которыми два неподвижных точечных заряда Q и q действуют друг на друга в вакууме, пропорциональны произведению их величин и обратно

пропорциональны квадрату расстояния между ними

	Qq				,
F				er
	4	o	r 2

где							- единичный вектор в направлении
где	o	= 8,85·10-12 Ф/м– электрическая постоянная; e					- единичный вектор в направлении
	o					r
			Q		q
			Q					F	F
								F	F	-
		F				F				-
			er	r

Одноименные заряды	Разноименные заряды

(1)

r (рис.1).

Рис.

Заряды порождают в окружающем пространстве электрическое поле, проявляющееся в том, что помещенный в любую точку пробный заряд испытывает действие силы. Поле характеризуется векторной величиной, называемой напряженностью.

Напряженностью электрического поля называется отношение силы, действующей на

электрический заряд q, к величине этого заряда
	F
E		.	(2)
E	q	.	(2)
	q

Направление вектора E совпадает с направлением силы, действующей на положительный пробный заряд. Подставляя (2) (1), получим выражение для напряженности поля точечного заряда Q:

	Q
E				er .	(3)
E	4	o	r 2	er .	(3)
		o

Это выражение называют законом Кулона в полевой форме. Размерность напряженности в СИ: [E]=[В/м] - вольт на метр; =[Н/Кл] - ньютон на кулон,– здесь и далее в квадратных скобках мы будем обозначать ра змерности величин. По известной напряженности в любой точке поля легко найти силу, действующую на точечный заряд q, помещенный в эту точку поля:


F	Eq .	(4)

Принцип суперпозиции: сила, с которой система из n зарядов, действует на заряд, не включенный в эту систему, равна векторной сумме сил, с которыми действует каждый заряд системы на данный:


F	F1	F2	F3	... Fn .	(5)

Отсюда следует и аналогичное выражение и для напряженностей:


E E1		E2	... En .	(6)

Напряженность поля системы точечных зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности.

Электростатические поля изображают графически с помощью силовых линий – кривых в

пространстве, касательные к которым в каждой точке совпадают с вектором E . Густота силовых линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности,

перпендикулярной силовым линиям, численно равнялось модулю вектора E (рис.2).

		-
	2	3	4
1	2	3
1

Рис.2. Электростатические поля: однородное (1); положительного (2) и отрицательного (3) точечных зарядов; неоднородное (4).

Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных. Поле,

во всех точках которого вектор E имеет одинаковую величину и направление, называется однородным (рис.2(1)). В остальных примерах поля неоднородны.

Поток вектора напряженности электрического поля. Чтобы наглядно ввести это

понятие, рассмотрим сначала поле точечного заряда q с напряженностью	E	q			. Опишем из

		4	o	r 2

этого заряда сферу радиуса r и площадью S 4 r 2 . Величина напряженности измеряется числом силовых линий, проходящих через единицу поверхности сферы, полное число линий, пересекающих сферу равно

ES	q			4 r 2	q		, и не зависит от r! Таким образом, произведение ES (в данном примере это
	4	o	r 2			o

и есть поток) определяется величиной порождающего поле заряда и связано простым соотношением с напряженностью. Здесь уместно сравнить поток вектора напряженности с потоком вектора скорости жидкости, вытекающей из центра сферы равномерно во всех направлениях со скоростью . В этом случае произведение S представляет собой объем жидкости, вытекающий через поверхность сферы наружу в единицу времени. Введем теперь понятие потока вектора строго.


Потоком вектора напряженности электрического поля E через поверхность S называется
величина ФЕ, равная

ФЕ = En dS E cos dS = (E, dS ) ,		(7)

S	S		S
			(рис.3). Вектор
где En – проекция вектора E на направление нормали		n	(рис.3). Вектор

dS имеет величину элементарной площади dS и направление, совпадающее с

направлением нормали n к этой площадке.

Теорема Гаусса. Так называется выражение, связывающее поток ФЕ

вектора E через произвольную замкнутую поверхность S с зарядом внутри нее.

Найдем это выражение. Опишем из точечного заряда q сферу радиуса r. В

каждой точке сферы вектор E направлен перпендикулярно её поверхности и по

величине равен	E	q			. Поэтому поток ФЕ через всю сферу равен

		4	o	r 2


dS
En
	E
dS n	E

Рис.3

ФЕ =

4 r 2

ФЕ =

(8)

Окружим теперь заряд q поверхностью произвольной формы. Тогда поток dФЕ через элемент dS

этой поверхности (рис.4) равен

dÔE EdS cos = 4 o r 2 dS cos 4 o

r 2

4 o dΩ .

Интегрирование в пределах полного телесного угла =4 дает

● ●

dΩ

(9)

Рис. 4

Поток ФЕ равен заряду q внутри поверхности, деленному на о. Если

заряд q находится вне замкнутой поверхности, то ФЕ = 0. Действительно, пучок касательных, проведенных от заряда q (рис.5), делит замкнутую поверхность S на

две части S

и S . Потоки вектора E через эти поверхности равны по

величине, но имеют противоположные знаки, поэтому полный поток

равен нулю.

Пусть теперь внутри замкнутой поверхности находится n

точечных зарядов. По принципу суперпозиции результирующая

Рис.5

напряженность равна векторной сумме напряженностей, создаваемых

каждым зарядом системы в отдельности, следовательно

ÔE (E, dS ) ( Ei

, dS ) (Ei

, dS ) qi

qi ,

S i

i 1 S

i 1 o

(10)

(E, dS )

E n

Это теорема Гаусса: поток вектора напряженности электрического поля ФЕ через любую

замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на о.

Чтобы обобщить теорему Гаусса для непрерывного распределения заряда в пространстве с объемной плотностью , с поверхностной плотностью , или по линии с линейной плотностью , нужно суммирование в (10) заменить интегрированием. Теорема Гаусса используется для вычисления напряженности в случаях, обладающих достаточно высокой симметрией. Для краткости будем называть гауссовой ту (воображаемую, а не заряженную!) замкнутую поверхность S, по которой ведется интегрирование при вычислении потока.

Поле бесконечной равномерно заряженной плоскости. Пусть плоскость равномерно


заряжена с поверхностной плотностью 0. Вектор E должен быть везде
направлен перпендикулярно плоскости от нее. В противном случае
существовала бы составляющая напряженности вдоль плоскости, что					S	n
					S		E
привело бы к перемещению зарядов и противоречило бы предположению о							E
							E
равномерном распределении заряда по плоскости. Также ясно, что во всех
				n
			E				E
точках, равноудаленных от плоскости величина вектора E должна быть
одинакова. Поэтому в качестве гауссовой поверхности логично выбрать						n

прямой цилиндр, расположенный симметрично относительно заряженной
					Рис.6
плоскости, как это показано на рис. 6. Поток вектора E через боковую

поверхность цилиндра равен нулю, так как там векторы E и	n	( dS )


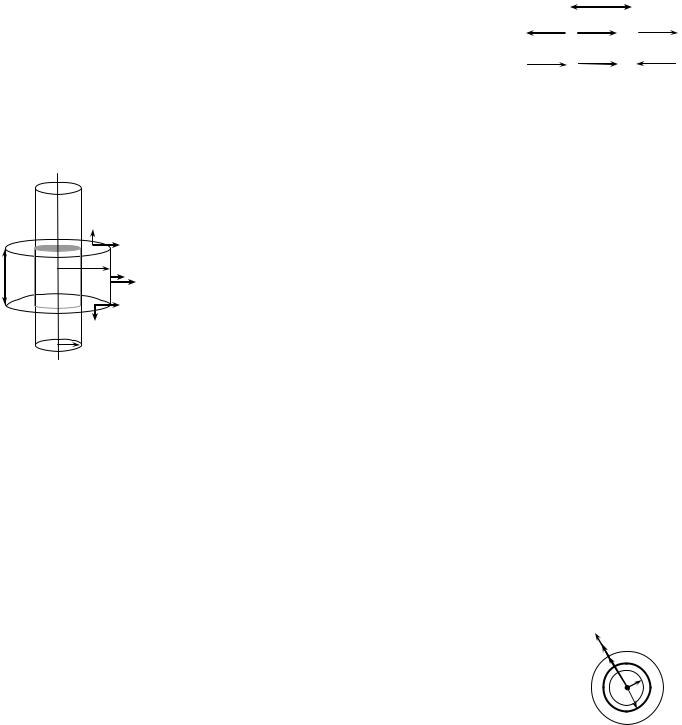
взаимно перпендикулярны, ( E	, dS )=0,	на всей боковой поверхности	(E, dS ) =0. Поэтому

полный поток равен сумме потоков через два основания 2Е S, где S – площадь каждого основания цилиндра (и сечения цилиндра плоскостью тоже). Внутри цилиндра оказался заряд S (показан более плотной штриховкой). По теореме Гаусса 2Е S= S/ о,

(11)

2 o

Следовательно, напряженность не зависит от расстояния до плоскости, и с каждой стороны от

плоскости поле одинаково во всех точках, т.е. однородно.

Поле двух заряженных плоскостей. Пусть две параллельные плоскости равномерно

заряжены с поверхностными плотностями + и - (рис.7). Поле справа и

слева от плоскостей равно нулю (Е= /2 о- /2 о = 0), а между ними (Е=

/2 о+ /2 о = / о), следовательно

Е= / о.

(12)

Такое поле создается в плоском конденсаторе. Если плоскости заряжены

одноименно, то поле между ними равно нулю, а снаружи описывается

формулой (12). И, наконец, если модули не равны: |+ | ≠ |-

|, то поле

будет внутри больше, чем снаружи, но нигде не будет нулевым.

Рис.7

Поле бесконечного равномерно заряженного по поверхности

цилиндра и нити. Пусть поверхность бесконечно длинного цилиндра радиуса R заряжена

равномерно, и на единицу его длины приходится заряд >0. Гауссову

поверхность нужно взять в виде цилиндра высоты h и радиуса r

(изображен пунктиром на рис.8), коаксиального с заряженным. Поток

вектора E через боковую поверхность гауссова цилиндра равен E2 rh, а

через основания – нулю, так как там вектор нормали перпендикулярен

r n

E . Внутрь гауссовой поверхности попадает тонированная часть

заряженного цилиндра, поэтому заряд внутри равен h, поэтому при r>R

по теореме Гаусса имеем E2 rh= h/ о,

, при r>R.

(13)

2 o r

Рис.8

Если R≠0, то при r R, E

. При r<R заряд внутри гауссова

2 o R

цилиндра отсутствует, E2 rh=0, внутри цилиндра напряженность E=0. При R 0, E . Так вблизи тонкого острия можно создавать поля исключительно высокой напряженности, из-за чего заряды начинают стекать с острия в окружающее пространство. Формула (13) подходит и для нити, заряженной с линейной плотностью . В этом случае условие r>R выполняется всегда.

Поле равномерно заряженной сферы. Пусть сфера радиуса R равномерно заряжена (не нужно говорить «по поверхности» - сфера это есть поверхность шара) с поверхностной

плотностью

0. Вследствие центральной симметрии вектор E в любой точке должен быть направлен вдоль

радиуса от центра, а его модуль может зависеть только от расстояния r от центра. В качестве

гауссовой поверхности выберем сферу радиуса r>R (рис.9). По теореме Гаусса поток вектора E

через эту сферу равен E4 r2= 4 R	2
через эту сферу равен E4 r2= 4 R	, вне сферы поле подобно полю точечного				E
o						n
o						r
заряда:						r	r
заряда:
	R2
	R2						R
	E		r 2 ,	(14)			R
	E	o	r 2 ,	(14)
		o

Рис.9

особенно если выразить через полный заряд сферы q и её площадь 4 R2: = q/4 R2, откуда

получим	E	q			. На самой заряженной поверхности Е= / о. При r<R заряда внутри гауссовой

		4	o	r 2

сферы нет, внутри заряженной сферы напряженность Е=0.

Поле равномерно заряженного по объему шара. Пусть шар радиуса R равномерно заряжен с объемной плотностью ρ 0. Гауссову поверхность выберем так же, как для сферы (рис.9) При

r>R, следуя теореме Гаусса, получаем E4 r2= 4 R3 (чтобы найти заряд внутри, мы умножили ρ

3 o

на объем шара радиуса R). Отсюда получим напряженность снаружи и на поверхности шара:

(r≥R).

(15)

3 r 2

При r<R заряд внутрь гауссовой сферы попадает часть заряда шара,

поэтому E4 r2=

4 r 3

, откуда напряженность внутри шара равна

3 o

3,4

(r<R).

(16)

2,3

3 o

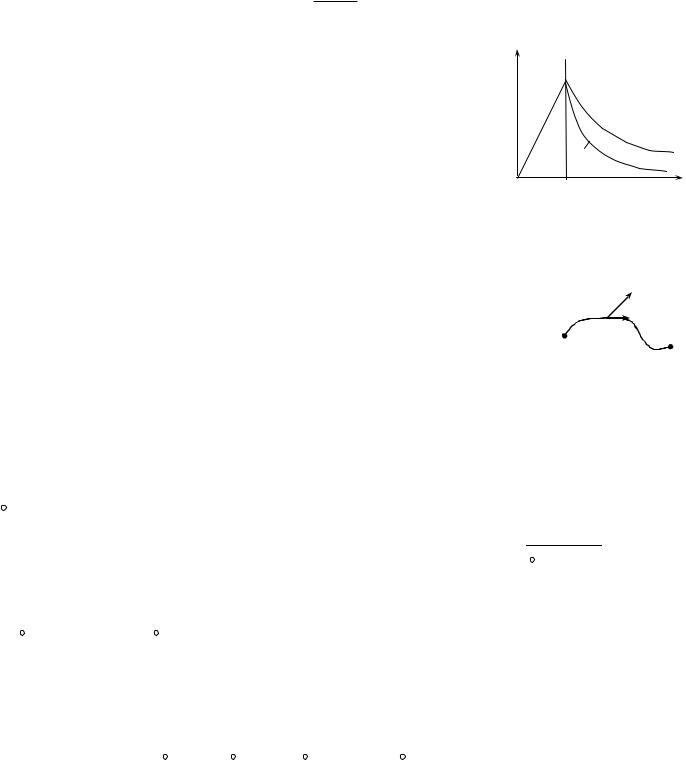
На рис. 10 представлены графики зависимости Е от r для равномерно

Рис.10

заряженных плоскости (1), цилиндра (2), сферы (3) и шара (4).

Теорема о циркуляции вектора E . В курсе механики было доказано, что работа поля

центральных сил зависит только от начального и конечного положений

частицы. Эквивалентным утверждением является: работа такого поля по

перемещению частицы вдоль замкнутой траектории равна нулю. Такие поля

называются потенциальными. Теорема о циркуляции вектора E является

выражением свойства потенциальности электростатического поля. Работа сил

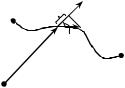
Рис.11

электростатического поля при перемещении точечного заряда q из точки 1 в

точку 2 (рис.11): A (F, dl )

(qE, dl ) q (E, dl ) . Разделим эту работу на q:

(E, dl ) .

(17)

Отношение А/q это работа поля переноса единичного заряда из 1 в 2. Интеграл вида (17), т.е.

(E, dl ) , вычисленный вдоль замкнутой траектории, называется циркуляцией вектора E .

Теорема о циркуляции вектора E утверждает: циркуляция вектора напряженности

электростатического поля по любому замкнутому контуру равна нулю:

(E, dl ) =0.

Доказательство. Электростатическое поле точечного заряда является полем центральных

сил, и, следовательно, потенциальным. Поэтому работа его сил на замкнутом пути равна нулю:

А= (F, dl ) =0,

(E, dl ) 0 . Таким образом, циркуляция поля точечного заряда равна

нулю. Докажем это и для системы n точечных зарядов. По принципу суперпозиции напряженность


E	поля системы точечных зарядов равна: E E1		E2	... En . Умножим это равенство скалярно

на вектор перемещения dl вдоль произвольного замкнутого контура и проинтегрируем по этому

контуру:

(E,dl ) (E1 , dl ) (E2 , dl ) ... (En , dl ) .								(18)

Каждый интеграл в правой части равен нулю как циркуляция вектора напряженности поля отдельного точечного заряда, следовательно, и вся сумма равна нулю. Таким образом, циркуляция

электростатического поля системы n точечных зарядов также равна нулю. Переходя к пределу в (18) нетрудно убедиться, что и для непрерывно распределенного заряда циркуляция электростатического поля равна нулю.

Потенциал. Из независимости от траектории интеграла (E, dl ) следует, что его можно

представить, как убыль некоторой функции координат:

2
1 2 (E, dl ) , или		(19)
1
d (E, dl ) .		(20)

Введенная таким образом функция координат φ( r ) называется потенциалом. Разность потенциалов 1 2 численно равна работе по переносу единичного положительного заряда из

точки 1 в точку 2. Из того, что поле способно совершить такую работу, следует, что в точках 1 и 2 заряд обладает различной потенциальной энергией. Поэтому потенциал можно определить как потенциальную энергию пробного заряда q, отнесенную к его величине (правда саму потенциальную энергию всё равно придется вводить через ту же работу):

(21)

Кроме того, из введенных определений (19,20), а также определения самой потенциальной

энергии, следует, что потенциал определен с точностью до константы.

Потенциал поля точечного заряда. Поскольку заряд q создает

поле с напряженностью (3), скалярное произведение в формуле (20) можно

преобразовать:

(E, dl ) =

dl cos =

=- d

const ,

const , где k

4 o

r 2

Рис.12

и учтено, что dl cos dr (геометрия – на рис.12). Обычно полагают

потенциал при r равным нулю, тогда const =0. В этом случае потенциал поля точечного заряда выражается формулой

					q		.						(22)

					4 o r
													), то точечным следует
Если заряды распределены непрерывно с объемной плотностью ρ( r													), то точечным следует
считать заряд dq dV . Тогда потенциал можно представить интегралом по объему
					1			dV
									.				(23)
					4			r	.				(23)
						o V
Аналогично, если заряды распределены по поверхности или линии, то интегрируют по
поверхности или линии соответственно
1			dS					1				dl
				,								r .	(24)
	4		r	,						4	o	r .	(24)
		o S									o	l

Единицей потенциала является вольт [φ] = [В].

Связь напряженности и потенциала. Пусть dl - вектор малого перемещения вдоль

траектории. Это значит, что радиус-вектор

(x,y,z) получил приращение dl (dx, dy, dz) . Тогда

(E, dl ) = Ex dx Ey dy

Ez dz d ,

(25)

откуда следует, что E

. Вектор

E в декартовых координатах


можно представить суммой E Ex ex		Ey ey	Ez ez

. Дифференциальную

= -

операцию в скобках, примененную к скалярной функции φ, называют градиентом этой функции (grad φ). Обратите внимание: grad φ – это векторная функция, полученная дифференцированием скалярной функции φ! Таким образом, связь напряженности и потенциала выражается формулой



E grad	.	(26)

При решении задач бывает полезно найти проекцию E на направление некоторого вектора l . Так


как (E, dl ) = El dl d , то искомая проекция равна
	E	l	.		(27)
		l	l
			l
	Эквипотенциальные поверхности. Так называются поверхности в пространстве, на
которых потенциал имеет постоянное значение. Чтобы показать, что вектор					всюду
				E	всюду

перпендикулярен эквипотенциальной поверхности, спроектируем его на касательный к этой


поверхности вектор l . Поскольку const на эквипотенциальной поверхности, производная
0 , в соответствии с (27), равна нулю и проекция: E	l		=0. Если в некоторой точке
l	l	l
l		l

проекция вектора на любое касательное направление к поверхности равна нулю, значит, этот

вектор перпендикулярен поверхности. Таким образом, вектор E перпендикулярен

эквипотенциальной поверхности и направлен с учетом знака в сторону максимальной скорости убывания потенциала.

Потенциал системы зарядов. Напряженность поля системы точечных зарядов (6) равна


	E E1 E2	... En .

Умножим это выражение скалярно на вектор dl

(E, dl ) (E1 , dl ) (E2 , dl ) ... (En , dl ) = d 1 d 2 d 3... d n d .

Проинтегрируем это равенство с учетом того, что в знаменателе выражения (22) для потенциала

точечного заряда стоит расстояние от заряда до точки с радиус-вектором r , где вычисляется


потенциал. Для каждого из n точечных зарядов системы это расстояние равно						ri	r	, где	ri	-
радиус-вектор i-го заряда. Следовательно, потенциал поля системы точечных зарядов равен
	1	n		qi
	1			qi
(r )					.					(28)
(r )	4 o				.					(28)
	4 o	i 1	ri	r

Итак, потенциал поля системы точечных зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов, независимо от других.

Чтобы получить потенциальную энергию заряда q в поле системы зарядов qi достаточно потенциал той точки, где находится заряд q умножить на потенциал этой точки

	q	n		qi

Wn q (r )					.	(29)
	4 o

		i 1	ri	r

Потенциальная энергия измеряется работой поля системы зарядов по переносу заряда q из точки с

радиус-вектором r на бесконечность.

Потенциал и напряженность электростатического поля диполя. Диполь – это система

из двух разноименных зарядов, расположенных друг от друга на расстоянии

l r , где

- радиус-вектор произвольной точки А пространства относительно

центра диполя (рис.13). Введем вектор дипольного момента :

●

p ql . Потенциал

в точке А вычислим, как алгебраическую сумму потенциалов зарядов диполя

q(r

r )

-q

. Так как l r , положим

r r

Рис.13

ql cos

p cos

r r

r 2 ;

) l cos . Тогда

( p,er )

. Таким образом,

r 2

потенциал поля диполя равен

p cos

( p,er )

(30)

r 2

Напряженность поля диполя найдем в проекциях на вектор r (Еr) и на перпендикулярное к

направление (E ):

2 p cos

;

p sin

(31)

r 3

Модуль вектора E найдем по теореме Пифагора

E 2 E 2

4cos2 sin 2 ,

r 3

что после подстановки sin2 cos2 1 дает

	p
E	p			1 3cos2	.	(32)

	4	o	r 3
	4		r 3

Напряженность поля диполя убывает обратно пропорционально третьей степени расстояния – быстрее, чем поле точечного заряда. Из (32) легко получить и другие проекции


вектора E : параллельную ( =0) и перпендикулярную оси диполя ( = /2):
EII	2 p			;	E	p			.	(33)

	4	o	r 3			4	o	r 3
		o					o

Постоянный электрический ток

Электрический ток и вектор плотности тока. Ток в проводнике представляет собой направленное движение заряженных частиц. Сила тока (или просто ток) определяется как производная по времени от суммарного заряда Q(t), прошедшего через поперечное сечение проводника к моменту времени t:

			I (t)	dQ(t)	.	(34)
			I (t)		.	(34)
				dt
Средней по сечению проводника плотностью тока называется отношение силы тока к
площади сечения проводника j		I	. В общем случае плотность тока может быть разной в
площади сечения проводника j	ñð	S	. В общем случае плотность тока может быть разной в
	ñð

различных точках сечения. Величина вектора плотности тока численно равна заряду, протекающему в единицу времени через дифференциально малую площадку, перпендикулярную

скорости направленного движения зарядов. За направление вектора плотности тока j

принимается направление средней скорости направленного движения зарядов. В соответствии с этими определениями, при концентрации n частиц в проводнике с зарядом е каждая, и их средней


скорости направленного движения ñð				вектор плотности тока равен

			j en ñð .		(35)	j
						dS
Выделим внутри проводника малую площадку dS (рис.14). Заряд, прошедший						α
							dS
через нее за время dt, равен dq j cos dSdt = ( j, dS )dt , где α – угол между						n

векторами	j	и dS . Заряд dQ , прошедший через все сечение проводника, равен				Рис.14
						Рис.14

интегралу
интегралу	dQ j cos dS dt , откуда ток, протекающий через все сечение
		S

проводника, равен



I ( j, dS )	.	(36)
S

Таким образом, сила тока является потоком вектора плотности тока. Единица силы тока называется ампер [I] = [A] и является основной электрической единицей в системе СИ, ее точное определение будет дано позднее.

Электродвижущая сила (эдс). Если проводник внести в электростатическое поле, то заряды будут двигаться до тех пор, пока их собственное поле не скомпенсирует поле внешнее, после чего практически мгновенно ток прекратится. Для поддержания тока к зарядам необходимо приложить силы не электростатической природы, называемые сторонними. Пусть на некотором

участке цепи действуют сторонние силы с напряженностью E и силы электростатического поля с

напряженностью E . Вычислим работу, необходимую для переноса заряда q из точки 1 в точку 2

. Разделим обе части на q

A12 q(E E ), dl

= qE, dl

+ qE , dl

A12

E, dl

+ E , dl .

Величина

A12

называется напряжением и равна суммарной работе электростатических и

сторонних сил по перемещению единичного положительного заряда из 1 в 2. Первое слагаемое

2	= 1
E, dl	= 1	2 - это введенная ранее разность потенциалов (см.19), а второе называется
1

электродвижущей силой (эдс), которая численно равна работе поля сторонних сил, необходимой для переноса единичного положительного заряда из точки 1 в точку 2

Если точки 1 и 2 совпадают ( 1 2 ) – цепь замкнута, тогда эдс представляет собой циркуляцию вектора напряженности поля сторонних сил. Если на участке не действуют сторонние силы (такой участок называется однородным, эдс=0), то U = 1 2 , для однородного участка цепи напряжение совпадает с разностью потенциалов.


Закон Ома в дифференциальной форме описывает связь между векторами E и						j . Пусть

электрон движется в поле с напряженностью E		. По второму закону Ньютона, он приобретает

				eEt
ускорение a	eE m , а его скорость возрастает по закону o		at o		, где o	- скорость
ускорение a	eE m , а его скорость возрастает по закону o		at o	m	, где o	- скорость
				m

электрона в отсутствии внешнего поля. При каждом столкновении происходит передача кинетической энергии электрона кристаллической решетке, и скорость падает почти до нуля. Усредним выражение для скорости в пределах среднего времени между столкновениями

1 eEt

1 eE

dt o

2 m

Среднее значение скорости o

0 вследствие хаотичности скорости в отсутствие поля.

1 eE

Поэтому

. Учитывая определение

(35), вектор плотности тока

2 m

1 e

2 n

E . Произведение констант, стоящих перед E , также является некоторой константой ,

2 m

Рис.15



j	E	.	(39)

Этот результат называется законом Ома в дифференциальной форме: плотность тока в каждой точке проводника пропорциональна напряженности поля в этой точке. Величина называется проводимостью. Этот закон с высокой точностью выполняется только для металлов.

Часто закон Ома в дифференциальной форме записывают в виде

		1
	j		E	,	(40)


где ρ – удельное сопротивление, которое				с увеличением температуры t, oC по закону:
	возрастает
	o (1 t) ,				(41)

где α – температурный коэффициент сопротивления; ρ и α – табличные величины.

Закон Ома в интегральной форме. В простейшем случае для однородного участка цепи этот закон был установлен экспериментально

I	U	.	(42)

	R

Величина R (сопротивление проводника) зависит от его формы, температуры и материала

R	l	,	(43)
	S

где l – длина, S – площадь поперечного сечения проводника. Единицей сопротивления является ом: [R]=[Ом]. Размерность удельного сопротивления [ρ]=[Ом м].

Рассмотрим неоднородный участок цепи, т.е. содержащий эдс. 1 r R 2 Реальный источник эдс можно рассматривать как идеальный, к которому

последовательно присоединено его внутреннее сопротивление r (рис.15).

Тогда U=I(R+r) (38), закон Ома в интегральной форме

I(R+r)=( 1 2 ) + .

(44)

Произведение силы тока в проводнике на сумму внешнего и внутреннего сопротивлений равно сумме разности потенциалов на концах проводника и действующей в проводнике эдс.

В замкнутой цепи точки 1 и 2 совпадают и 1 2 =0, поэтому закон Ома принимает вид

I
I	R r .	(45)

Когда цепь разомкнута, ток равен нулю, и тогда | 1 2 | = . Эдс источника равна разности

потенциалов на его зажимах при разомкнутой цепи.

Закон Джоуля-Ленца в интегральной форме. Работа А при перемещении заряда q из

2	2	dA	d		dq
точки 1 в точку 2 равна A qEdl q Edl qU . Мощность P				qU		U ,	P IU	.

1	1	dt	dt		dt

(47)

Если на участке нет эдс, и вся работа тока идет на нагревание, то за время dt в проводнике выделится количество теплоты dQ P(t)dt IUdt . Поскольку U IR , dQ I 2 Rdt .

Интегрируя, получим закон Джоуля-Ленца в интегральной форме:

t
Q I 2 Rdt	.	(48)
0

Если ток постоянный, то выражение упрощается: Q I 2 Rt .

Закон Джоуля-Ленца в дифференциальной форме. Вычислим

энергию, которая выделяется в малом объеме проводника dV, предполагая для

простоты, что векторы j	↑↑ E	↑↑ dl (рис.16). При перемещении заряда dq на

dl поле совершает работу dA dqEdl . Подставим из закона Ома E j , и

		dS
		E
j

	dl
	Рис.16

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.2015360.6 Кб79Лекции по приводу.pdf
#
09.02.20151.32 Mб42Лекции по физике 3 семестр.doc
#
09.02.2015611.84 Кб353Лекции_ООП_ИС.doc
#
22.11.2018345.09 Кб3Лекции_Принятие решений.doc
#
23.09.2019445.44 Кб13Лекции_Россия_XX век.doc
#
09.02.20151.22 Mб11Лекции_ЭиМ.pdf
#
09.02.201555.49 Кб8лекции_экономика.docx
#
15.11.20192.98 Mб5Лекционный материал - 2.DOC
#
10.11.2018186.37 Кб0ЛЕКЦИЯ 04 Б.doc
#
12.07.2019107.52 Кб5ЛЕКЦИЯ 05 Б.doc
#
10.11.2019198.66 Кб11лекция 1 бухучет.doc