Исследование булевой функции на принадлежность к основным классам замкнутости

Перечисленные ниже пять классов замкнутости называются так, поскольку при подстановке одной функции этого класса в другую результат остаётся функцией этого класса.

Множество функций, сохраняющих 0. Определяется условием f (0, 0, 0) = 0. (Определение приведено для булевых функций от трёх переменных, но его легко обобщить на случай произвольного количества переменных).

Множество функций, сохраняющих 1. Определяется условием f (1, 1, 1) = 1.

Линейные. Множество функций, многочлен Жегалкина которых не содержит произведений.

Монотонные. Выполнено условие: если набор α меньше набора β, то f (α) ≤ f (β).

Уточнение: для сравнения наборов используется правило - набор α меньше набора β тогда и только тогда, когда каждый элемент α не больше соответствующего элемента β, и хотя бы один элемент α меньше соответствующего элемента β.

Например, набор (0, 1, 0) меньше набора (1, 1, 1). А про наборы (1, 1, 0) и (1, 0, 1) нельзя сказать, что один меньше другого.

Для проверки функции на монотонность используют рисунок, называемый диаграммой Хассе.

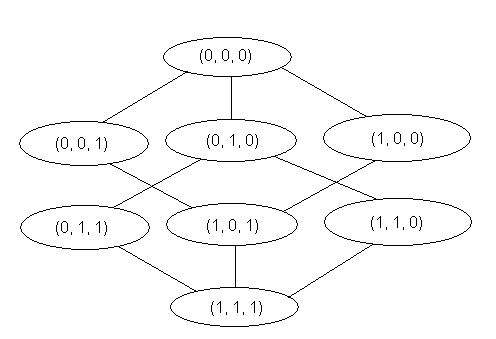
Идея здесь состоит в том, чтобы сравнивать не каждый два набора из восьми, а меньшее количество пар. Возле каждого набора переменных пишем значение функции на этом наборе.

При этом, если будет нарушение монотонности, оно обнаружится на диаграмме.

Например, для функции нарушение монотонности происходит следующим образом: (0, 0, 1) < (0, 1, 1), но f (0, 0, 1) > f (0, 1, 1), поскольку f (0, 0, 1) =1, f (0, 1, 1) = 0.

Наконец, самодвойственной называют булеву функцию, которая равна двойственной к ней.

Ответ на задачу о проверке принадлежности булевой функции к классам замкнутости записывают так:

	T0	T1	L	M	S
f	+	+	–	–	–
	–	–	–	–	–

Здесь T0 означает функции, сохраняющие 0, T1 – функции, сохраняющие 1, L – линейные, M – монотонные, S – самодвойственные.

Ответ в таблице приведён, разумеется, для функции .

Применение теоремы Пóста

(Ознакомительный материал!)

Перед решением заключительной задачи про булевы функции вспомним формулировку теоремы Пóста: если в наборе булевых функций есть хотя бы одна не сохраняющая 0, хотя бы одна не сохраняющая 1, хотя бы одна нелинейная, хотя бы одна немонотонная и хотя бы одна несамодвойственная, то через функции этого набора можно выразить все остальные булевы функции.

Иногда эту теорему формулируют более кратко: если класс булевых функций не лежит целиком ни в одном из пяти основных классов замкнутости, то из этого класса можно выразить все булевы функции.

Выражать каждую булеву функцию неудобно, поэтому можем ограничиться получением конъюнкции и отрицания.

Если мы это сделаем, то сможем получить дизъюнкцию через отрицание и конъюнкцию, а затем каждую булеву функцию через её СДНФ.