
- •Методы вычисления пределов
- •Предел функции
- •Окрестность точки
- •Предел функции в точке. Непрерывность функции в точке
- •Предел функции на бесконечности
- •Бесконечно большая и бесконечно малая функции
- •Односторонние пределы
- •Элементарные функции
- •Вычисление пределов
- •Правила предельного перехода
- •Предел дробно-рациональной функции
- •Предел функций, содержащих иррациональные выражения
- •Замечательные пределы. Эквивалентные бесконечно малые функции
- •Пределы, содержащие тригонометрические функции
- •Пределы выражений, содержащих показательную, логарифмическую и степенную функции
- •Предел показательно-степенной функции
- •197376, С.-Петербург, Проф. Попова, 5
Пределы, содержащие тригонометрические функции
При вычислении пределов, содержащих тригонометрические функции, как правило, приходится обращаться к таблице эквивалентностей, предварительно преобразовав выражение с помощью тригонометрических формул.
Пример 2.20. Вычислить .
.
Решение. 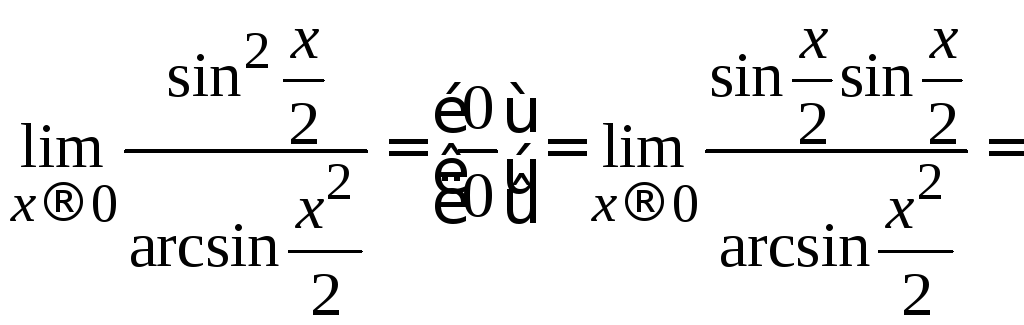
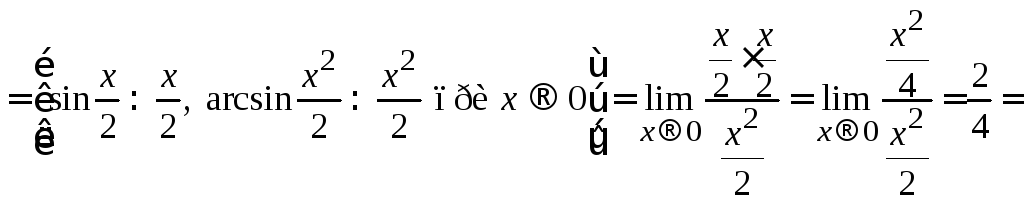
![]() .
.
Пример 2.21. Вычислить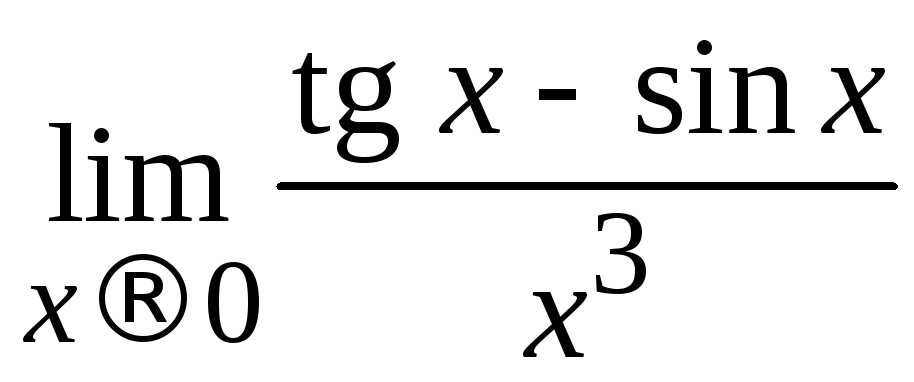 .
.
Решение. Вычислить этот предел в 2.4 не удалось. Рассмотрим другой путь рассуждений. С помощью преобразований перейдем в числителе от разности бесконечно малых к произведению бесконечно малых и заменим эквивалентными в произведении.

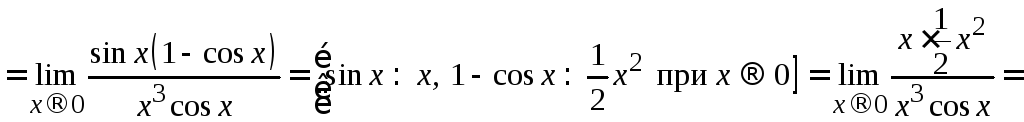
![]()
![]() .
.
В некоторых случаях применение тригонометрических преобразований позволяет раскрыть неопределенность, не обращаясь к таблице эквивалентностей.
Пример 2.22. Вычислить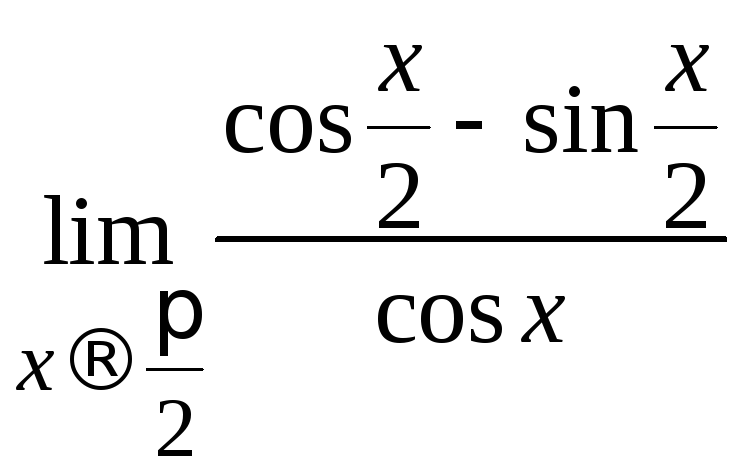 .
.
Решение. Так как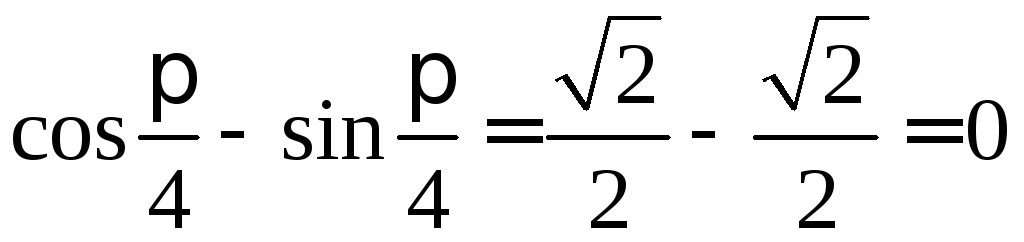 и
и![]() ,
то имеем неопределенность
,
то имеем неопределенность![]() .
Имеет смысл преобразовать знаменатель
по формуле
.
Имеет смысл преобразовать знаменатель
по формуле![]() ,
а потом разложить знаменатель на
множители как разность квадратов. После
сокращения общего множителя в числителе
и знаменателе, неопределенность уйдет:
,
а потом разложить знаменатель на
множители как разность квадратов. После
сокращения общего множителя в числителе
и знаменателе, неопределенность уйдет:
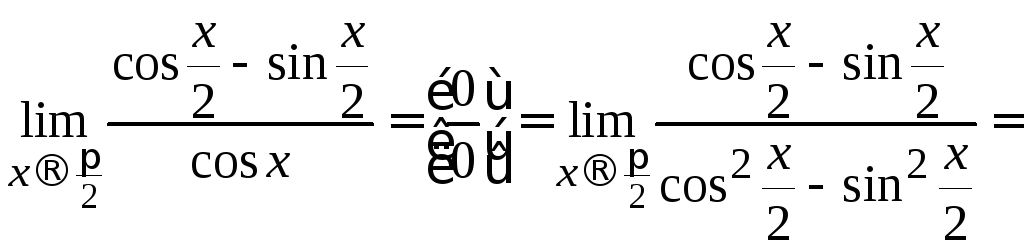
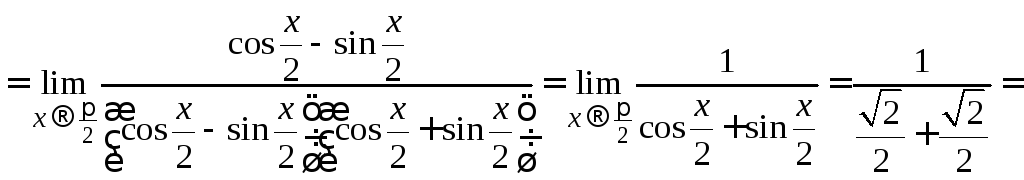
![]() .
.
Пример 2.23. Вычислить .
.
Решение. Известно, что![]() .
Выражение, стоящее под знаком предела,
дает неопределенность
.
Выражение, стоящее под знаком предела,
дает неопределенность![]() при
при![]() .
Уничтожить неопределенность только
посредством преобразований, как это
было сделано примере 2.22, не удастся.
Сделаем замену переменной так, чтобы
новая переменная стремилась к нулю.
Положим
.
Уничтожить неопределенность только
посредством преобразований, как это
было сделано примере 2.22, не удастся.
Сделаем замену переменной так, чтобы
новая переменная стремилась к нулю.
Положим![]() ,
,![]() при
при![]()
![]() ,
а
,
а![]() .
Далее воспользуемся формулой приведения
.
Далее воспользуемся формулой приведения :
:
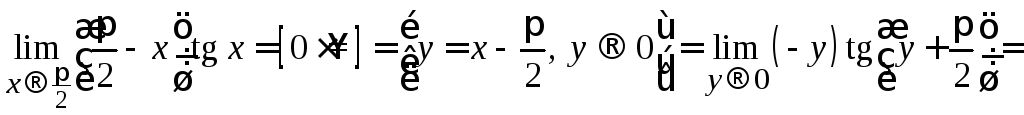
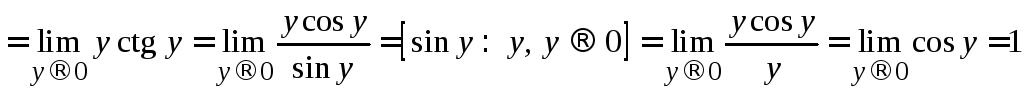 .
.
Замечание. Предел![]() также вычисляется путем замены
переменной:
также вычисляется путем замены
переменной:![]() и последующим применением формул
приведения. Однако было бы ошибкой
сразу прибегнуть к таблице эквивалентностей:
и последующим применением формул
приведения. Однако было бы ошибкой
сразу прибегнуть к таблице эквивалентностей:![]()
![]() .
Дело в том, что аргументы данных функций
–
.
Дело в том, что аргументы данных функций
–![]() и
и![]() не являются бесконечно малыми при
не являются бесконечно малыми при![]() .
.![]()
Пределы выражений, содержащих показательную, логарифмическую и степенную функции
Пример 2.24. Вычислить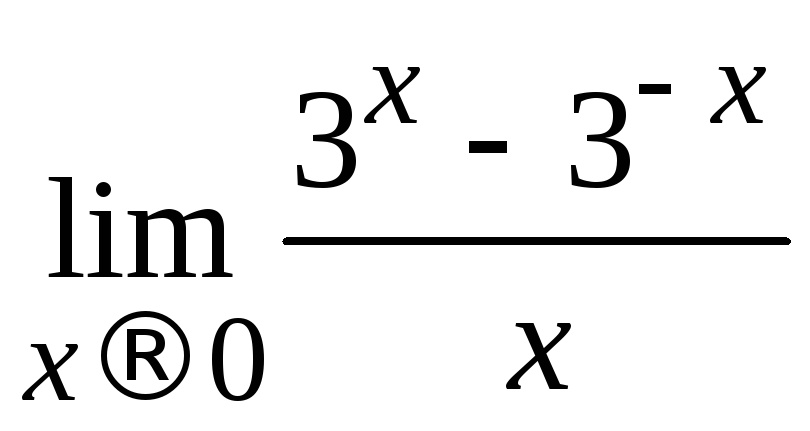 .
.
Решение. Так как![]() ,
то выражение, стоящее под знаком предела,
при
,
то выражение, стоящее под знаком предела,
при![]() дает неопределенность
дает неопределенность![]() .
Воспользуемся свойствами показательной
функции:
.
Воспользуемся свойствами показательной
функции:![]()
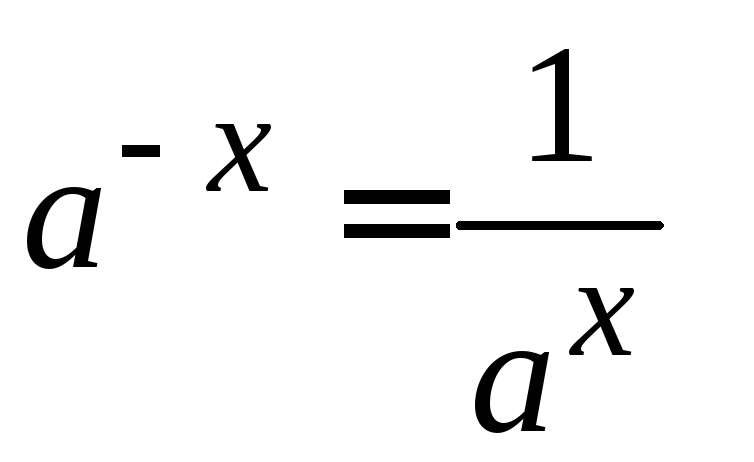 и преобразуем числитель дроби следующим
образом:
и преобразуем числитель дроби следующим
образом: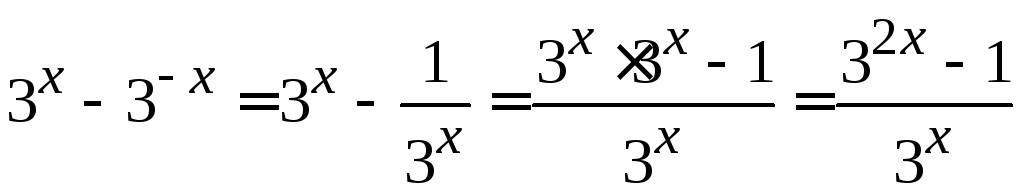 .
Тогда
.
Тогда
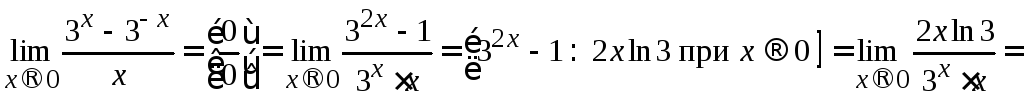
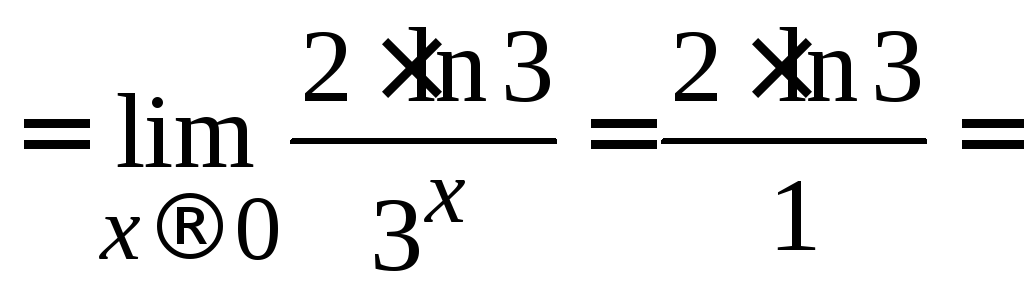
![]() .
.
Пример 2.25. Вычислить![]() .
.
Решение. В скобках воспользуемся
свойством логарифмической функции: и выделим в аргументе логарифма единицу:
и выделим в аргументе логарифма единицу: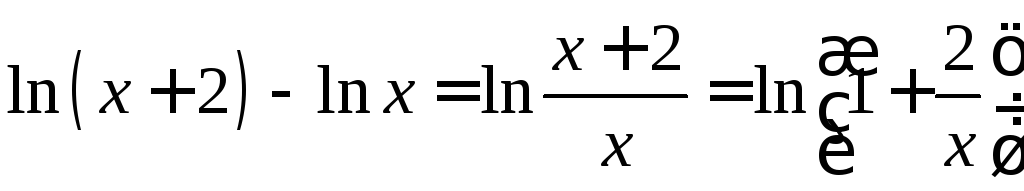 Легко видеть, что
Легко видеть, что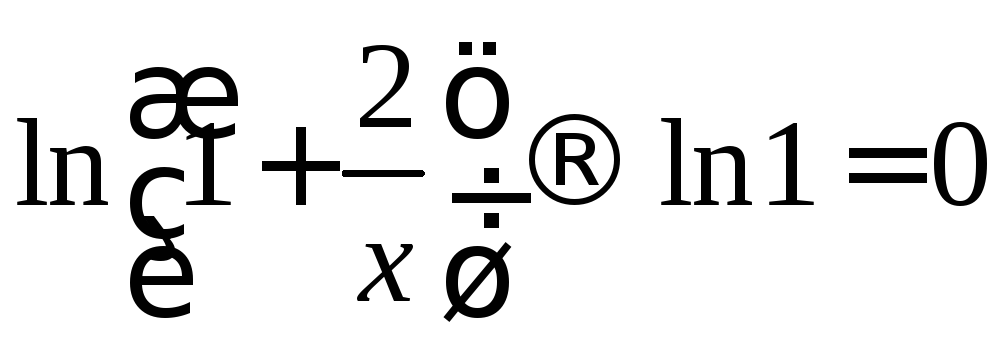 ,
а выражение
,
а выражение![]() при
при![]() .
По таблице эквивалентностей имеем:
.
По таблице эквивалентностей имеем: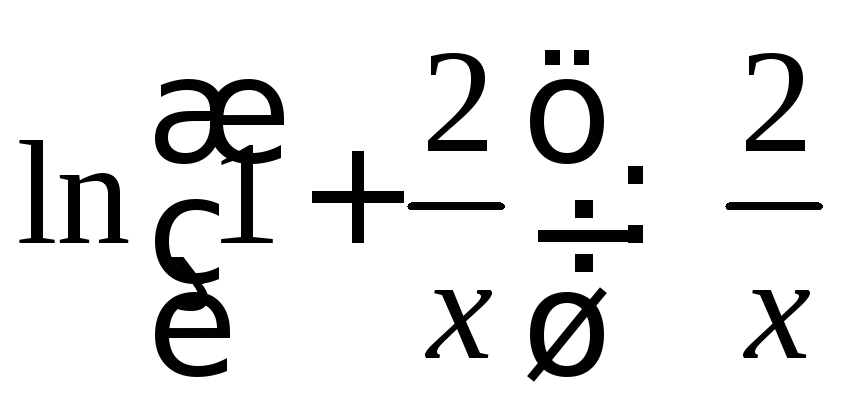 при
при![]() ,
,![]() =
=
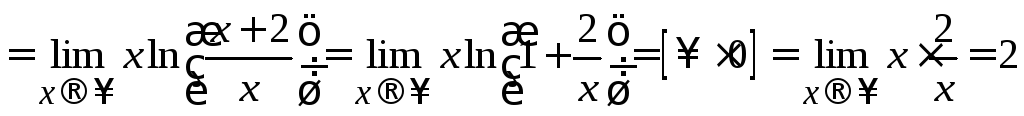 .
.
Пример 2.26. Вычислить![]() .
.
Решение.Поскольку по определению
логарифма![]() ,
надо раскрыть неопределенность
,
надо раскрыть неопределенность![]() .
Введем новую переменную, так чтобы
она стремилась к нулю и сделаем замену
в пределе:
.
Введем новую переменную, так чтобы
она стремилась к нулю и сделаем замену
в пределе:
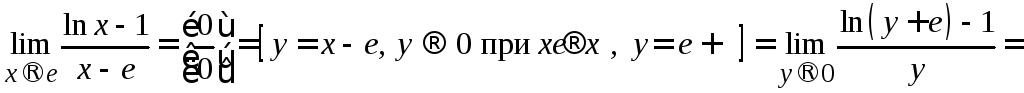

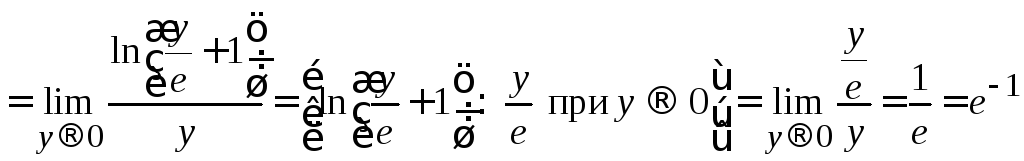 .
.
Пример 2.27. Вычислить .
.
Решение.
Применим к степенным выражениям
соотношение
![]() и сделаем в пределе замену
и сделаем в пределе замену![]() с целью воспользоваться эквивалентностью
с целью воспользоваться эквивалентностью![]() при
при![]() .
Тогда
.
Тогда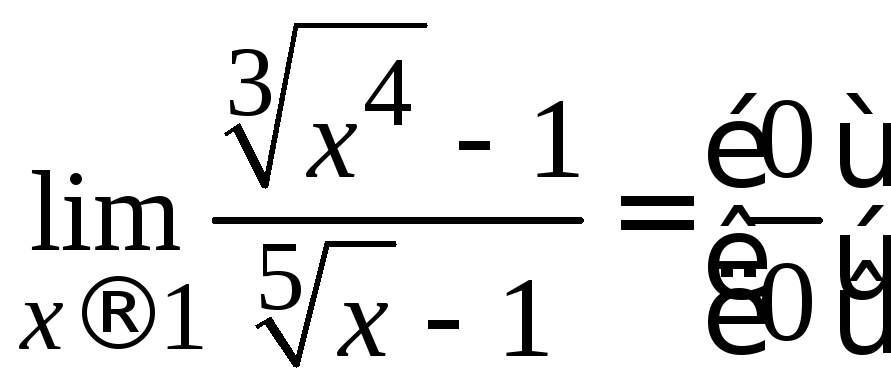 =
=
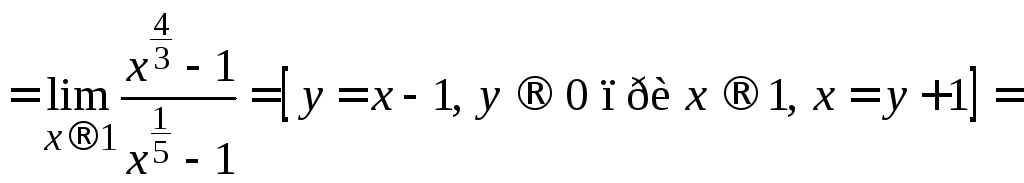
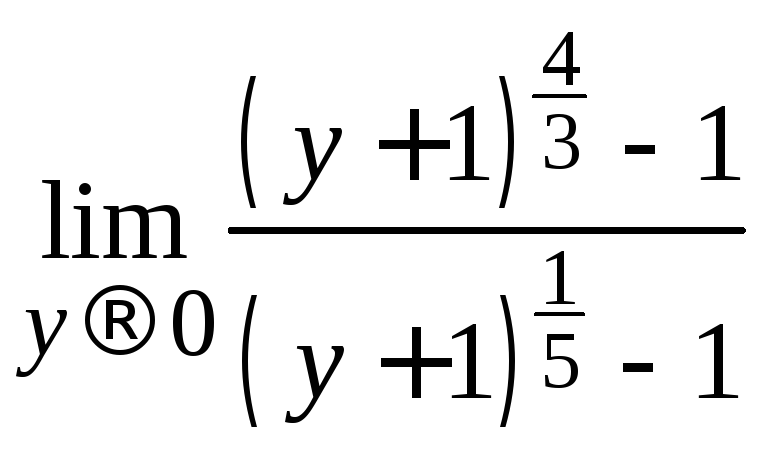 =
=
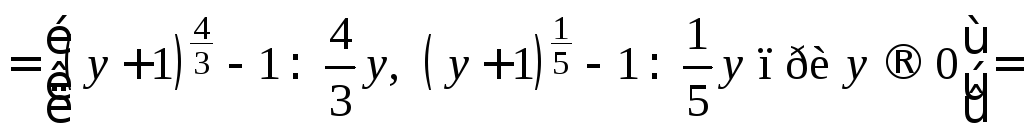
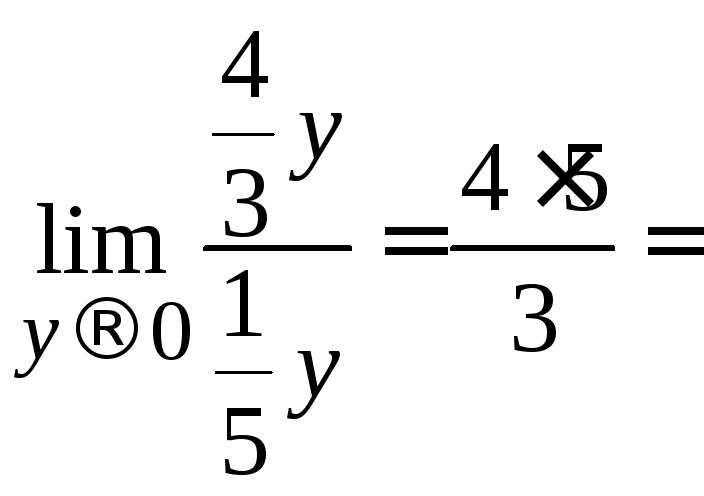
![]() .
.
Предел показательно-степенной функции
Напомним, что функция
![]() ,
основание и показатель степени которой
являются функциями, зависящими от
переменной
,
основание и показатель степени которой
являются функциями, зависящими от
переменной![]() ,
называется показательно-степенной.
Пользуясь тождеством
,
называется показательно-степенной.
Пользуясь тождеством![]() и свойством логарифмической функции
и свойством логарифмической функции![]() ,
представим показательно-степенную
функцию в виде
,
представим показательно-степенную
функцию в виде![]() .
В силу непрерывности показательной
функции по формуле (2.6) получаем:
.
В силу непрерывности показательной
функции по формуле (2.6) получаем:
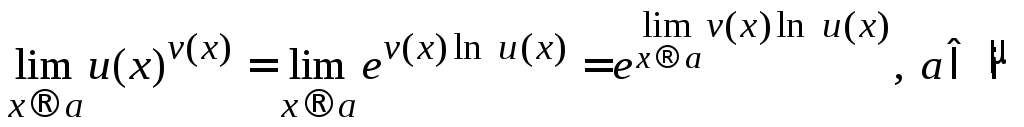 .
(2.10)
.
(2.10)
Таким образом, нахождение исходного
предела сводится к нахождению предела
![]() .
Показательно-степенные выражения в
пределе могут порождать три типа
неопределенности:
.
Показательно-степенные выражения в
пределе могут порождать три типа
неопределенности:![]() ,
,![]() ,
,![]() .
Для раскрытия неопределенности
.
Для раскрытия неопределенности![]() можно использовать второй замечательный
предел
можно использовать второй замечательный
предел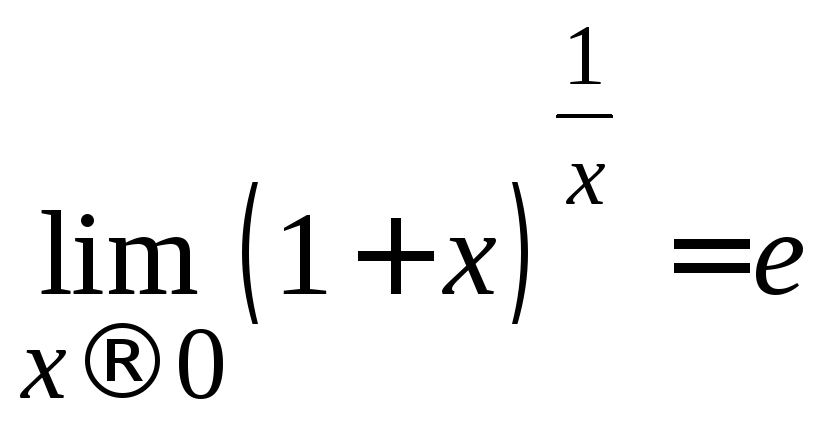 .
.
Правила вычисления
![]() :
:
1. Если функции ![]() и
и![]() имеют при
имеют при![]() конечные пределы, то справедливо
соотношение
конечные пределы, то справедливо
соотношение
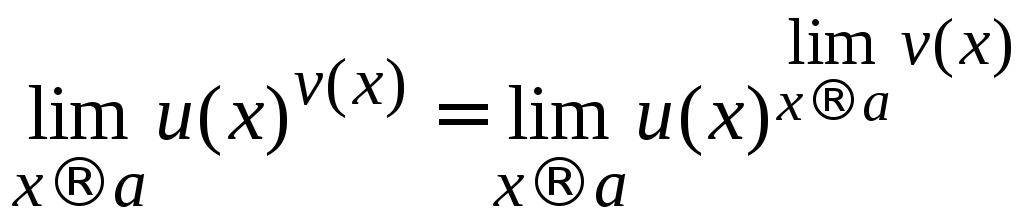 .
(2.11)
.
(2.11)
2. Во всех остальных случаях рекомендуется
перейти к основанию
![]() по формуле (2.10), вычислить предел
по формуле (2.10), вычислить предел![]() и воспользоваться свойствами показательной
функции
и воспользоваться свойствами показательной
функции![]() .
.
Пример 2.28. Вычислить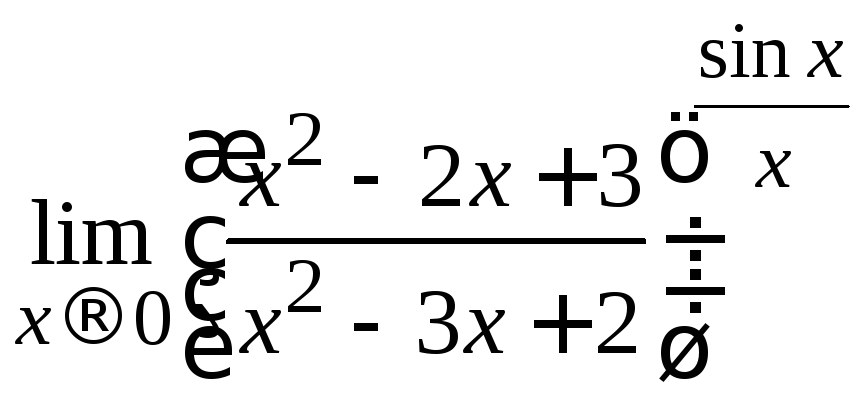 .
.
Решение. Так как основание
и показатель степени имеют при![]() конечные пределы:
конечные пределы: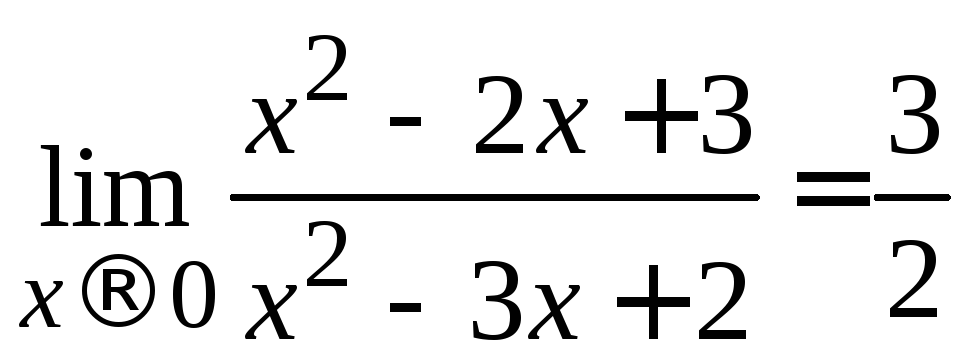 ,
,![]() ,
то по формуле (2.10) получаем:
,
то по формуле (2.10) получаем:
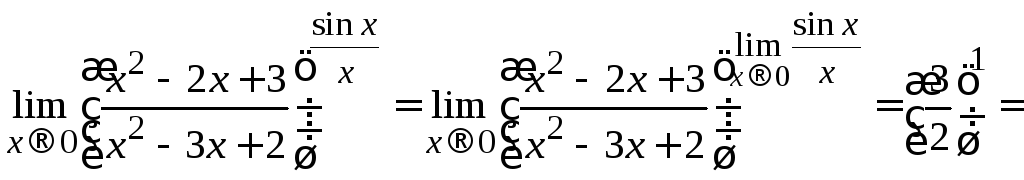
![]() .
.
Пример 2.29. Вычислить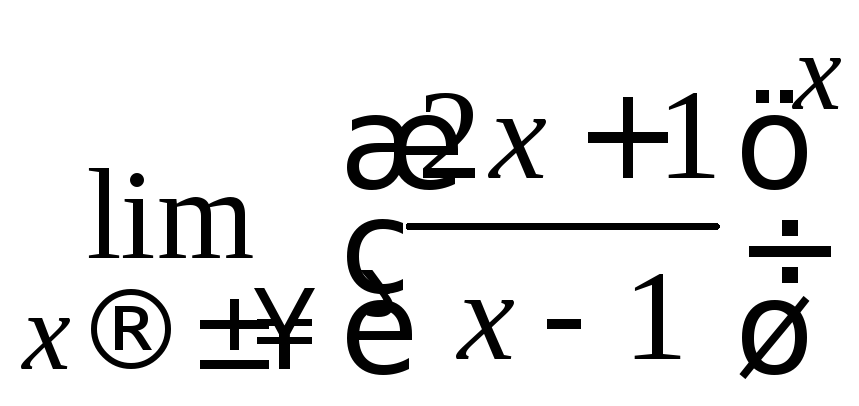 .
.
Решение.Согласно формуле (2.7)![]() .
Пользуясь свойствами показательной
функции с основанием, большим единицы:
.
Пользуясь свойствами показательной
функции с основанием, большим единицы:![]() и
и![]() ,
окончательно получаем:
,
окончательно получаем:
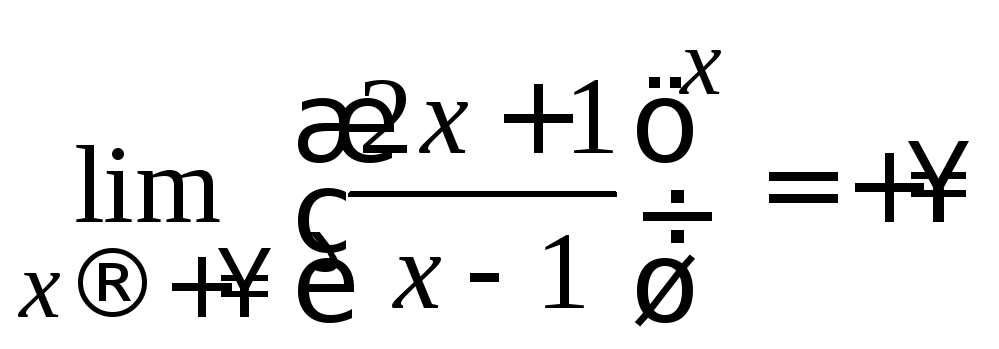 и
и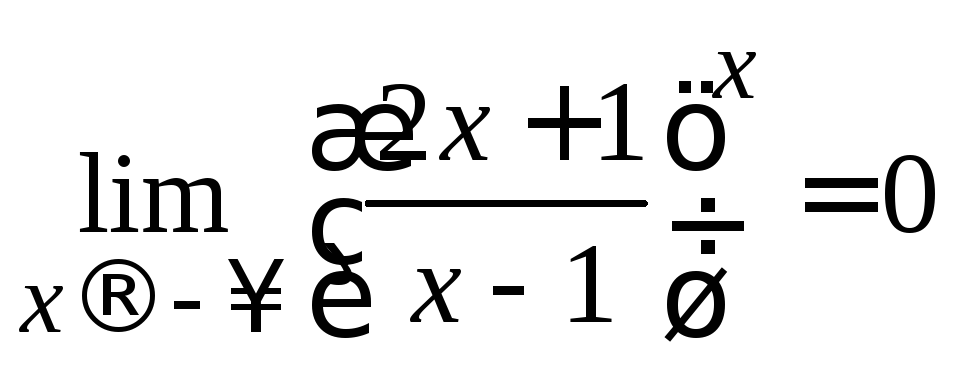 .
.
Пример 2.30. Вычислить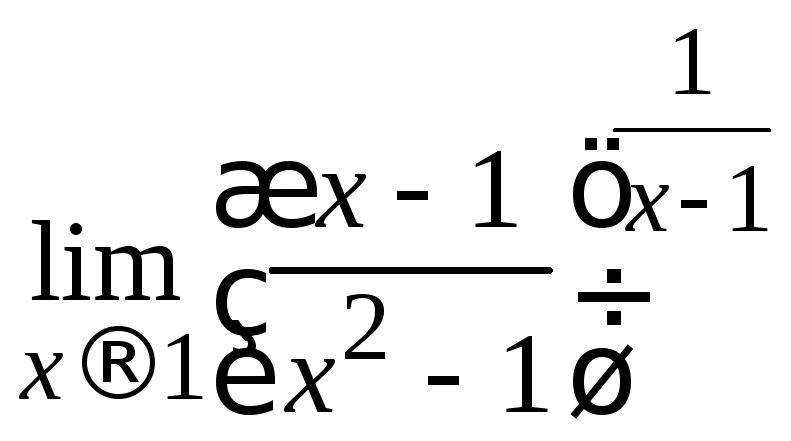 .
.
Решение.Найдем пределы основания
и показателя степени при![]() :
:
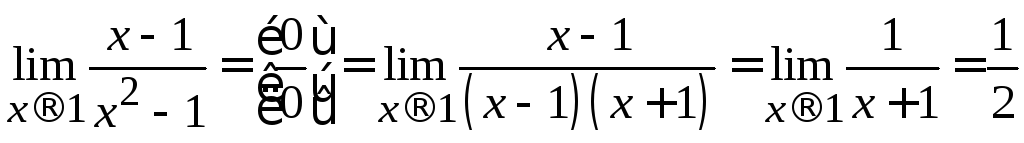 ;
;![]() .
.
Однако поведение показательной функции
на бесконечности существенно зависит
от знака бесконечно удаленной точки.
Для показательной функции с основанием,
меньшим единицы, имеем: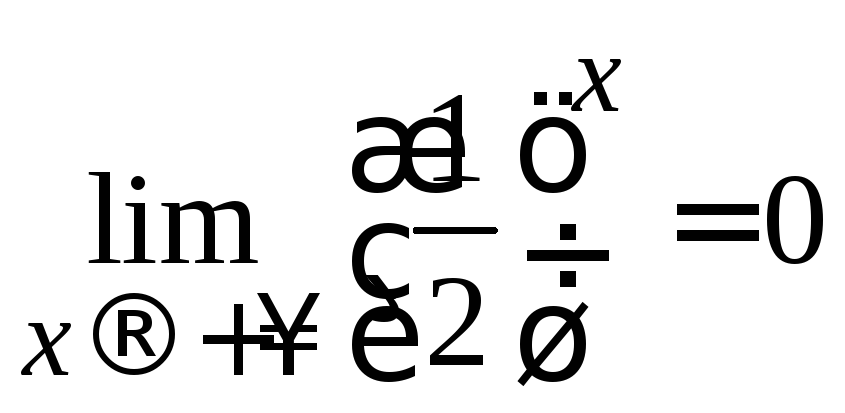 и
и .
Проанализируем поведение функции
.
Проанализируем поведение функции![]() при
при![]() .
Если
.
Если![]() стремится
к 1 справа, т. е. оставаясь все время
больше 1, то разность
стремится
к 1 справа, т. е. оставаясь все время
больше 1, то разность![]() стремится к нулю, также оставаясь
положительной. Следовательно,
стремится к нулю, также оставаясь
положительной. Следовательно,![]() .
При стремлении
.
При стремлении![]() к 1 слева
к 1 слева![]() будет меньше 1, а разность
будет меньше 1, а разность![]() стремится к нулю, оставаясь отрицательной.
В этом случае
стремится к нулю, оставаясь отрицательной.
В этом случае![]() .
Тогда предел исходной показательно-степенной
функции будет зависеть от того, с какой
стороны
.
Тогда предел исходной показательно-степенной
функции будет зависеть от того, с какой
стороны![]() приближается
к 1:
приближается
к 1:
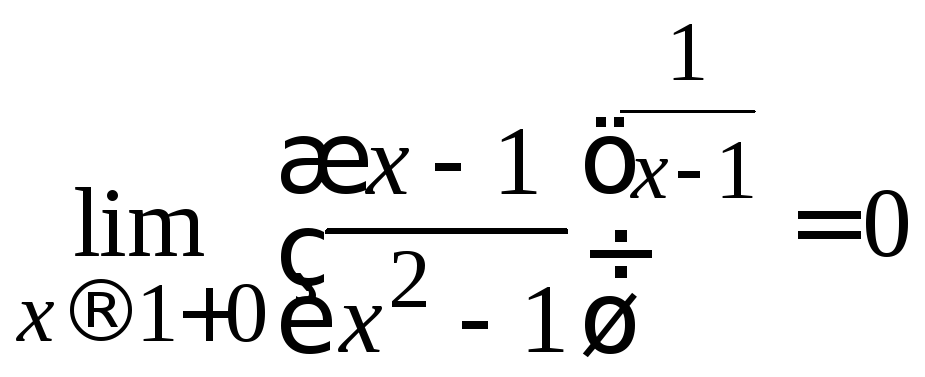 и
и
![]() .
.
Пример 2.31. Вычислить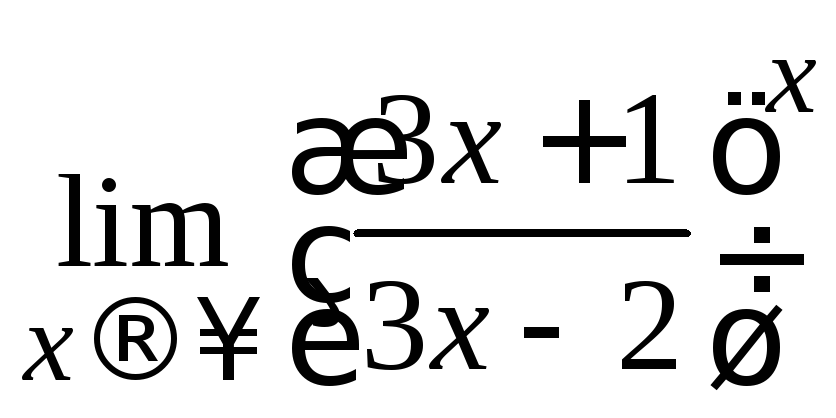 .
.
Решение. Неопределенность![]() можно раскрыть, не прибегая к формуле
(2.10), а пользуясь вторым замечательным
пределом. Воспользуемся свойством
показательной функции
можно раскрыть, не прибегая к формуле
(2.10), а пользуясь вторым замечательным
пределом. Воспользуемся свойством
показательной функции![]() и преобразуем выражение, стоящее под
знаком предела, следующим образом:
и преобразуем выражение, стоящее под
знаком предела, следующим образом:
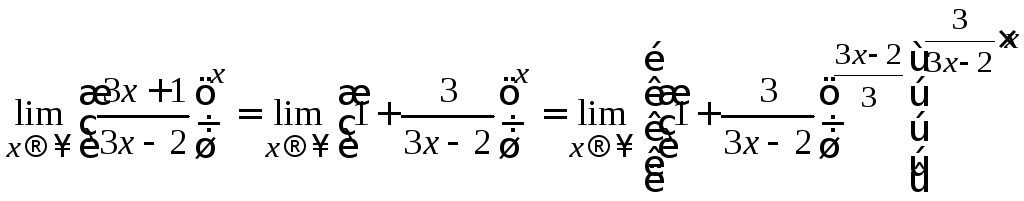 .
.
По второму замечательному пределу (2.9) имеем:
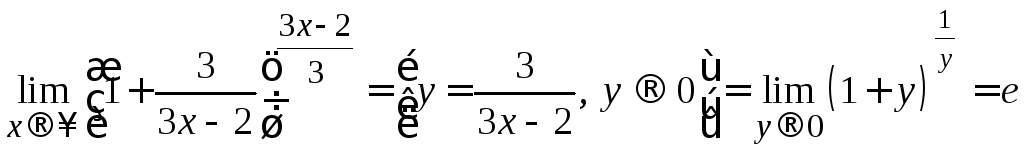 .
.
Кроме того,
![]() .
Тогда по формуле (2.11) окончательно
получаем:
.
Тогда по формуле (2.11) окончательно
получаем:
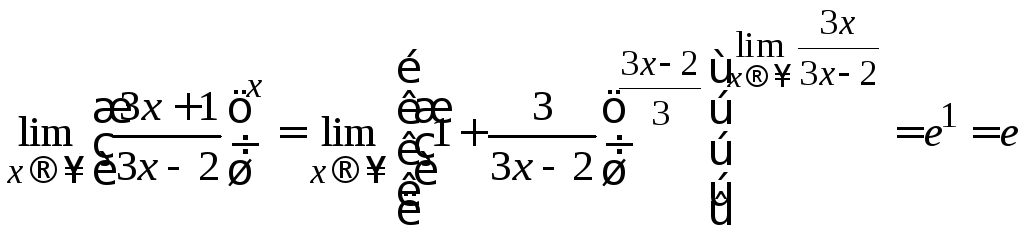
Список литературы
1. Письменный Д. Т. Конспект лекций по высшей математике: В 2 ч. М.: Айрис Пресс, 2006. Ч. 1.
2. Комплексные числа и многочлены: Методические указания к решению задач / Сост.: М. Н. Абрамова, Е. А. Толкачева, А. И. Куприянов. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2007.
Содержание
1. ПРЕДЕЛ ФУНКЦИИ 4
1.1. Окрестность точки 4
1.2. Предел функции в точке. Непрерывность функции в точке 5
1.3. Предел функции на бесконечности 6
1.4. Бесконечно большая и бесконечно малая функции 7
1.5. Односторонние пределы 8
1.6. Элементарные функции 9
2. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ 12
2.1. Правила предельного перехода 12
2.2. Предел дробно-рациональной функции 16
2.3. Предел функций, содержащих иррациональные выражения 20
2.4. Замечательные пределы. Эквивалентные бесконечно малые функции 23
2.5. Пределы, содержащие тригонометрические функции 27
2.6. Пределы выражений, содержащих показательную, логарифмическую и степенную функции 30
2.7. Предел показательно-степенной функции 31
Редактор И. Г. Скачек
__________________________________________________________________
Подписано в печать Формат 6084 1/16. Бумага офсетная.
Печать офсетная. Печ. л. 2.0.
Гарнитура «Times». Тираж 250 экз. Заказ
__________________________________________________________________
Издательство СПбГЭТУ «ЛЭТИ»
