
- •Методы вычисления пределов
- •Предел функции
- •Окрестность точки
- •Предел функции в точке. Непрерывность функции в точке
- •Предел функции на бесконечности
- •Бесконечно большая и бесконечно малая функции
- •Односторонние пределы
- •Элементарные функции
- •Вычисление пределов
- •Правила предельного перехода
- •Предел дробно-рациональной функции
- •Предел функций, содержащих иррациональные выражения
- •Замечательные пределы. Эквивалентные бесконечно малые функции
- •Пределы, содержащие тригонометрические функции
- •Пределы выражений, содержащих показательную, логарифмическую и степенную функции
- •Предел показательно-степенной функции
- •197376, С.-Петербург, Проф. Попова, 5
Предел функции на бесконечности
Пусть функция
![]() определена на всей числовой оси.
Определение предела функции
определена на всей числовой оси.
Определение предела функции![]() при
при![]() см. в [1, с. 114].
см. в [1, с. 114].
Обозначение:
![]() .
.
Запишем определение предела функции коротко:
![]() .
.
Г еометрический
смыслэтого определения: для любой‑окрестности
точки
еометрический
смыслэтого определения: для любой‑окрестности
точки![]() (рис. 1.4) найдется такая окрестность
бесконечно удаленной точки
(рис. 1.4) найдется такая окрестность
бесконечно удаленной точки![]() (ось
(ось![]() ),
что для всех точек этой окрестности
соответствующие значения функции
),
что для всех точек этой окрестности
соответствующие значения функции![]() лежат в
лежат в![]() -окрестности
точки
-окрестности
точки![]() ,
т. е. точки графика функции
,
т. е. точки графика функции![]() лежат внутри полосы шириной
лежат внутри полосы шириной![]() ,
ограниченной прямыми
,
ограниченной прямыми![]() ,
,![]() .
.
Если рассматривается поведение функции
при
![]() или при
или при![]() ,
то пишут
,
то пишут![]() и, соответственно,
и, соответственно,![]() .
.
Бесконечно большая и бесконечно малая функции
Пусть
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() .
Определение бесконечно большой функции
при
.
Определение бесконечно большой функции
при![]() см. в [1, с. 114].
см. в [1, с. 114].
Обозначение:
![]() .
Запишем определение коротко:
.
Запишем определение коротко:
![]() .
.
Г еометрический
смыслопределения: для любой окрестности
бесконечно удаленной точки
еометрический
смыслопределения: для любой окрестности
бесконечно удаленной точки![]() найдется такая
найдется такая![]() -окрестность
точки
-окрестность
точки![]() ,
что для всех точек этой окрестности,
кроме точки
,
что для всех точек этой окрестности,
кроме точки![]() ,
соответствующие значения функции
,
соответствующие значения функции![]() лежат в окрестности
лежат в окрестности![]() ,
т. е. точки графика лежат выше прямой
,
т. е. точки графика лежат выше прямой![]() и ниже прямой
и ниже прямой![]() (рис. 1.5).
(рис. 1.5).
Если функция
![]() стремится к бесконечности при
стремится к бесконечности при![]() ,
принимая только положительные значения,
то пишут
,
принимая только положительные значения,
то пишут![]() ,
а если, принимая лишь отрицательные
значения, то пишут
,
а если, принимая лишь отрицательные
значения, то пишут![]() .
.
Пусть функция
![]() определена на всей числовой оси.
Определение бесконечно большой функции
при
определена на всей числовой оси.
Определение бесконечно большой функции
при![]() см. в [1, с. 114].
см. в [1, с. 114].
О бозначение:
бозначение:![]() .
Коротко:
.
Коротко:
Геометрический смыслопределения:
для любой окрестности![]() бесконечно удаленной точки оси
бесконечно удаленной точки оси![]() найдется такая окрестность
найдется такая окрестность![]() бесконечно удаленной точки оси
бесконечно удаленной точки оси![]() ,
что как только точка попадает в эту
окрестность, так сразу соответствующие
значения функции
,
что как только точка попадает в эту
окрестность, так сразу соответствующие
значения функции![]() лежат в окрестности
лежат в окрестности![]() ,
т. е. точки графика лежат выше прямой
,
т. е. точки графика лежат выше прямой![]() и ниже прямой
и ниже прямой![]() (рис. 1.6).
(рис. 1.6).
Определение[1, с. 115]. Функция![]() называется бесконечно малой при
называется бесконечно малой при![]() (включая бесконечность), если
(включая бесконечность), если![]() .
.
Односторонние пределы
В определении предела функции при
определении предела функции при![]() считается, что
считается, что![]() стремится к
стремится к![]() любым способом: справа (оставаясь
больше
любым способом: справа (оставаясь
больше![]() ),
слева (оставаясь меньше
),
слева (оставаясь меньше![]() )
или колеблясь около точки
)
или колеблясь около точки![]() .
Часто способ приближения
.
Часто способ приближения![]() к
к![]() влияет на значение предела функции,
поэтому вводят понятие односторонних
пределов.
влияет на значение предела функции,
поэтому вводят понятие односторонних
пределов.
Если
![]() стремится к
стремится к![]() справа, то пишут:
справа, то пишут:![]() ,
если же
,
если же![]() стремится к
стремится к![]() слева, то пишут:
слева, то пишут:![]() .
.
Пример 1.1. Найдите односторонние
пределы функции, заданной рис. 1.7, при![]() .
.
Решение.На рис. 1.7 приведен график
функции, для которой
![]() ,
а
,
а
![]() .
.
Элементарные функции
Рассмотрим поведение основных элементарных функций на примерах.
Постоянная функция
![]() и степенная функция
и степенная функция![]() непрерывны во всех точках числовой оси
(см. 1), то есть
непрерывны во всех точках числовой оси
(см. 1), то есть
![]() (1.1)
(1.1)
Пример 1.2.Найдите![]() .
.
Решение.При![]() степенная функция является бесконечно
большой (см. 1.4), причем ее предел
зависит не только от поведения аргумента
степенная функция является бесконечно
большой (см. 1.4), причем ее предел
зависит не только от поведения аргумента![]() ,
но и от четности или нечетности показателя
степени
,
но и от четности или нечетности показателя
степени![]() ,
так как
,
так как![]()
![]() .
Но при этом
.
Но при этом![]() ,
,![]() .
.
Значит,
 а
а![]() (1.2)
(1.2)
Функция
![]() определена
только при
определена
только при![]() ,
если
,
если![]() —четное число. В
остальном ее свойства подобны свойствам
функции
—четное число. В
остальном ее свойства подобны свойствам
функции![]() .
.
Тригонометрические функции
![]() ,
,![]() непрерывны во всех точках
непрерывны во всех точках![]() .
.
Пример 1.3.Найдите![]() ,
,![]() ,
,![]() .
.
 Решение.Так как функция
Решение.Так как функция![]() непрерывна при
непрерывна при![]() ,
то
,
то![]() .
Поэтому при
.
Поэтому при![]() функция
функция![]() является бесконечно малой (см. 1.4).
является бесконечно малой (см. 1.4).
Из рис. 1.8 видно, что
![]() не существует, так как для любых, сколь
угодно больших или сколь угодно малых
значений аргумента
не существует, так как для любых, сколь
угодно больших или сколь угодно малых
значений аргумента![]() данная функция принимает все значения
из промежутка
данная функция принимает все значения
из промежутка![]() .
.
Аналогичные рассуждения применимы и
для функции
![]() ,
поэтому
,
поэтому![]() не существует.
не существует.
Пример 1.4.Найдите пределы:![]() и
и![]() .
.
Решение. Функция![]() определена и непрерывна во всех точках
вещественной оси кроме точек
определена и непрерывна во всех точках
вещественной оси кроме точек![]() .
Поэтому
.
Поэтому![]() .
.
Функция
![]() определена и непрерывна во всех точках
вещественной оси кроме точек
определена и непрерывна во всех точках
вещественной оси кроме точек![]() .
Значит,
.
Значит,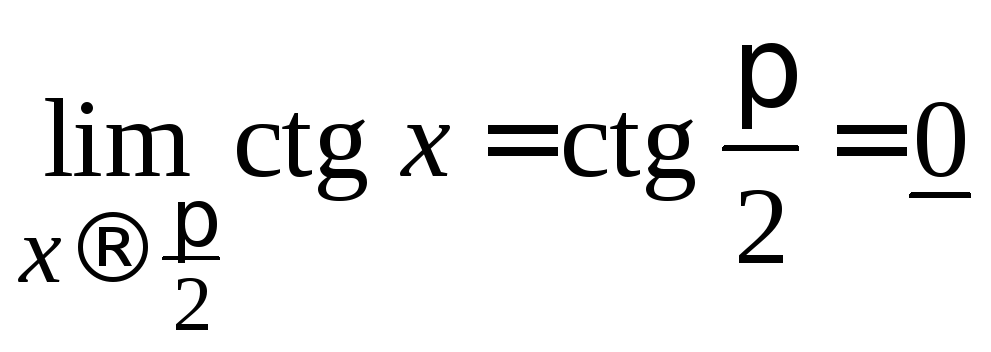 .
.
Пример 1.5.Найдите односторонние
пределы:![]() и
и![]() .
.
Решение. Функция![]() определена и непрерывна во всех точках
вещественной оси, кроме точек
определена и непрерывна во всех точках
вещественной оси, кроме точек![]() .
Из рис. 1.9 видно, что
.
Из рис. 1.9 видно, что![]() ,
а
,
а![]() ,
поэтому в точках разрыва тангенс
является бесконечно большой величиной.
,
поэтому в точках разрыва тангенс
является бесконечно большой величиной.

Функция
![]() терпит разрывы в точках
терпит разрывы в точках![]() .
На графике функции (рис. 1.9)
.
На графике функции (рис. 1.9)![]() видно, что
видно, что![]() и
и![]() .
.
Пример. 1.6.Найдите![]() .
.
Р ешение.Обратная тригонометрическая функция
ешение.Обратная тригонометрическая функция![]() определена и непрерывна для всех
определена и непрерывна для всех![]() .
Все ее значения попадают в промежуток
.
Все ее значения попадают в промежуток .
На графике функции
.
На графике функции![]() (рис. 1.10) видно, что
(рис. 1.10) видно, что![]() ,
,![]() .
.
Построив график функции
![]() можно самостоятельно убедиться в том,
что
можно самостоятельно убедиться в том,
что![]() ,
,![]() .
.
Показательная функция
![]() определена и непрерывна во всех точках
вещественной оси (рис. 1.11).
определена и непрерывна во всех точках
вещественной оси (рис. 1.11).
В зависимости от того, какие значения
принимает основание
![]() ,
показательная функция ведет себя на
бесконечности по-разному. Если
,
показательная функция ведет себя на
бесконечности по-разному. Если![]() ,
то
,
то![]() и
и![]() .
Если
.
Если![]() ,
то
,
то![]() и
и![]() .
.

Пример 1.7.Найдите![]() и
и .
.
Решение.Так как основание
показательной функции равно 3, а 3 > 1,
то![]() .
Напротив, так как
.
Напротив, так как![]() ,
то
,
то .
.
Логарифмическая функция
![]() непрерывна во всех точках
непрерывна во всех точках![]() .
Графики логарифмических функций,
соответствующие различным основаниям,
представлены на рис 1.12.
.
Графики логарифмических функций,
соответствующие различным основаниям,
представлены на рис 1.12.

Е
![]()
![]() ,
то
,
то![]() и
и![]() .
В случае если
.
В случае если![]() ,
то
,
то![]() и
и![]() .
Поскольку логарифмическая функция не
определена при
.
Поскольку логарифмическая функция не
определена при![]() ,
то можно говорить только об одностороннем
пределе справа в точке
,
то можно говорить только об одностороннем
пределе справа в точке![]() (см. 1.5).
(см. 1.5).
