
- •Методы вычисления пределов
- •Предел функции
- •Окрестность точки
- •Предел функции в точке. Непрерывность функции в точке
- •Предел функции на бесконечности
- •Бесконечно большая и бесконечно малая функции
- •Односторонние пределы
- •Элементарные функции
- •Вычисление пределов
- •Правила предельного перехода
- •Предел дробно-рациональной функции
- •Предел функций, содержащих иррациональные выражения
- •Замечательные пределы. Эквивалентные бесконечно малые функции
- •Пределы, содержащие тригонометрические функции
- •Пределы выражений, содержащих показательную, логарифмическую и степенную функции
- •Предел показательно-степенной функции
- •197376, С.-Петербург, Проф. Попова, 5
Вычисление пределов
Правила предельного перехода
Множество
![]() ,
дополненное двумя бесконечно удаленными
точками, называется расширенной числовой
осью и обозначается
,
дополненное двумя бесконечно удаленными
точками, называется расширенной числовой
осью и обозначается![]() .
.![]() .
Арифметические операции над бесконечно
удаленными точками будем осуществлять
по следующим правилам:
.
Арифметические операции над бесконечно
удаленными точками будем осуществлять
по следующим правилам:
1.
![]() ,
,![]() . 4.
. 4.![]() ,
,![]() .
.
2.
![]() . 5.
. 5.![]() ,
,![]() .
.
3.
![]() . 6.
. 6.![]() ,
,![]() .
.
Операции
![]()
![]() не определены.
не определены.
Правила 1 и 4 – 6 определены вне зависимости от знака бесконечности.
Пусть
![]() .
Если при
.
Если при![]() функции
функции![]() и
и![]() имеют конечные или бесконечные пределы,
а
имеют конечные или бесконечные пределы,
а![]() – некоторая постоянная, то
– некоторая постоянная, то
![]()
![]()
![]() (2.2)
(2.2)
![]()
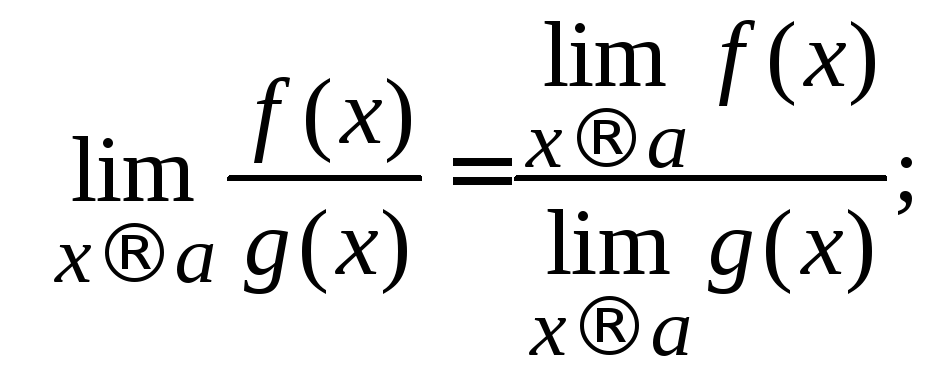 (2.3)
(2.3)
![]() (2.4)
(2.4)
Формула (2.4) вытекает из формулы (2.2),
если в качестве одного из сомножителей
взять постоянную функцию
![]() .
Приведенные формулы известны как
теоремы о пределе суммы, произведения
и частного.
.
Приведенные формулы известны как
теоремы о пределе суммы, произведения
и частного.
Замечание.Операцию деления на ноль
в правиле 6 нужно воспринимать в смысле
предельного перехода, т. е. если![]() и
и![]() ,
но
,
но![]() ,
то
,
то .
.
По формуле (2.3) и в силу правил 5, 6 имеем:
если
![]() и
и![]() ,
то
,
то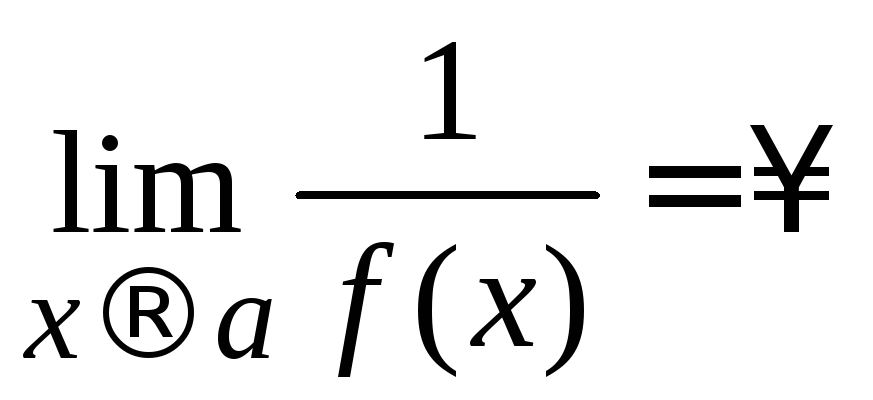 ;
обратно, если
;
обратно, если![]() ,
то
,
то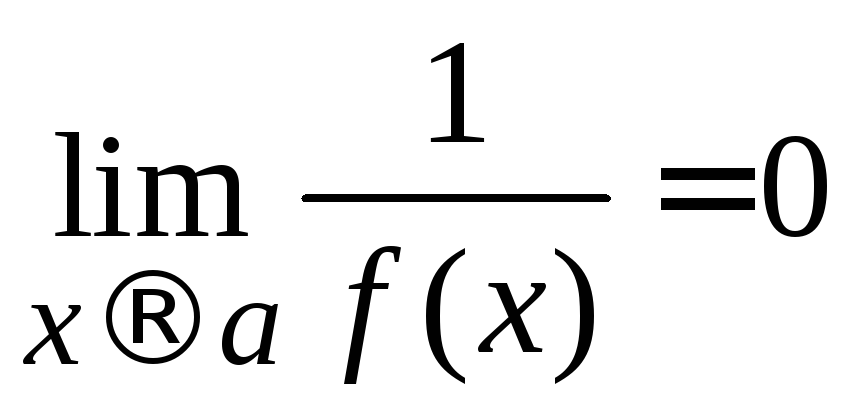 .
Таким образом, функция, обратная к
бесконечно малой, является бесконечно
большой и наоборот, функция, обратная
к бесконечно большой, является бесконечно
малой. Например, так как
.
Таким образом, функция, обратная к
бесконечно малой, является бесконечно
большой и наоборот, функция, обратная
к бесконечно большой, является бесконечно
малой. Например, так как![]() (1.2), то
(1.2), то
 .
(2.5)
.
(2.5)
Рассмотрим композицию функций
![]() [1, 104]. Пусть функция
[1, 104]. Пусть функция![]() имеет конечный или бесконечный предел
при
имеет конечный или бесконечный предел
при![]() ,
т. е.
,
т. е.![]() ,
а функция
,
а функция![]() непрерывна в точке
непрерывна в точке![]() .
Тогда верна формула для предела
композиции функций
.
Тогда верна формула для предела
композиции функций
![]() (2.6)
(2.6)
Пример 2.1. Вычислить![]() .
.
Решение.Воспользуемся формулам (2.1), (2.4) и непрерывностью постоянной и степенной функций (1.1):
![]() =
=
= 3∙16 + 2∙4 – 2 + 1 = 55.
Обобщим полученный результат: предел
многочлена при
![]() равен значению многочлена в точке
равен значению многочлена в точке![]() .
.
Пример 2.2. Вычислить![]() .
.
Решение. По формуле о пределе частного и правилу 5, получаем:
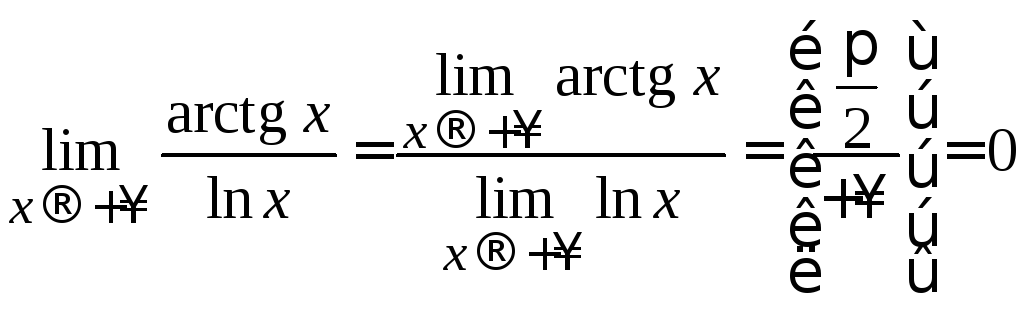 .
.
Пример 2.3. Вычислить![]() ,
,![]() ,
,![]()
![]() .
.
Решение. Для всех слагаемых, за исключением последнего, имеем:
![]() .
Соотношения
.
Соотношения![]() ,
,![]() можно использовать для вычисления
предела многочлена только, если все
слагаемые многочлена стремятся к
бесконечности одного и того же знака.
В общем случае это не так, потому что
знак предела
можно использовать для вычисления
предела многочлена только, если все
слагаемые многочлена стремятся к
бесконечности одного и того же знака.
В общем случае это не так, потому что
знак предела![]() при нечетном
при нечетном![]() определяется не только знаком
определяется не только знаком![]() ,
а зависит еще и от знака
,
а зависит еще и от знака![]() (1.2).
(1.2).
![]() [вынесем
из каждого слагаемого, в качестве общего
множителя, переменную в наивысшей
степени
[вынесем
из каждого слагаемого, в качестве общего
множителя, переменную в наивысшей
степени![]() ]
=
]
=
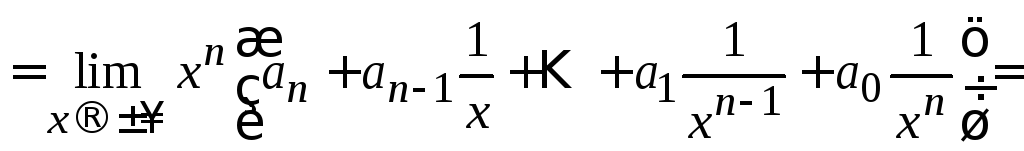
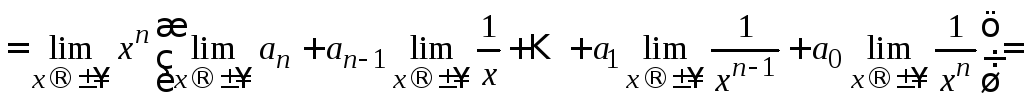 [2.5]=
[2.5]=
![]() [по
правилу 4]=
[по
правилу 4]=![]() .
.
Итак, любой многочлен, степень которого
не меньше 1, является бесконечно большой
функцией при
![]() .
.
Пример 2.4. Вычислить![]() .
.
Решение. Внутренняя показательная
функция![]() является бесконечно малой при
является бесконечно малой при![]() ,
так как ее основание
,
так как ее основание![]() .
Внешняя функция
.
Внешняя функция![]() непрерывна в точке 0. По формуле (2.6)
имеем:
непрерывна в точке 0. По формуле (2.6)
имеем:
![]() .
.
Пример 2.5. Вычислить![]() .
.
Решение. Сначала применим к многочлену, стоящему под корнем, прием, рассмотренный в примере 2.3.
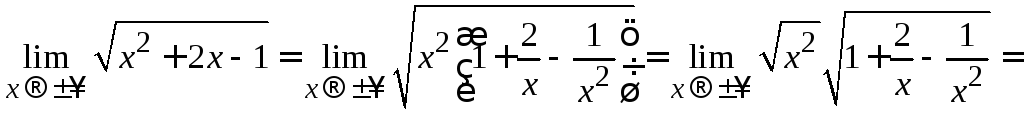 [воспользуемся
формулой о пределе произведения и
учтем, что
[воспользуемся
формулой о пределе произведения и
учтем, что![]() ]
=
]
=
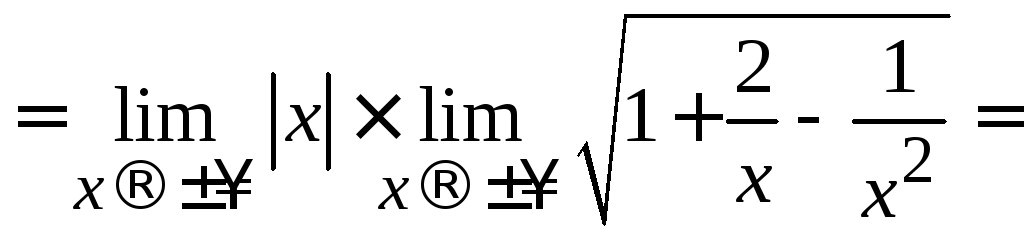 [применим
формулу о пределе композиции функций]
=
[применим
формулу о пределе композиции функций]
=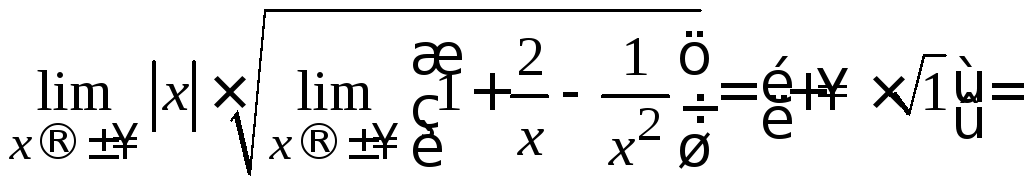
![]() .
.
Рассмотрим предел![]() .
Согласно результату, полученному в
примере 2.5, имеем:
.
Согласно результату, полученному в
примере 2.5, имеем:![]() .
Однако данная операция над бесконечно
удаленными точками не определена. При
столкновении с какой-либо из неопределенных
ситуаций:
.
Однако данная операция над бесконечно
удаленными точками не определена. При
столкновении с какой-либо из неопределенных
ситуаций:
![]() ,
принято говорить, что имеет место
неопределенность соответствующего
типа. Процесс вычисления предела в
случае наличия неопределенности принято
называть «раскрытием неопределенности».
Раскрытию неопределенностей различных
типов будет посвящен следующий раздел,
в котором вернемся к подобному пределу.
,
принято говорить, что имеет место
неопределенность соответствующего
типа. Процесс вычисления предела в
случае наличия неопределенности принято
называть «раскрытием неопределенности».
Раскрытию неопределенностей различных
типов будет посвящен следующий раздел,
в котором вернемся к подобному пределу.
