Замена переменных в двойном интеграле.

Пусть функция непрерывна на замкнутом квадрируемом множествеD, функции ,непрерывны вместе со своими частными производными первого порядка в замкнутом квадрируемом множествеQ и задают взаимно однозначное отображение множества Q на множество D. Тогда имеет место следующая формула замены переменных в двойном интеграле

,

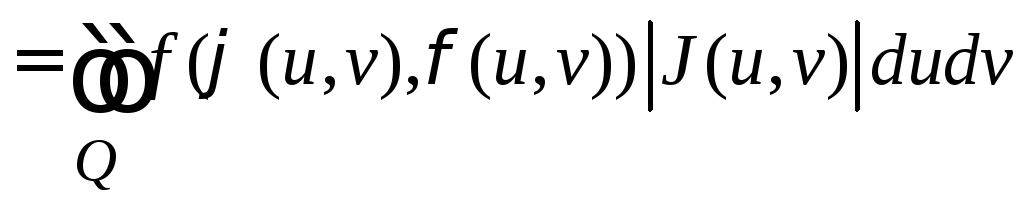где 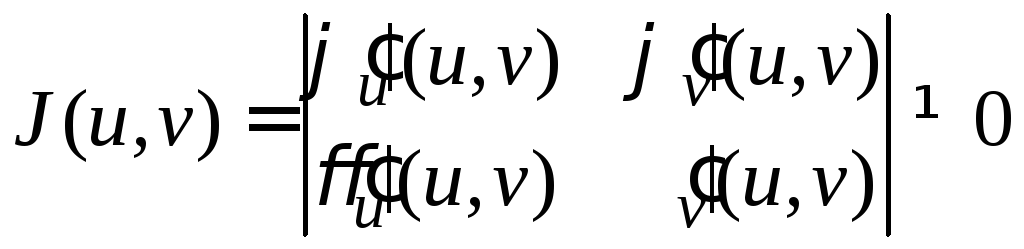. Этот определитель называетсяякобианом отображения ,.

В частности, при переходе к полярной системе координат на плоскости ,якобиан вычисляется следующим образом: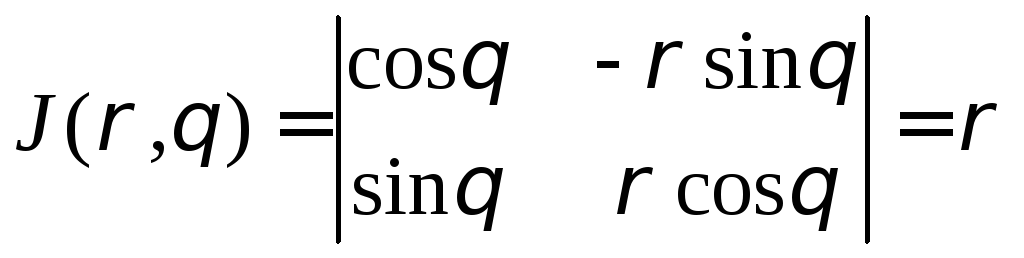, поэтому.

Пример 19. Вычислим интеграл  =, гдеD - круг .

Поскольку границей области интегрирования является окружность

, то при вычислении данного интеграла удобно перейти к полярным координатам ,. При этом отображении прообразом кругаявляется прямоугольник(уравнение окружности в полярной системе координат имеет вид,). Используя формулу замены переменных, получим: =

= =

==.

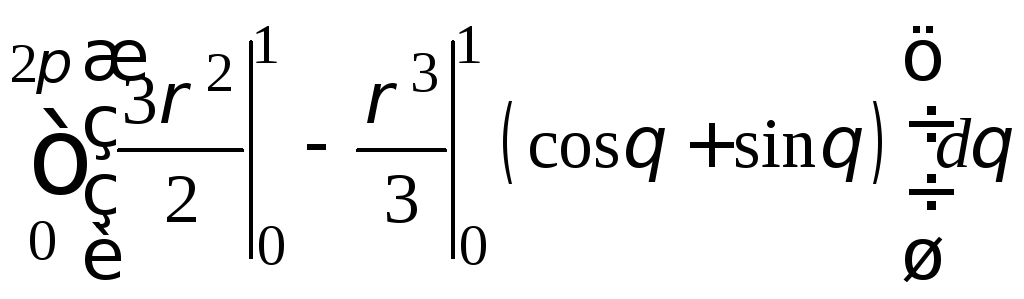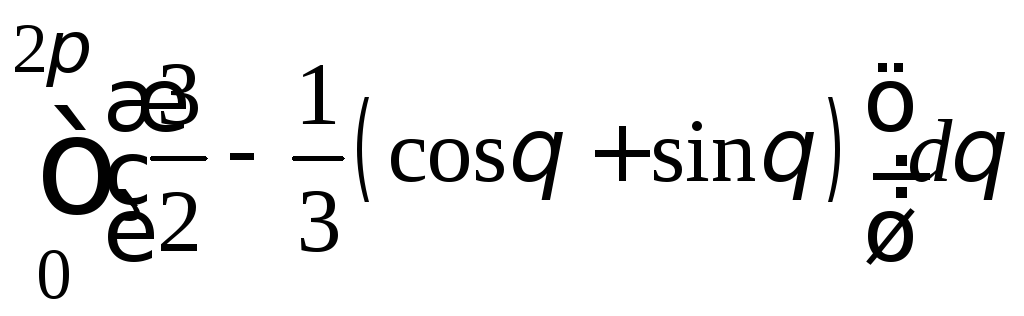ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ

Пусть непрерывная и неотрицательная функция, определенная на замкнутом квадрируемом множествеD.

Объем цилиндрического тела

(криволинейного цилиндра), ограни-

ченного поверхностью ,

плоскостью и прямой цилиндри-

ческой поверхностью, вырезающей на

плоскостимножествоD (рис.9),

вычисляется по формуле:

V =.

Площадь S квадрируемой области Рис.9.

D на плоскости xOy выражается формулой

S =.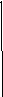

Площадь F гладкой поверхности

, , вычисляется

по формуле

F =

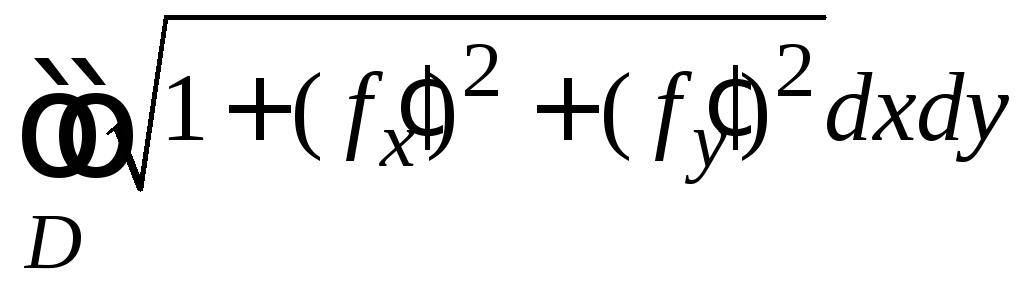
В последней формуле D - проекция данной

Поверхности на плоскость xOy (рис.10). Рис. 10.

Аналогичные формулы имеют место,

если гладкая поверхность задана уравнением ,, (или уравнением,):

F₁ = 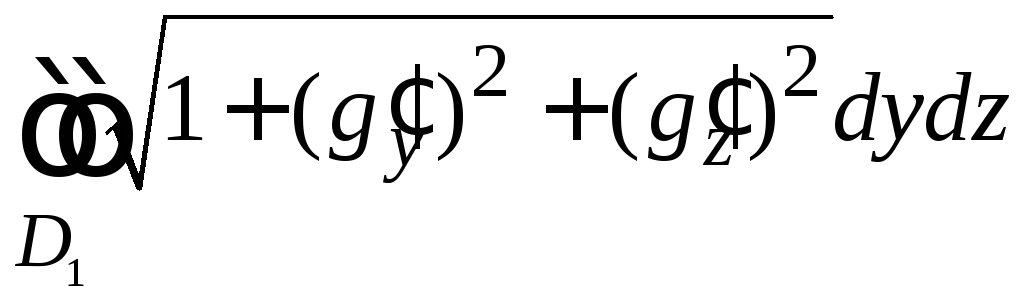(илиF₂ = ).

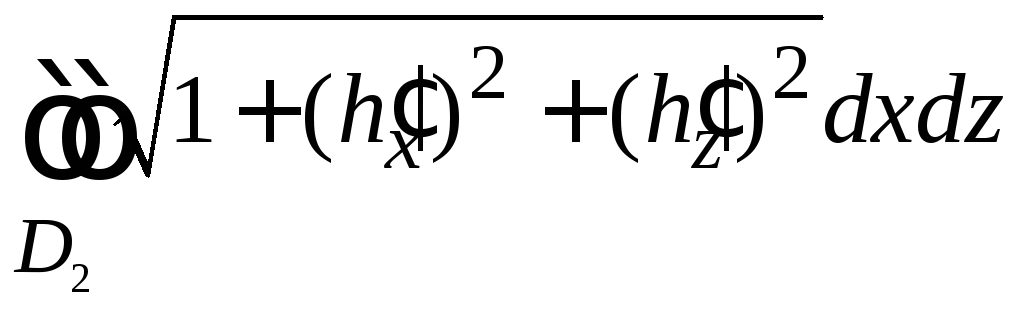Пример 20. Найдем объем тела, ограниченного поверхностью и плоскостями,,и.

Заметим, что уравнение задает цилиндрическую

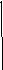z поверхность с образующими,

параллельными оси x, а плоскость

параллельна оси z

(рис. 11).

Область D ограничена прямыми

, и, она может

y быть задана неравенствами ,

.

x Рис. 11 Объем тела V ==

=

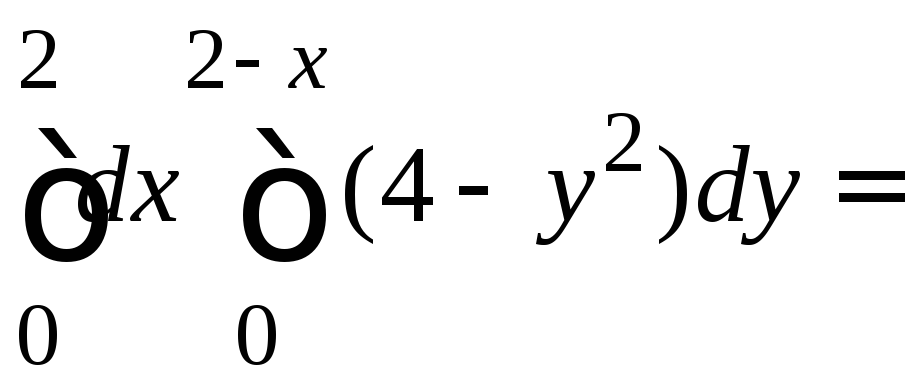
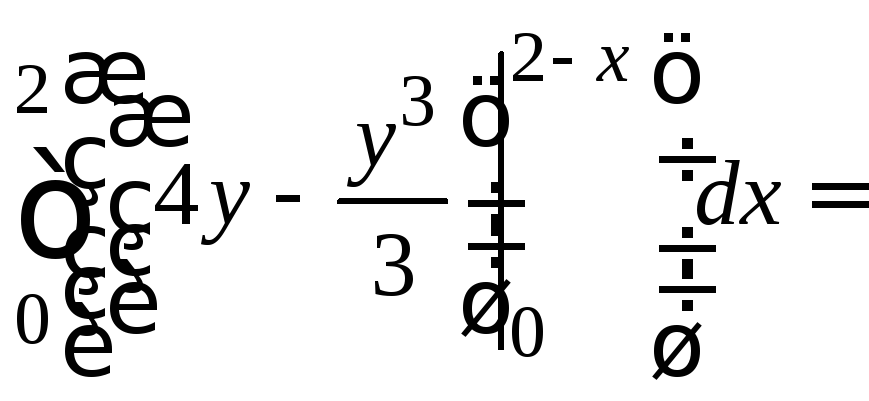
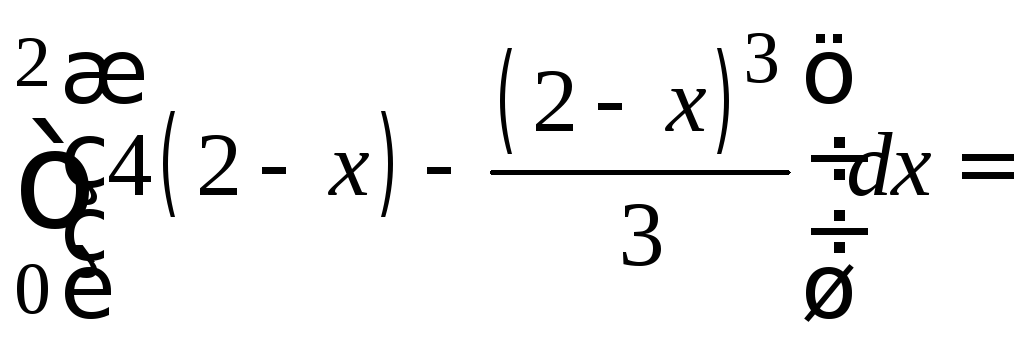
=20/3 (куб.ед.).

Пример 21. Найдем объем тела, ограниченного плоскостями ,и цилиндром.

Тело, объем которого требуетсяz

вычислить, изображено на рис. 12.

Объем тела вычисляется по формуле

V =. Этот интеграл

вычислен в примере 19, он равен 3,

поэтому искомый объем равен

3 (куб.ед.). y

Пример 22. Найдем площадь x

фигуры D, ограниченной кривой Рис. 12

().

Заметим, что кривая симметрична относительно оси x (уравнение кривой не меняется при замене y на -y), расположена в правой полуплоскости (левая часть уравнения неотрицательна, поэтому и правая часть должна быть неотрицательной). Кривая пересекает ось x в точках и.

Кроме того, она ограничена: из очевидного неравенства следует, что, а поскольку, то. Эскиз кривой дан на рис. 13.

Для вычисления площади фигуры D, ограниченной данной кривой,

в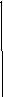оспользуемся формулойS =.

Наличие в формуле кривой двучлена

подсказывает, что целесообразно

перейти к полярным координатам

, .

Полярное уравнение кривой: .

Из условия следует, что меняется

от -/2 до /2, при каждом фиксированном Рис. 13

 переменная  изменяется от 0 до . Используя симметричностьD, мы можем вычислить площадь фигуры, расположенной в первой четверти и удвоить ее. Таким образом,

S== =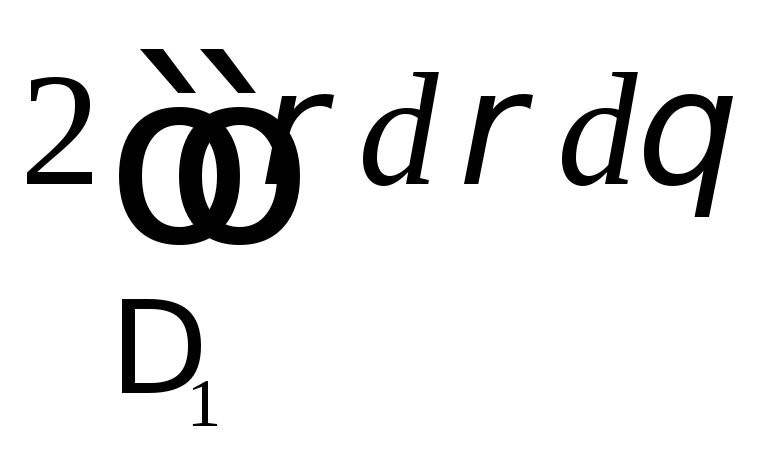

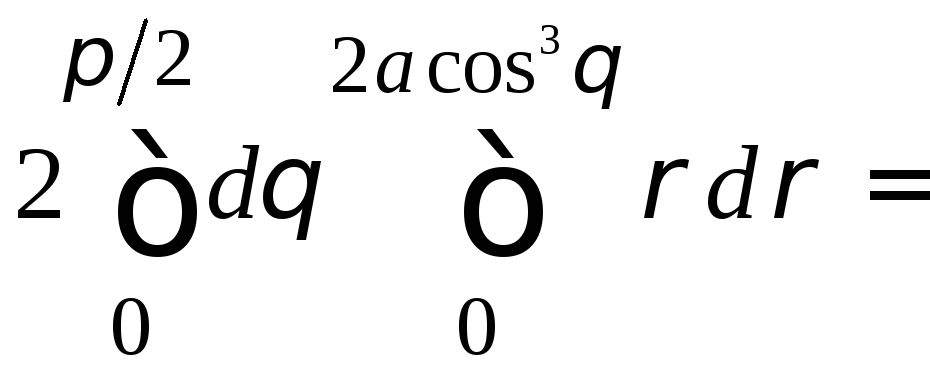
= (кв. ед.).

Пример 23. Вычислим площадь части параболоида , вырезанной цилиндром.

Очевидно, что указанная часть поверхности состоит из четырех равных между собой частей (в силу симметрии параболоида и цилиндра). Поэтому мы можем вычислять площадь одной четвертой части указанной поверхности (например, той, которая находится в первом октанте) и результат умножить на четыре. Таким образом, F=, гдеD - четверть круга , располо-женная в первой четверти., следовательно,,, иF = .

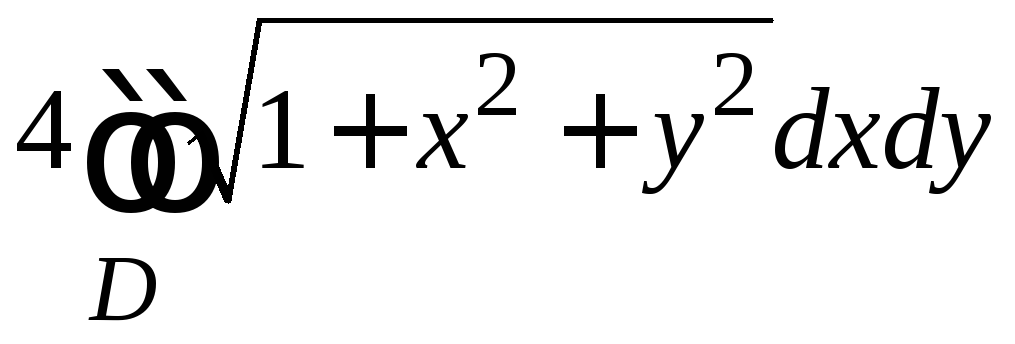Областью интегрирования является часть круга, а подынтегральная функция содержит в себе выражение , поэтому при вычислении интеграла удобно перейти к полярным координатам. ОбластьD в полярных координатах задается неравенствами ,, следовательно,

F ==

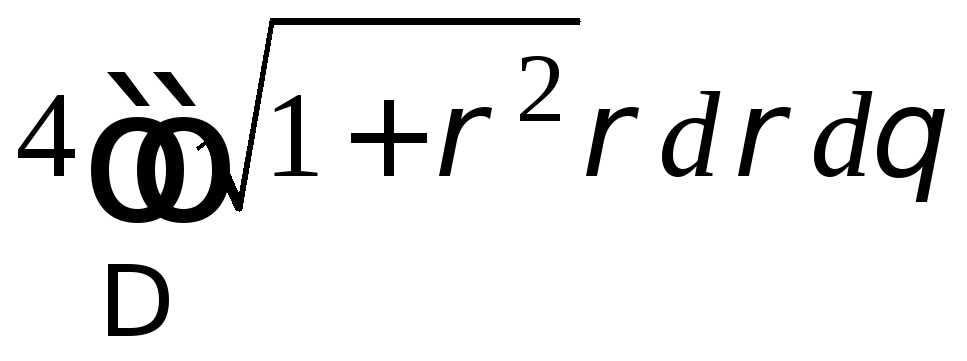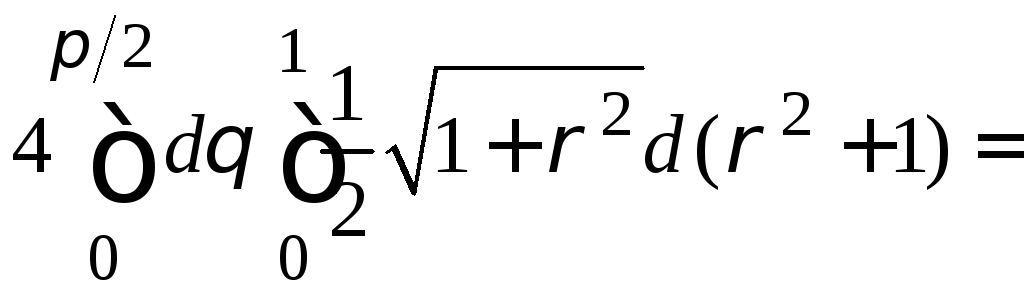
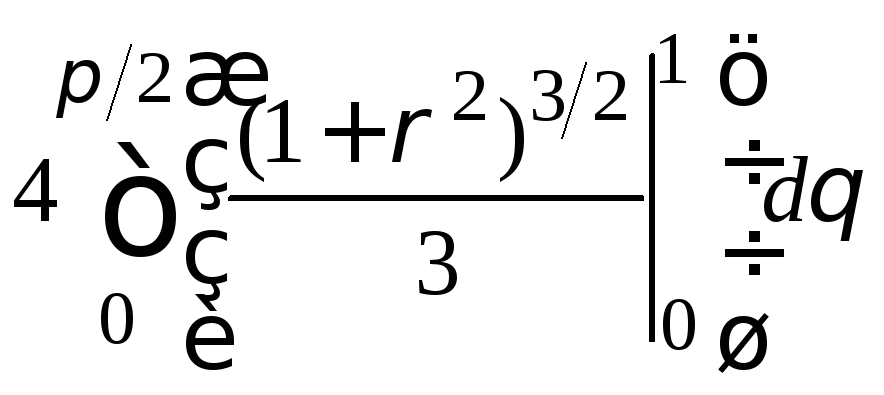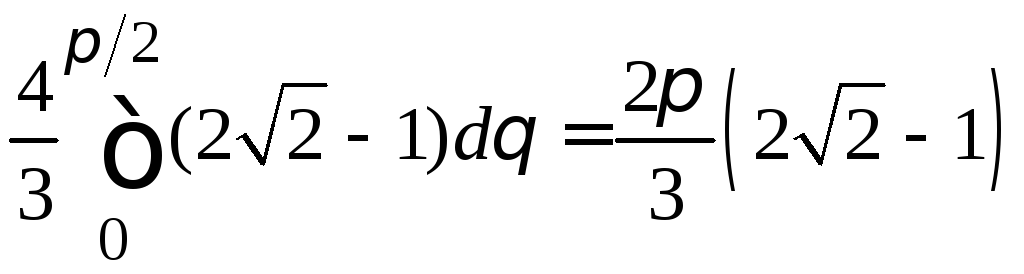= = (кв. ед.).

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

Пусть L - простая спрямляемая незамкнутая кривая, заданная параметрически: ,,.

Напомним, что L называется простой незамкнутой кривой, если функции ,непрерывны наи различным значениям параметраt из отрезка соответствуют различные точки на кривойL. Простая кривая называется спрямляемой, если она имеет конечную длину.

Пусть на кривой L заданы две функции и. Разобьем отрезокнаn частей точками . При этом криваяL разбивается на n частей точками ;- координаты точки.

Введем обозначения: ,,- длина дуги,. На каждой дугевыберем некоторую точку с координатамии составим интегральную сумму

.

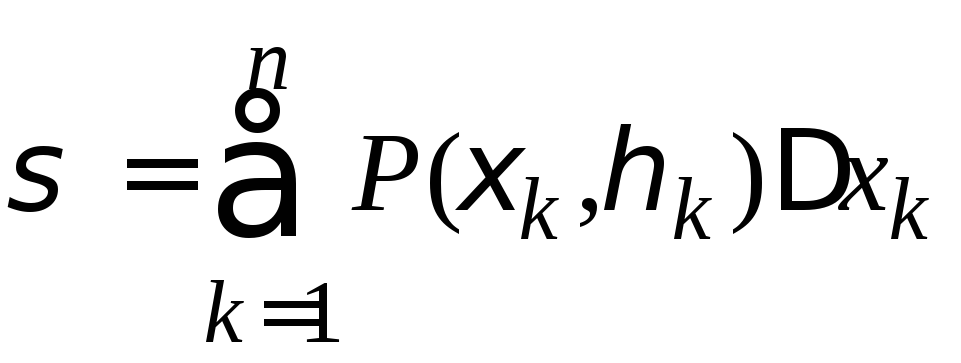
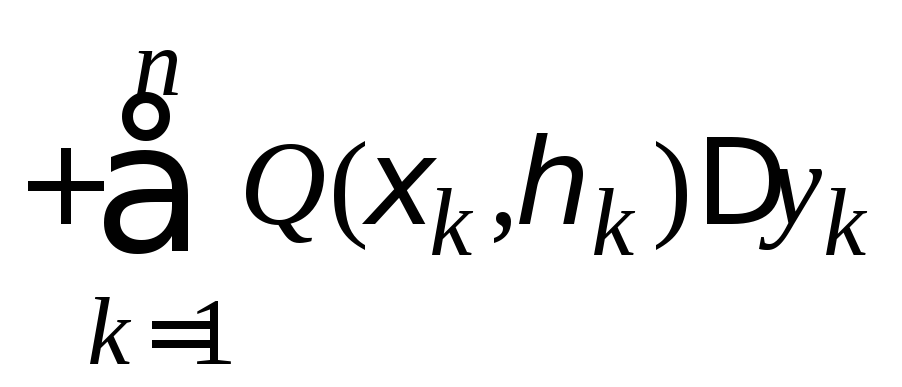Если существует конечный предел , который не зависит ни от способа разбиения отрезкана части, ни от выбора точек, тоJ называется криволинейным интегралом по координатам (криволинейным интегралом второго рода) и обозначается

.

Замечания. 1. Из определения криволинейного интеграла следует, что при изменении направления обхода кривой L изменяется и знак интеграла, т.е. .

2. Если кривая L замкнутая (т.е. точка Aсовпадает с точкойB), то дляL можно указать два направления обхода от A к B. Если область, лежащая внутри контура, остается слева по отношению к движущейся по контуру точке, то такое направление обхода кривой L называется положительным, а противоположное ему - отрицательным.

Интеграл по замкнутому контуру в положительном направлении обозначают так: . Заметим, что в случае вычисления интеграла по замкнутому контуру в качестве начальной (и конечной) точки можно взять любую точку контура.

3. Криволинейные интегралы обладают свойствами линейности и аддитивности.