
- •Функции нескольких переменных. Дифференциальное и интегральное исчисление.
- •Часть 5
- •Функции нескольких переменных
- •Контрольная работа № 8
- •Двойные и криволинейные интегралы и их приложения.
- •Свойства двойных интегралов
- •Вычисление двойных интегралов
- •Замена переменных в двойном интеграле.
- •Вычисление криволинейного интеграла
- •Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •Контрольная работа № 9
Двойные и криволинейные интегралы и их приложения.
ДВОЙНЫЕ ИНТЕГРАЛЫ
Пусть на квадрируемом
множестве
![]() определена функция
определена функция![]() .
.
Под квадрируемым множеством подразумевается такое точечное множество D, которому можно по определенным правилам сопоставить некоторое неотрицательное число, являющееся его площадью.
Разобьем D
произвольными
кривыми на n
частей
![]() .
Пусть
.
Пусть![]() - площади этих частей, а
- площади этих частей, а![]() - их диаметры.
- их диаметры.
Напомним, что диаметром множества называется супремум расстояний между любыми двумя точками, принадлежащими данному множеству.
В каждой из
![]() (
(![]() )
выберем произвольную точку
)
выберем произвольную точку![]() и составиминтегральную
сумму
и составиминтегральную
сумму
 для функции
для функции![]() на множествеD.
на множествеD.
Число
![]() называетсярангом
разбиения D.
называетсярангом
разбиения D.
Если существует
конечный предел
![]() ,
который не зависит ни от способа разбиенияD
на части, ни от выбора точек
,
который не зависит ни от способа разбиенияD
на части, ни от выбора точек
![]() ,
тоJ
называется двойным
интегралом функции
,
тоJ
называется двойным
интегралом функции
![]() по множеству
D
и обозначается
по множеству
D
и обозначается
![]() ;
функция
;
функция![]() в этом случае называетсяинтегрируемой
на множестве
D.
в этом случае называетсяинтегрируемой
на множестве
D.
Заметим, что
функция
![]() ,
непрерывная на замкнутом квадрируемом
множествеD,
интегрируема на D.
,
непрерывная на замкнутом квадрируемом
множествеD,
интегрируема на D.
Свойства двойных интегралов
Пусть функции
![]() и
и![]() интегрируемы на множествеD.
интегрируемы на множествеD.
Линейность интеграла. Для любых постоянных чисел
 и
и функция
функция
![]()
![]() +
+![]()
![]() интегрируема наD
и верно равенство
интегрируема наD
и верно равенство
![]() =
=![]()
![]() +
+![]()
![]() .
.
Аддитивность по множеству. Если D некоторой непрерывной кривой L разбита на два множества D1 и D2 (
 ,
, ),
то функция
),
то функция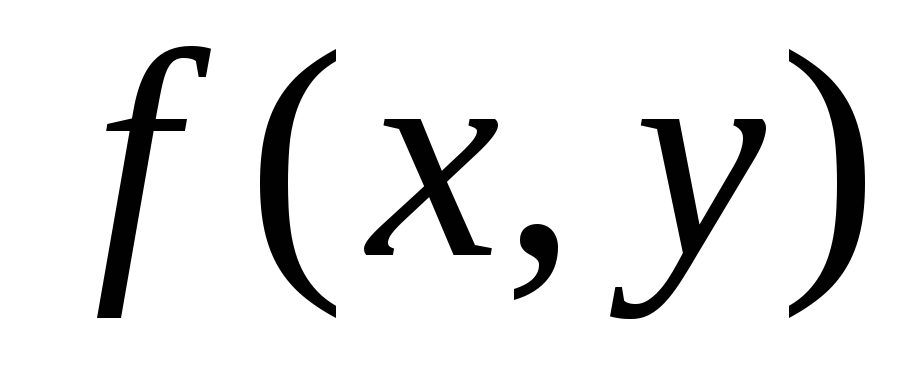 интегрируема наD1
и D2
и
интегрируема наD1
и D2
и
![]() =
= +
+ .
.
Монотонность. Если

 для всех
для всех ,
то
,
то
![]()
![]() .
.
Теорема о среднем значении. Пусть
 определена и непрерывна на связном,
замкнутом и ограниченном множествеD.
определена и непрерывна на связном,
замкнутом и ограниченном множествеD.
Напомним, что множество называется связным, если любые две его точки можно соединить непрерывной кривой, целиком лежащей в этом множестве.
Тогда
существует такая точка
![]() ,
что
,
что
![]()
![]() ,
,
где P - площадь множества D.
Вычисление двойных интегралов
Множество
![]() вида
вида![]() ,
где
,
где![]() - функции, непрерывные наa,b
,
- функции, непрерывные наa,b
,
![]() наa,b,
называется элементарным
относительно
оси y.
наa,b,
называется элементарным
относительно
оси y.
Аналогично,
множество
![]() ,
где
,
где![]() - функции, непрерывные наc,d,
- функции, непрерывные наc,d,
![]() наc,d,
называется элементарным
относительно оси x.
наc,d,
называется элементарным
относительно оси x.
Теорема (о вычислении двойного интеграла повторным интегрированием).
1). Пусть функция
![]() интегрируема на множествеD,
элементарном относительно оси y,
и при каждом постоянном значении x
из a,b
существует интеграл
интегрируема на множествеD,
элементарном относительно оси y,
и при каждом постоянном значении x
из a,b
существует интеграл
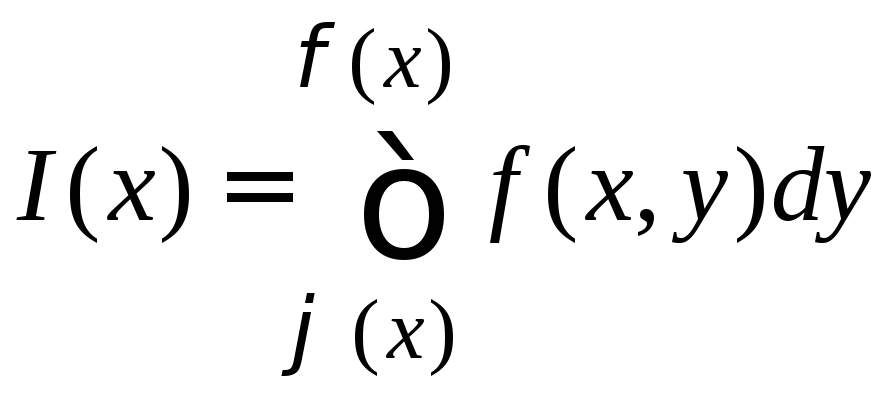 ,
тогда существует также интеграл
,
тогда существует также интеграл ,
который называетсяповторным
,
который называетсяповторным
интегралом,
и выполняется равенство
![]()
 .
.
2). Аналогично, если
функция
![]() интегрируема на множествеD,
элементарном относительно оси x,
и при каждом постоянном значении y
из c,d
существует интеграл
интегрируема на множествеD,
элементарном относительно оси x,
и при каждом постоянном значении y
из c,d
существует интеграл
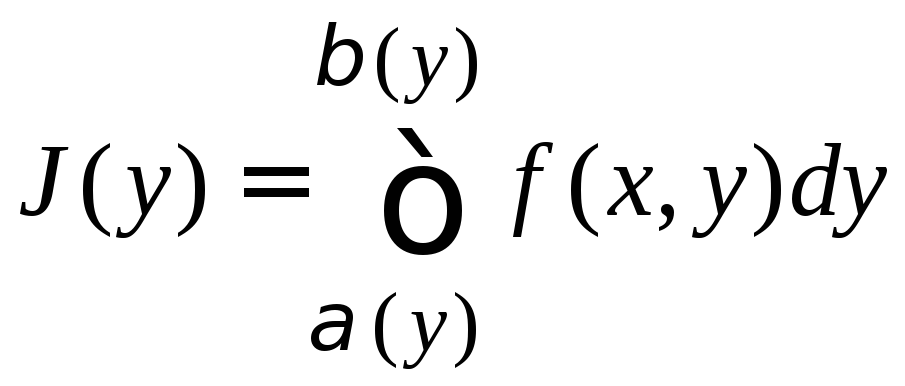 ,
то существует интеграл
,
то существует интеграл ,
и выполняется равенство
,
и выполняется равенство![]()
 .
.
П ример
16. Вычислим
ример
16. Вычислим
 ,
гдеD
- область,
ограниченная кривыми
,
гдеD
- область,
ограниченная кривыми
![]() и
и![]() (рис. 6).
(рис. 6).
Решая систему
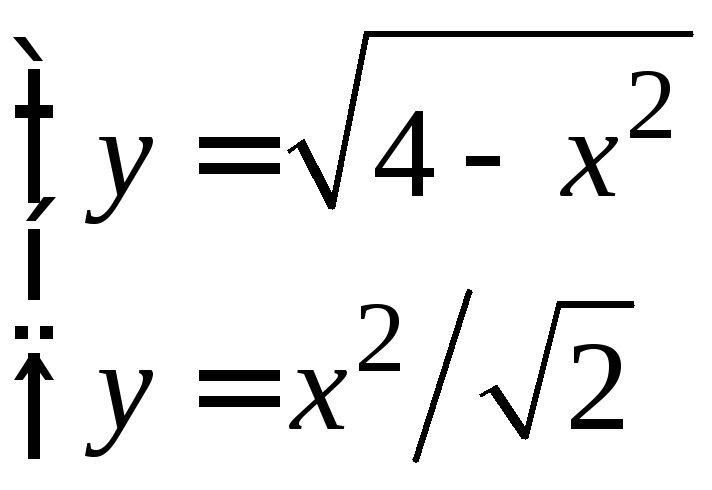 ,
,
найдем абсциссы точек пересечения
п олуокружности
и параболы:
олуокружности
и параболы:![]()
![]() .
Заметим, что множество D
.
Заметим, что множество D
элементарно относительно оси y:
оно задается с помощью неравенств Рис. 6.
![]() ,
,
![]()
![]() .
.
Поэтому двойной интеграл может быть вычислен повторным интегрированием:

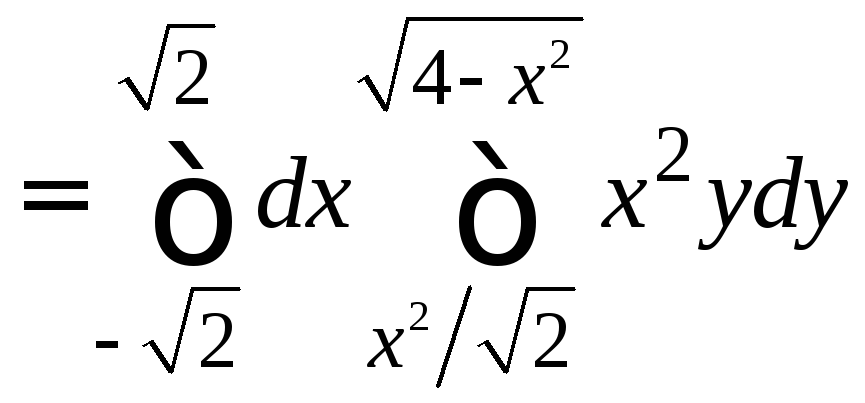 =
=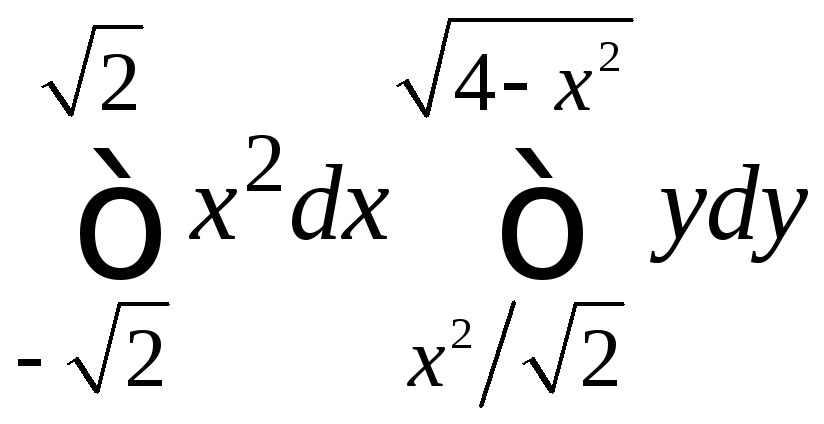
 =
=
 =
=
 .
.
Пример
17. Изменим
порядок интегрирования в повторном
интеграле
 .
.
Эта задача несколько сложнее предыдущей. Здесь не дана непосредственно область интегрирования, мы должны выяснить ее вид по пределам данного повторного интеграла.
Н еравенства
еравенства![]() ,
,![]()
задают множество D, которое изображено
на рис. 7. Проекцией D на ось y является
отрезок
![]() .
Каждая прямаяy=c
.
Каждая прямаяy=c
(c
= const
![]() )
пересекаетD
по отрезку
)
пересекаетD
по отрезку
![]() ,
где
,
где
![]() и
и![]() являются
являются
р ешениями
уравнения
ешениями
уравнения![]() .
.
Решая последнее уравнение, находим
![]() ,
,
![]() .
Рис. 7
.
Рис. 7
Таким образом,
множество D
является элементарным относительно
оси x
и задается неравенствами
![]() ,
,![]() .
Поэтому
.
Поэтому
 =
=![]()
 .
.
Пример 18 .
Изменим порядок интегрирования в
повторном интеграле
.
Изменим порядок интегрирования в
повторном интеграле
 .
y
.
y
Пределы интегрирования в
исходном интеграле показывают,
что область интегрирования D
задается
неравенствами
![]() ,
,
![]() .
Область D
.
Область D
изображена на рис. 8 (кривая
![]()
 является
верхней
x
является
верхней
x
полуокружностью окружности
![]() ).
Легко увидеть,
Рис. 8
).
Легко увидеть,
Рис. 8
что множество D не является
элементарным
относительно оси x,
но его можно разбить на три множества
![]() и
и![]() ,
каждое из которых элементарно
относительно осиx
(см. рис.8).
Разрешая уравнения
,
каждое из которых элементарно
относительно осиx
(см. рис.8).
Разрешая уравнения
![]() и
и![]() относительноx,
получим соответственно
относительноx,
получим соответственно
![]() и
и![]() .
Таким образом, множество
.
Таким образом, множество![]() может быть задано неравенствами
может быть задано неравенствами![]() ,
,![]() ;
множество
;
множество![]() может быть задано неравенствами
может быть задано неравенствами![]() ,
,![]() ;
а множество
;
а множество![]() - неравенствами
- неравенствами![]() ,
,![]() .
Следовательно,
.
Следовательно,

 +
+ +
+ =
=


 .
.
