
- •Функции нескольких переменных. Дифференциальное и интегральное исчисление.
- •Часть 5
- •Функции нескольких переменных
- •Контрольная работа № 8
- •Двойные и криволинейные интегралы и их приложения.
- •Свойства двойных интегралов
- •Вычисление двойных интегралов
- •Замена переменных в двойном интеграле.
- •Вычисление криволинейного интеграла
- •Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •Контрольная работа № 9
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ
УНИВЕРСИТЕТ ИМЕНИ А.И. ГЕРЦЕНА
Функции нескольких переменных. Дифференциальное и интегральное исчисление.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ И
ВАРИАНТЫ КОНТРОЛЬНЫХ ЗАДАНИЙ
для студентов дневного отделения
факультета математики
Часть 5
САНКТ-ПЕТЕРБУРГ
2005
Печатается по решению кафедры математического анализа и РИСа РГПУ им. А.И. Герцена
Методическое пособие предназначено для студентов дневного отделения 1-3 курсов математического факультета РГПУ им. А.И. Герцена.
В соответствии с программой по математическому анализу пособие включает в себя 28 различных вариантов домашних индивидуальных контрольных работ по темам «Дифференциальное исчисление функций нескольких переменных», «Кратные интегралы и их приложения». Перед вариантами контрольных работ приведены некоторые теоретические сведения и разобраны примеры, решение которых сопровождается методическими указаниями к ним.
Материал пособия может быть использован для проведения практических занятий, контрольных и проверочных работ на естественнонаучных факультетах высших учебных заведений.
Авторы-составители: кандидат ф.-м.н., доцент Т.Е. Звягинцева,
Старший преподаватель О.С. Корсакова,
кандидат ф.-м.н., ассистент К.Г. Межевич
Рецензент: зав.каф. матем. анализа РГПУ им. А.И. Герцена,
профессор В.Д. Будаев
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Бохан К.А., Егорова И.А., Лащенов К.В. Курс математического анализа. М.: Просвещение, 1972, т.1,2.
Виленкин Н.Я. и др. Задачник по курсу математического анализа. - М.: Просвещение, 1971. Ч.1,2.
Кузнецов А.А. Сборник заданий по высшей математике. М.: Высшая школа, 1983.
Кудрявцев Л.Д. Курс математического анализа. М.: Высшая школа, 1988. Т. 1,2.
Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу. Функции нескольких переменных. С.-Пб, 1994.
Поволоцкий А.И., Лихтарников Л.М. Метрические пространства. Дифференциальное исчисление функций нескольких переменных. Учебное пособие / ЛГПИ им. А.И. Герцена.-Л., 1985.
Поволоцкий А.И., Лихтарников Л.М. Интегральное исчисление функций нескольких переменных и дифференциальные уравнения. Учебное пособие / ЛГПИ им. А.И. Герцена.-Л., 1986.
Фихтенгольц Г.М. Основы математического анализа. - М.: Наука, 1968. Т.1, 2.
Функции нескольких переменных
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ГРАФИК ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пусть
![]() и каждой точке
и каждой точке![]() поставлено в соответствие число
поставлено в соответствие число![]() .
Тогда говорят, что на множествеD
определена числовая
функция нескольких переменных
.
Тогда говорят, что на множествеD
определена числовая
функция нескольких переменных
![]() .
.
Множество D
называется областью
определения
функции, точка
![]() -аргументом
функции.
-аргументом
функции.
Будем далее
рассматривать функцию двух переменных
![]() .
Отметим, что все сказанное ниже можно
распространить и на функциюn
переменных, где
n>2.
.
Отметим, что все сказанное ниже можно
распространить и на функциюn
переменных, где
n>2.
Множество всех
точек
![]() ,
для которых функция
,
для которых функция![]() ,
заданная аналитически, имеет смысл,
называется естественнойобластью
определения
этой функции.
,
заданная аналитически, имеет смысл,
называется естественнойобластью
определения
этой функции.
Например, областью
определения функции
![]() является открытый круг радиуса 2 с
центром в начале координат, который
задается неравенством
является открытый круг радиуса 2 с
центром в начале координат, который
задается неравенством![]() .
.
Графиком
функции
![]() ,
где
,
где![]() ,
называется множество
,
называется множество![]() .
Оно задает некоторую поверхность в
пространстве
.
Оно задает некоторую поверхность в
пространстве![]() .
.
Например, графиком
функции
![]() ,
,![]() ,
является параболоид.
,
является параболоид.
Пример
1. Найдем
область определения функции
![]() .
.
Функция
![]() определена в тех точках плоскости
определена в тех точках плоскости![]() ,
где
,
где![]() .
.
Это неравенство равносильно совокупности двух систем:
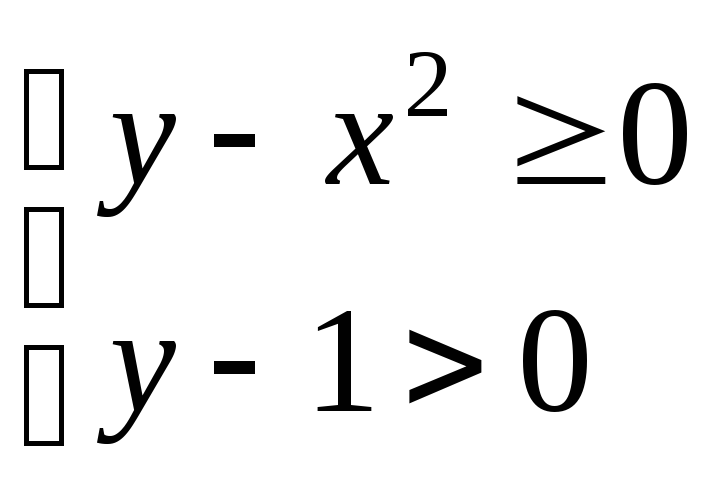 и
и
 .
.
Первой системе
неравенств удовлетворяют координаты
всех точек, расположенных на параболе
![]() или выше нее, и лежащих в полуплоскости
или выше нее, и лежащих в полуплоскости![]() .
Это множество заштриховано на рисунке
1. Второй системе удовлетворяют
координаты точек, лежащих в множестве,
заштрихованном на рис. 2. Следовательно,
областью определения данной функции
является объединение найденных множеств,
т.е. множество, которое выделено штриховкой
на рис. 3.
.
Это множество заштриховано на рисунке
1. Второй системе удовлетворяют
координаты точек, лежащих в множестве,
заштрихованном на рис. 2. Следовательно,
областью определения данной функции
является объединение найденных множеств,
т.е. множество, которое выделено штриховкой
на рис. 3.
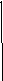
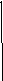
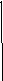 y
y
y
y
y
y


 x
x
x
x
x
x
Рис. 1 Рис. 2 Рис. 3
Линией уровня
функции
![]() ,
называется множество точек
,
называется множество точек![]() ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению![]() .
.
Аналогично определяются уровни (или поверхности уровня) функции n переменных, если n>2.
Пример
2. Найдем
линии уровня функции
![]() .
.
Отметим, что
функция определена на всей плоскости
![]() .
.
Для построения
линий уровня надо для любого
![]() найти множество точек плоскости,
координатыx,
y
которых
удовлетворяют уравнению
найти множество точек плоскости,
координатыx,
y
которых
удовлетворяют уравнению
![]() .
Следовательно, если
.
Следовательно, если![]() ,
то
,
то![]() ,
а если
,
а если![]() ,
то
,
то![]() .
.
Очевидно, что с отрицательным быть не может (в этом случае говорят, что с-уровнем функции при c<0 является пустое множество).
Найдем линию уровня при с=0:
![]()
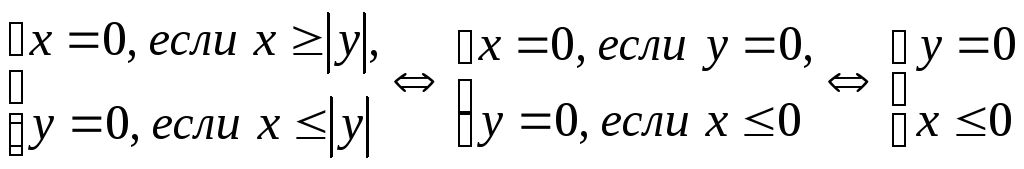 .
.
Аналогично находятся линии уровня для различных с>0.
На рис. 4 изображены линии уровня для с=0, с=1 и с=2.
 y
y

 c=2
c=2
c=1



 . c=0
x
. c=0
x


Рис.4
ПРЕДЕЛ ФУНКЦИИ
Множество
![]() (открытый круг радиуса
(открытый круг радиуса![]()
![]() с центром в точке
с центром в точке![]() )
называется
)
называется![]() -окрестностью
точки
-окрестностью
точки
![]() .
Через
.
Через![]() будем обозначать проколотую окрестность
точки
будем обозначать проколотую окрестность
точки![]() .
.
Точка
![]() называетсяпредельной
точкой
множества
называетсяпредельной
точкой
множества
![]() ,
если пересечение любой
,
если пересечение любой![]() -окрестности
точки
-окрестности
точки![]() и множестваD
содержит хотя бы одну точку, отличную
от
и множестваD
содержит хотя бы одну точку, отличную
от
![]() ,
т.е. для
,
т.е. для![]()
![]() .
.
Заметим, что предельная точка может и не принадлежать множеству D.
Пусть функция
![]() определена на множествеD
и точка
определена на множествеD
и точка
![]() - предельная точкаD.
- предельная точкаD.
Число А
называется пределом
функции
![]() в точке
в точке![]() ,
если для любой
,
если для любой![]() -окрестности
-окрестности![]() точкиА
(
точкиА
(![]() )
существует
)
существует![]() -окрестность
-окрестность![]() точки
точки![]() такая, что для любой точки
такая, что для любой точки![]()
![]() значение функции
значение функции![]() попадает в окрестность
попадает в окрестность![]() .
.
Таким образом,
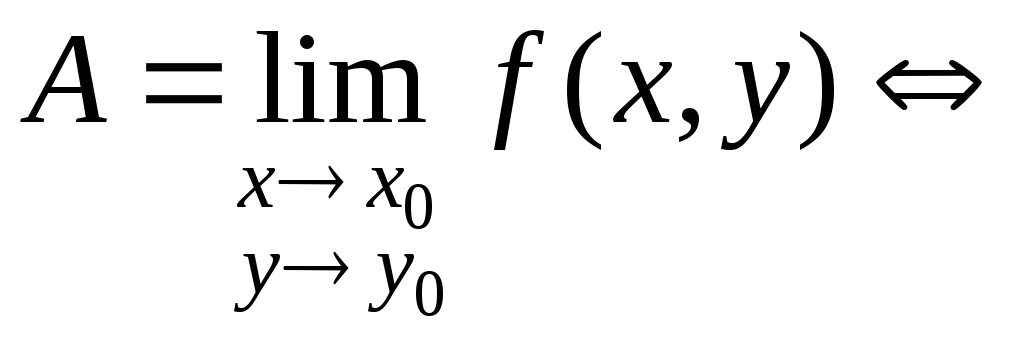
![]()
![]() :
:
![]()
![]()
![]()
![]() )
)![]()
![]()
![]() :
:
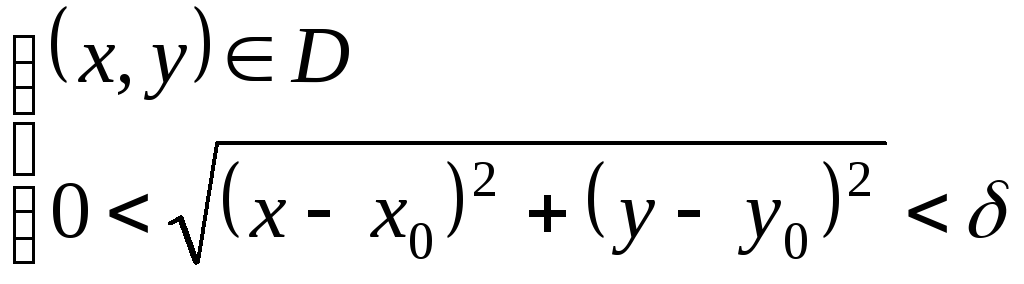
![]() ).
).
Пример
3. Докажем,
что
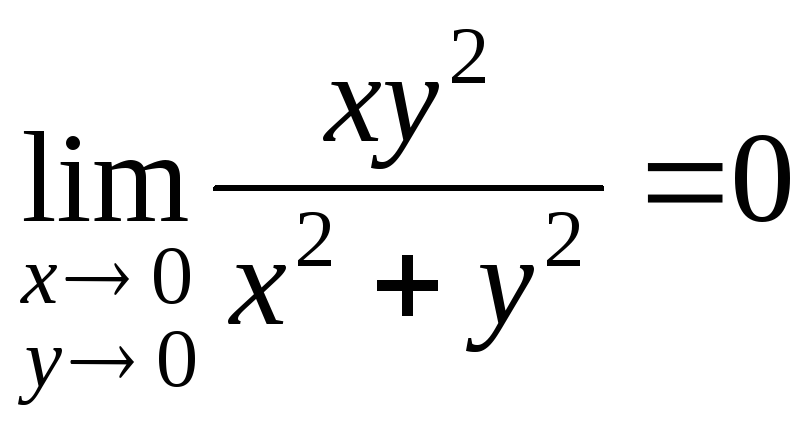 .
.
Заметим, что данная
функция определена на всей плоскости
![]() за исключением точки (0,0).
за исключением точки (0,0).
Поскольку
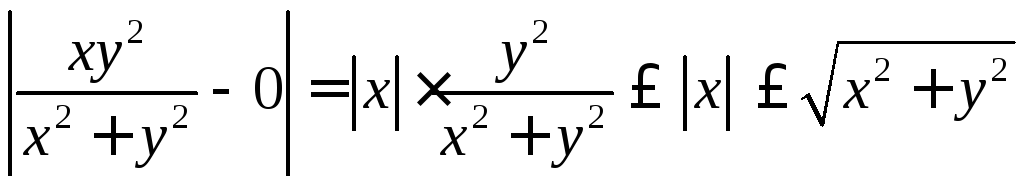 ,
то для любого
,
то для любого![]() существует
существует![]() (а именно
(а именно![]() )
такое, что для всех точек
)
такое, что для всех точек![]() ,
удовлетворяющих условию
,
удовлетворяющих условию![]() ,
справедливо неравенство
,
справедливо неравенство![]() .
.
Функция
![]() называетсянепрерывной
в точке
называетсянепрерывной
в точке
![]() ,
если
,
если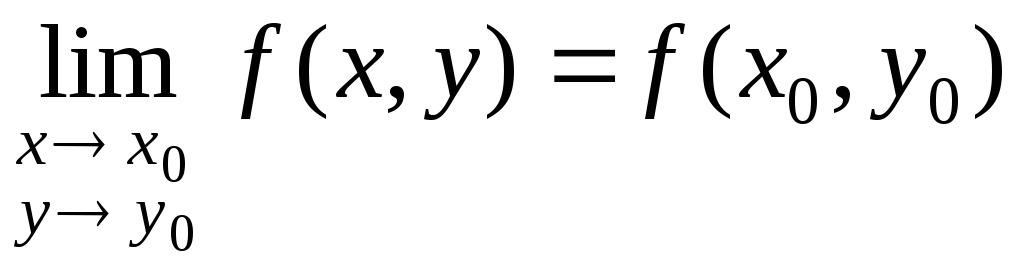 .
.
Функция называется непрерывной на множестве D, если она непрерывна в каждой точке множества D.
Пример
4. 1) Функция
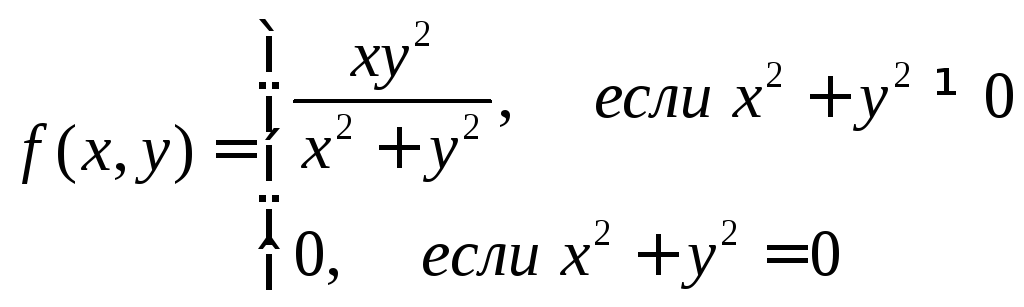 непрерывна в точке (0,0), поскольку
непрерывна в точке (0,0), поскольку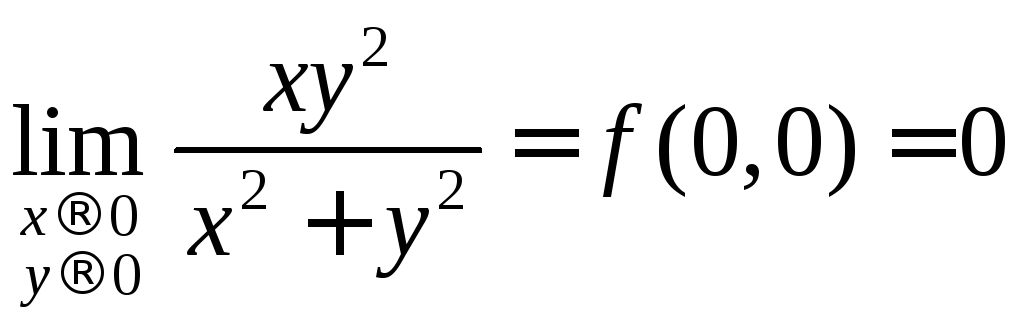 (см. пример 3).
(см. пример 3).
2) Функция
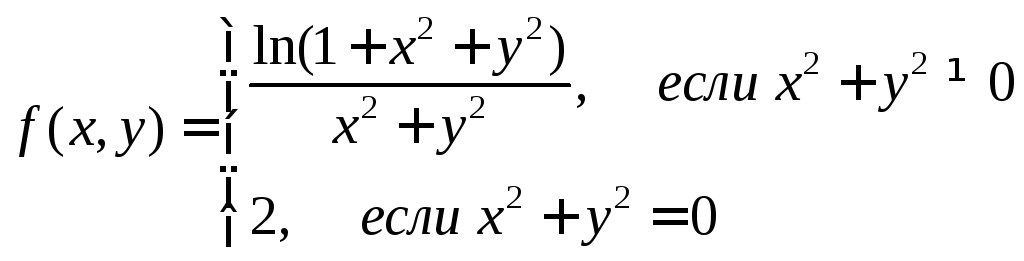 в точке (0,0) терпит разрыв, т.к.
в точке (0,0) терпит разрыв, т.к.
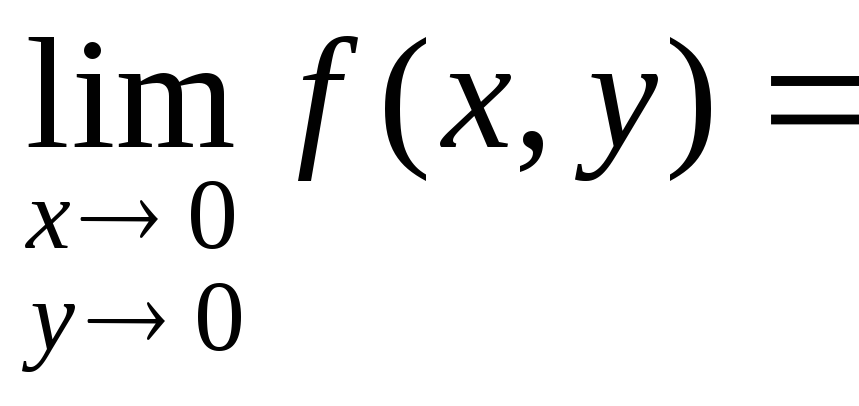
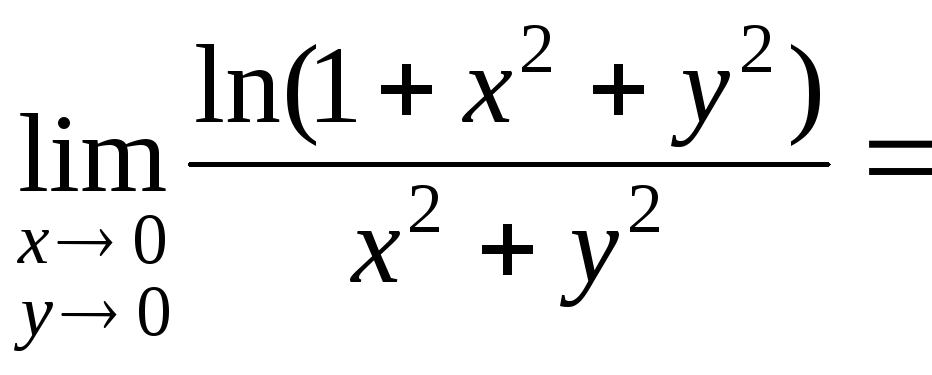
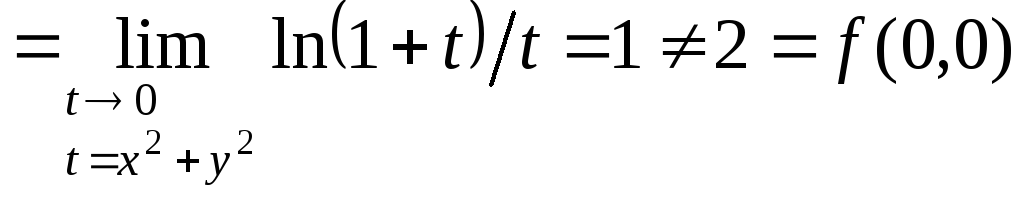 .
.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() .
Если существуют конечные пределы
.
Если существуют конечные пределы![]() и
и![]() ,
то они называютсячастными
производными
функции
,
то они называютсячастными
производными
функции
![]() в точке
в точке![]() по переменнымx
и
y
соответственно и обозначаются
по переменнымx
и
y
соответственно и обозначаются
![]() и
и![]() (или:
(или:![]() и
и![]() ).
).
Для вычисления
частной производной
![]() (или
(или![]() )
пользуются известными формулами и
правилами дифференцирования функции
одной переменной, считая другую переменнуюy
(или x)
постоянной величиной.
)
пользуются известными формулами и
правилами дифференцирования функции
одной переменной, считая другую переменнуюy
(или x)
постоянной величиной.
Пример 5.
Найдем частные производные функции
![]() .
.
Если считать
y=const,
то
![]() - степенная функция отx
, поэтому
- степенная функция отx
, поэтому
![]() .
.
Если x=const,
то
![]() - показательная функция отy,
и, следовательно,
- показательная функция отy,
и, следовательно,
![]() .
.
Функция
![]() называетсядифференцируемой
в точке
называетсядифференцируемой
в точке
![]() ,
если существуют числаА
и В
такие, что приращение
,
если существуют числаА
и В
такие, что приращение
![]()
![]()
![]() функцииf
в точке
функцииf
в точке
![]() представимо в виде
представимо в виде
![]() ,
,
где
![]() при
при![]() .
.
Главная часть
полного приращения
![]() ,
линейная относительно
,
линейная относительно![]() и
и![]() ,
т.е.
,
т.е.![]() ,
называетсяполным
дифференциалом
функции
,
называетсяполным
дифференциалом
функции
![]() в точке
в точке![]() и обозначается
и обозначается![]() .
.
Таким образом,
![]()
![]() .
.
Дифференциалом
независимой переменной по определению
считаем ее приращение, т.е.
![]() ,
,![]() .
.
Функция называется дифференцируемой на множестве D, если она дифференцируема в каждой точке множества D.
Теорема 1.
Если функция
![]() дифференцируема в точке
дифференцируема в точке![]() и
и![]()
![]() - ее дифференциал в этой точке, то в этой
точке существуют частные производные
функцииf,
и, кроме
того,
- ее дифференциал в этой точке, то в этой
точке существуют частные производные
функцииf,
и, кроме
того,
![]() =А,
=А,
![]() =В.
=В.
Теорема 1 дает возможность вычислять дифференциал функции f по формуле
![]()
![]() +
+
![]() .
.
Согласно теореме 1, если функция дифференцируема в точке, то в этой точке существуют частные производные функции. Обратное не верно. Для дифференцируемости функции требуется выполнение более сильных условий, чем наличие частных производных в точке.
Теорема 2.
Если частные производные
![]() и
и![]() функцииf
существуют в некоторой окрестности
точки
функцииf
существуют в некоторой окрестности
точки
![]() и непрерывны в
и непрерывны в![]() ,
то функцияf
дифференцируема
в точке
,
то функцияf
дифференцируема
в точке
![]() .
.
Пример 6.
Вычислим частные производные и
дифференциал функции
![]() в точке (1, 1/5).
в точке (1, 1/5).
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ;
;
![]() .
.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ СЛОЖНОЙ ФУНКЦИИ
Теорема 3.
Пусть функции
![]() и
и![]() определены в некоторой окрестности
точки
определены в некоторой окрестности
точки![]() ,
а функция
,
а функция![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() .
.
Если функция f
дифференцируема
в точке
![]() ,
а в точке
,
а в точке![]() существуют производные
существуют производные![]() ,
то в точке
,
то в точке![]() существует производная сложной функции
существует производная сложной функции![]() ,
причем
,
причем
![]() ,
,
![]() .
.
Пример
7. Найдем
частные производные сложной функции
![]() ,
где
,
где![]() ,
,![]() .
.
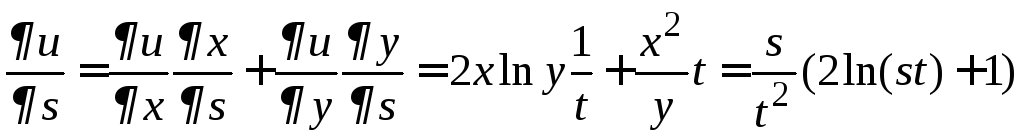 ,
,
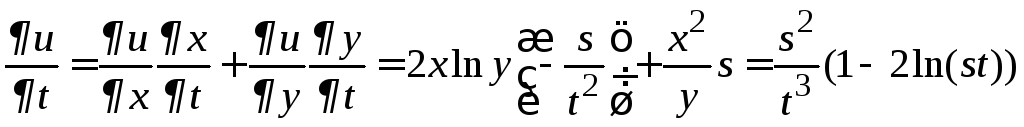 .
.
Пример 8.
Найдем производную сложной функции
![]() ,
где
,
где![]() ,
,![]() .
В этом примере функцииx
и y
зависят от
одной переменной t,
поэтому сложная функция
.
В этом примере функцииx
и y
зависят от
одной переменной t,
поэтому сложная функция
![]() -
функция одной переменной.
-
функция одной переменной.
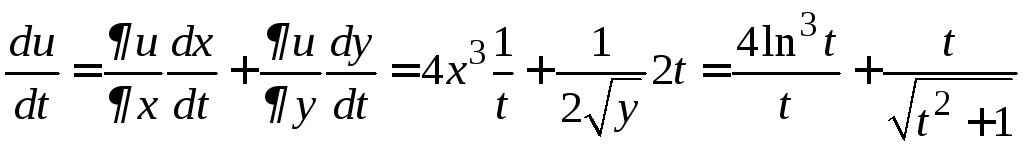 .
.
Пример 9. Пусть
f(u)
- произвольная дифференцируемая функция.
Докажем, что функция
![]() удовлетворяет уравнению
удовлетворяет уравнению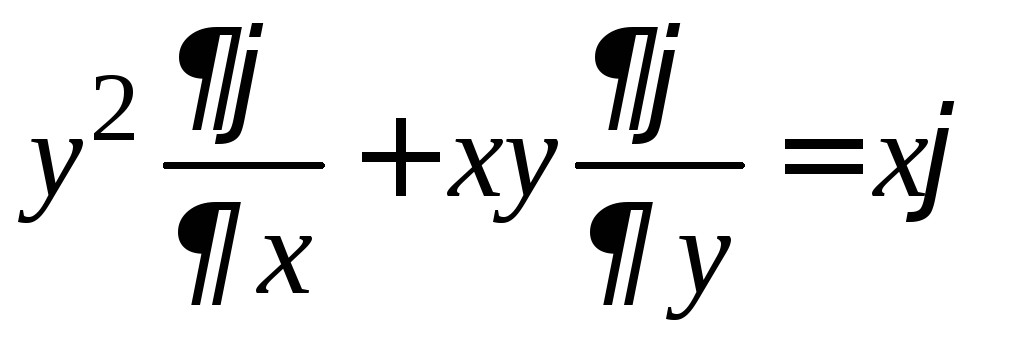 .
Положим
.
Положим![]() .
.
Тогда
![]() .
.
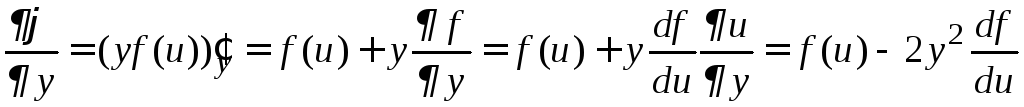 .
.
Следовательно,
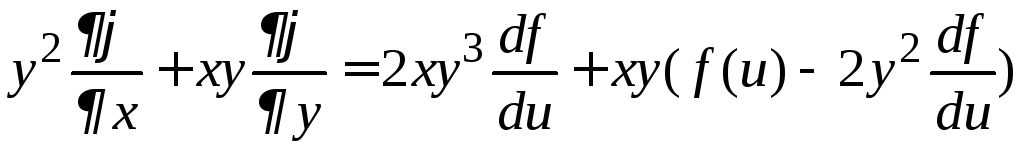
![]() .
.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
ВЫСШИХ ПОРЯДКОВ
Пусть функция
![]() в окрестности точки
в окрестности точки![]() имеет частную производную
имеет частную производную![]() .
.
Частная производная
функции
![]() по переменнойx
называется
частной
производной
второго
порядка по
переменной x
и обозначается
по переменнойx
называется
частной
производной
второго
порядка по
переменной x
и обозначается
![]() или
или![]() .
.
Частная производная
![]() по переменной
y
называется частной
производной
второго
порядка по
переменным x
и y
и обозначается
по переменной
y
называется частной
производной
второго
порядка по
переменным x
и y
и обозначается
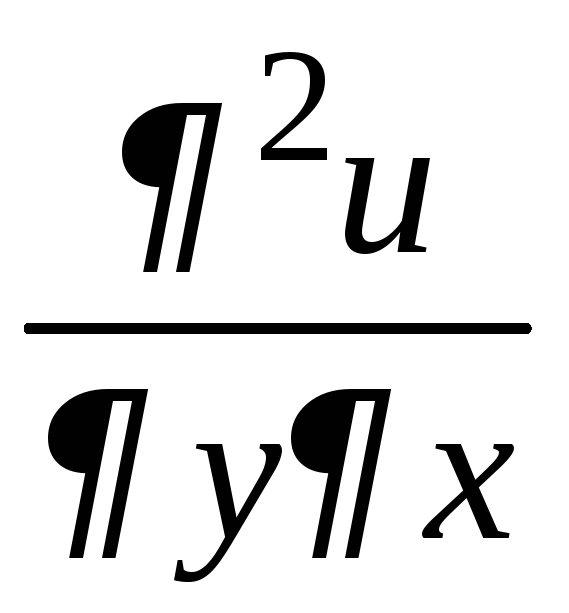 или
или
![]() .
.
Аналогично
определяются частные производные
второго порядка
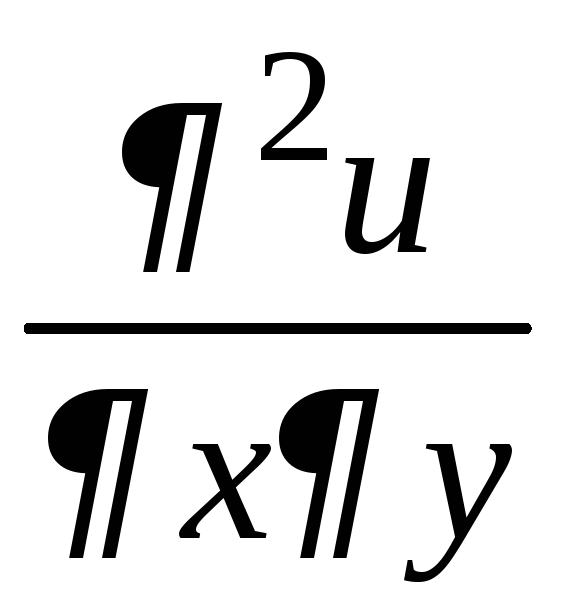 и
и![]() (
(![]() и
и![]() )
как частные производные функции
)
как частные производные функции![]() .
.
Производные
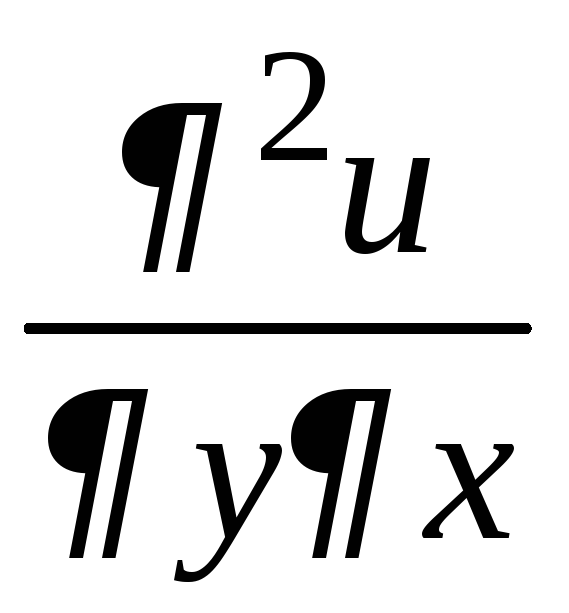 и
и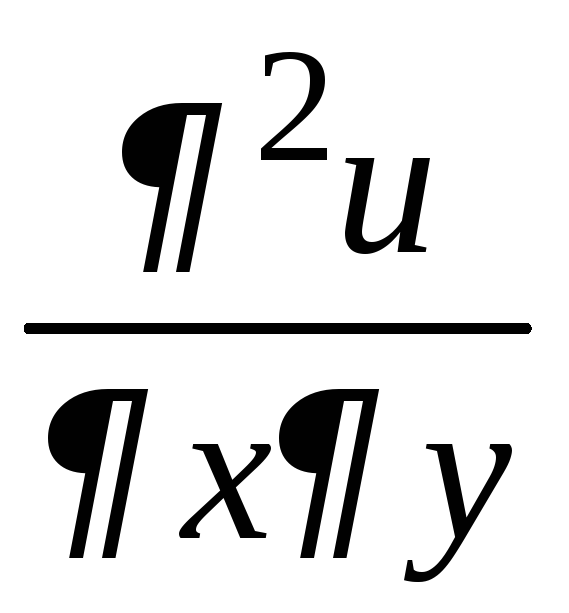 называютсясмешанными
частными производными.
называютсясмешанными
частными производными.
Теорема
4. Пусть
функция
![]() определена вместе со своими частными
производными
определена вместе со своими частными
производными![]() ,
,![]() ,
,![]() ,
,![]() в некоторой окрестности точки
в некоторой окрестности точки![]() ,
причем смешанные производные
,
причем смешанные производные![]() и
и![]() непрерывны в этой точке. Тогда значения
смешанных производных в этой точке
равны, т.е.
непрерывны в этой точке. Тогда значения
смешанных производных в этой точке
равны, т.е.![]()
![]() =
=![]()
![]() .
.
Частные производные
от производных второго порядка называются
частными производными третьего порядка:
 и т.д.
и т.д.
Частная производная (по любой из независимых переменных) от частной производной порядка m-1 называется частной производной порядка m.
Теорема 4 справедлива
и для смешанных производных третьего,
четвертого и более высоких порядков.
Например, если функция
![]() определена вместе со своими частными
производными до порядка 3 включительно
в некоторой окрестности точки
определена вместе со своими частными
производными до порядка 3 включительно
в некоторой окрестности точки![]() ,
причем смешанные производные
,
причем смешанные производные![]() ,
,![]() и
и![]() непрерывны в этой точке, то значения
смешанных производных в этой точке
равны:
непрерывны в этой точке, то значения
смешанных производных в этой точке
равны:![]()
![]() =
=![]()
![]() =
=![]()
![]() .
.
Дифференциалом второго порядка функции двух переменных называется дифференциал от дифференциала первого порядка.
Если функция
![]() дважды непрерывно дифференцируема в
некоторой окрестности точки
дважды непрерывно дифференцируема в
некоторой окрестности точки![]() (т.е. существуют непрерывные частные
производные функцииf
до второго
порядка включительно в окрестности
точки
(т.е. существуют непрерывные частные
производные функцииf
до второго
порядка включительно в окрестности
точки
![]() ),
тогда
),
тогда
![]()
![]()
![]() .
.
Пример 10.
Найдем производные второго порядка
дважды непрерывно дифференцируемой
сложной функции
![]() ,
где
,
где![]() ,
,![]() .
.
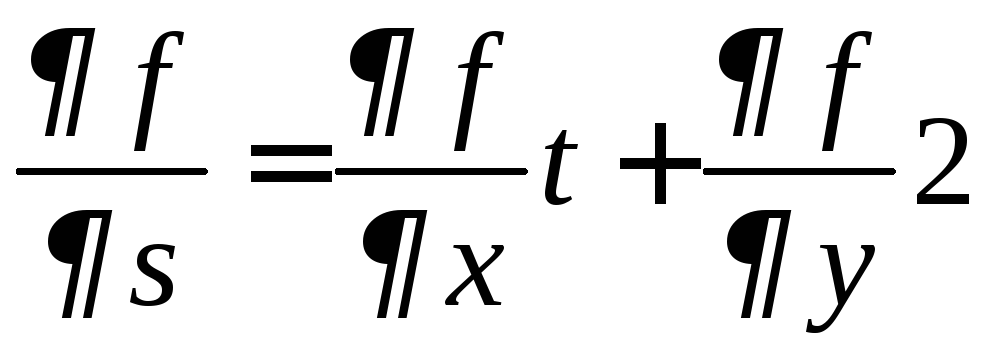 ,
,
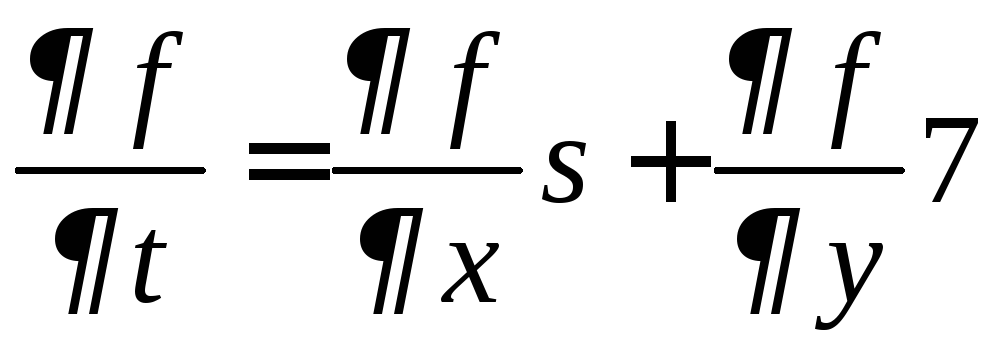 .
.
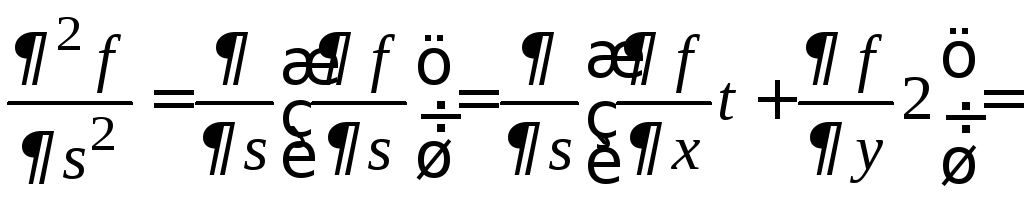
 =
=
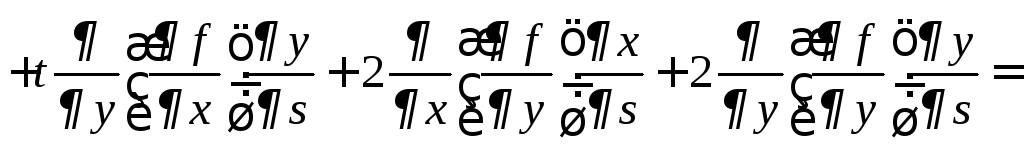
=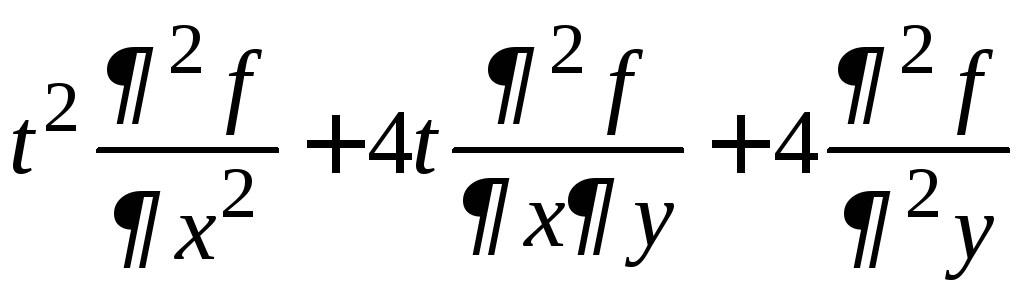 ,
,

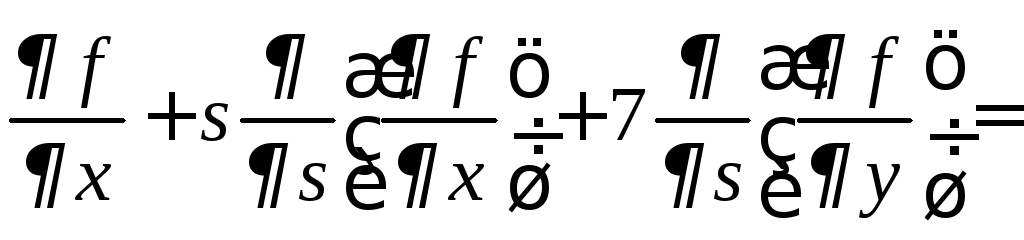 =
=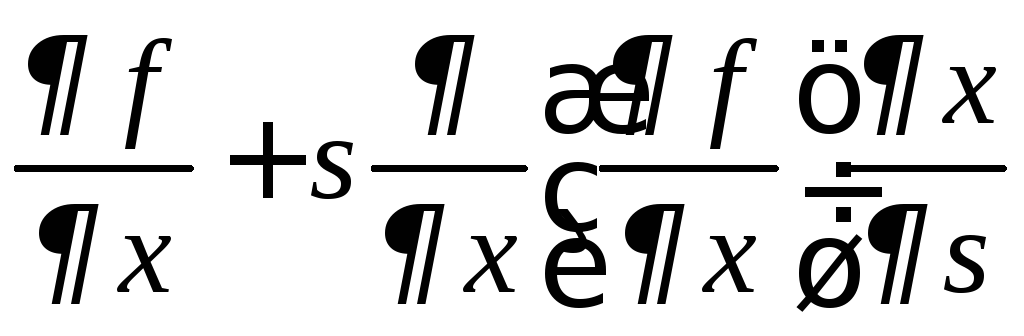
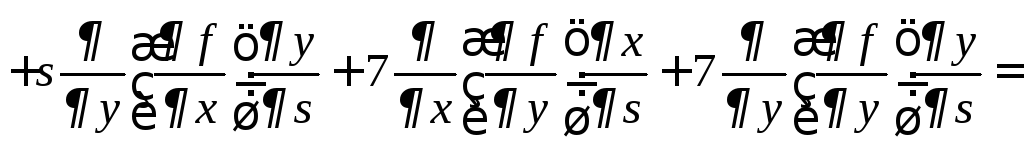
=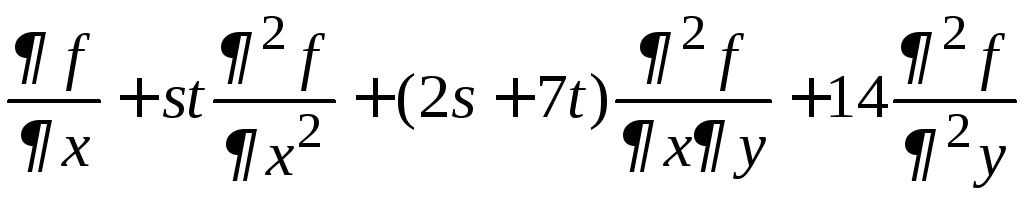 ,
,
аналогично вычисляем
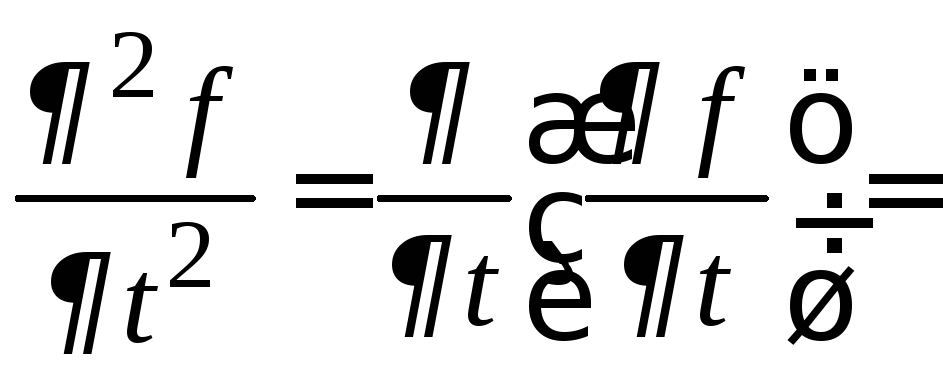
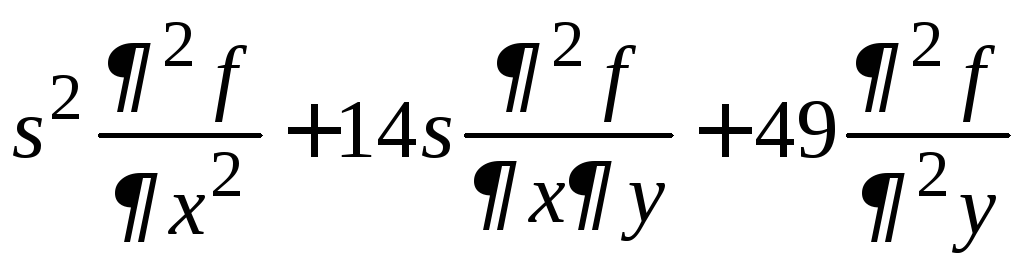 .
.
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ. ГРАДИЕНТ
Пусть l
- единичный
вектор в
![]() с координатами
с координатами![]() .
.
Производной
функции
![]() по направлению
вектора
l
в точке
по направлению
вектора
l
в точке
![]() называется
называется
![]() .
.
Производная по
направлению обозначается
![]()
![]() .
.
Градиентом
функции f
в точке
![]() называется
вектор, координатами которого являются
частные производные функции в точке:
называется
вектор, координатами которого являются
частные производные функции в точке:
grad
f
![]() = (
= (![]() ,
,![]() )
=
)
=![]() i
+
i
+![]() j.
j.
Легко показать, что производная по направлению l равна скалярному произведению вектора градиента и вектора l:
![]()
![]() =
=![]()
![]() +
+
![]() =
=![]() ,
,
где
- угол между векторами grad
f
![]() иl.
иl.
Из последней
формулы следует, что производная по
направлению вектора grad
f
![]() имеет наибольшее значение среди
производных по различным направлениям
и равна модулю вектора градиента.
имеет наибольшее значение среди
производных по различным направлениям
и равна модулю вектора градиента.
Пример 11.
Найдем производную функции
![]() в точкеМ
(1, 0)
в направлении
вектора MN
, где N
(5, 3).
в точкеМ
(1, 0)
в направлении
вектора MN
, где N
(5, 3).
Вектор MN
имеет
координаты
(4, 3),
![]() .
Значит, единичный векторl
имеет координаты (4/5, 3/5). Вычислим
частные производные в точке М:
.
Значит, единичный векторl
имеет координаты (4/5, 3/5). Вычислим
частные производные в точке М:
![]() ,
,![]() .
Тогда
.
Тогда![]() (1,0)=64/5
+ 0 3/5
= 24/5.
(1,0)=64/5
+ 0 3/5
= 24/5.
Пример 12.
Найдем производную функции
![]() в точке (2,3) в направлении вектора
градиента в этой точке.
в точке (2,3) в направлении вектора
градиента в этой точке.
Вычислим частные производные:
![]() ,
,
![]() .
.
Производная в направлении вектора градиента в точке равна модулю вектора grad f. Следовательно,
![]() .
.
КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
Для
дифференцируемой в точке
![]() функции
функции![]() верно следующее соотношение:
верно следующее соотношение:
![]() ,
,
где
![]() ,
,![]() (это следует из определения дифференциала
первого порядка). КоэффициентыА
и В
однозначно определяются:
(это следует из определения дифференциала
первого порядка). КоэффициентыА
и В
однозначно определяются:
![]()
![]() =А,
=А,
![]()
![]() =В.
=В.
Уравнение
![]()
является уравнением
плоскости, проходящей через точку
![]() .
Эта плоскость называетсякасательной
плоскостью к
графику функции
.
Эта плоскость называетсякасательной
плоскостью к
графику функции
![]() в точке
в точке![]() .
.
Таким образом,
касательной плоскостью к графику
функции
![]() в точке является такая плоскость, что
разность ее аппликаты и значения функции
в точке является такая плоскость, что
разность ее аппликаты и значения функции![]() в этой точке есть величина, бесконечно
малая по сравнению с
при
0.
в этой точке есть величина, бесконечно
малая по сравнению с
при
0.
Уравнение нормали
к графику функции
![]() в точке
в точке![]() имеет вид
имеет вид
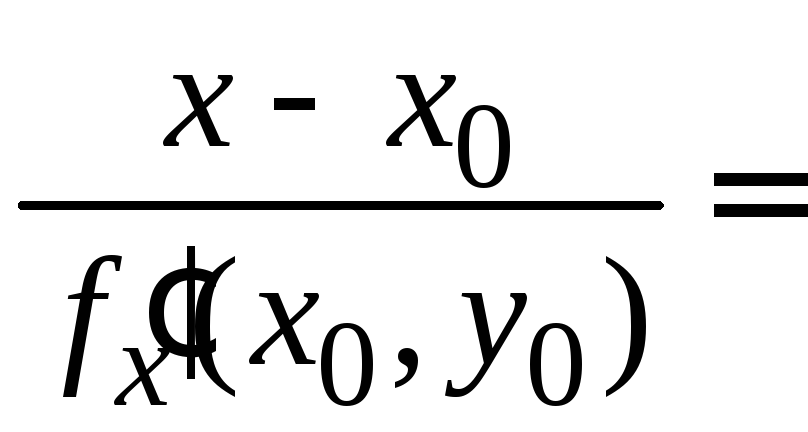
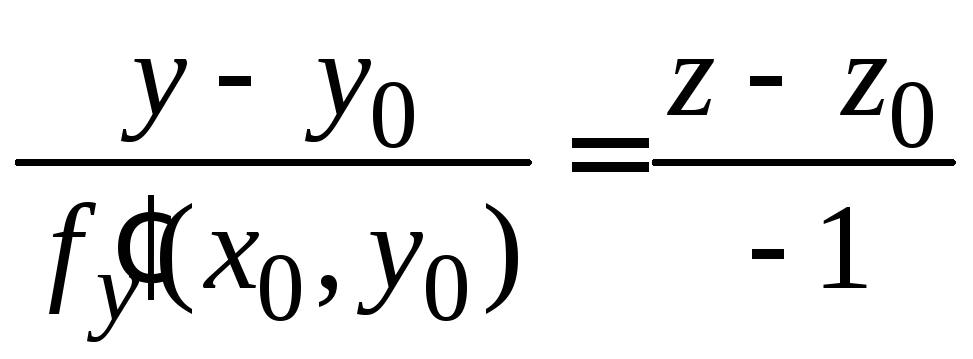 .
.
Если уравнение
гладкой поверхности задано в неявном
виде
![]() ,
то уравнение касательной плоскости в
точке
,
то уравнение касательной плоскости в
точке![]() имеет вид
имеет вид
![]()
![]() ,
,
а уравнение нормали в этой точке:
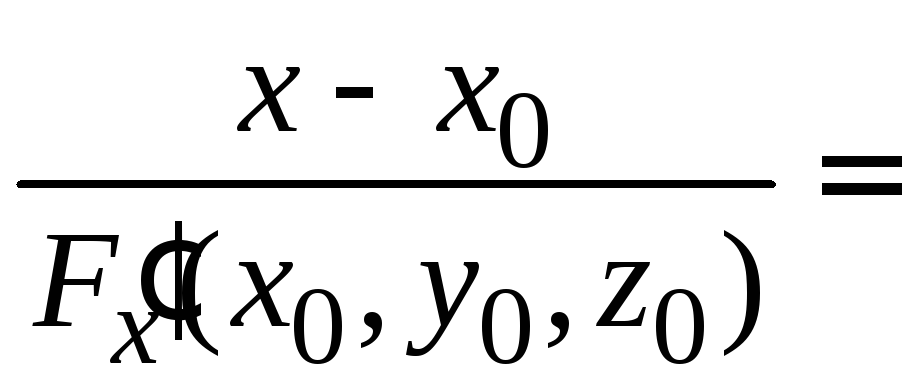
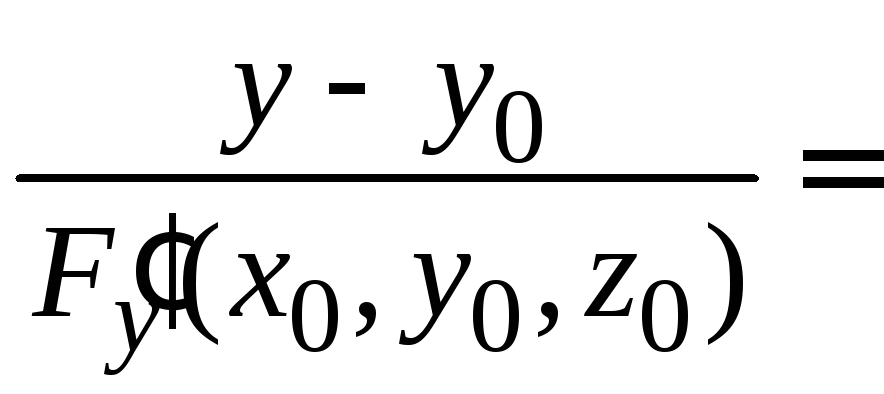
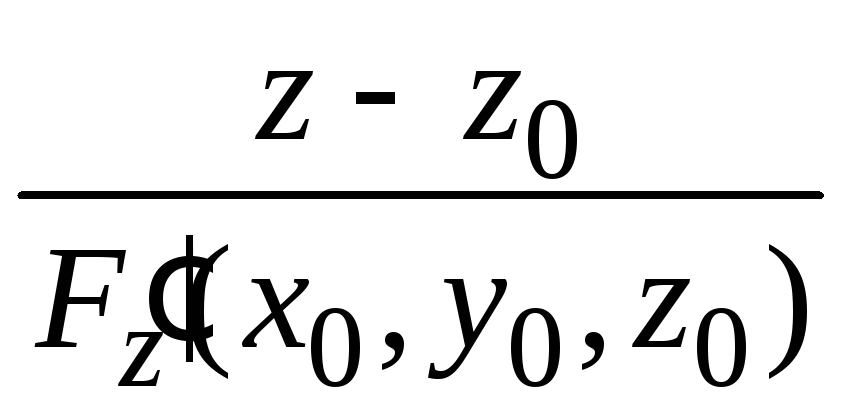 .
.
Пример 13.
Напишем уравнение касательной плоскости
и нормали к поверхности
![]() в точке (-2, 1, 4).
в точке (-2, 1, 4).
![]() ,
,
![]() .
Уравнение касательной плоскости имеет
вид:
.
Уравнение касательной плоскости имеет
вид:![]() или
или![]() .
.
Уравнение нормали:
![]() .
.
ЭКСТРЕМУМЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Точка
![]() называется точкойлокального
максимума
(локального
минимума)
функции
называется точкойлокального
максимума
(локального
минимума)
функции
![]() ,
,![]() ,
если существует окрестность точки
,
если существует окрестность точки![]() ,
для всех точек которой выполнено
неравенство
,
для всех точек которой выполнено
неравенство
![]() (
(![]() ).
).
Точки локального максимума и локального минимума функции называются точками локального экстремума.
Например, точка
(0,0) является точкой минимума функции
![]() .
.
Теорема 5
(необходимое
условие экстремума).
Если функция
![]() имеет в точке
имеет в точке![]() локальный экстремум и в этой точке
существуют частные производныеf,
то
локальный экстремум и в этой точке
существуют частные производныеf,
то
![]()
![]() =0
и
=0
и
![]()
![]() =0.
=0.
Точка
![]() называетсястационарной
точкой функции
f,
если
называетсястационарной
точкой функции
f,
если
![]()
![]() =0
и
=0
и![]()
![]() =0.
=0.
Теорема 6
(достаточное
условие экстремума).
Пусть функция
![]() дважды непрерывно дифференцируема в
некоторой окрестности стационарной
точки
дважды непрерывно дифференцируема в
некоторой окрестности стационарной
точки![]() .
.
Обозначим =![]()
![]()
![]()
![]() -
(
-
(![]()
![]() )2.
Тогда
)2.
Тогда
1) если >0,
то в точке
![]() функцияf
имеет
локальный экстремум: максимум при
функцияf
имеет
локальный экстремум: максимум при
![]()
![]() >
0 и минимум при
>
0 и минимум при![]()
![]() <
0;
<
0;
2) если <0,
то в точке
![]() функцияf
не имеет экстремума;
функцияf
не имеет экстремума;
3) если =0,
то в точке
![]() функцияf
может иметь
локальный экстремум, а может и не иметь
его (в этом случае требуются дополнительные
исследования).
функцияf
может иметь
локальный экстремум, а может и не иметь
его (в этом случае требуются дополнительные
исследования).
Пример 14. Исследуем на экстремум функцию
![]() .
.
Отметим, что функция
u
определена
и дифференцируема на всей плоскости.
![]() ,
,![]() .
Приравнивая частные производные к нулю
и решая полученную систему, находим
стационарные точки функции: (2, 1), (1, 2),
(-2, -1), (-1, -2).
.
Приравнивая частные производные к нулю
и решая полученную систему, находим
стационарные точки функции: (2, 1), (1, 2),
(-2, -1), (-1, -2).
=![]() =
=![]() .
.
(2, 1) = 36∙(1 - 4) = -108 < 0, поэтому в точке (2, 1) экстремума нет.
(1, 2) = 36∙(4 - 1) = 108
> 0,
![]() ,
следовательно, в точке (1, 2) функция имеет
минимум,
u(1,2)
= -25.
,
следовательно, в точке (1, 2) функция имеет
минимум,
u(1,2)
= -25.
(-2, -1) = 36∙(1 – 4 ) = -108 < 0, в точке (-2, -1) экстремума нет.
(-1, -2) = 36∙(4 - 1) =
108 > 0,
![]() ,
следовательно, в точке (-1, -2) функция
имеет максимум,
u(-1,
-2) = 31.
,
следовательно, в точке (-1, -2) функция
имеет максимум,
u(-1,
-2) = 31.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ
Пусть функция
![]() непрерывна на ограниченном замкнутом
множествеD.
непрерывна на ограниченном замкнутом
множествеD.
Напомним, что
множество
![]() называетсяограниченным,
если существует такая окрестность U
(0,0), что
называетсяограниченным,
если существует такая окрестность U
(0,0), что
![]() U
(0,0); множество
U
(0,0); множество
![]() называетсязамкнутым,
если оно содержит все свои предельные
точки.
называетсязамкнутым,
если оно содержит все свои предельные
точки.
По теореме
Вейерштрасса существуют такие точки
![]() и
и![]() ,
что
,
что![]() является наибольшим значением функции
на множествеD
, а
является наибольшим значением функции
на множествеD
, а
![]() - наименьшим ее значением на множествеD.
- наименьшим ее значением на множествеD.
Функция, дифференцируемая в ограниченной области и непрерывная на ее границе, достигает своего наибольшего и наименьшего значений либо в стационарных точках, либо в граничных точках D.
Пример
15. Найдем
наибольшее и наименьшее значения функции
![]() на множествеD,
ограниченном прямыми
на множествеD,
ограниченном прямыми
![]() ,
,![]() ,
,![]() .
.

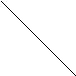 y
(2, 1), (1, 2),
(-2, -1), (-1, -2) - стационарные
y
(2, 1), (1, 2),
(-2, -1), (-1, -2) - стационарные
точки функции u (см. пример 14), но (-2,-1),
(-1,-2) не принадлежат D.
u (2, 1) = -23, u (1, 2) = -25.
D Изучим поведение функции u на
x границе множества D.
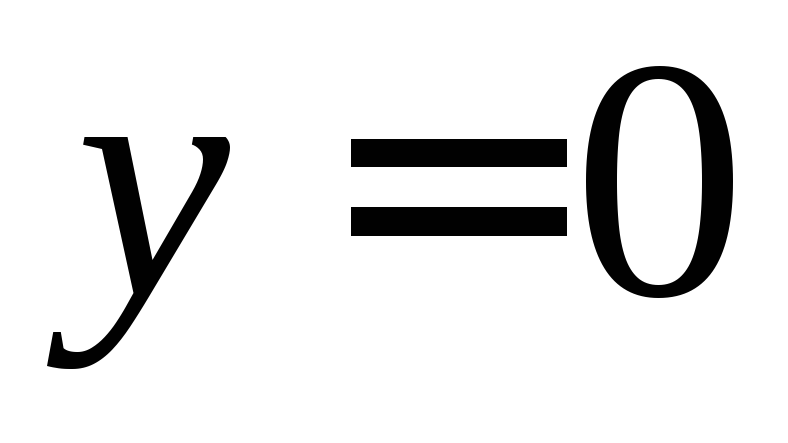 ,
,
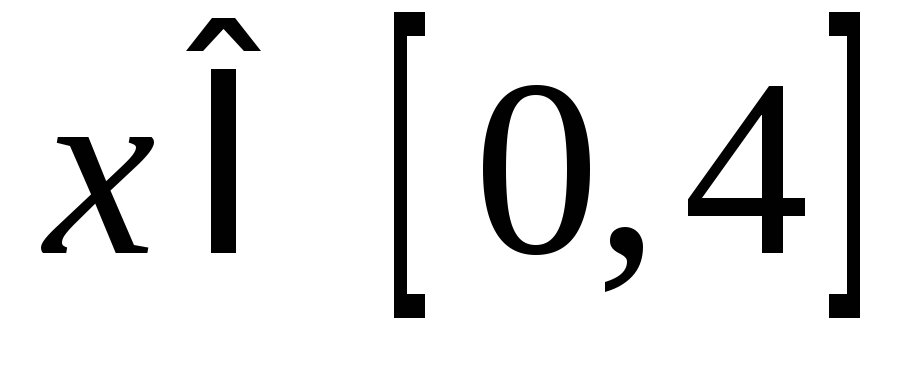 .
На этом участке границы
.
На этом участке границы
Рис. 5
![]() .
Это функция одной переменной,
.
Это функция одной переменной,
которая
принимает наименьшее значение в точке
![]() ,
а наибольшее значение в точке
,
а наибольшее значение в точке![]() :u
(4,0) = -45, u
(0,0)= 3;
:u
(4,0) = -45, u
(0,0)= 3;
2)
![]() ,
,![]() .
На этом отрезке
.
На этом отрезке![]() .
Для того чтобы найти наименьшее и
наибольшее значения функции на отрезке,
вычислим ее значения в стационарных
точках и на концах отрезка:
.
Для того чтобы найти наименьшее и
наибольшее значения функции на отрезке,
вычислим ее значения в стационарных
точках и на концах отрезка:![]() ;
;![]() ,
но
,
но![]() ,
поэтому вычисляемu
(0,0) = 3, u
(0,
,
поэтому вычисляемu
(0,0) = 3, u
(0,![]() )=
=
)=
=
![]() ,
u
(0,4) = 7.
Наибольшим является значение в точке
(0,4), а наименьшим - в точке (0,
,
u
(0,4) = 7.
Наибольшим является значение в точке
(0,4), а наименьшим - в точке (0,
![]() );
);
3)![]()
![]() ,
,![]() .
Здесь
.
Здесь
![]()
![]()
![]() .
.
Вычисляем значения
функции в стационарных точках и на
концах отрезка:
![]() ;
;![]() ;u
(0,4)= 7, u
(3/2, 5/2) = -20,
u
(5/2,3/2)= -18, u
(4,0)= -45. На
этом участке границы наибольшим
является значение функции в точке (0,4),
а наименьшим - в точке (4,0).
;u
(0,4)= 7, u
(3/2, 5/2) = -20,
u
(5/2,3/2)= -18, u
(4,0)= -45. На
этом участке границы наибольшим
является значение функции в точке (0,4),
а наименьшим - в точке (4,0).
Из полученных в пунктах 1)-3) наименьших и наибольших значений функции на различных участках границы и из значений функции в стационарных точках выбираем самое большое и самое маленькое. Наибольшее значение: u (0,4)= 7, наименьшее значение: u (4,0)= -45.
