Дифференцирование функций комплексной переменной

Определение производной:

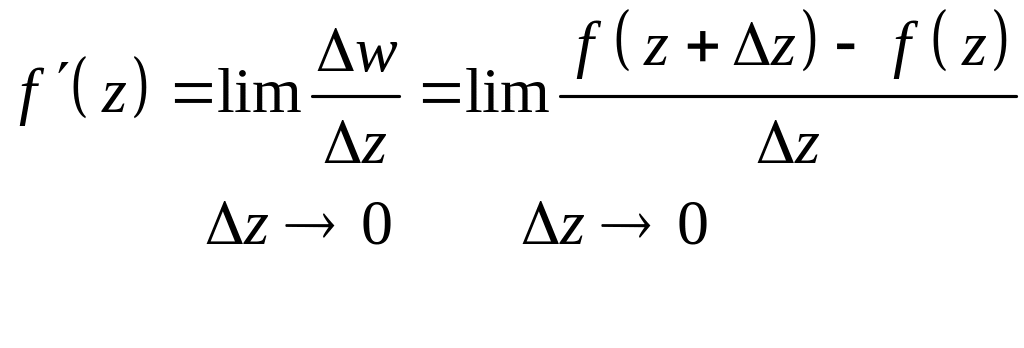. (1)

Пусть при фиксированном , т.е. . Т.к.

, (2)

то по опр. (1) мы должны продифференцировать (2) по . Поэтому

находим

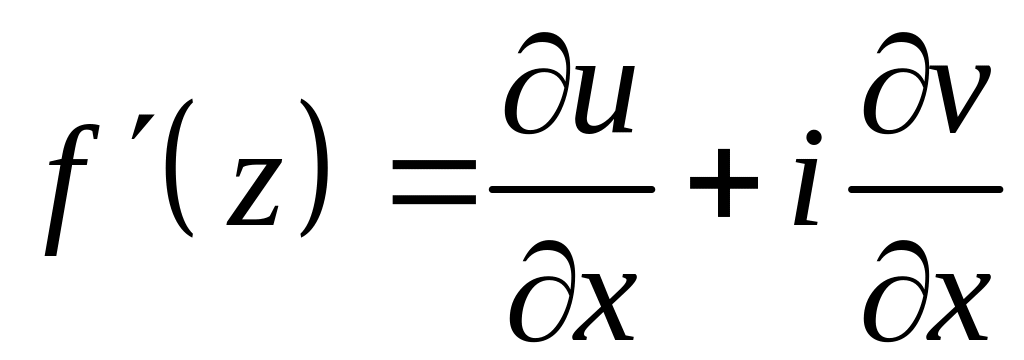. (3)

Пусть при фиксированном , т.е. . Поэтому находим

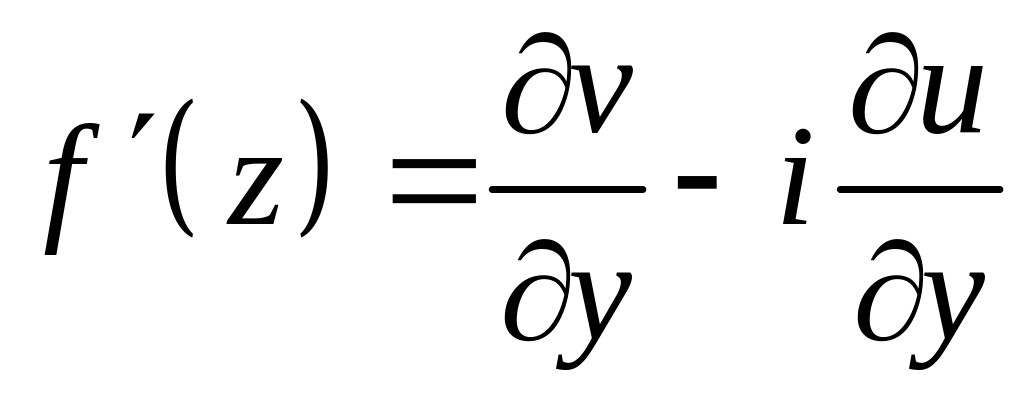. (4)

Следовательно, должны выполняться условия

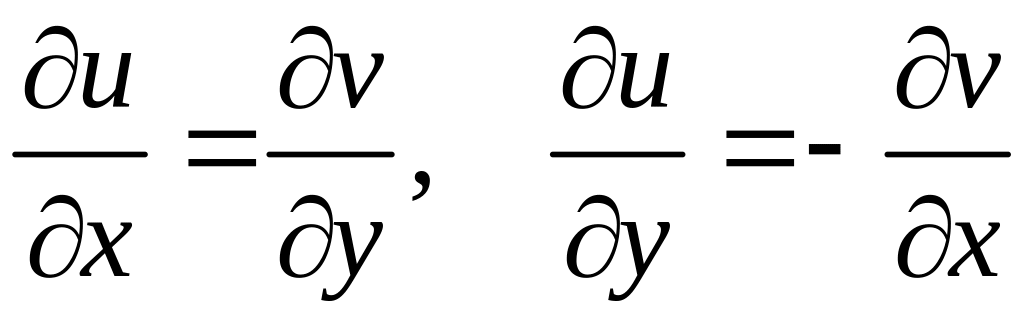. (5)

Ф. (5) – ус-я Даламбера – Эйлера или Коши - Римана.

Имеет место теорема:

Если ф. определена в некоторой окрестности точки , причем в этой точке функции дифференцируемы, то для дифференцируемости ф. в точке необходимо и достаточно, что бы в этой точке выполнялись равенства

.

Справедливы обычные правила дифференцирования:

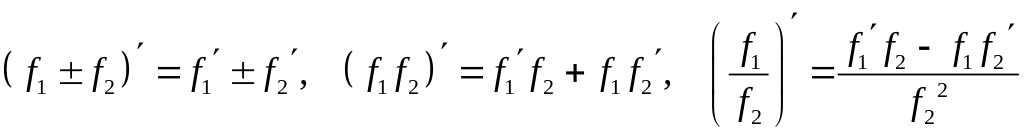. (6)

Правило дифференцирования сложной функции

Если дифференцируема в т. , а дифференцируема в точке , то

. (7)

Если в некоторой т. ф. дифференцируема и существует ф.

, дифференцируемая в т. , тогда

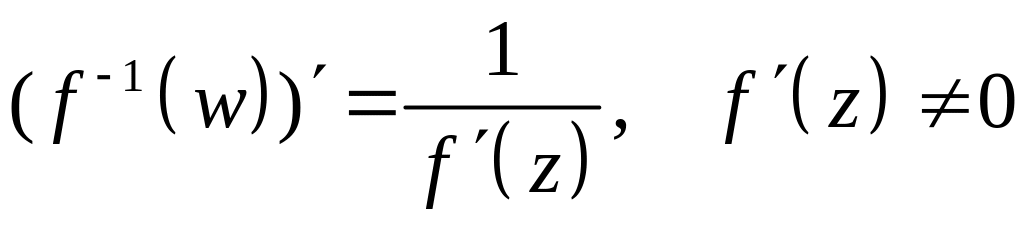. (8)

Т. о дифференцируемости основных элементарных ф. комплексной переменной:

Ф. дифференцируемы в любой т. комплексной плоскости; ф. дифференцируемы в любой т. комплексной плоскости, кроме т.

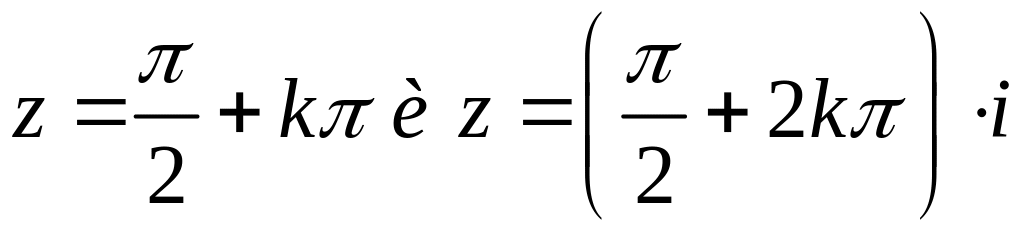
соответственно; для ф. Lnz и в окрестности каждой т. можно выделить однозначную ветвь, которая дифференцируема в

т. .

Выполняются обычные правила

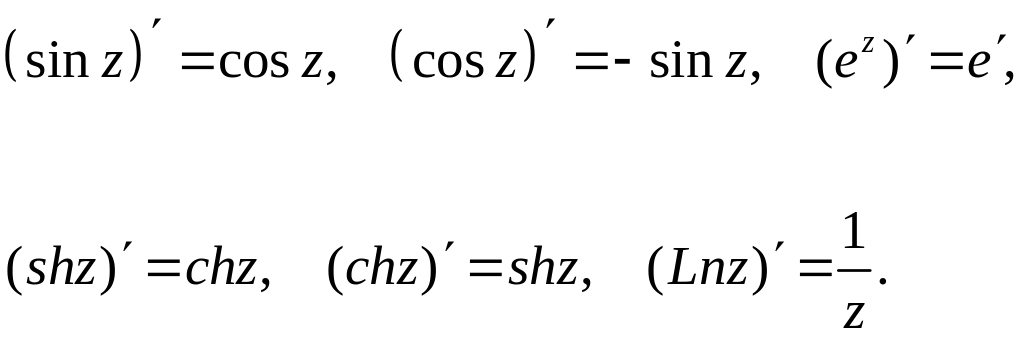и т.д. (9)

Для всех ветвей Lnz получилась одна и та же производная, т.к. различные ветви Lnz отличаются на постоянную .

Аналитическая функция. Дифференциал.

Опр. Однозначная ф. называется аналитической или голоморфной в т. z, если она дифференцируема в некоторой окрестности этой точки, включая и саму точку z.

Опр. Ф. наз. аналитической в области D, если она дифференцируема в каждой точке этой области.

Опр. Точки, в которых однозначная ф. аналитична, наз. правильными точками . Точки, в которых не является аналитической, наз. особыми точками этой функции.

Пусть ф. аналитична в т.z. Тогда

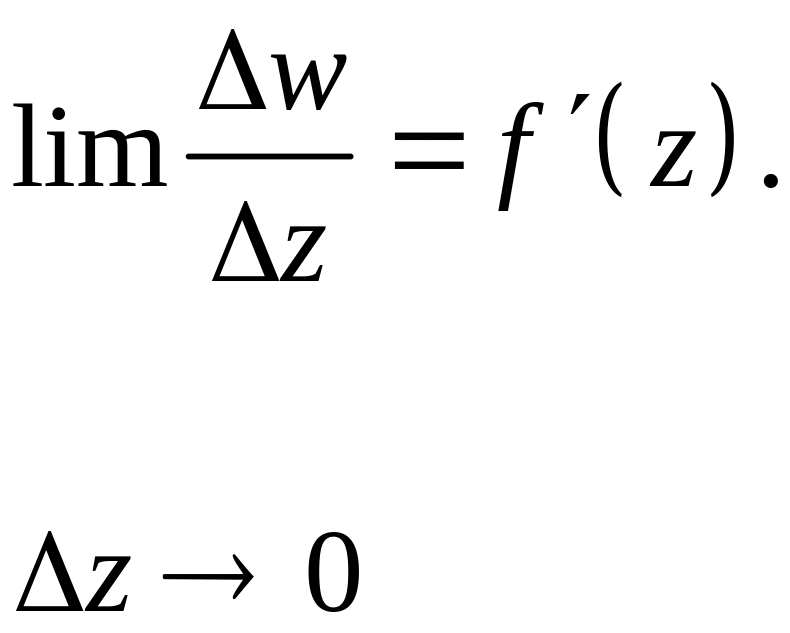(1)

Поэтому

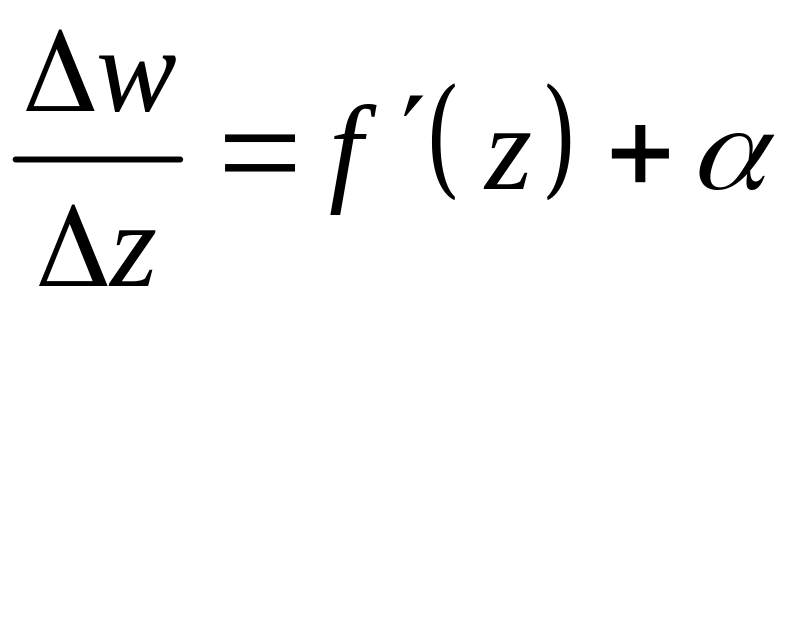, где . (2)

Тогда

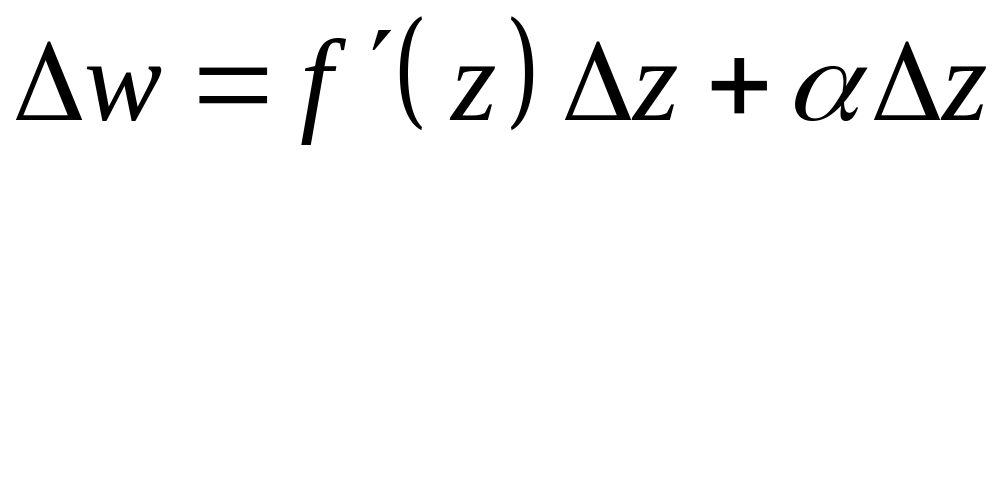. (3)

Пусть , тогда первое слагаемое в (3) является при

является бесконечно малой того же порядка, что и Второе слагаемое – бесконечно малая более высокого порядка, чем Следовательно, первое слагаемое составляет главную часть приращения функции

.

Опр. Дифференциалом аналитической ф. в точке z наз. главная часть ее приращения в этой точке, т.е.

(4)

Но в частном случае имеем

. (5)

Поэтому соотношение (4) принимает вид

(6)

Отсюда следует, что

.

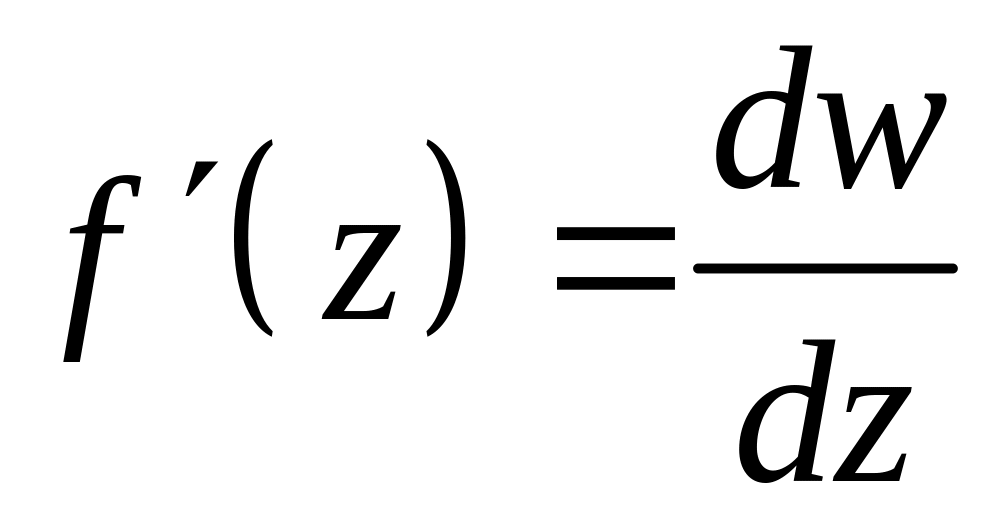Замечание. Если ф. аналитична в некоторой области D, то

выполняются ф.

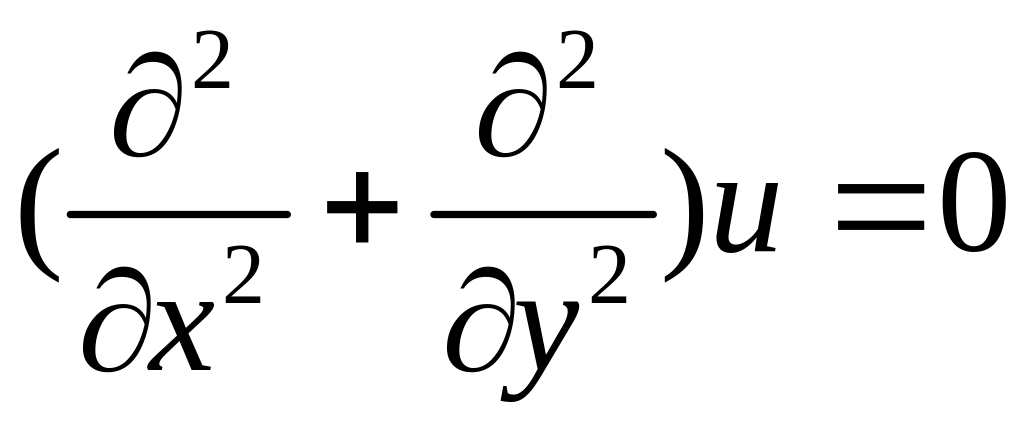, (7)

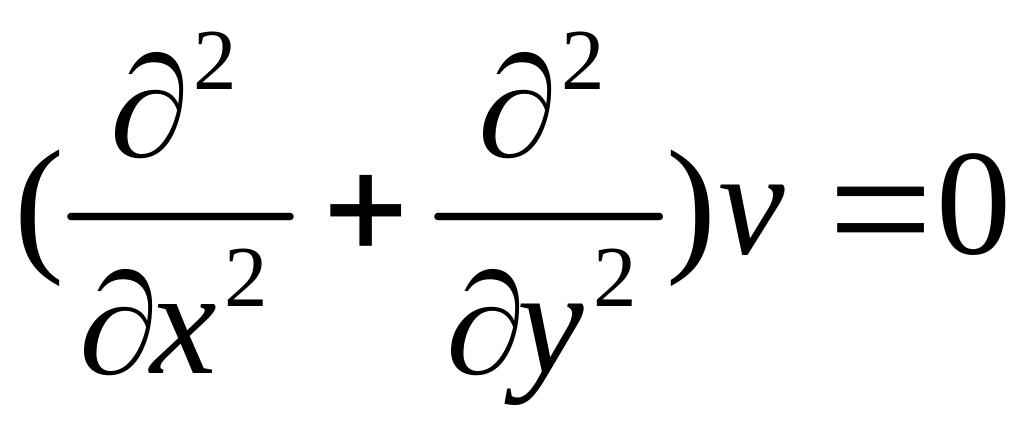. (8)

Уравнения (7), (8) наз. уравнениями Лапласа.

ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА КОНФОРМНОГО ОТОБРАЖЕНИЯ

Непрерывное отображение w = f (z) области D комплексной плоскости С в плоскость С называется конформным в точке D, если в этой точке оно обладает свойствами постоянства искажения масштаба и сохранения углов. Свойство постоянства искажения масштаба (или постоянства растяжений) в точке при отображении w = f (z) состоит в том, что при отношение 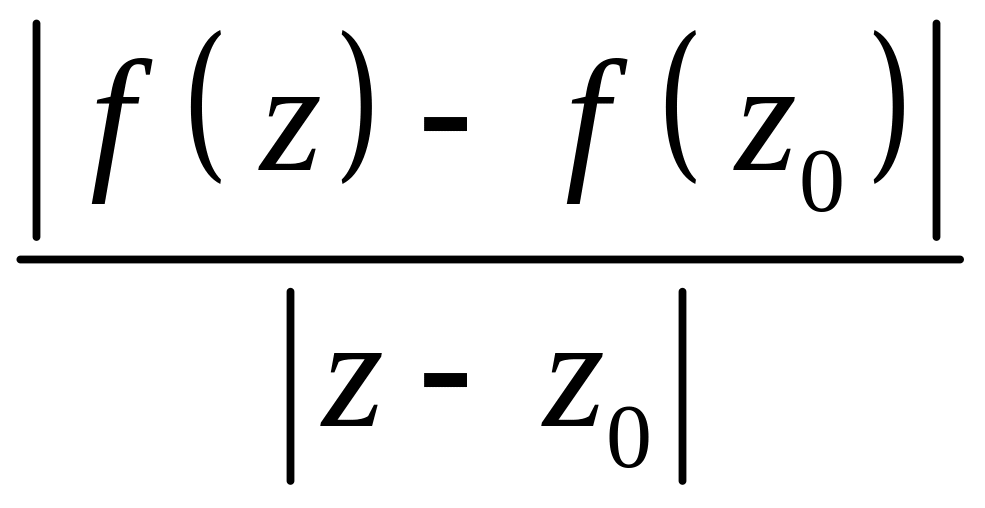расстояния между образами f (z) и точек z и к расстоянию между самими точками z и стремится к определенному пределу k, не зависящему от способа стремления z к . Число k называется коэффициентом искажения масштаба (или коэффициентом растяжения) в точке при отображении w = f (z). Свойство сохранения (консерватизма) углов в точке при отображении w = f (z) состоит в том, что любая пара гладких ориентированных кривых g1 , g2 , расположенных в D и пересекающихся в точке под некоторым углом (то есть имеющих касательные в точке , образующие между собой угол ), переходит при рассматриваемом отображении в пару гладких кривых G1 , G2 , пересекающихся в точке под тем же углом с учетом направления . Такое отображение называют еще конформным отображением первого рода. Если отображение сохраняет углы между кривыми по абсолютной величине, изменяя их направления на противоположные, то оно называется антиконформным или конформным отображением второго рода. Отображение области D называется конформным, если оно конформно в каждой точке области.

Из определения конформного отображения непосредственно следует, что если в плоскости изменения комплексной переменной z взять достаточно малый треугольник с одной из вершин в точке , то он при конформном отображении w = f (z) перейдет в малый криволинейный треугольник с вершиной в точке . При этом соответственные углы у этих треугольников будут равны как по абсолютной величине, так и по направлению, а отношения их соответственных сторон будут мало отличаться от коэффициента k искажения масштаба. Таким образом, конформное отображение является отображением, сохраняющим форму достаточно малых фигур, то есть преобразованием подобия применительно к малым фигурам.

Теор. Если ф. аналитична в области D, причем во всех точках области , то отображение конформно в области D.