
- •Комплексные числа
- •Дифференцирование функций комплексной переменной
- •Интеграл от функции комплексной переменной
- •Интегральная теорема Коши.
- •Первообразная аналитической функции.
- •Теория интегралов Коши.
- •Применение интегральных формул Коши к вычислению интегралов.
- •Ряды Тейлора.
- •Бесконечно удаленная точка
- •Ряды Лорана.
- •Изолированные особые точки.
- •Вычет аналитической функции в особой точке.
- •Вычет в существенно особой точке находится из разложения функции в ряд Лорана.
- •Бесконечно удалённая особая точка.
Лекция №1
Комплексные числа
Комплексным
числом z
наз. упорядоченная пара действительных
чисел
![]() ,
над которыми определены алгебраические
операции (сложение, вычитание, умножение)
по определенным правилам.
,
над которыми определены алгебраические
операции (сложение, вычитание, умножение)
по определенным правилам.
Опр.
![]() -
действительная часть,
-
действительная часть,
![]() -
мнимая часть.
-
мнимая часть.
Комплексные
числа
![]() и
и
![]() наз. равными, если
наз. равными, если
![]() ,
,
![]() .
.
Опр.
Суммой комплексных чисел
![]() и
и
![]() наз. комплексное число
наз. комплексное число
![]() .
Пишут
.
Пишут
![]() .
.
Св-ва
![]() =
=![]() - коммутативность
- коммутативность
![]() -
ассоциативность.
-
ассоциативность.
Опр. нуля
![]() .
.
Св-во:
![]() .
.
Опр. произведения комплексных чисел:
![]() .
.
Будем рассматривать действительные числа как комплексные
![]() .
.
При этом сохраняются все известные правила действий над действительными числами.
Опр.
Комплексное число
![]() наз. чисто мнимым и обозначается
символически
наз. чисто мнимым и обозначается
символически
![]() .
Комплексное число
.
Комплексное число
![]() наз. мнимой единицей.
наз. мнимой единицей.
Сво-во:
=![]() ,
,
![]() .
.
Поэтому комплексные числа можно записывать в алгебраической форме
![]() .
.
Теперь операции сложения и умножения можно производить по обычным правилам алгебры многочленов.
Опр.
Разностью
![]() наз.
наз.
![]() .
.
Опр.
Число
![]() наз. комплексно сопряженным числу
наз. комплексно сопряженным числу
![]() .
.
Опр. Частным комплексных чисел и наз. такое число , что
![]() .
.
Отсюда находим
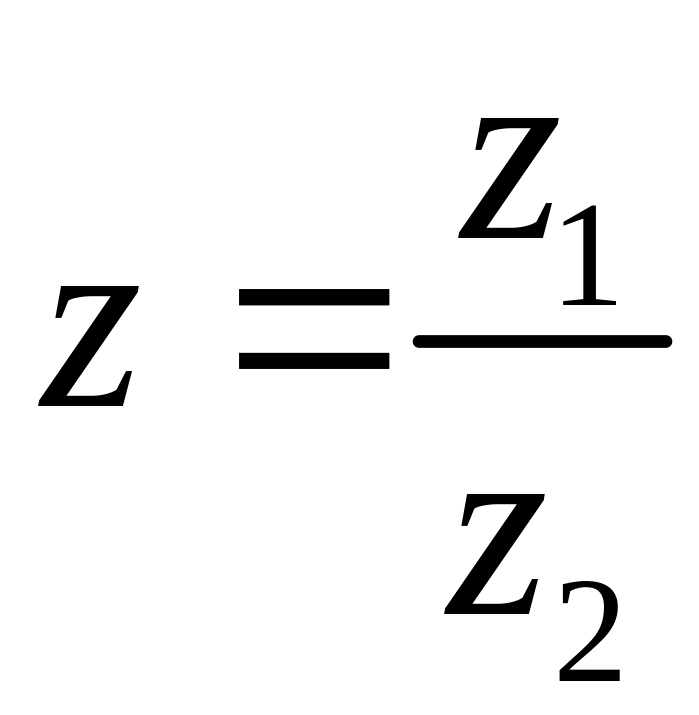 =
=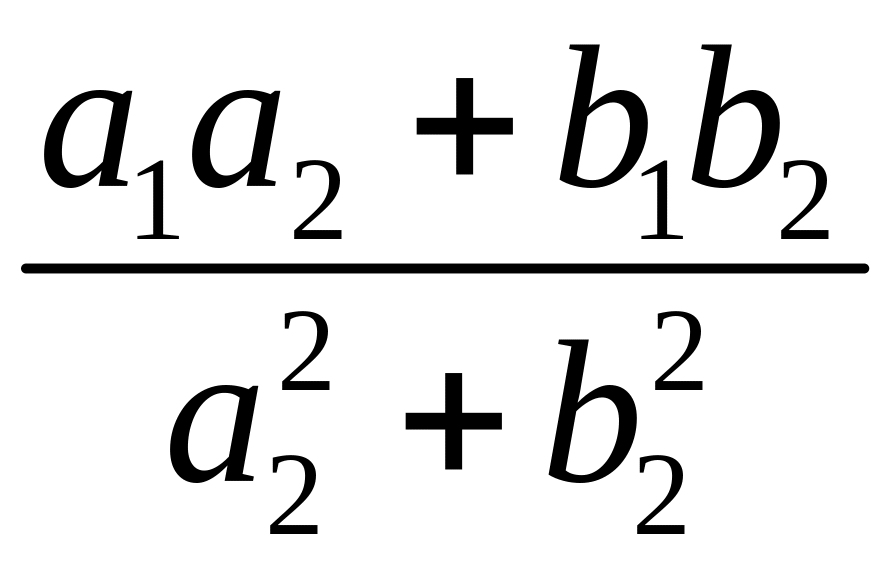 +
+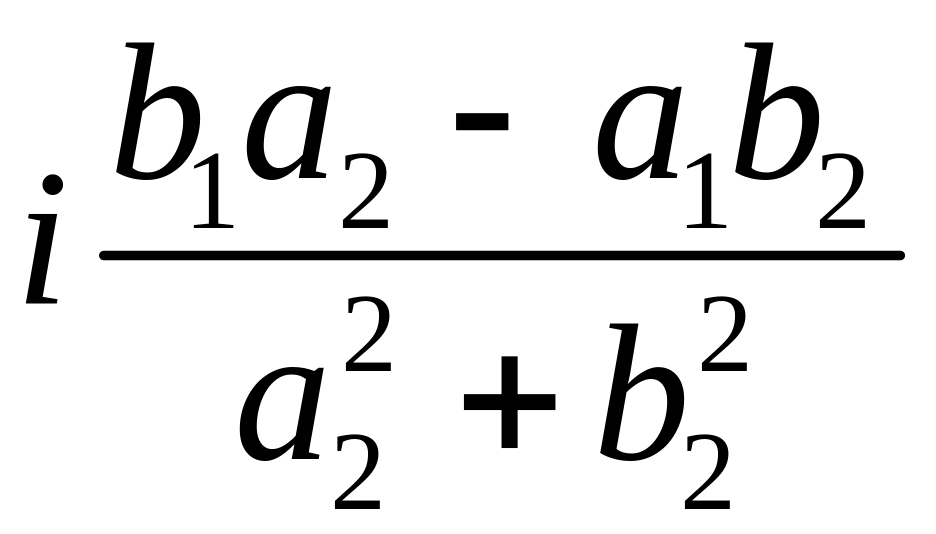 .
.
Тот же результат получим, используя алгебраическую форму записи комплексных чисел:
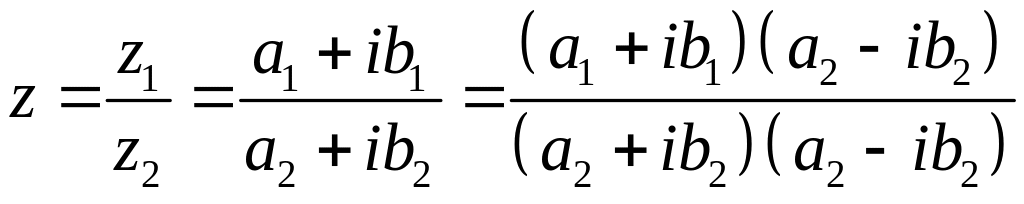 .
.
Комплексная плоскость
О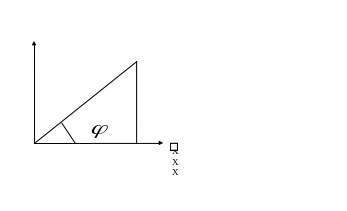
Положительное
направление угла
![]() - направление против часовой стрелки.
Очевидно
- направление против часовой стрелки.
Очевидно
![]() .
.
Опр.
![]() -
модуль комплексного числа,
-
аргумент комплексного числа.
-
модуль комплексного числа,
-
аргумент комплексного числа.
Обозначение
![]() .
.
Очевидно
 .
.
При
выборе значения
следует учитывать знаки
![]() и
и
![]() .
.
![]() не определен.
не определен.
![]()
Величина
![]() наз. главным значением аргумента.
наз. главным значением аргумента.
Принимают
![]() или
или
![]() .
.
Опр.
Показательной функцией
![]() называется
величина
называется
величина
![]() .
.
При
таком определении
![]() -
обычное св-во экспоненты. Положив здесь
-
обычное св-во экспоненты. Положив здесь
![]() ,
получим
,
получим
![]() - формула
Эйлера.
- формула
Эйлера.
Геометрически комплексные числа складываются как векторы.
Неравенство треугольника
![]() .
.
Из формулы Эйлера непосредственно имеем
![]() -
комплексное число в показательной
форме.
-
комплексное число в показательной
форме.
Далее имеем
![]() .
.
Т.о., при умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Далее имеем
![]() - формула
Муавра.
- формула
Муавра.
Деление
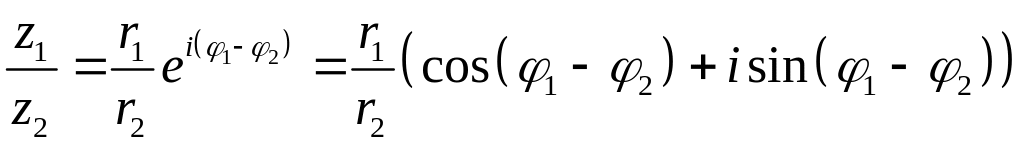 .
.
Корнем
![]() -ой
степени из
наз. комплексное число
-ой
степени из
наз. комплексное число
![]() ,
удовл. равенству
,
удовл. равенству
![]() ,
т.е. w=
,
т.е. w=![]() .
.
Положим
![]() .
.
Тогда по формуле Муавра
![]() .
.
Отсюда
![]() .
.
Далее
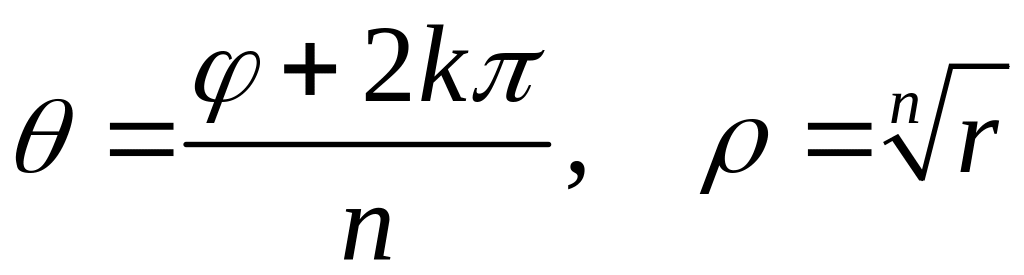 (арифм.
корень) .
(арифм.
корень) .
Поэтому
w=
=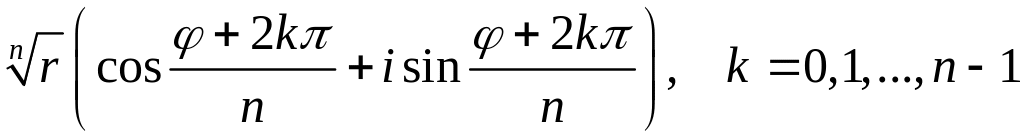 .
.
Получим различных значений корня.
Функции комплексного переменного
![]() .
(1)
.
(1)
![]() .
(2)
.
(2)
![]() .
(3)
.
(3)
![]() .
(4)
.
(4)
Пределом
последовательности {![]() }
наз. число
}
наз. число
![]() :
:
![]() .
.
Число
![]() наз. пределом ф.
наз. пределом ф.
![]() в
точке
,
если
в
точке
,
если
![]() .
.
Ф. наз. непрерывной в т. , если
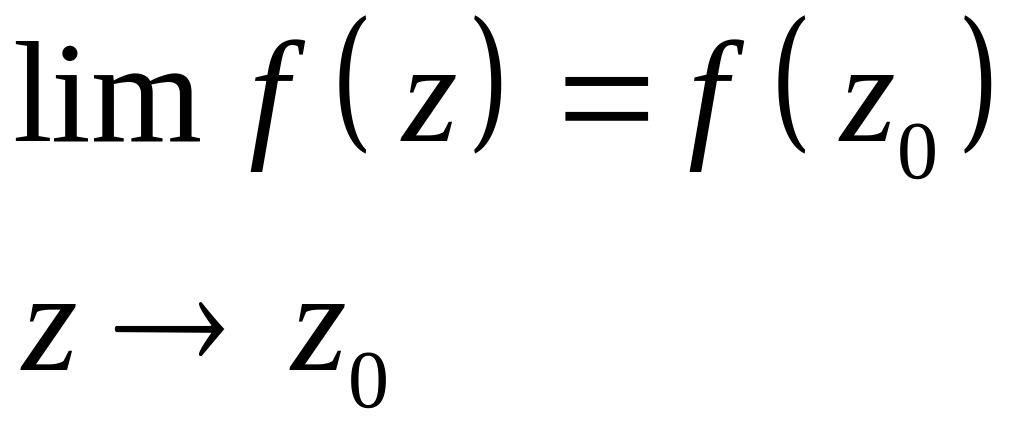 (5)
(5)
Показательная ф. определяется по формуле
. (6)
Из опр. вытекает
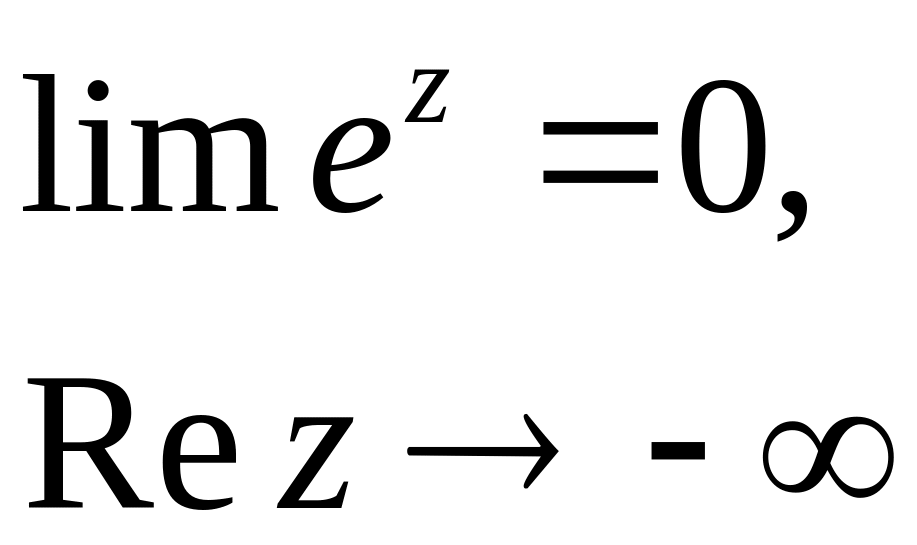
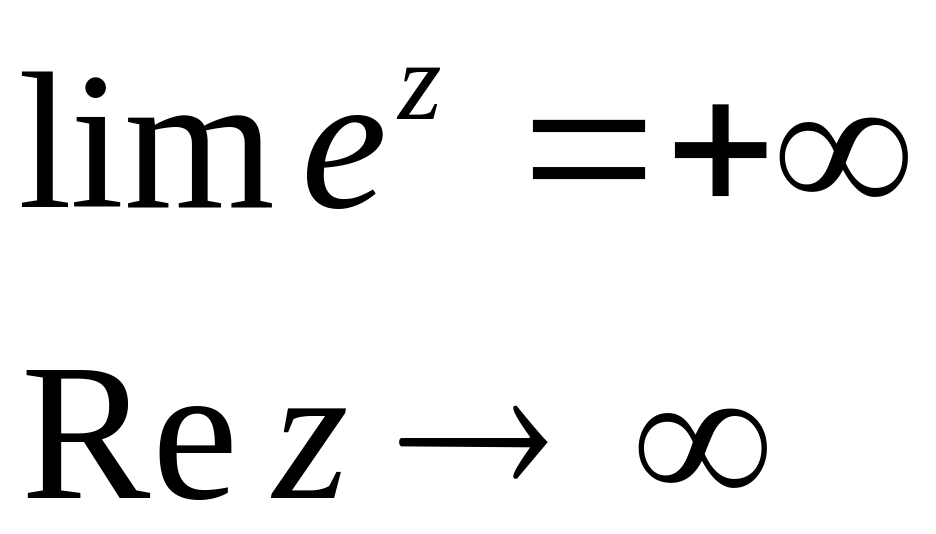
Выражение
при
![]() не имеет смысла.
не имеет смысла.
Логарифмическая ф. определяется формулой
![]() .
(7)
.
(7)
Имеем
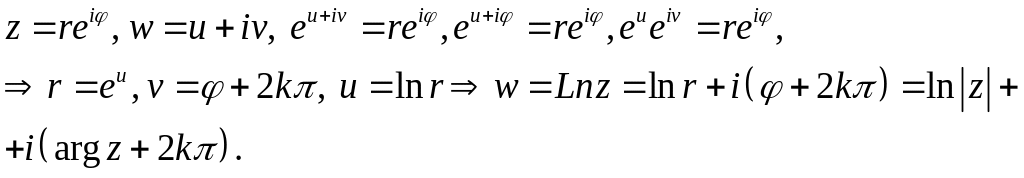 (8)
(8)
Опр. Главным значением логарифма наз.
![]() ,
. (9)
,
. (9)
Т.о., каждое комплексное число z имеет бесконечное множество логарифмов (8).
Тригонометрические функции
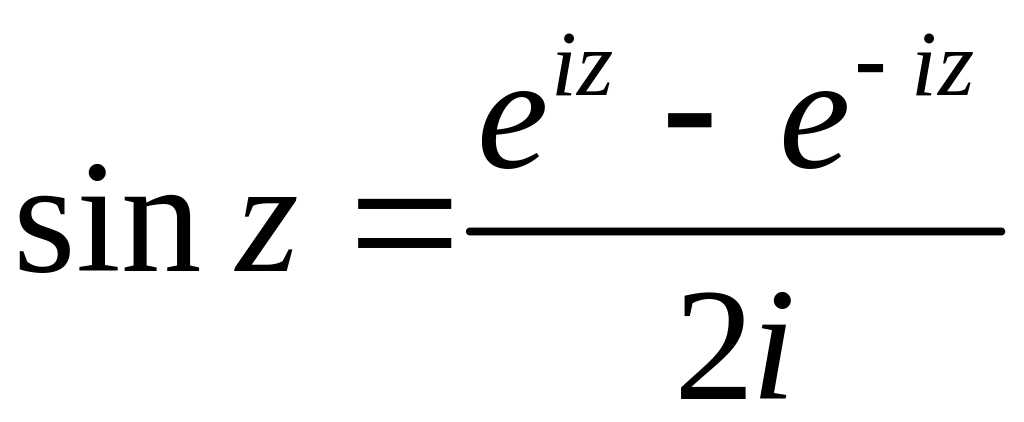 ,
(10)
,
(10)
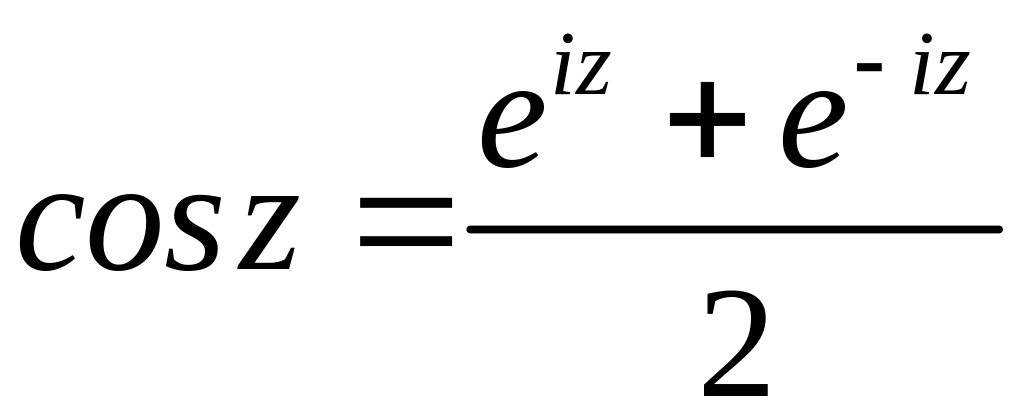 ,
(11)
,
(11)
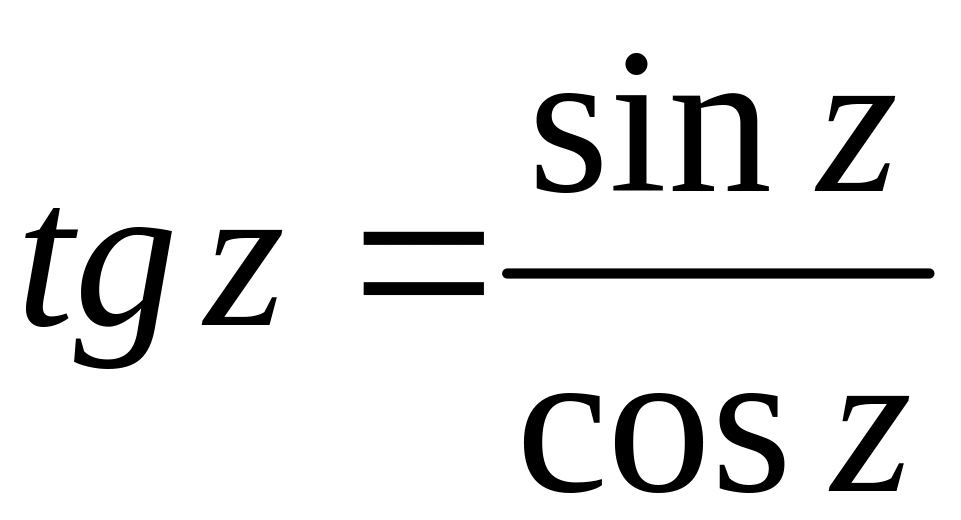 ,
(12)
,
(12)
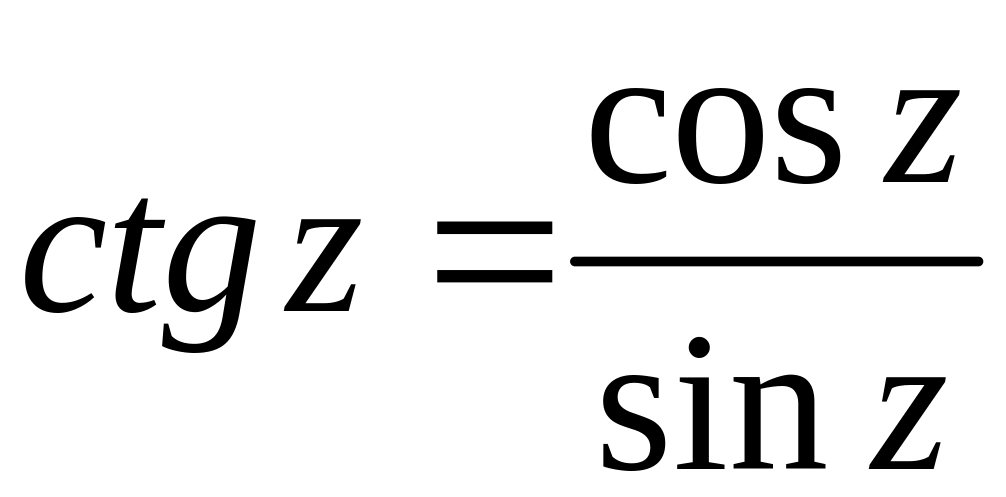 .
(13)
.
(13)
Сохраняются все обычные тригонометрические формулы
![]() (14)
(14)
![]() ,
(15)
,
(15)
![]() (16)
(16)
и т.д.
Однако
![]() и
и
![]() неограничены в комплексной плоскости.
неограничены в комплексной плоскости.
Найдем ф., обратную синусу. Имеем
![]()
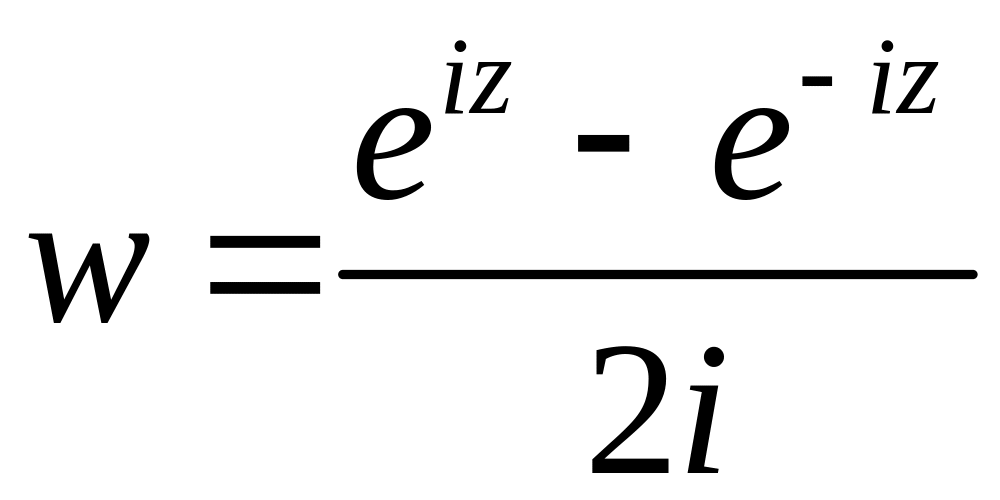 ,
,
![]() ,
,
![]() или
или
![]() .
.
Решая
квадратное ур-е отн.
![]() ,
получим
,
получим
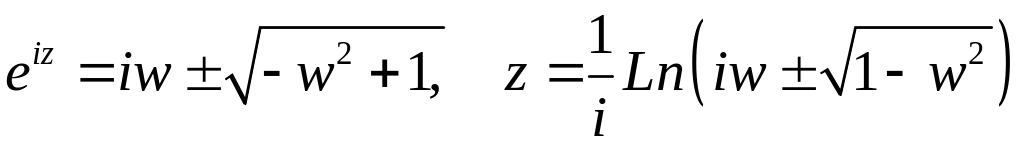 .
(17)
.
(17)
Обозначим найденное значение
![]() .
Тогда имеем многозначную функцию
.
Тогда имеем многозначную функцию
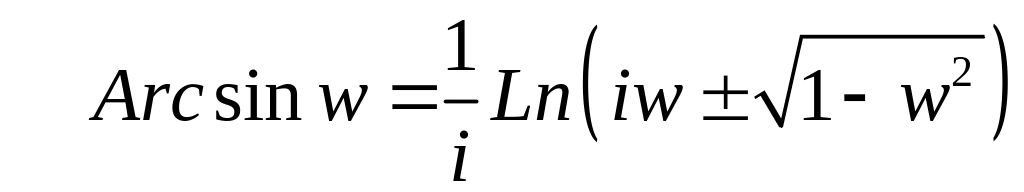 .
(18)
.
(18)
Ее главное значение
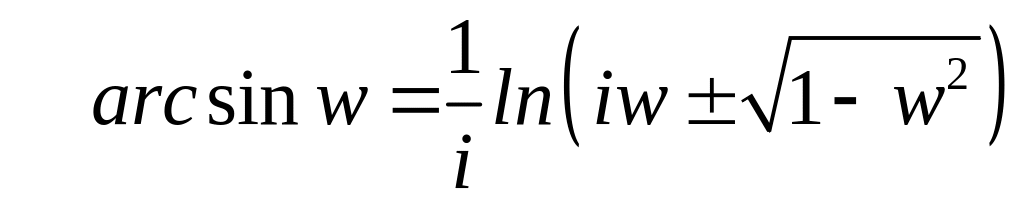 .
(19)
.
(19)
Функция
![]() имеет две однозначные ветви. Знак
имеет две однозначные ветви. Знак
![]() можно не указывать, т.к. квадратный
корень – двузначная функция.
можно не указывать, т.к. квадратный
корень – двузначная функция.
Общая степенная ф. определяется соотношением
![]()
![]() ,
(20)
,
(20)
где
![]() -
может быть комплексным числом. При
-
может быть комплексным числом. При
![]() ф.
ф.
![]() всегда имеет бесконечно много значений.
всегда имеет бесконечно много значений.
Общая показательная ф.
![]() .
(21)
.
(21)
Ф. (21) – совокупность отдельных однозначных ф., отличающихся множителями
![]() .
.
Гиперболические ф. определены формулами
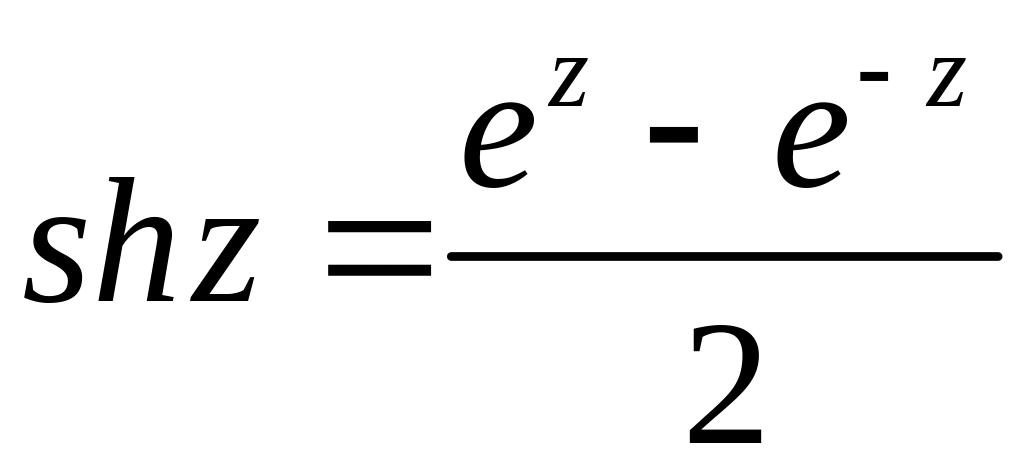 ,
,
 ,
,
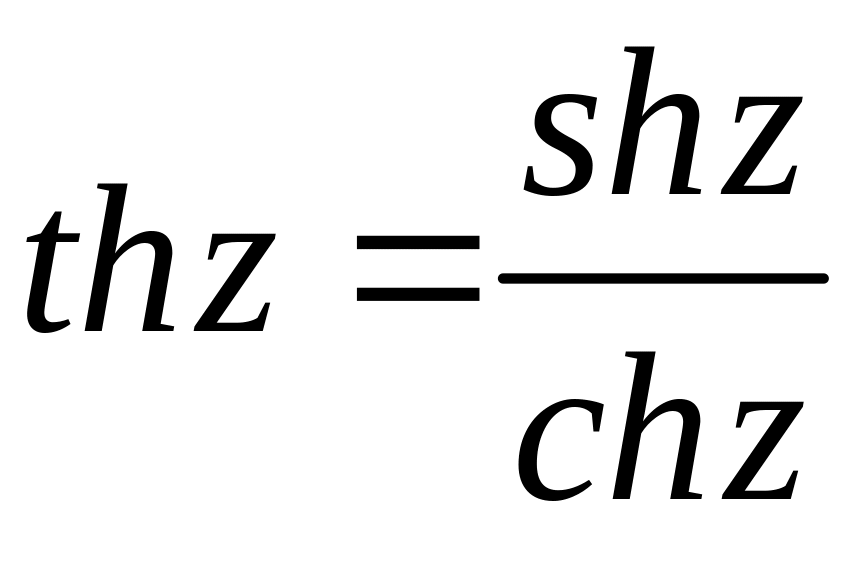 ,
,
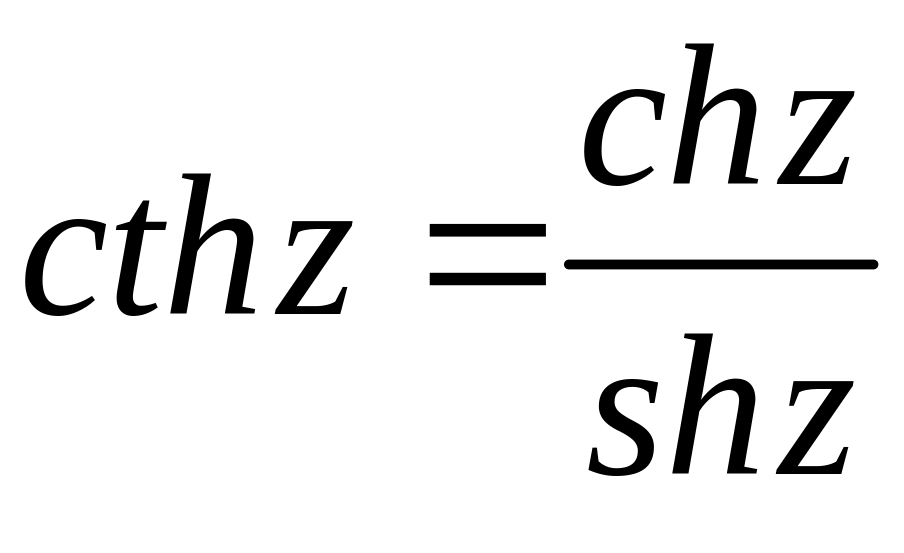 .
(22)
.
(22)
