1.6. Линейные неоднородные дифференциальные уравнения

Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде: . При этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением (P(x) и Q(x) – функции, непрерывные на некотором промежутке a < x < b).

Метод Бернулли. Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций , где u=u(x) и v=v(x) – неизвестные функции от х. Отсюда, .

Подставляя у и в исходное уравнение, получаем:

.

В качестве u берут частное решение уравнения: . Решая это дифференциальное уравнение, определяем u:

.

Для нахождения второй неизвестной функции v подставим полученное выражение для функции u в исходное уравнение с учетом того, что выражение, стоящее в скобках, равно нулю.

.

Интегрируя, получаем функцию v: .

Подставляя полученные значения u и v в y=uv, получаем:

.

Окончательно получаем формулу: .

Это уравнение является решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.

Метод Лагранжа. Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной.

Первый шаг: приравниваем правую часть дифференциального уравнения к нулю: .

Находится решение получившегося однородного дифференциального уравнения: .

Второй шаг: находим решение неоднородного дифференциального уравнения. Для этого считаем постоянную С₁ некоторой функцией от х. Тогда по правилам дифференцирования произведения функций получаем:

.

Подставляем полученное равенство в исходное уравнение:

.

Упрощаем, преобразуем и получаем: .

Отсюда: .

Подставляя это значение в исходное уравнение: .

Пример. Решить уравнение .

Метод Бернулли. Полагаем и .

Тогда .

1) , , , .

2) , т.е. , .

Итак, .

Метод Лагранжа. Решаем уравнение .

Имеем . Заменяем с на с(х): .

Тогда .

Подставляем . Получаем .

Пример. Решить уравнение .

Учитывая, что , то от исходного уравнения переходим к линейному уравнению . Применим подстановку . Получаем . Находим .

Находим .

Получаем .

1.7. Уравнение Бернулли

Уравнения вида , где - функции от х, которые предполагаются определенными и непрерывными в интервале ; n – вещественное число, отличное от 0 и 1, называются уравнением Бернулли. Уравнение Бернулли приводится к линейному уравнению делением обеих его частей на и введение новой искомой функции z по формуле .

Пример. Решить уравнение .

Делим обе части уравнения на : . Заменим , тогда . Получаем – линейное уравнение. Решим методом Бернулли. Заменим , тогда .

.

1) .

2) .

Получаем .

1.8. Уравнения в полных дифференциалах

Дифференциальное выражение является полным дифференциалом, если существует такая функция u(x,y), полный дифференциал которой равен данному выражению: .

Теорема. Для того чтобы выражение было полным дифференциалом, необходимо и достаточно, чтобы выполнялось тождество:

.

Если левая часть уравнения является полным дифференциалом некоторой функции u(x,y), то это уравнение называется уравнением в полных дифференциалах.

Таким образом, имеем равенство , которое означает, что между переменными х и у существует зависимость вида , где С – произвольная постоянная. Функция определяется по формуле .

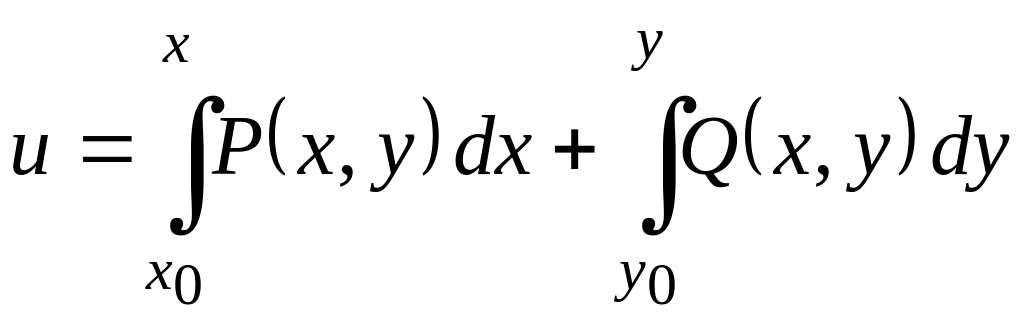Пример. Найти общий интеграл уравнения .

Проверим выполнение теоремы: Þ левая часть дифференциального уравнения есть полный дифференциал некоторой функции . Найдем ее: =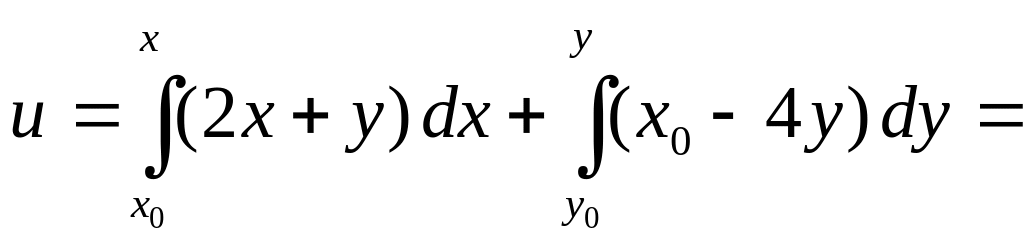

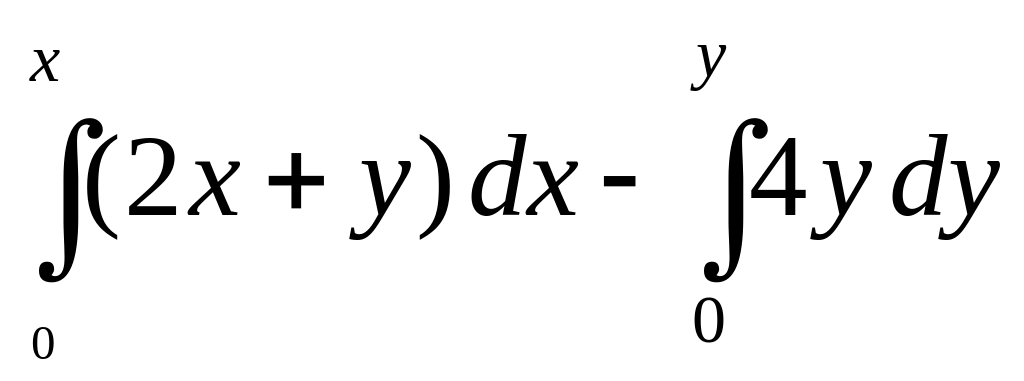. Так как C, получим .

Замечания

1. Если условие не выполняется, то дифференциальное уравнение не является уравнением в полных дифференциалах. Его приводят к уравнению в полных дифференциалах путем умножения его на некоторую функцию t(x;y), называемую интегрирующим множителем, где или .

2. Общий интеграл уравнения 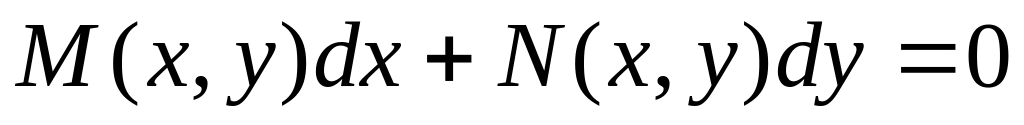в полных дифференциалах записывается в виде 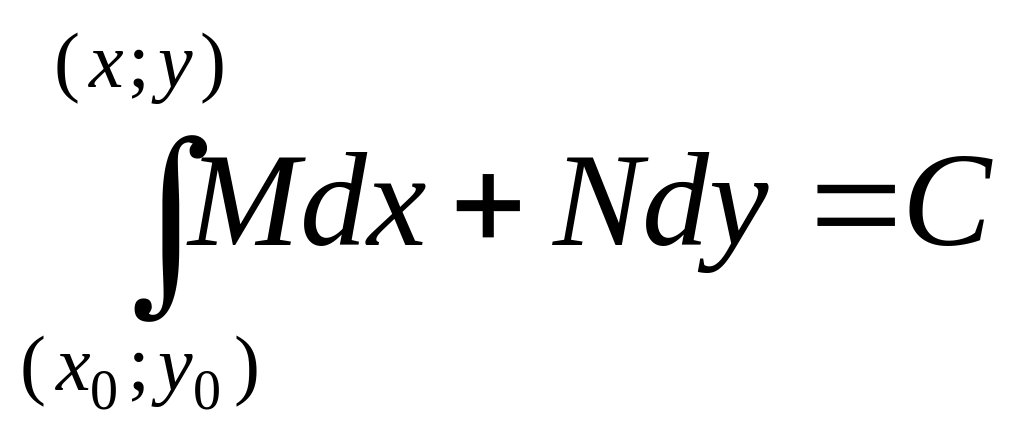, где левая часть есть криволинейный интеграл второго рода по любому пути, соединяющему фиксированную точку (х₀;у₀) с точкой (х; у).

Пример. Решить уравнение .

Здесь . Однако 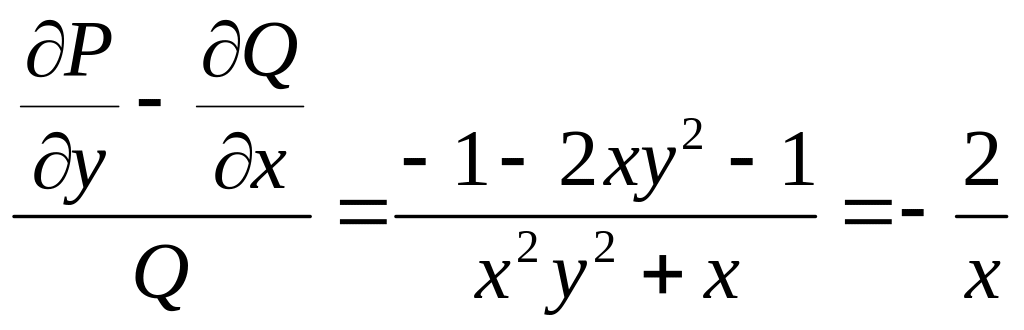. Таким образом, интегрирующий множитель зависит от х, имеем: . Умножаем исходное уравнение на , получаем: - это уравнение в полных дифференциалах. Решая уравнение, получим: .