§ 3. Площадь криволинейной трапеции

Определение. Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абсцисс и прямыми x=a, x=b, называется криволинейной трапецией.

Способы нахождения площади криволинейной трапеции

1. Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке [a;b], то площадь соответствующей криволинейной трапеции равна приращению первообразных. Дано: f(x)– непрерывная неопр. функция, x[a;b]. Доказать: S = F(b) – F(a), где F(x) – первообразная f(x).

Доказательство:

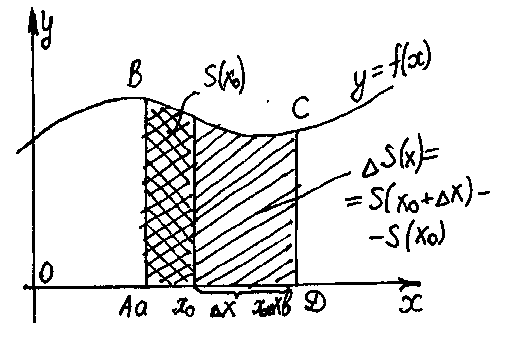
Рис 4

1) Рассмотрим вспомогательную функцию S(x). Каждому x[a;b] поставим в соответствие ту часть криволинейной трапеции (рис 4), которая лежит левее прямой, проходящей через точку с этой абсциссой и параллельно оси ординат.

Следовательно, S(a)=0 и S(b)=S_тр 2) Докажем, что S(a) – первообразная f(x).

1. D( f ) = D(S) = [a;b]

2. S’(x₀)= lim( S(x₀+x) – S(x₀) / x ), при x0 S – прямоугольник

3. при x0 со сторонами x и f(x₀)

S’(x₀) = lim(x f(x₀) /x) = lim f(x₀) = f(x₀): т.к. x0 точка,

^{x0 x0}

то S(x) – первообразная f(x).

Следовательно, по теореме об общем виде первообразной

S(x) = F(x) + C.

3. Т.к. S(a)=0, то S(a) = F(a)+C C = –Fa

4. S = S(b)=F(b)+C = F(b)–F(a)

II.

Рис 5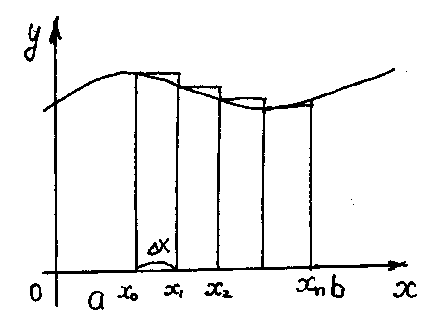

1). Разобьем отрезок [a;b] на n равных частей (рис 5). Шаг разбиения

x=(b–a)/n. При этом S_тр=lim(f(x₀)x+f(x₁)x+...+f(x_n))x=

^n

= lim x(f(x₀)+f(x₁)+...+f(x_n))

При n получим, что S_тр= x(f(x₀)+f(x₁)+...+f(x_n))Предел этой суммы называют определенным интегралом.

_b

S_тр= f(x)dx.

^a

Сумма, стоящая под пределом, называется интегральной суммой.

Определенный интеграл это предел интегральной суммы на отрезке [a;b] при n. Интегральная сумма получается как предел суммы произведений длины отрезка, полученного при разбиении области определения функции в какой либо точке этого интервала.

a — нижний предел интегрирования;

b — верхний предел интегрирования.[10]

§ 4. Площадь поверхности вращения

Пусть кривая АВ является графиком функции у = f(х) ≥ 0, где х [а;b], а функция у = f(х) и ее производная у' = f'(х) непрерывны на этом отрезке.

Найдем площадь S поверхности, образованной вращением кривой АВ вокруг оси Ох (рис 8).

Применим схему II (метод дифференциала).

1. Через произвольную точку х [а; b] проведем плос­кость П, перпендикулярную оси Ох. Плоскость П пере­секает поверхность вращения по окружности с радиусом у - f(х). Величина S поверхности части фи­гуры вращения, лежащей левее плоскости, является функ­цией от х, т. е. s = s(х) s(а) = 0 и s(b) = S).

2. Дадим аргументу х приращение Δх = dх. Через точку х + dх [а; b] также проведем плоскость, перпендику­лярную оси Ох. Функция s = s(х) получит приращение Δs, (изображенного на рис 6 в виде “пояска”).

Рис 6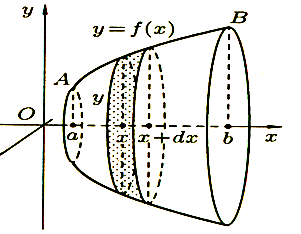

Найдем дифференциал площади ds, заменяя образо­ванную между сечениями фигуру усеченным конусом, об­разующая которого равна dl, а радиусы оснований рав­ны у и у + dу. Площадь его боковой поверхности равна ds = (у + у + dу) • d1 = 2 ydl + dydl. Отбрасывая произведение dу d1 как бесконечно малую высшего порядка, чем ds, получаем ds = 2 уdl, или, так как d1 = dx.

1. Интегрируя полученное равенство в пределах от х = а до х = b, получаем S 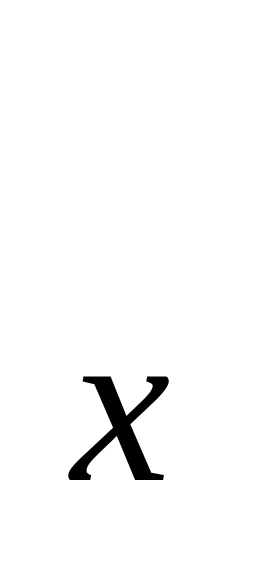= 2 y dx.

Если кривая AB задана параметрическими уравнениями x = x(t), y = y(t), t ≤ t ≤ t , то формула для площади поверхности вращения принимает вид

S = 2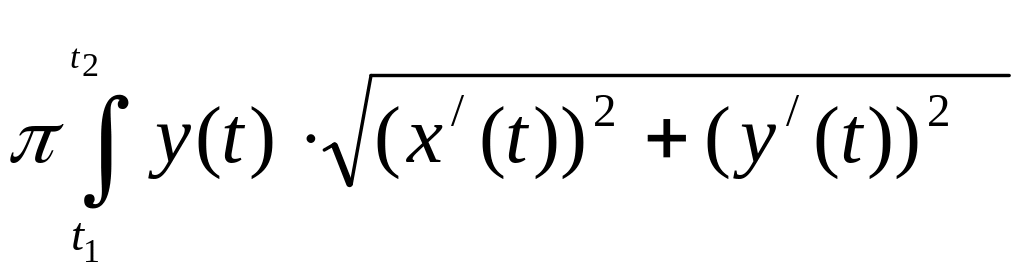 dt. [4]

Пример: Найти площадь поверхности шара радиуса R.

Решение: Можно считать, что поверхность шара образована вращением полуокружности y = , -R ≤ x ≤ R, вокруг оси Ox. По формуле S = 2 y dx находим

S = 2 =

[7]

Заключение. Наука прошла большой и сложный путь развития от самого элементарного к более сложному. Человечество прошло и проходит длительный путь от незнания к знанию, непрерывно заменяя на своем пути неполное и несовершенное знание все более полным и совершенным.

Интеграл - одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой - измерять площади, объемы, длины дуг, работу сил за определенный промежуток времени и т. п.

Строгое изложение теории интеграла появилось только в 19 веке. Решение этой задачи связано с именем О. Коши, одного из крупнейших математиков немецкого ученого Б. Римана и французского математика Г. Дарбу. Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены К. Жорданом.

Различные обобщения понятия интеграла в начале нашего столетия были предложены французскими математиками А. Лебегом и А. Данжуа, советским математиком А. Я. Хинчиным.

Интеграл используется в таких науках как физика, геометрия, математика и других науках. При помощи интеграла вычисляют работу силы, находят координаты центр масс, путь, пройденный материальной точкой. В геометрии интеграл используется для вычисления объема тела, нахождение длины дуги кривой.

Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности.

Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл - это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.

Литература

1. Виленкин М. Я., О. С. Ивашев – Мусатов, С. И. Шварцбурд, «Алгебра и математический анализ», Москва, 1993г.

2. Власов В. Г. «Конспект лекций по высшей математике». Москва Айрис 1997г.

3. Иванов А.А. «Курс лекций по математике».

4. Ильин В.А., Позняк Э.Г. «Основы математического анализа» часть I. Москва, 1982г.

5. Кальницкий Л.А «Специальный курс высшей математики для втузов», Москва,1976.

6. Колмогоров А. Н, А. М Абрамов и др. «Алгебра и начало математического анализа. Учебник для 10 – 11 кл.». – 17-е изд. – М.: Просвещение, 2008 г.

7. Кузнецов Д.А. «Сборник задач по высшей математики» Москва, 1983 г.

8. Никольский С. Н. «Элементы математического анализа». – М.: Наука, 1981г.

9. Понтрягин Л. Н. «Математический анализ для школьников». – 2-е изд., перераб. – М.: Наука, 1983г.

10. Фихтенгольц Г. М «Курс дифференциального исчисления. Том 2».

10