0. 2.4. Щільність розподілу імовірностей

Якщо функція абсолютно неперервна, тобто диференційована при всіх , то її похідна

називається щільністю розподілу імовірностей неперервної випадкової величини.

Розглянемо основні властивості щільності розподілу імовірностей.

1. Функція невід’ємна, тобто 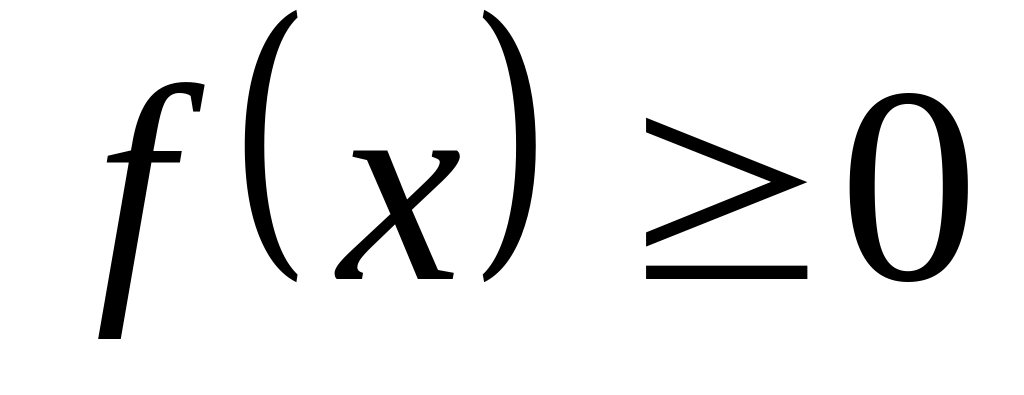при всіх . Це є наслідком того, що функція - неспадна.

2. Функція задовольняє умові норміровки

.

3. Якщо задано щільність розподілу імовірностей , то шляхом інтегрування можна знайти функцію розподілу:

.

4. Для будь-яких

.

Інколи, особливо в літературі технічного спрямування, називають інтегральною функцією розподілу імовірностей, а - диференціальною функцією розподілу імовірностей випадкової величини.

Значення функції не є імовірностями подій (це щільність) і тому можуть бути більшими 1. Вони мають фізичну розмірність, обернену розмірності, яка відноситься до значень самої випадкової величини. Наприклад, якщо розмірність випадкової величини [Вольти], то розмірність - .

На рис. 2.5 наведено приклад щільності розподілу імовірностей деякої випадкової

Рис. 2.5. Щільність розподілу імовірностей

величини. Згідно з властивістю норміровки, площа між кривою і віссю абсцис дорівнює 1. Імовірність того, що випадкова величина набуде значення, яке розташоване в межах інтервалу , дорівнює площі, заштрихованій на рисункові.

Значення випадкової величини , при якому набуває максимального значення, називається модою. На рис. 2.5 . Криві щільності можуть бути унімодальними, як на рис. 2.5, або полі модальними, які мають декілька максимумів (не обов’язково одинакових).

0. 2.5. Векторні випадкові величини

Розглянутий раніше теоретико-імовірнісний опис випадкових величин можна узагальнити на довільну сукупність випадкових величин: . Цю сукупність можна розглядати як випадковий вектор або випадкову точку у -вимірному евклідовому просторі з випадковими декартовими координатами .

Приклад 2.4. Нехай маємо деяку інформаційну систему (ІС) з виходами (рис. 2.6). Розглянемо значення напруги у фіксований момент часу на кожному із виходів.

Рис. 2.6. Приклад векторної випадкової величини

Тоді можливі значення напруги у момент часу на першому виході будуть зображати собою значення випадкової величини . На другому виході – значення випадкової величини . І так далі. В цілому, можливі значення напруги на всіх виходах і будуть зображати собою значення векторної випадкової величини .

Аналогічно, як і для одновимірної випадкової величини, вводиться багатовимірна функція сумісного розподілу імовірностей векторної випадкової величини.

,

тобто, за означенням, функція дорівнює імовірності події, яка полягає в тому, що випадкова величина не перевищує значення і випадкова величина не перевищує значення і т.д. до випадкової величини включно, тобто йде мова про перетин подій .

Сумісна функція розподілу неперервна зліва і неспадна по кожній змінній .

Окрім того багатовимірна сумісна функція розподілу має такі властивості:

1. , де може дорівнювати будь-якому значенню із сукупності індексів .

2. .

3. Багатовимірна сумісна функція розподілу є симетричною функцією відносно своїх аргументів , тобто

,

де - будь-яка перестановка індексів .

3. Функція розподілу задовольняє умові узгодженості, тобто

, (2.3)

де . Отже із розподілу більшої розмірності завжди можна отримати так званий маргінальний розподіл меншої розмірності за формулою (2.3). Обернене твердження у загальному випадку не вірне. Воно буде вірним лише для незалежних у сукупності випадкових величин . У цьому випадку

.

Змішана похідна -го порядку (якщо вона існує) функції розподілу від змінних

називається -вимірною сумісною щільністю розподілу імовірностей векторної випадкової величини .

Основні властивості -вимірною сумісною щільністю розподілу імовірностей наступні.

1. Вона є невід’ємною функцією

.

2. Багатовимірна сумісна щільність розподілу імовірностей, як і одновимірна, задовольняє умові нормування. Тобто

.

3. Якщо відома багатовимірна сумісна щільність розподілу імовірностей , то відповідна сумісна функція розподілу векторної випадкової величини знаходиться за формулою

.

4. На основі сумісної щільності розподілу імовірностей більшої розмірності завжди можна знайти сумісну щільність розподілу меншої розмірності, тобто

.

5. Для незалежних у сукупності випадкових величин

.

6. Імовірність того, що випадковий вектор в результаті експерименту набуде значення (у вигляді -вимірного вектора), яке міститься у -вимірному кубі: , знаходиться за формулою:

.

Для ілюстрації розглянемо рис. 2.7 з двовимірною щільністю розподілу

імовірностей . Імовірність попадання двовимірного випадкового вектора

Рис. 2.7. Двовимірна сумісна щільність розподілу імовірностей

випадкового вектора

в заштрихований на рисунку прямокутник дорівнює чисельно об’ємові шестигранної фігури і може бути обчислена за формулою

.