
- •Випадкові події. Імовірність
- •Випадкові події
- •Умовні ймовірності
- •Випадкові величини і їх статистичні характеристики
- •Означення випадкової величини. Класифікація
- •2.2. Розподіл імовірностей дискретної випадкової величини
- •2.3. Функція розподілу імовірностей випадкової величини
- •2.4. Щільність розподілу імовірностей
- •2.5. Векторні випадкові величини
- •2.6. Числові характеристики випадкових величин
Умовні ймовірності
Почнемо розгляд цього питання з прикладу, використовуючи лапласівське означення імовірностей, тобто будемо виходити із моделі з рівно ймовірними (рівно можливими) елементарними наслідками ( див. у п. 1.2. класичне означення імовірності).
Приклад 1.6. Розглянемо
однократне підкидання грального кубика.
Тут
![]() ,
де
,
де
![]() - кількість очок на верхній грані
- кількість очок на верхній грані
![]() ,
,
![]() Розглянемо події:
Розглянемо події:
![]() - випало два очка;
- випало два очка;
![]() -
випала парна кількість очок. Імовірність
цих подій, згідно з класичним означенням
імовірності,
-
випала парна кількість очок. Імовірність
цих подій, згідно з класичним означенням
імовірності,
![]()
![]() .
Нехай в результаті однократного
підкидання кубика виникла подія
.
Тоді можна розглянути подію
.
Нехай в результаті однократного
підкидання кубика виникла подія
.
Тоді можна розглянути подію
![]() - випадання двох очок за умови, що випала
парна кількість очок. Очевидно імовірність
цієї події
- випадання двох очок за умови, що випала
парна кількість очок. Очевидно імовірність
цієї події
![]() .∙
.∙
Таким чином ми приходимо до
поняття умовної події
і умовної імовірності
![]() .
.
Зупинимось на більш строгих
означеннях співвідношень для умовних
імовірностей. Якщо розглядається
імовірність події
за умови, що виникла подія
,
то така імовірність називається умовною
і позначається символом
.
При означенні умовної імовірності
первинний (визначений для експерименту,
здійснення якого привело до появи події
)
простір елементарних подій
після виникнення події
переходить (звужується) до простору
елементарних подій
![]() і складається з тих елементарних подій
і складається з тих елементарних подій
![]() де
де
![]() - кількість елементарних подій, із яких
складається подія
,
при появі яких виникає подія
.
- кількість елементарних подій, із яких
складається подія
,
при появі яких виникає подія
.
Якщо звернутись до прикладу
1.6, з якого ми починали даний підрозділ,
то
![]() .
.
Означення 1.1.
Умовною імовірністю події
за умови події
з
![]() називається величина
називається величина
![]() .
.
Ми приходимо до нового (звуженого) імовірнісного простору:
![]() F
,
F
,
![]() ,
,
де присутні всі три елементи імовірнісного простору:
![]() - простір елементарних подій;
- простір елементарних подій;
![]() F
- система (алгебра)
подій;
F
- система (алгебра)
подій;
![]() - імовірність (умовна).
- імовірність (умовна).
Із означення умовної імовірності
випливає формула
![]() :
:
![]() ,
(1.3)
,
(1.3)
яка носить назву формули множення імовірностей.
Аналогічно можна ввести
умовну імовірність
![]()
![]()
і тоді формула множення імовірностей набуде виду
![]() .
(1.4)
.
(1.4)
Обидві формули рівнозначні.
Властивості умовних імовірностей:
1.
![]()
2.
![]() якщо
якщо
![]()
3.
![]()
4.
![]()
Зокрема, із властивостей 2 і 4 випливає
5.
![]()
Означення 1.2. Подія незалежна від події , якщо має місце рівність
![]()
Якщо подія
незалежна від події
,
то і подія
є незалежною від події
,
тобто
![]()
Для незалежних подій формули множення імовірностей (1.3) і (1.4) набувають такого виду:
![]() .
(1.5)
.
(1.5)
Приклад 1.7. Незалежними є похибки в двох вимірюваннях, виконаних різними спостерігачами різними приладами.∙
Означення
1.3. Події
![]() називаються незалежними
у сукупності, якщо для
будь-якої події
називаються незалежними
у сукупності, якщо для
будь-якої події
![]() із їх числа і довільних
із їх числа і довільних
![]() із їх числа події
і
із їх числа події
і
![]() взаємно
незалежні.
взаємно
незалежні.
Це означення еквівалентно наступному
![]()
для усіх
![]() .
.
Із означення 1.3 випливає
узагальнення формули множення імовірностей
(1.5) для незалежних у сукупності
![]() подій
подій
![]() :
:
![]() .
.
Можна також отримати узагальнення формул множення імовірностей (1.3) і (1.4) на випадок залежних подій
![]() .
.
В багатьох реальних ситуаціях
та чи інша подія
може з’явитися лише як випадковий
наслідок однієї із
несумісних подій
![]() ,
які складають повну групу подій і
називаються гіпотезами.
Зауважимо, що термін „випадковий
наслідок” означає, що кожна із гіпотез
може призвести до появи не тільки події
,
але і деяких інших подій
,
які складають повну групу подій і
називаються гіпотезами.
Зауважимо, що термін „випадковий
наслідок” означає, що кожна із гіпотез
може призвести до появи не тільки події
,
але і деяких інших подій
![]() (див. рис. 1.3).
(див. рис. 1.3).
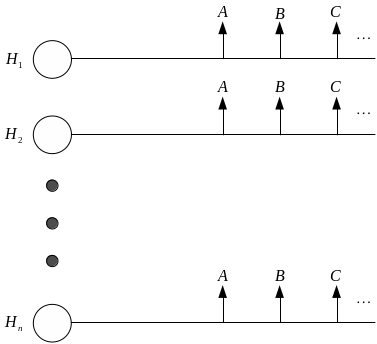
Рис. 1.3. Умовне графічне зображення схеми гіпотез
Приклад 1.8.
Маємо три урни, в
кожній з яких містяться червоні, чорні
та білі кульки. Вибирається навмання
одна із урн і виймається із неї одна
кулька. В цьому експерименті маємо три
гіпотези (![]() ):
):
![]() - вибір першої урни;
- вибір першої урни;
![]() - вибір другої урни;
- вибір другої урни;
![]() - вибір третьої урни. При виборі однієї
із урн (гіпотез) і вийманні потім однієї
кульки можуть виникнути такі несумісні
події:
- колір кульки червоний;
- колір кульки чорний;
- колір кульки білий.
- вибір третьої урни. При виборі однієї
із урн (гіпотез) і вийманні потім однієї
кульки можуть виникнути такі несумісні
події:
- колір кульки червоний;
- колір кульки чорний;
- колір кульки білий.
В
схемі гіпотез робиться припущення, що
відомі імовірності гіпотез
![]() і відомі умовні імовірності події
для кожної з гіпотез:
і відомі умовні імовірності події
для кожної з гіпотез:
![]() .
Ставиться задача: визначити
безумовну імовірність
події
,
при обчисленні якої приймаються до
уваги всі випадки (гіпотези),
наслідком яких може бути подія
.
Аналогічним чином може
ставитись задача і відносно подій
.
Ставиться задача: визначити
безумовну імовірність
події
,
при обчисленні якої приймаються до
уваги всі випадки (гіпотези),
наслідком яких може бути подія
.
Аналогічним чином може
ставитись задача і відносно подій
![]() і
т.д.
і
т.д.
Приклад
1.9. Якщо звернутися до
прикладу 1.8 і вважати що шанси вибору
кожної із урн рівноцінні, то імовірності
гіпотез
![]() .
Умовні ж імовірності подій
.
Умовні ж імовірності подій
![]() і
залежать від кількості кульок у кожній
із урн і їх розподілу за кольорам.
Наприклад, якщо в першій урні всього
кульок 10 і з них 5 – червоних, 1 – чорна
і 4 – білих, то
і
залежать від кількості кульок у кожній
із урн і їх розподілу за кольорам.
Наприклад, якщо в першій урні всього
кульок 10 і з них 5 – червоних, 1 – чорна
і 4 – білих, то
![]() .
.
Відзначимо, що подія
тоді
і лише тоді, коли виникає одна із подій
![]() ,
причому, ці події несумісні, так же само
як і гіпотези
.
Тому, згідно з правилом складання
імовірностей несумісних подій (див.
аксіому 3)
,
причому, ці події несумісні, так же само
як і гіпотези
.
Тому, згідно з правилом складання
імовірностей несумісних подій (див.
аксіому 3)
![]() .
(1.6)
.
(1.6)
Застосовуючи теорему множення імовірностей (1.3), отримаємо
![]() .
(1.7)
.
(1.7)
Підставляючи тепер (1.7) в (1.6), знаходимо безумовну ймовірність події
![]() .
.
Остання формула в літературі отримала назву формули повної імовірності.
В цій же схемі гіпотез можна
ставити і розв’язувати
і таку задачу. Нехай здійснено випробування
і виникла подія
.
Ставиться запитання: з якою із гіпотез
слід пов’язати появу події
![]() У зв’язку з тим, що викладена ситуація
є імовірнісною, то і відповідь на
поставлене запитання може бути лише
імовірнісною а не детерміністичною.
Для вирішення поставленої задачі
потрібно обчислити умовну імовірність
кожної із гіпотез за умови настання
події
:
У зв’язку з тим, що викладена ситуація
є імовірнісною, то і відповідь на
поставлене запитання може бути лише
імовірнісною а не детерміністичною.
Для вирішення поставленої задачі
потрібно обчислити умовну імовірність
кожної із гіпотез за умови настання
події
:
![]() .
Віддається перевага тій із гіпотез, для
якої буде найбільшою знайдена умовна
імовірність. Як же знайти
.
Віддається перевага тій із гіпотез, для
якої буде найбільшою знайдена умовна
імовірність. Як же знайти
![]()
На основі формул множення
імовірностей (1.3) і (1.4) для імовірності
сумісної появи події
і гіпотези
![]() маємо
маємо
![]() .
(1.8)
.
(1.8)
Беручи до уваги праву рівність в (1.8), запишемо
![]() .
.
Але за формулою повної імовірності
![]() .
.
Отже

Останнє співвідношення отримало в літературі назву формули оберненої імовірності або формули Байєса.
